Разработка урока "Векторы в пространстве"

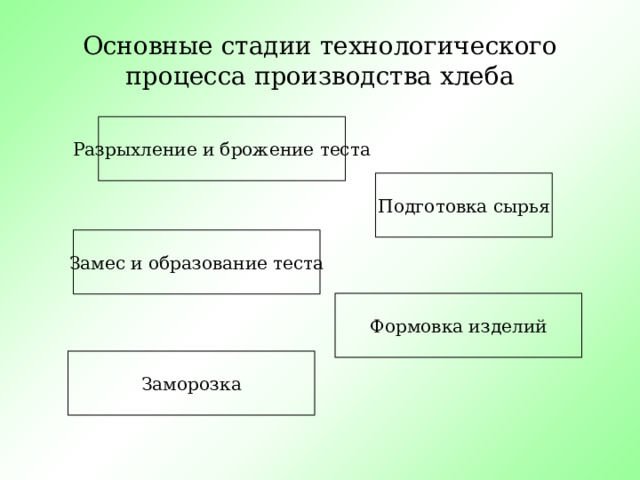
Основные стадии технологического процесса производства хлеба

Разрыхление и брожение теста

Подготовка сырья

Замес и образование теста

Формовка изделий

Заморозка

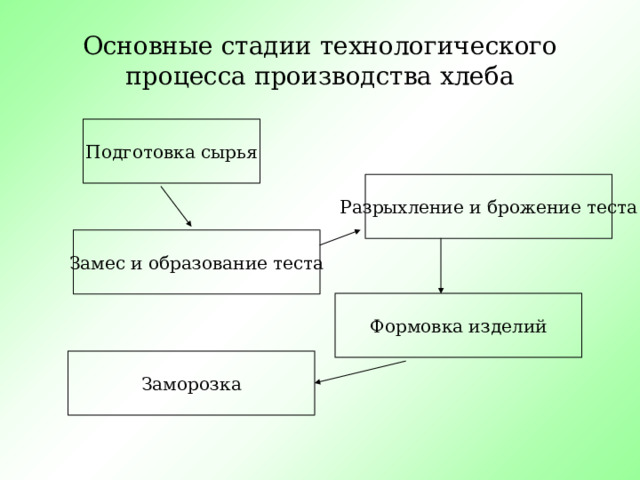
Основные стадии технологического процесса производства хлеба

Подготовка сырья

Разрыхление и брожение теста

Замес и образование теста

Формовка изделий

Заморозка

Тема урока:

Векторы в пространстве

Цели урока

• Изучить определение вектора в пространстве и связанные с ним понятия.

• Закрепить знания решением задач .

Задание

Записать все термины по теме «Векторы на плоскости».

Термины по теме «Векторы на плоскости».

Вектор

Нулевой вектор

Длина вектора

Коллинеарные векторы

Сонаправленные векторы

Противоположно направленные векторы

Равные векторы

Повар   вектор  -  это  профессионал своего дела, специализирующийся на приготовлении и представлении блюд. Сочетая в себе творческий подход и навыки рациональной организации рабочего процесса,  повар   вектор  способен создать уникальные кулинарные шедевры, учитывая требования клиента и последние тенденции в мире гастрономии.

Вектор развития личности

Вектор развития веб -сайта

Вектор развития мобильных приложений

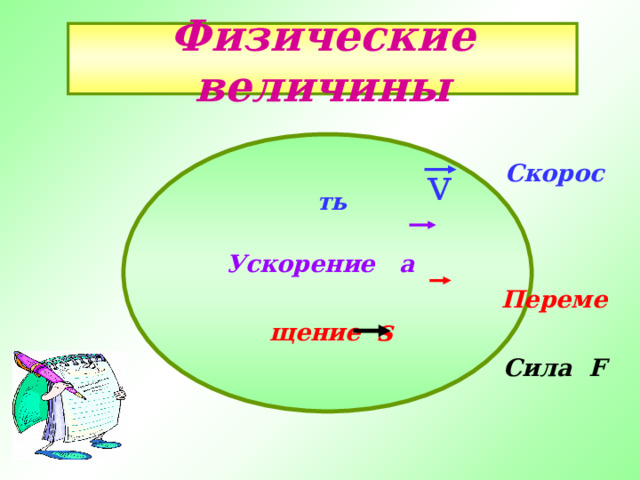
Физические величины

v

Скорость

Ускорение а

Перемещение s

Сила F

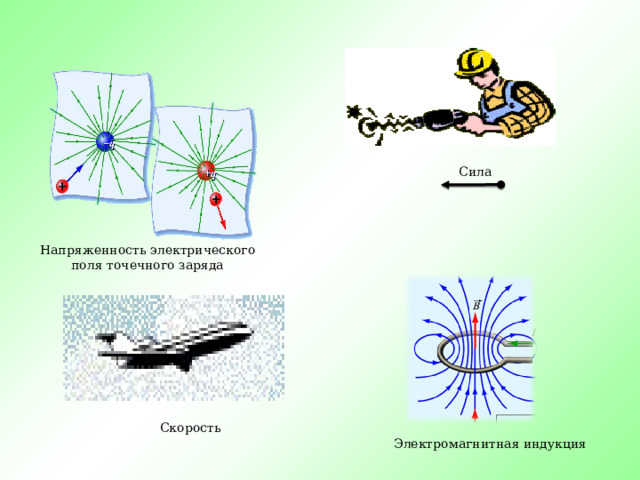
Сила

Напряженность электрического поля точечного заряда

Скорость

Электромагнитная индукция

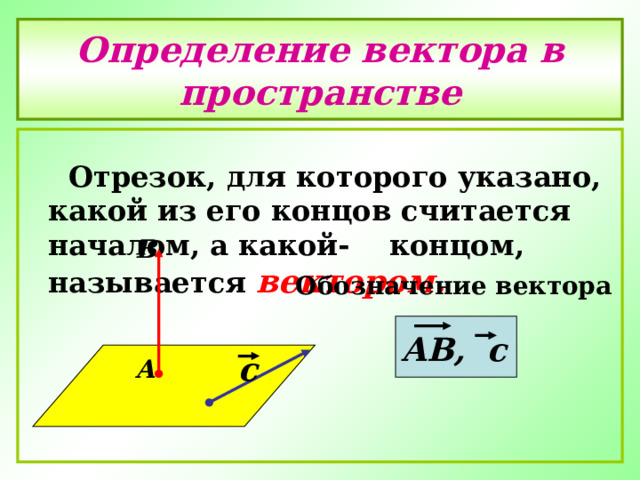
Определение вектора в пространстве

Отрезок, для которого указано, какой из его концов считается началом, а какой- концом, называется вектором .

В

Обозначение вектора

АВ, с

с

А

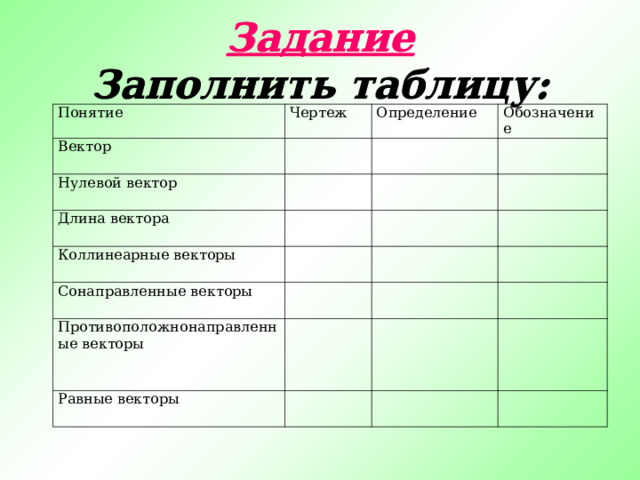
Задание Заполнить таблицу:

Задание Заполнить таблицу:

Понятие

Чертеж

Вектор

Определение

Нулевой вектор

Обозначение

Длина вектора

Коллинеарные векторы

Сонаправленные векторы

Противоположнонаправленные векторы

Равные векторы

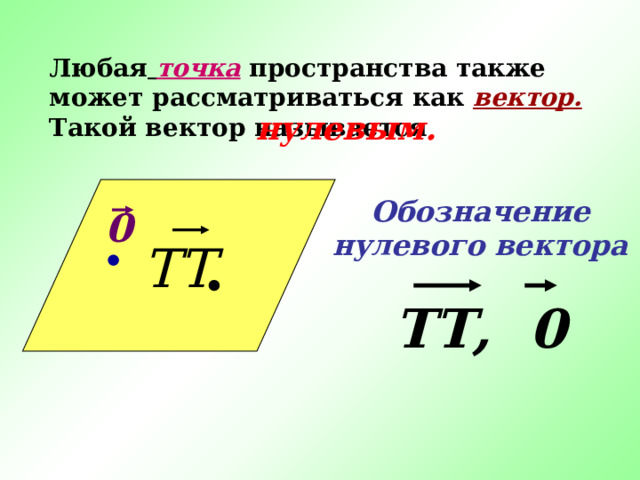
Любая точка пространства также может рассматриваться как вектор. Такой вектор называется

нулевым.

ТТ

Обозначение нулевого вектора

ТТ, 0

0

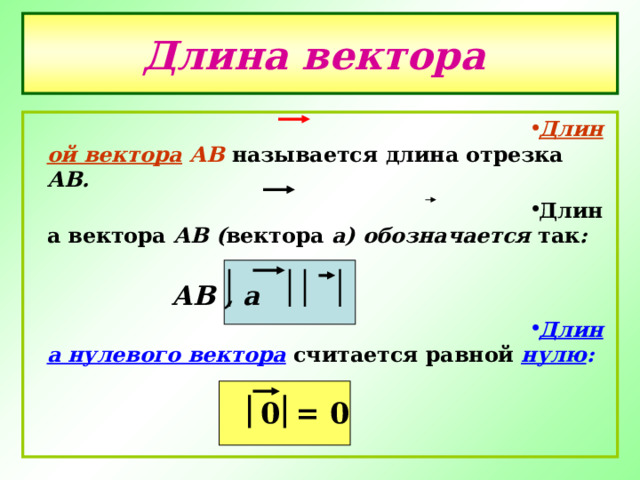
Длина вектора

• Длиной вектора АВ называется длина отрезка АВ.

• Длина вектора АВ ( вектора а) обозначается так :

АВ , а

• Длина нулевого вектора считается равной нулю :

= 0

0

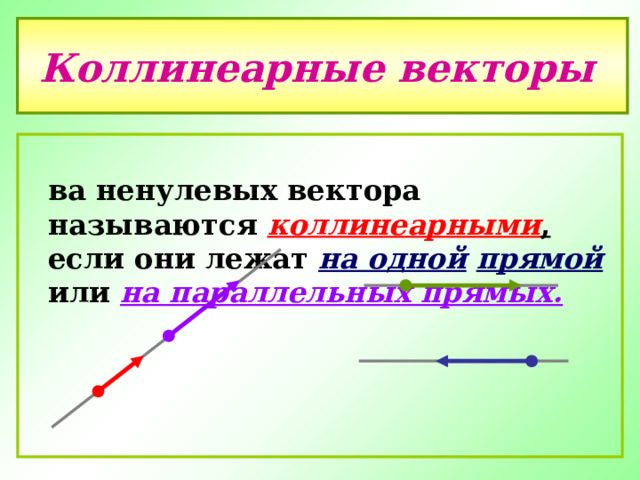
Коллинеарные векторы

• Два ненулевых вектора называются коллинеарными , если они лежат на одной прямой или на параллельных прямых.

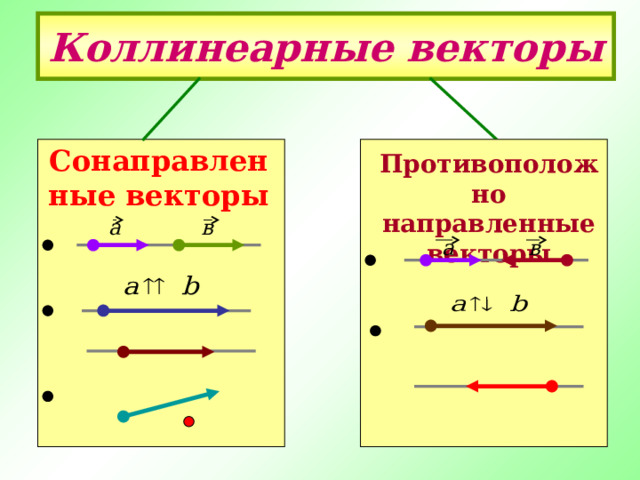
Коллинеарные векторы

Сонаправленные векторы

Противоположно направленные векторы

в

а

а

в

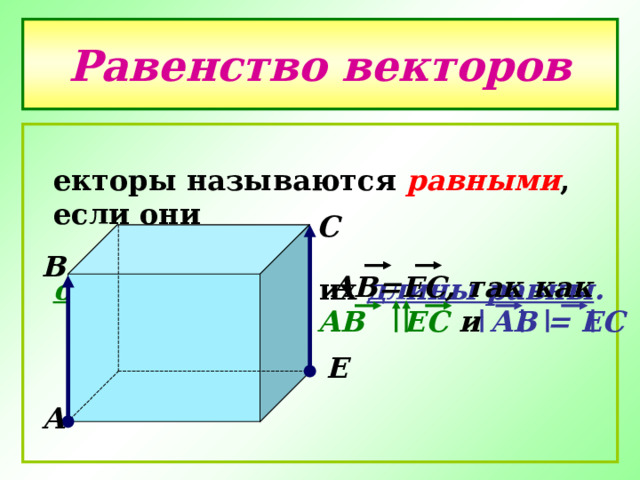
Равенство векторов

Векторы называются равными , если они

сонаправлены и их длины равны .

С

В

АВ=ЕС, так как

АВ ЕС и АВ = ЕС

Е

А

Понятие вектора появилось в 19 веке в работах математиков Г. Грассмана У. Гамильтона

Современная символика для обозначения вектора r была введена в 1853 году французским математиком О. Коши .

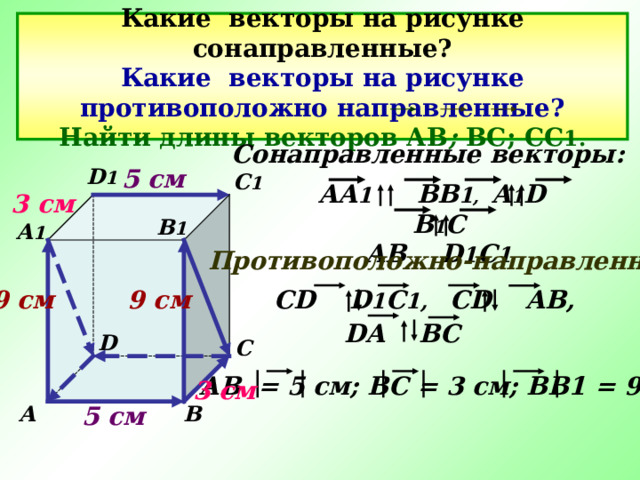
Какие векторы на рисунке сонаправленные? Какие векторы на рисунке противоположно направленные? Найти длины векторов АВ ; ВС; СС 1.

Сонаправленные векторы:

5 см

D 1

C 1

AA 1 BB 1 , A 1 D B 1 C

AB D 1 C 1

3 см

В 1

A 1

Противоположно-направленные:

CD D 1 C 1, CD AB,

DA BC

9 см

9 см

D

C

АВ = 5 см; ВС = 3 см; ВВ1 = 9 см.

3 см

A

B

5 см

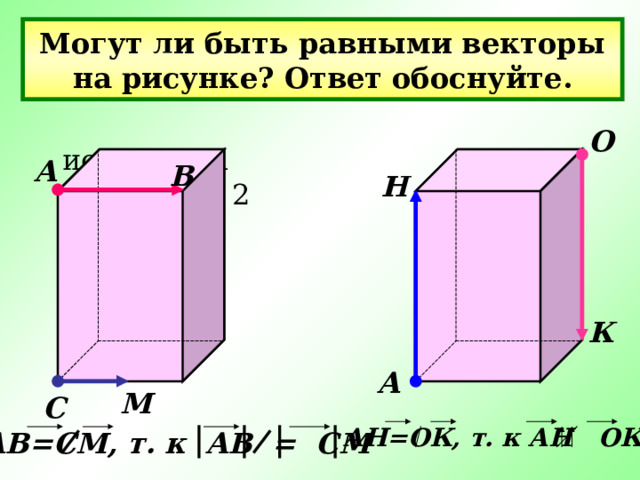
Могут ли быть равными векторы на рисунке? Ответ обоснуйте.

• Рисунок № 1 Рисунок № 2

О

А

В

Н

К

А

М

С

АН=ОК, т. к АН ОК

АВ=СМ, т. к АВ = СМ

1) Фамилия математика, в работе которого впервые появилось понятие вектора. 2) Как называется отрезок, для которого указано начало, конец и направление? 3) Название двух ненулевых векторов, лежащих на одной прямой или на двух параллельных прямых. 4) Математик, который ввел современное обозначение вектора. 5) Как называется расстояние между точками А и В у вектора АВ? 6) Как называются два вектора, если они сонаправлены, и их длины равны?

7) Векторная величина в физике.

Кроссворд

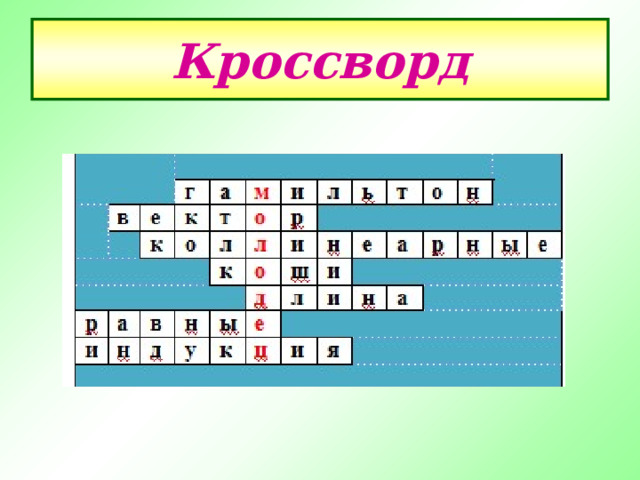
Кроссворд

В

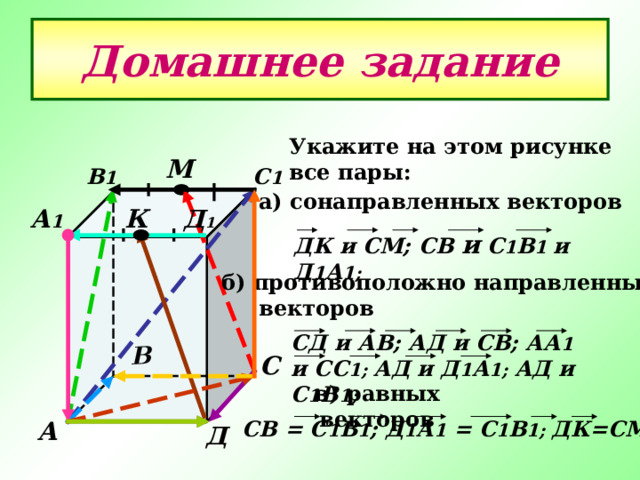
Домашнее задание

Укажите на этом рисунке

все пары:

М

С 1

В 1

а) сонаправленных векторов

А 1

К

Д 1

ДК и СМ; C В и С 1 В 1 и Д 1 А 1;

б) противоположно направленных

векторов

СД и АВ; АД и СВ; АА 1 и СС 1; АД и Д 1 А 1; АД и С 1 В 1;

С

в) равных векторов

А

C В = С 1 В 1 ; Д 1 А 1 = С 1 В 1; ДК=СМ

Д

Тема урока: Векторы в пространстве

Цели урока:

• Изучить определение вектора в пространстве и связанные с ним понятия.
• Закрепить знания решением задач .

Спасибо за урок!