Цели и задачи урока:
Образовательные: вывести правило вычитания чисел с разными знаками и рассмотреть применение этого правила при решении примеров, задач и уравнений, совершенствовать вычислительные навыки;
Развивающие: способствовать развитию умения наблюдать, сравнивать, анализировать, использовать установленные ранее факты для обоснования новых фактов и для решения конкретных задач, совершенствовать устную математическую речь; развивать творческие способности через активные формы деятельности.
Воспитательные: способствовать формированию таких качеств личности как познавательная активность, любознательность, внимательность, критичность, организованность, самостоятельность, умение слушать мнение других.
Тип урока: урок "открытия" нового знания.
Методы обучения: проблемный, частично – поисковый.
Формы организации познавательной деятельности учащихся: фронтальная работа с классом, парная работа, индивидуальная работа, групповая работа.
Материально техническая база: компьютер, мультимедийный проектор, экран.
"Знание только тогда знание, когда оно приобретено усилиями своей мысли, а не памятью"
Л. Н. Толстой
Ход урока
1. Организация начала занятия.
Подготовка учащихся к работе на занятии. Приветствие учителя( слайд 1)
Если разобраться - всё возможно
Испытать, достигнуть и понять.
В этом мире всё совсем не сложно,
Если самому не усложнять.
2. Мотивация урока.
Эпиграфом к нашему уроку будут слова "Мир освещается солнцем, а человек — знанием" (слайд 2)
3. Актуализация опорных знаний. Проверка домашнего задания.
"Для того чтобы усовершенствовать ум, надо больше размышлять, чем заучивать" Р. Декарт
1. Обучающимся предлагается вспомнить пословицы, поговорки в которых встречаются слова ученье, знание (слайд 3)
Век живи - . . . ; Знание —. . . ; Ученье — свет, а не ученье - . . . ;
На ошибках. . . ; Повторенье —. . .
2. Учащимся предстоит выполнить следующие задания

( учащиеся обмениваются тетрадями и оценивают правильность решения заданий 2); 3) своего одноклассника, и результат записывается в лист самооценки).
4. Историческая справка (слайды7 - 8)
История возникновения отрицательных чисел очень давняя и долгая. Так как отрицательные числа являются чем - то ненастоящим, люди долгое время не признавали их существования.
Все началось в Китае, примерно во II веке до н. э. Возможно, в Китае их знали и раньше, но первое упоминание относится именно к тому времени. Там стали применять отрицательные числа и считали их «долгами», при этом положительные называли «имуществом». Той записи, которая существует сейчас, тогда не было, и отрицательные числа записывали черным цветом, а положительные красным.
Первое упоминание отрицательных чисел мы находим в книге «Математика в девяти главах» китайского ученого Чжан Цань.
Далее, в V - VI веках отрицательные числа стали использоваться достаточно широко в Китае и Индии. Правда, в Китае к ним, все - таки относились осторожно, старались их применение свести к минимуму, а в Индии, напротив, они использовались очень широко. Там с ними производились вычисления и отрицательные числа не казались чем - то непонятным.
Известные индийские ученые Брахмагупта и Бхаскара в своих учениях оставили подробные объяснения работе с отрицательными числами.
А в Древности, например, в Вавилоне и в Древнем Египте, отрицательные числа не использовали вовсе. А если при вычислении получалось отрицательное число, считалось, что решения нет.
Так и в Европе отрицательные числа не признавали очень долго. Их считали «мнимыми» и «абсурдными». Никаких действий с ними не совершали, а просто отбрасывали, если ответ получался отрицательным. Считали, что, если из 0 вычесть любое число, то ответом будет 0, так как ничто не может быть меньше нуля — пустоты.
Впервые в Европе свое внимание на отрицательные числа обратил Леонардо Пизанский (Фибоначчи). И описал их в своем произведении «Книга Абака» в 1202 году.
Позже, в 1544 году Михаил Штифель в книге «Полная арифметика» впервые ввел понятие отрицательных чисел и подробно описал действия с ними. «Нуль находится между абсурдными и истинными числами».
А в XVII веке математик Рене Декарт предложил откладывать отрицательные числа на цифровой оси слева от нуля.
С этого времени отрицательные числа стали повсеместно использовать и признавать, хотя еще долгое время многие ученые отрицали их.
В 1831 году Гаусс называл отрицательные числа абсолютно равнозначными с положительными. А то, что не все действия с ними можно совершать не считал чем - то страшным, с дробями, например, тоже не все действия можно делать.
А в XIX веке Уильман Гамильтон и Герман Грассман создали полную законченную теорию отрицательных чисел. С этого времени отрицательные числа обрели свои права и сейчас уже никто не сомневается в их реальности
5. Целеполагание (слайды 9 - 10)
Индийский математик Брахмагупта излагал свои правила так.
Сумма двух имуществ есть имущество;
Сумма двух долгов есть долг;
Сумма имущества и долга равна их разности.
Вопрос учащимся: Ребята, как вы понимаете эти правила? (обучающиеся высказывают свое мнение сопровождая конкретными примерами).
Весь материал – смотрите документ.

 Получите свидетельство
Получите свидетельство Вход
Вход



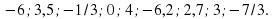
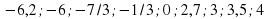 ( учащиеся оценивают правильность своего решения и результат записывают в лист самооценки).
( учащиеся оценивают правильность своего решения и результат записывают в лист самооценки).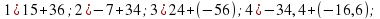
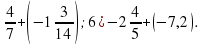
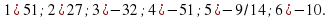
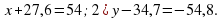


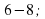
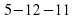 (убытки превосходят прибыль).
(убытки превосходят прибыль).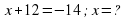
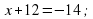
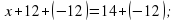
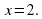
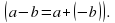
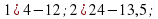
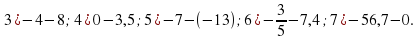
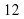
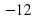
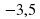
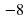
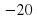










 Разработка урока по математике "Вычитание чисел с разными знаками" (79.75 КB)
Разработка урока по математике "Вычитание чисел с разными знаками" (79.75 КB)
 0
0 1183
1183 70
70 Нравится
0
Нравится
0


