Цель урока:
- расширить круг геометрических задач, решаемых с помощью теоремы Пифагора;
- познакомить учащихся с историей теоремы, этапами жизни и деятельности Пифагора Самосского;
- сформулировать и доказать теорему Пифагора.
- осуществить межпредметные связи геометрии с алгеброй, литературой;
- развитие воображения, логического мышления, познавательной активности;
- формирование умения самостоятельной работы.
План:
1. Практическая работа.
2. Историческая справка.
3. Жизнь и деятельность Пифагора.
4. Работа над теоремой.
5. Применение теоремы Пифагора.
6. Исследовательская работа.
7. Закрепление.
8. Домашнее задание.
9. Итоги урока.
1) Практическая работа.
1. Измерьте длину гипотенузы и катетов:
АВ=
АС=
ВС=
2. Найдите квадраты этих сторон:
АВ2=

АС2=
ВС2=
3. Какой вывод можно сделать?
2) Историческая справка.
Пифагор - древнегреческий учёный, 6 в. до н.э.
Древний Египет и Вавилон - египетский треугольник.
Настоящее время - более 100 доказательств.
3) Жизнь Пифагора Самосского.
Великий Пифагор родился около 570 г. до н.э. На острове Самосе. Отцом Пифагора был Мнессари, резчик по драгоценным камням.
По многим античным свидетельствам, мальчик был сказачно красив, в вскоре проявил и свои незаурядные способности.
Страть к музыке и поэзии Пифагор сохранил на всю жизнь. И, будучи признанным мудрецом, Пифагор начинал день с пения, он был великим философом и математиком.
4) Теорема Пифагора.
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Дано: ΔABC, <С = 90°
Доказать:
АВ2=АС2+ВС2
Доказательство:
ΔACDcosA=AD/AC
ΔABCccosA=AC/AB
AD/AC=AC/AB=AC2=AD*AB(1)
Рассматривая cos B, получаем: BC2=BD*AB(2)
Складывая (1) и (2), получаем: AC2+BC2=AD*AB+DB*AB=AB(AD+DB)=AB*AB=AB2
Весь материал - в документе.

 Получите свидетельство
Получите свидетельство Вход
Вход




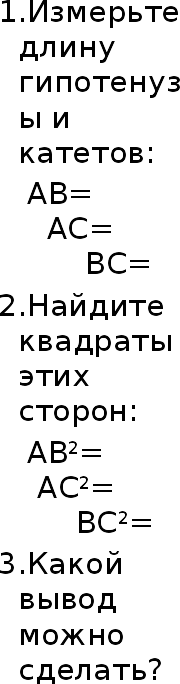




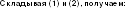
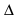 ABC
ABC

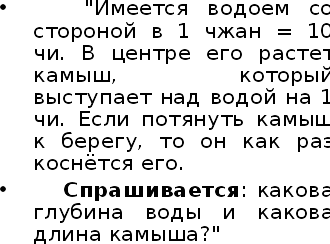











 Разработка урока по математике на тему "Теорема Пифагора" (0.14 MB)
Разработка урока по математике на тему "Теорема Пифагора" (0.14 MB)
 0
0 509
509 39
39 Нравится
0
Нравится
0




