Цели урока:
Обобщить и систематизировать знания и умения учащихся, связанные с решением логарифмических уравнений и систем.
формирование самостоятельности мышления, мыслительных операций: сравнение, анализ, синтез, обобщение, аналогия;
формирование таких качеств личности, как чёткость и организованность в работе;
умение контролировать свою деятельность, оценивать её, проявлять коллективизм и взаимопомощь.
Методический комментарий.
Этот урок является уроком обучающего повторения.
Основные этапы урока.
Организационный момент; постановка задачи, устная работа; самостоятельное решение логарифмических уравнений; решение систем уравнений; подведение итогов; выставление оценок; комментарии к домашнему заданию.
Организационный момент.
Ученикам предлагается листок с заданиями на урок и сообщается, каким образом будет организована работа на уроке.
Ход урока:
Устная работа
1. Теоретическая часть. Назвать свойства логарифмов (заполнить таблицу на доске или экране)

2.Найти значение выражения и прочитать фамилию известного математика, который изобрел логарифмы.
Непер. Джон Не́пер 1550—1617 — шотландский барон, математик, один из изобретателей логарифмов, первый публикатор логарифмических таблиц. «Я всегда старался, насколько позволяли мои силы и способности, освободить людей от трудности и скуки вычислений, докучливость которых обыкновенно отпугивает очень многих от изучения математики.»
Устные упражнения :
Определить верные равенства (найдите ошибки) :
Задание записано на доске либо экране.
1) log324 – log38 =16;
2) log315 + log33 = log35;
3) log553 = 2;
4) log2162 = 8.
5) 3log24 = log2 (4*3);
6) 3log23 = log227;
7) log327 = 4;
8) log223 = 8.
Вычислить:
а) log211 – log244
б) log1/64 + log1/69
в) 2 log 525 + 3 log 264
Результаты устной работы занести в таблицы (у каждого ученика на парте)
Осуществить взаимопроверку : 12 верных ответов – «5», 11 - «4», 8-10 – «3», 7 и менее – «2».
3. Повторение теоретического материала.
Назвать методы решения логарифмических уравнений.
Учащиеся называют, на доске или на экране появляется запись:
1. Преобразование логарифмических уравнений.
2. Замена переменных.
3. Потенцирование.
4. Логарифмирование.
5. Свойства монотонности.
2. Самостоятельная работа.
ЗАДАНИЯ:
Среди перечисленных уравнений выбрать и решить
а). те, которые решаются заменой переменных;
б). те, которые решаются логарифмированием
в). те, которые решаются с использованием свойств функции.
(а). заменой переменных №3 Ответ: 10, №7 Ответ:½; 1
б). логарифмированием №5 Ответ:1; 3 , №6 Ответ:1; ½; 16
в). с использованием свойств функции №8 Ответ:1.
г). преобразованием логарифмических уравнений № 1 Ответ:3, №2 Ответ:16, 3 №4 Ответ:-1; √2-1, №9 Ответ: Ответ:-1 )
Каждое задание выполняется на отдельном листочке и по мере решения сдаются учителю. Учащиеся, которые затрудняются в выборе уравнения или в его решении могут получить конвертики с пошаговыми подсказками . Уравнение, решенное правильно оценивается в 4 балла. Каждая подсказка минус 1 балл (у каждого уравнения по 3 подсказки, но можно использовать не все подсказки, а только одну или две)
У учащихся на столе табличка, которую заполняет учитель:
Перевод баллов в оценку;
От 32 - 36 баллов – оценка 5
От 25 - 31 баллов – оценка 4
От 15 - 19 баллов – оценка 3
Те учащиеся, которые выполнили задания раньше времени работают с дополнительными заданиями, для решения которых можно объединяться в группы по 4 человека.
ДОМАШНЕЕЕ ЗАДАНИЕ: дорешать не решенные уравнения; группы по дополнительному заданию готовят отчет (каждый член группы должен уметь объяснить решение системы); подобрать задания из вариантов ЕГЭ, связанных с логарифмическими уравнениями.
Весь материал – смотрите документ.

 Получите свидетельство
Получите свидетельство Вход
Вход



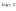
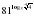
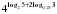









 Разработка урока математики "Решение логарифмических уравнений" (35.77 КB)
Разработка урока математики "Решение логарифмических уравнений" (35.77 КB)
 0
0 480
480 59
59 Нравится
0
Нравится
0


