Раздел: Геометрия. Тема: Правильные многогранники.

Презентация по математике:

«Правильные многогранники"

«Правильных многогранников вызывающе мало, но этот весьма скромный по численности отряд сумел пробраться в самые глубины различных наук» Л.Кэрролл

Название «правильные» идет от античных времен, когда стремились найти гармонию, правильность, совершенство в природе и человеке.

Контроль знаний:

• Сформулируйте понятие геометрии.

( Геометрия – наука о свойствах геометрических фигур ).

• Что такое планиметрия?

( Планиметрия – раздел геометрии, в котором изучаются свойства фигур на плоскости ).

• Что такое стереометрия?

( Стереометрия – раздел геометрии, в котором изучаются свойства фигур в пространстве ).

• Понятия геометрических фигур: Параллелограмм, окружность, квадрат, ромб.

Содержание учебного материала:

- Гексаэдр и его свойства.

- Тетраэдр и его свойства.

- Октаэдр и его свойства.

- Икосаэдр и его свойства.

- Додекаэдр и его свойства.

Правильные многоугольники – это многоугольники, у которых все стороны и все углы равны, правильные многогранники – это многогранники, ограниченные правильными и одинаковыми многоугольниками.

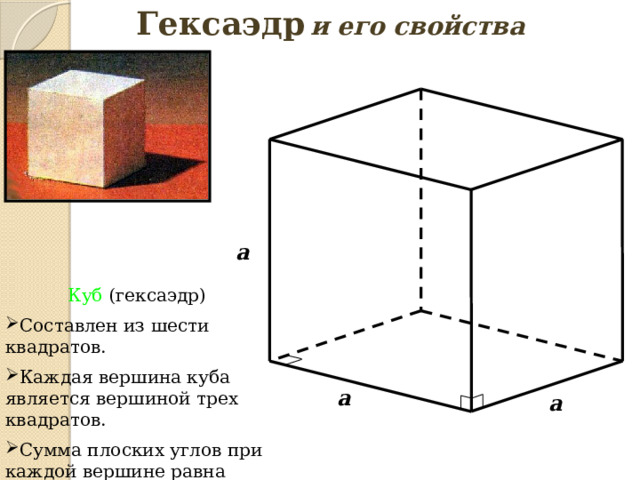
Гексаэдр и его свойства

a

Куб (гексаэдр)

• Составлен из шести квадратов.
• Каждая вершина куба является вершиной трех квадратов.
• Сумма плоских углов при каждой вершине равна 270°.

a

a

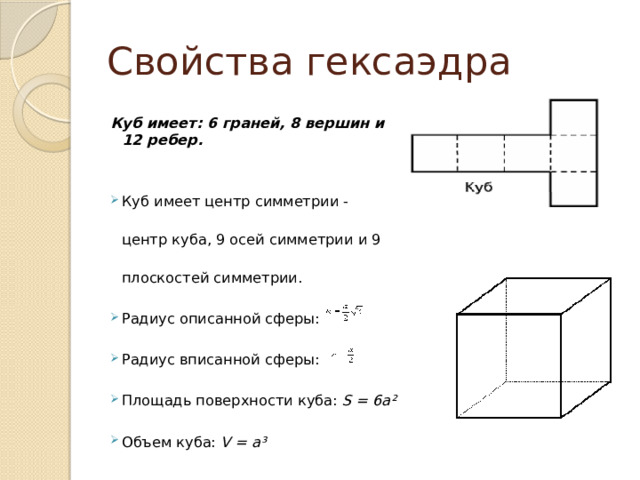
Свойства гексаэдра

Куб имеет: 6 граней, 8 вершин и 12 ребер.

• Куб имеет центр симметрии - центр куба, 9 осей симметрии и 9 плоскостей симметрии.
• Радиус описанной сферы:
• Радиус вписанной сферы:
• Площадь поверхности куба: S = 6a²
• Объем куба: V = a³

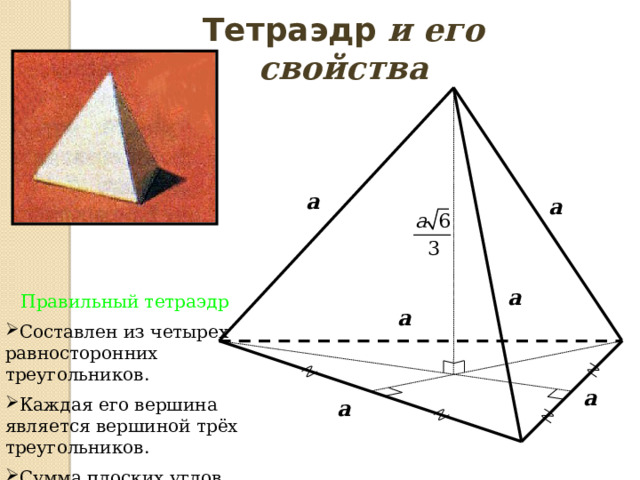
Тетраэдр и его свойства

a

a

a

Правильный тетраэдр

• Составлен из четырех равносторонних треугольников.
• Каждая его вершина является вершиной трёх треугольников.
• Сумма плоских углов при каждой вершине равна 180°.

a

a

a

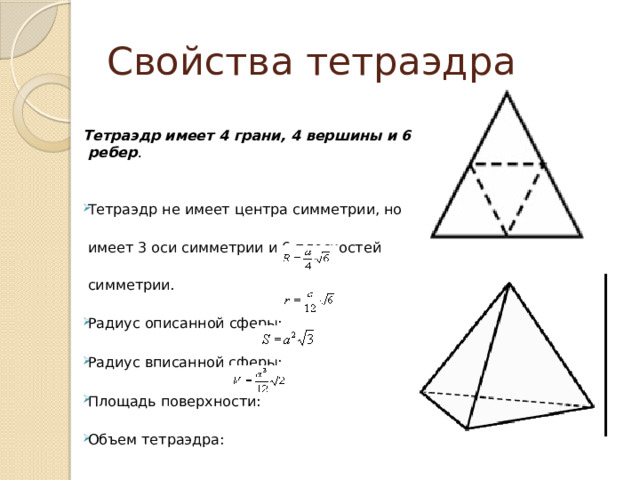
Свойства тетраэдра

Тетраэдр имеет 4 грани, 4 вершины и 6 ребер .

• Тетраэдр не имеет центра симметрии, но имеет 3 оси симметрии и 6 плоскостей симметрии.
• Радиус описанной сферы:
• Радиус вписанной сферы:
• Площадь поверхности:
• Объем тетраэдра:

Октаэдр и его свойства

a

a

a

a

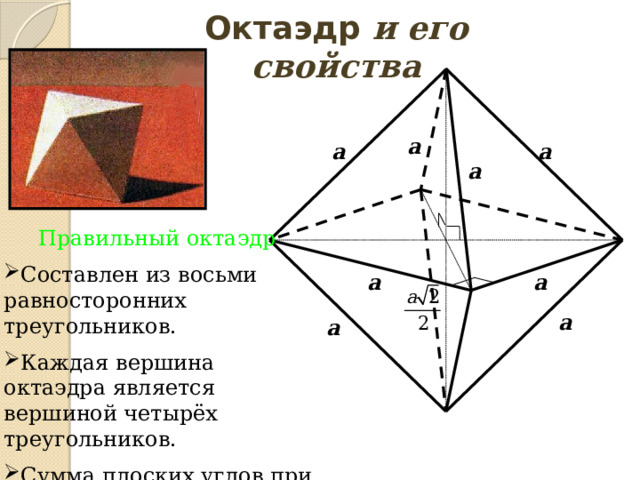
Правильный октаэдр

• Составлен из восьми равносторонних треугольников.
• Каждая вершина октаэдра является вершиной четырёх треугольников.
• Сумма плоских углов при каждой вершине 240°

a

a

a

a

Свойства октаэдра

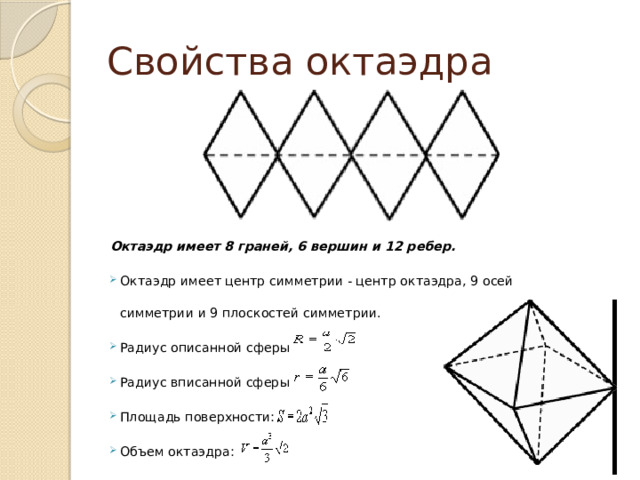
Октаэдр имеет 8 граней, 6 вершин и 12 ребер.

• Октаэдр имеет центр симметрии - центр октаэдра, 9 осей симметрии и 9 плоскостей симметрии.
• Радиус описанной сферы:
• Радиус вписанной сферы:
• Площадь поверхности:
• Объем октаэдра:

Икосаэдр и его свойства р

a

a

a

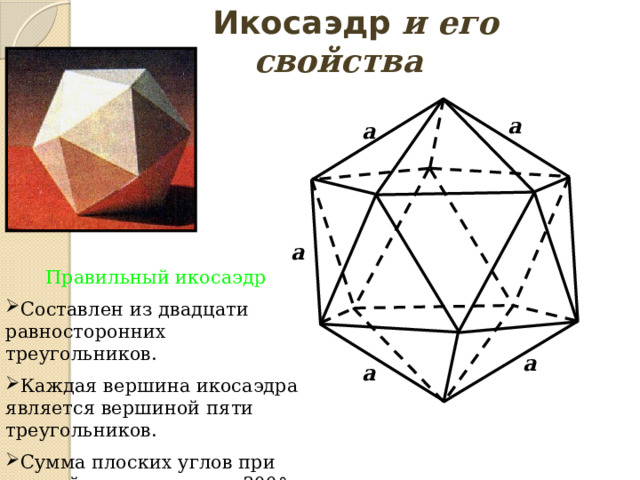
Правильный икосаэдр

• Составлен из двадцати равносторонних треугольников.
• Каждая вершина икосаэдра является вершиной пяти треугольников.
• Сумма плоских углов при каждой вершине равна 300°

a

a

Свойства икосаэдра

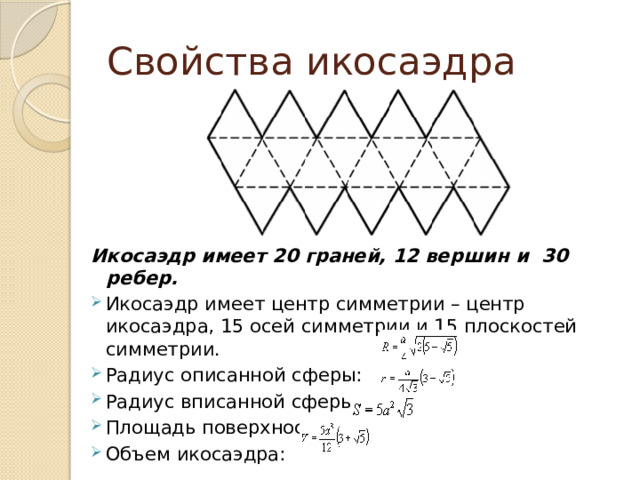
Икосаэдр имеет 20 граней, 12 вершин и 30 ребер.

• Икосаэдр имеет центр симметрии – центр икосаэдра, 15 осей симметрии и 15 плоскостей симметрии.
• Радиус описанной сферы:
• Радиус вписанной сферы:
• Площадь поверхности:
• Объем икосаэдра:

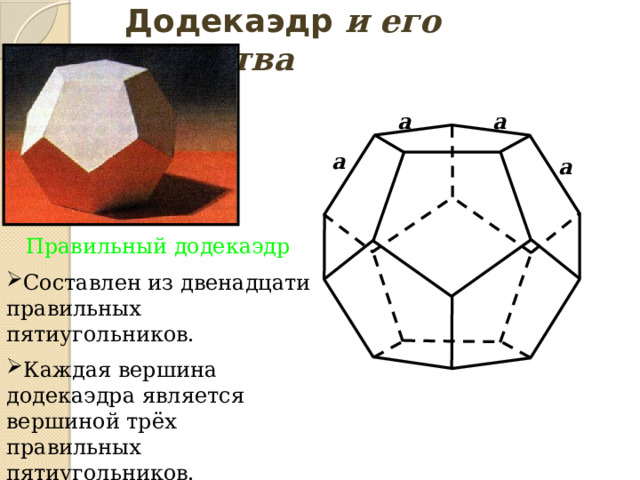
Додекаэдр и его свойства

a

a

a

a

Правильный додекаэдр

• Составлен из двенадцати правильных пятиугольников.
• Каждая вершина додекаэдра является вершиной трёх правильных пятиугольников.
• Сумма плоских углов при каждой вершине равна 324°.

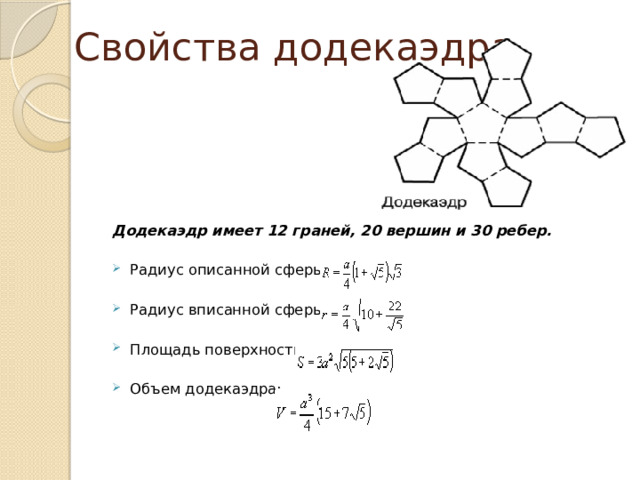
Свойства додекаэдра

Додекаэдр имеет 12 граней, 20 вершин и 30 ребер.

• Радиус описанной сферы:
• Радиус вписанной сферы:
• Площадь поверхности:
• Объем додекаэдра:

№

Название многогранника

1

2

Число вершин В

Гексаэдр

Число ребер Р

8

3

Тетраэдр

4

4

Октаэдр

12

Число граней Г

Икосаэдр

6

6

5

6

В – Р + Г

12

4

Додекаэдр

12

2

30

8

20

2

20

30

2

12

2

2

В последнем столбце получилось одинаковое число « 2» .

Это число называется Эйлеровой характеристикой в честь Леонардо Эйлера .

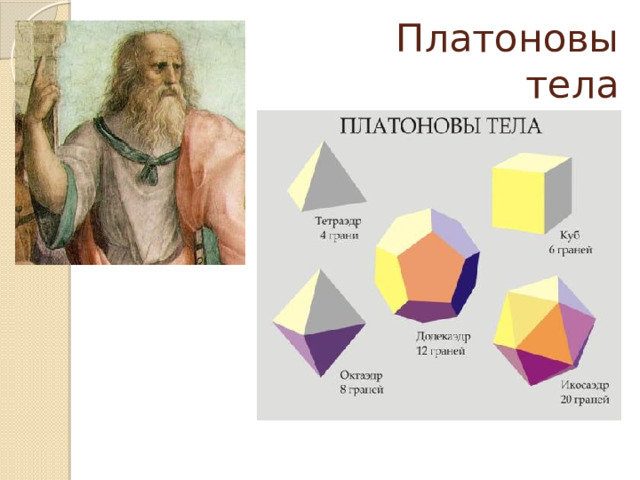
Платоновы тела

«Правильные многогранники в философской картине мира Платона».

Правильные многогранники иногда называют Платоновыми телами, поскольку они занимают видное место в философской картине мира, разработанной великим мыслителем Древней Греции Платоном (ок. 428 – ок. 348 до н.э.).

Платон считал, что мир строится из четырёх «стихий» - огня, земли, воздуха и воды, а атомы этих «стихий» имеют форму четырёх правильных многогранников. Тетраэдр олицетворял огонь, поскольку его вершина устремлена вверх, как у разгоревшегося пламени; икосаэдр – как самый обтекаемый – воду; куб – самая устойчивая из фигур – землю, а октаэдр – воздух.

В наше время эту систему можно сравнить с четырьмя состояниями вещества - твёрдым, жидким, газообразным и пламенным. Пятый многогранник – додекаэдр символизировал весь мир и почитался главнейшим.

Это была одна из первых попыток ввести в науку идею систематизации.

Преподаватель: А теперь от Древней Греции перейдём к Европе XVI – XVII вв., когда жил и творил замечательный немецкий астроном, математик Иоганн Кеплер (1571 – 1630).

Икосаэдро-додекаэдровая структура Земли

Архимедовы тела

Домашнее задание.

Подготовить дополнительные сведения.

Кроме пяти правильных многогранников существуют полуправильные многогранники, тела Архимеда.

Архимедовы тела обладают свойством: любые две вершины можно совместить так, что все грани многогранника попарно совпадут друг с другом………

………………………………………………………………………………………………………………………………………

Правильные многогранники и природа

Искусство и правильные многогранники

Леонардо да Винчи

Сальвадор Дали

Спасибо за урок!!!