
Рациональные уравнения как математические модели реальных ситуаций (8 класс)
Текстовые задачи
(ЕГЭ 11 класс, ОГЭ 9 класс)
Учитель математики И.А.Калистратова
Школа №91
Нижний Новгород

- Задача №1 (№882) (геометрического содержания)
- Задача №1.1 (супертренинг ГИА 9 класс)
- Задача №1.2 (супертренинг ГИА 9 класс)
- Задача №1.3 (супертренинг ГИА 9 класс)
- Задача №2 (тестирование 8 класс) (на работу)
- Задача №2.1 (из демоверсии ЕГЭ 11 класс)
- Задача №3 (№888) (на движение)
- Задача№3 .1 (тестирование 8 класс)
- Задача№3 .2 (тестирование 8 класс)
- Задача №3.3 (готовимся к ЕГЭ)
- Задача №4 (№884) (числа)
- Задача №4.1 (тестирование 8 класс)
- Задача №4. 2 (тестирование 8 класс)
- Задача №4. 3 (готовимся к ЕГЭ)
- Задача №5 (№935) (на концентрацию, на смеси и сплавы)
- Задача №5.1(готовимся к ЕГЭ)
- Текстовые задачи www.fipi.ru
- Текстовые задачи из открытого сегмента, ФИПИ

Задача №1 (№882)
Периметр прямоугольника равен 28 см, а сумма площадей квадратов, построенных на двух смежных сторонах прямоугольника, равна 116 см 2 . Найдите стороны прямоугольника.

I этап. Составление математической модели
P = 2(a + b)
S 1 = a 2 , S 2 = b 2
S 1 + S 2 = 116 см 2
Составим
систему
уравнений
a 2 + b 2 = 116,
2 (a + b) = 28.
? a
b
? b
P= 28см
S 1
S 2
a
 0 , 2д.к. b 1 = 10, b 2 = 4 III этап. Ответ на вопрос задачи Значит, a 1 = 14 – 10 =4(см), a 2 = 14 – 4 =10(см). Ответ: 10см и 4см. В меню " width="640"
0 , 2д.к. b 1 = 10, b 2 = 4 III этап. Ответ на вопрос задачи Значит, a 1 = 14 – 10 =4(см), a 2 = 14 – 4 =10(см). Ответ: 10см и 4см. В меню " width="640"
II этап. Работа с математической моделью
a 2 + b 2 = 116,
a + b = 14,
a = 14 – b ,
(14 – b ) 2 + b 2 = 116,
96 – 28 b + b 2 + b 2 = 116
2 b 2 - 28 b + 80 = 0
b 2 - 14 b + 40 = 0
Д = 9 0 , 2д.к. b 1 = 10, b 2 = 4
III этап. Ответ на вопрос задачи
Значит, a 1 = 14 – 10 =4(см),
a 2 = 14 – 4 =10(см).
Ответ: 10см и 4см.
В меню

Задача №1.1 (супертренинг ГИА 9 класс)
Периметр прямоугольника равен 30 см. Длины смежных сторон относятся как 2 : 1. Найдите длины сторон этого прямоугольника.
Пусть a и b – стороны прямоугольника, причём
a – большая сторона. Какая система уравнений
не соответствует условию задачи?
3)
1)
2)
4)
В меню

ВЕРНО!
В меню

НЕВЕРНО!

Задача №1.2 (супертренинг ГИА 9 класс)
Периметр прямоугольника равен 10 см. Длины смежных сторон относятся как 4 : 1. Найдите длины сторон этого прямоугольника.
Пусть a и b – стороны прямоугольника, причём
a – большая сторона. Какая система уравнений не соответствует условию задачи?
3)
1)
4)
2)
В меню

НЕВЕРНО!

Задача №1.3 (супертренинг ГИА 9 класс)
Периметр прямоугольника равен 20 см. Длины смежных сторон относятся как 3 : 2. Найдите длины сторон этого прямоугольника.
Пусть a и b – стороны прямоугольника, причём
a – большая сторона. Какая система уравнений не соответствует условию задачи?
1)
3)
2)
4)
В меню

НЕВЕРНО!

Задача №2 (тестирование 8 класс)
Два секретаря подготовили пакет документов за 12 часов. Сколько времени потребовалось бы первому из них на подготовку этого пакета, если он может выполнить всю работу на 10 часов быстрее второго?
В меню
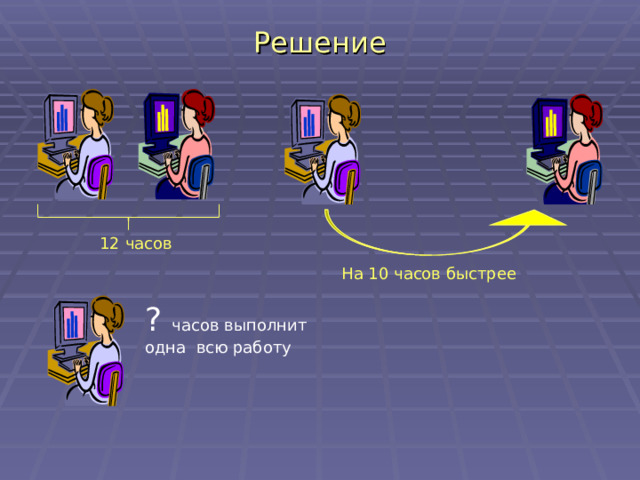
Решение
12 часов
На 10 часов быстрее
? часов выполнит одна всю работу
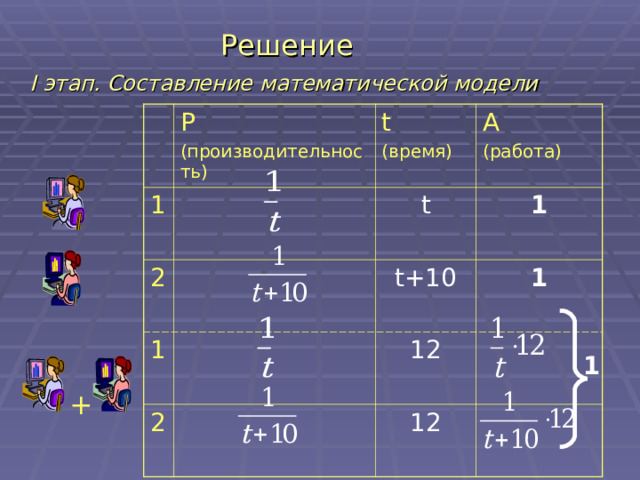
Решение
I этап. Составление математической модели
P
(производительность)
1
t
(время)
2
1
A
( работа)
t
1
2
t+10
1
12
12
1
+

II этап. Работа с математической моделью
III этап. Ответ на вопрос задачи
- 6 0 ( не удовлетворяет условию задачи)
Ответ: 20.
В меню

Задача №2.1 (из демоверсии ЕГЭ 11 класс, 2009г.)
Двое рабочих, работая вместе, могут выполнить работу за 12 дней. За сколько дней, работая отдельно, выполнит эту работу первый рабочий, если он за два дня выполняет такую же часть работы, какую второй – за три дня?
В меню
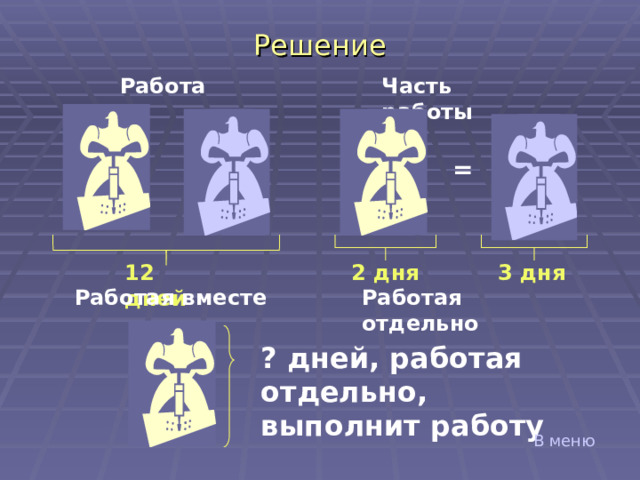
Решение
Часть работы
Работа
=
12 дней
2 дня
3 дня
Работая отдельно
Работая вместе
? дней, работая отдельно, выполнит работу
В меню

Примем объём работы за 1.
Т.к. вместе выполняют работу за 12 часов, то
x часов для выполнения
всей работы
– производительность
первого рабочего
y часов для выполнения
всей работы
– производительность
первого рабочего
∙ 3 – часть работы,
которую выполняет
второй рабочий за 3 дня
∙ 2 – часть работы,
которую выполняет
первый рабочий за 2 дня

Получаем систему уравнений
…
x = 20
y = 30
Ответ: 20.
В меню

Задача №3 (№888)
Велосипедист проехал 18 км с определённой скоростью, а оставшиеся 6 км со скоростью на 6 км / ч меньше первоначальной. Найдите скорость велосипедиста на втором участке пути, если на весь путь он затратил 1,5 ч.
В меню
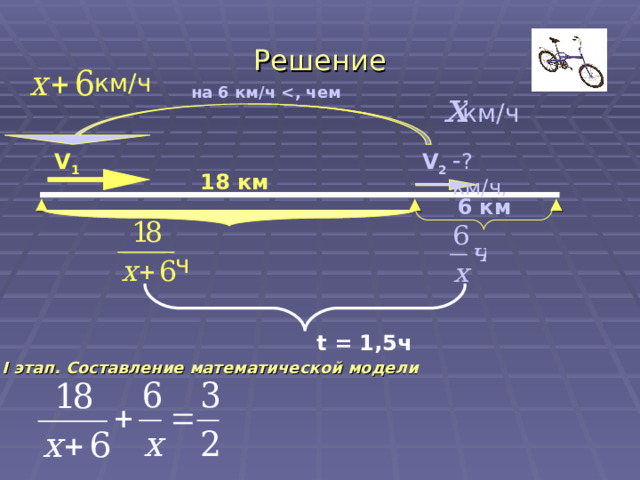
Решение
км / ч
на 6 км / ч , чем
км / ч
- ? км / ч ,
V 2
V 1
18 км
6 км
▲
▲
▲
ч
t = 1,5 ч
I этап. Составление математической модели

II этап. Работа с математической моделью
III этап. Ответ на вопрос задачи
- 2 – не удовлетворяет условию задачи
В меню
Ответ: 12 км / ч .

Задача№3 .1 (тестирование 8 класс)
Составьте уравнение для решения задачи, приняв за x скорость велосипедиста.
Из посёлка в город выехал велосипедист. Через 2 часа вслед за ним из посёлка выехал мотоциклист, скорость которого на 15 км / ч больше скорости велосипедиста. В город они прибыли одновременно. Найдите скорость велосипедиста, если расстояние от посёлка до города 60 км.
3)
1)
2)
4)
В меню

НЕВЕРНО!

Задача№3 .2 (тестирование 8 класс)
Составьте уравнение для решения задачи, приняв за x скорость автобуса.
Из посёлка в город выехал автобус. Через 1 час навстречу ему из города в посёлок выехал легковой автомобиль, скорость которого на 20 км / ч больше скорости автобуса. Они встретились на середине дороги, соединяющей посёлок и город. Найдите скорость легкового автомобиля, если расстояние от посёлка до города 480 км.
3)
1)
2)
4)
В меню

НЕВЕРНО!

Задача №3.3 (готовимся к ЕГЭ)
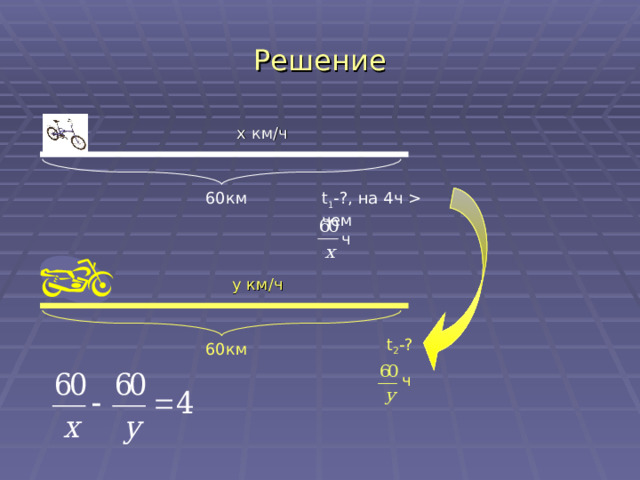
На 60 км пути велосипедист тратит на 4 ч больше времени, чем мотоциклист. Если же он увеличит скорость на 3 км / ч, то на тот же путь потратит в 4 раза больше времени, чем мотоциклист. Найдите скорость велосипедиста.
В меню
 чем 60км ч y км / ч t 2 - ? 60км ч " width="640"
чем 60км ч y км / ч t 2 - ? 60км ч " width="640"
Решение
x км / ч
t 1 - ?, на 4ч чем
60км
ч
y км / ч
t 2 - ?
60км
ч
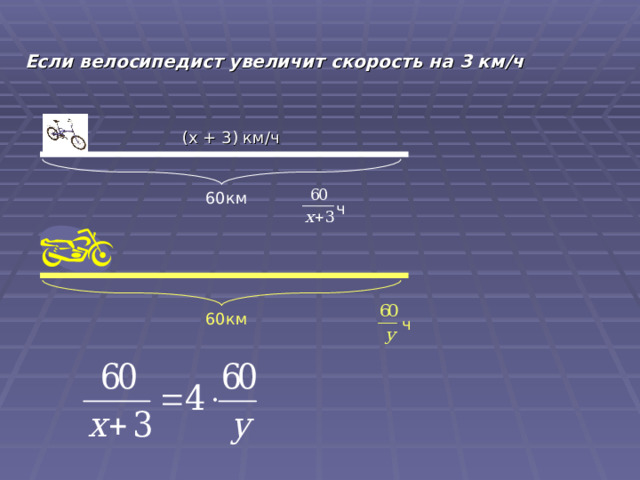
Если велосипедист увеличит скорость на 3 км / ч
( x + 3 ) км / ч
60км
ч
60км
ч

Рассмотрим систему уравнений:
Решаем второе уравнение:
15 x = 60( x+3 ) - 4 x ( x+3 );
x ( x+3 ) ≠ 0

4 x 2 – 33 x – 180 = 0;
x 1 = 12;
x 2 = - – не удовлетворяет условию задачи.
Ответ: 12.
В меню

Задача №4 (№884)
Сумма квадратов двух последовательных натуральных чисел больше их произведения на 307. Найдите эти числа.
I этап. Составление математической модели
n 2 + (n + 1) 2 – сумма квадратов чисел,
n(n + 1) - произведение чисел
n
n + 1
В меню

По условию задачи составим модель
n 2 + (n + 1) 2 - n(n + 1) = 307
II этап. Работа с математической моделью
…
n 2 + n – 306 = 0
n 1 = 34, n 2 = -36
III этап. Ответ на вопрос задачи
n 1 = 34, n 2 = -36 ( не удовлетворяет условию задачи)
n + 1 = 34 + 1 = 35
Ответ: 34, 35.
В меню

Задача №4.1 (тестирование 8 класс)
Составьте уравнение к задаче, приняв за x меньшее из чисел.
Одно из чисел на 17 больше другого, а их произведение равно 468. Найдите эти числа.
- x ( x +17) = 468
- 2 x – 17 = 468
- x ( x -17) = 468
- 2 x + 17 = 468
В меню

НЕВЕРНО!

Задача №4. 2 (тестирование 8 класс)
Составьте уравнение к задаче, приняв за x меньшее из чисел.
Одно из чисел на 11 меньше другого, а их произведение равно 534. Найдите эти числа.
- 2 x +11 = 534
- 2 x – 11 = 534
- x ( x -11) = 534
- x ( x + 1 1) = 534
В меню

НЕВЕРНО!
 y то x - 4 = y В меню " width="640"
y то x - 4 = y В меню " width="640"
Задача №4. 3 (готовимся к ЕГЭ)
Найдите двузначное число, если количество единиц в нём на 4 больше количества десятков, а произведение искомого числа на сумму его цифр равно 90.
Решение:
x – количество
единиц в записи
данного числа,
y – количество десятков.
10 y + x x на 4 y
то x - 4 = y
В меню

Решение
10 y + x - искомое число
Согласно второму условию,
(10 y + x ) ∙ ( x + y ) = 90
Решим систему уравнений:
x - 4 = y ,
(10 y + x ) ∙ ( x + y ) = 90

Очевидно решение системы способом подстановки .
y = x – 4,
(10(x-4) + x)(x +x – 4) = 90.
Решаем второе уравнение:
(11 x – 40)(2x – 4) = 90
( 11 x – 40)(x – 2) = 45;
11x 2 – 62x + 80 = 45;
11x 2 – 62x +35 = 0.
Корни: x 1 = 5; x 2 = (не удовлетворяет условию задачи).
В искомом числе 5 единиц, , десятков: 5 – 4 = 1.
Получим число: 10 ∙ 1 + 5 = 15.
Ответ:15.
В меню

Задача №5 (№935)
Сплав меди и цинка, содержащий 5 кг цинка, сплавили с 15 кг цинка, после чего содержание цинка в сплаве повысилось на 30%. Какова первоначальная масса сплава, если известно, что в нём меди было больше, чем цинка?
В меню
 ( x + 5 + 15) кг на 30% повысилось содержание " width="640"
( x + 5 + 15) кг на 30% повысилось содержание " width="640"
Медь
Цинк
5кг
Цинк
Медь
Масса сплава ?
( x + 5) кг
Цинк 15кг
x кг
( x + 5 + 15) кг
на 30% повысилось содержание

Решение
I этап
Пусть в сплаве x кг меди, тогда ( x + 5) кг – масса первоначального сплава,
( x + 5 + 15) кг – масса полученного сплава.
- процентное содержание цинка
в первоначальном сплаве,
- процентное содержание цинка
в полученном сплаве. Составим математическую модель задачи – уравнение
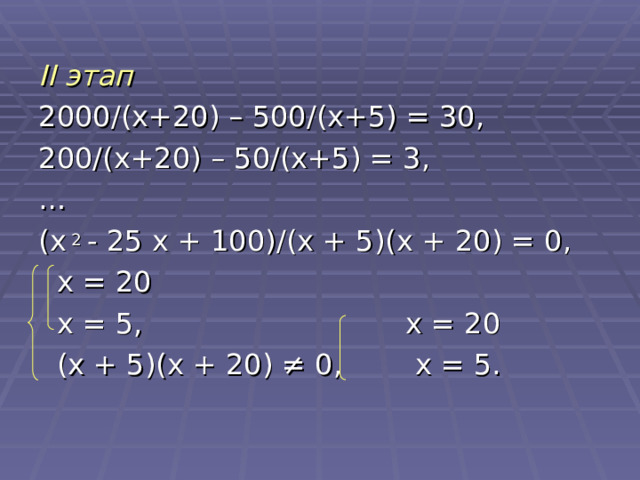
II этап
2000 /(x+20) – 500/ ( x +5) = 30,
200 / ( x +20) – 50 / ( x +5) = 3,
…
( x 2 - 25 x + 100) / ( x + 5)( x + 20) = 0,
x = 20
x = 5, x = 20
( x + 5)( x + 20) ≠ 0, x = 5.

III этап
Т.к. первоначально было 5 кг цинка, а меди больше, чем цинка, то выбираем x = 20. Значит, масса сплава
5 + 20 = 25 (кг).
Ответ:25 кг.
В меню

Задача №5.1(готовимся к ЕГЭ)
Если слить 8 кг и 2 кг растворов серной кислоты разной концентрации, то получится 12%-ный раствор кислоты. При смешивании двух одинаковых масс тех же растворов получим 15%-ный раствор. Определите первоначальную концентрацию каждого раствора.
В меню

Анализ
Концентрация раствора – это процентное выражение отношения массы растворённого вещества к общей массе раствора.
При решении задач такого типа следует иметь ввиду , что во время смешивания сохраняются все массы, изменяется только их отношение.
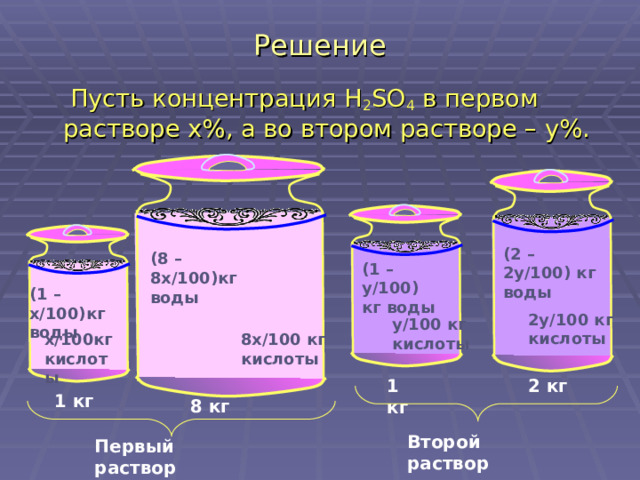
Решение
Пусть концентрация H 2 SO 4 в первом растворе x% , а во втором растворе – y%.
(2 – 2 y/100) кг воды
(8 – 8 x/100) кг воды
(1 – y/100) кг воды
(1 – x/100 )кг воды
2 y/100 кг кислоты
y/100 кг кислоты
x/100 кг кислоты
8 x/100 кг кислоты
1 кг
2 кг
1 кг
8 кг
Второй раствор
Первый раствор

После смешивания получим раствор общей массой 10 кг
По условию получаем
раствор 12%-ной
концентрации, ,в 10кг
р-ра будет 10 ∙ 12 /100 кг
кислоты. Получаем:
Преобразуем:
4 x + y=60
кг
кислоты
10 кг

Рассмотрим вторую ситуацию
Т.к. смесь получиться
15%-ной концентрации,
то в (1 + 1) кг смеси
должно содержаться
Ответ: 10 и 20.
кг
кислоты
кг
кислоты
кг кислоты
1 кг
1 кг
Получаем:
После преобразований: x + y = 30
Решим систему уравнений:
В меню
Текстовые задачи из открытого сегмента 2009г., ФИПИ
1 2 3 4 5
Два оператора, работая вместе, могут набрать 40 страниц текста за 1ч. Работая отдельно, первый оператор на набор 90 страниц этого текста тратит на 5 ч больше, чем второй оператор на набор 25 страниц. За сколько часов второй оператор сможет набрать 275 страниц этого текста?
Ответ: 11.
В меню

Текстовые задачи из открытого сегмента 2009г., ФИПИ
1 2 3 4 5
Пешеход рассчитывает попасть на станцию, расположенную в 20 км, к приходу поезда. Через 2,5 ч после отправления он сделал остановку на 15 мин, а затем увеличил первоначальную скорость на 1 км/ч и пришел на станцию к приходу поезда. С какой скоростью шел пешеход после остановки?
Ответ:6.
В меню

Текстовые задачи из открытого сегмента 2009г., ФИПИ
1 2 3 4 5
Набор химических реактивов состоит из трех веществ. Массы первого, второго и третьего веществ в этом наборе относятся как 5:8:12 . Массу первого вещества увеличили на 8%, а второго – на 4%. На сколько процентов надо уменьшить массу третьего вещества, чтобы масса всего набора не изменилась?
Ответ: 6.
В меню

Текстовые задачи из открытого сегмента 2009г., ФИПИ
1 2 3 4 5
Катер прошел 5 км против течения реки, а затем 21 км по течению, затратив на весь путь 1 ч. Найдите собственную скорость катера, если скорость течения реки 4 км/ч.
Ответ: 0,7
В меню

Текстовые задачи из открытого сегмента 2009г., ФИПИ
1 2 3 4 5
Две машинистки, работая вместе, могут напечатать 22 страницы текста за 1 ч. Чтобы напечатать 120 страниц текста, первая машинистка потратит на 2 ч больше, чем вторая. За сколько часов первая машинистка сможет напечатать 300 страниц?
Ответ: 2.
В меню


 Получите свидетельство
Получите свидетельство Вход
Вход












 Рациональные уравнения как математические модели реальных ситуаций (1.7 MB)
Рациональные уравнения как математические модели реальных ситуаций (1.7 MB)
 0
0 360
360 9
9 Нравится
0
Нравится
0


