Получите свидетельство
Вход
6.04.2020
Классная работа
«Расстояние от
точки до прямой.
Расстояние от
точки до прямой»
Устная работа
- Какой угол называется внешним углом треугольника?
- Соотношение между углами и сторонами в треугольнике?
- Как звучит неравенство треугольника?
- Как называются стороны в прямоугольном треугольнике?
- Какая сторона является наибольшей в прямоугольном треугольнике? Почему?
- Свойства в прямоугольном треугольнике (3), проговорить вслух (из п.34, кто забыл)
- Признаки равенства прямоугольных треугольников (4) (из п.35)
Устная работа
- Какие прямые называются перпендикулярными?
- Что называют перпендикуляром, проведенным из данной точки к данной прямой?
( это отрезок, лежащий на прямой, перпендикулярной данной, которая проходит через данную точку)
- Сколько перпендикуляров можно провести из точки к данной прямой?
перпендикуляр
наклонная
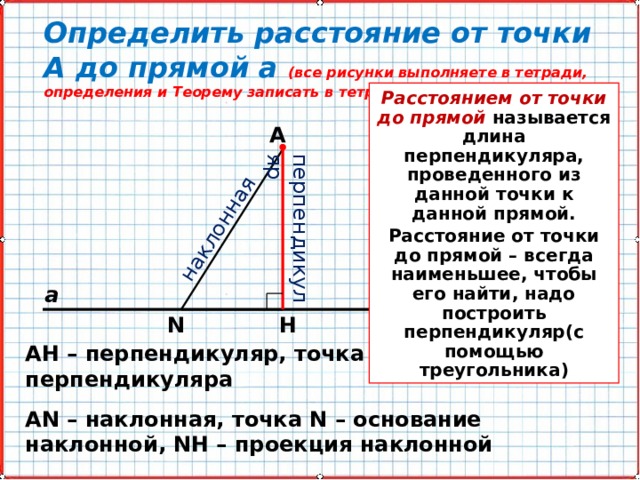
Определить расстояние от точки А до прямой а (все рисунки выполняете в тетради, определения и Теорему записать в тетрадь)
Расстоянием от точки до прямой называется длина перпендикуляра, проведенного из данной точки к данной прямой.
Расстояние от точки до прямой – всегда наименьшее, чтобы его найти, надо построить перпендикуляр(с помощью треугольника)
А
a
N
H
АН – перпендикуляр, точка Н – основание перпендикуляра
АN – наклонная, точка N – основание наклонной, NH – проекция наклонной
перпендикуляр
наклонная
А
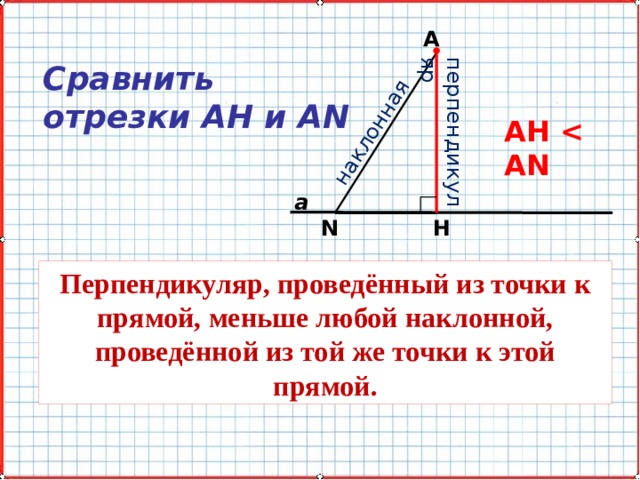
Сравнить отрезки АH и АN
АH
a
H
N
Перпендикуляр, проведённый из точки к прямой, меньше любой наклонной, проведённой из той же точки к этой прямой.
Выписать в тетрадь
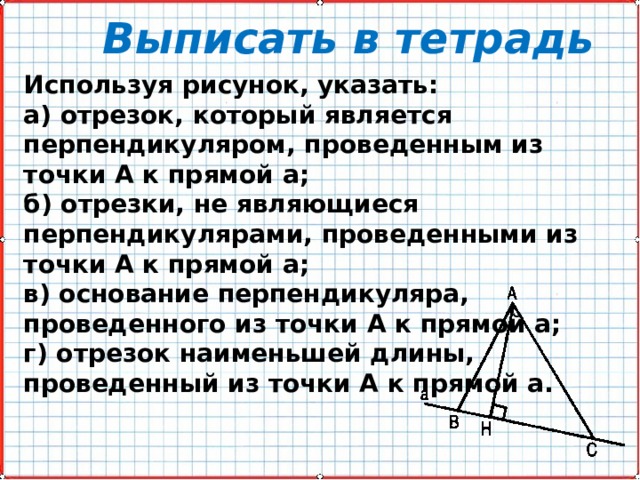
Используя рисунок, указать:
а) отрезок, который является перпендикуляром, проведенным из точки А к прямой а;
б) отрезки, не являющиеся перпендикулярами, проведенными из точки А к прямой а;
в) основание перпендикуляра, проведенного из точки А к прямой а;
г) отрезок наименьшей длины,
проведенный из точки А к прямой а.
Теорема:
Все точки каждой из двух параллельных прямых равноудалены от другой прямой.
~
Если a || b, AB b, MN b, то AB = MN.
Доказательство:
M
A
a
Доп. построение: АN
Если MN b , то MN a.
Δ ABN = Δ NMA (по гипотенузе и острому углу)
b
N
B
Следовательно, AB = MN .
Теорема доказана.
7
Следствия из теоремы: (записать в тетрадь)
- Все точки плоскости, расположенные по одну сторону от данной прямой и равноудаленные от нее, лежат на прямой, параллельной данной (утверждение, обратное теореме).
- Множество всех точек плоскости, находящихся на данном расстоянии от данной прямой и лежащих по одну сторону от нее, есть прямая, параллельная данной.
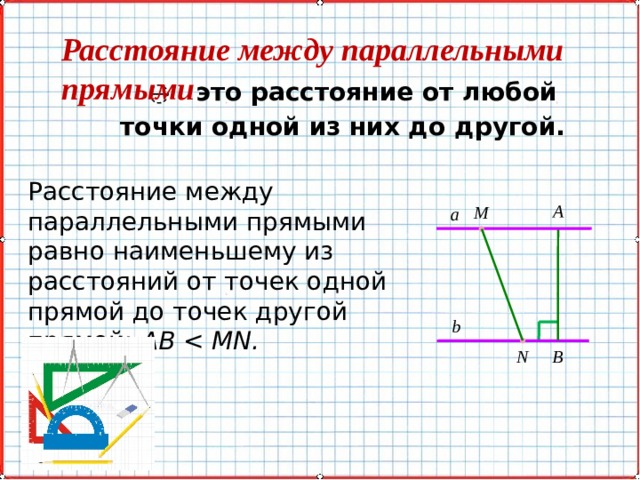
Расстояние между параллельными прямыми
̶ это расстояние от любой
точки одной из них до другой.
Расстояние между параллельными прямыми равно наименьшему из расстояний от точек одной прямой до точек другой прямой: AB MN.
A
M
a
b
B
N
9
Решение задач
1. В треугольнике АВС АВ = ВС = 20 см, АВС = 120°. Найти расстояние от вершины В до прямой АС.( букву на стороне AC поставьте сами, воспользуйтесь одним из свойств прямоуг.
треугольников)
2) ВD – биссектриса прямоугольного треугольника АВС с
прямым углом С. Доказать, что точка D равноудалена от
прямых ВС и АВ.( проведите перпендикуляр на чертеже из D к AB, равенство сторон взять из равенства прямоугольных треугольников)
3) На рисунке СF – биссектриса
∆ СDЕ, DH – высота, С = 60°,
СО = 12 см. Найти расстояние
от точки О до прямых СЕ и СD.
( указание: построить перпендикуляр к СD,
доказать рав-во прямоугольных треугольников
(это всегда по двум элементам),
воспользоваться одним из свойств прямоуг.
треугольников).
Домашнее задание
для всех
- Изучить материал на стр. 82 – 84(параграф 4,п.37, выучить правила, теорему с доказательством
- Решить № 271, 272, 274
(используйте признаки равенства прямоугольных треугольников)
Расстояние от точки до прямой. Расстояние между параллельными прямыми (1.01 MB)
0
408
32
Нравится
0
