Расчет вероятности по формуле Бернулли

Корнюшина Татьяна Анатольевна
учитель математики, МБОУ «Гимназия №4», г. Брянск

Цель:

-формирование вероятностно-статистическое мышление учащихся;

-мотивация учащихся к изучению тем теории вероятностей;

-ознакомление с применением формулы Бернулли при решении задач.

Задачи:

-закрепить знания и умения решать комбинаторные задачи;

- формировать навыки применения схемы Бернулли при решении задач,

-формировать навыки решения задач по формуле Бернулли,

-развивать основные мыслительные операции учащихся: умение сравнивать, анализировать.

Тип урока: изучение нового материала.

Формы работы: фронтальная, индивидуальная, групповая.

Оборудование: компьютер, презентация.

Ход урока:

Актуализация знаний.

Вспомним основные понятия и формулы комбинаторики.

1. Что называется факториалом числа n?

Это произведение первых натуральных n чисел от 1 до n.

2.Сколькими способами можно расставить 4 различные книги на полке?

3! = 3·2·1

Это число перестановок из 3 элементов.

3. Сколькими способами можно распределить I, II, III места между 7 участниками соревнования?

7·6·5=210

Это число размещений из 7 элементов по 3.

4. Сколькими способами можно составить график дежурства 3 учащихся из 5?

Презентация (слайд 1)

5. Сформулируйте классическое определение вероятности.

Презентация (слайд 2)

Презентация (слайд 3)

Организационный момент.

(Сообщение темы, целей и задач урока)

Презентация (слайд 4)

Изучение нового материала.

При практическом применении теории вероятностей и математической статистики часто приходится встречаться с задачами, в которых один и тот же опыт повторяется неоднократно. В результате каждого опыта может появиться или не появиться событие A, причем нас интересует не результат каждого опыта, а общее число появлений события A в серии опытов. Например, если производится серия выстрелов по одной и той же цели, то нас, как правило, интересует не результат каждого отдельного выстрела, а общее число попаданий. При этом результаты предыдущих опытов никак не сказываются на последующих.

Такая стандартная схема часто встречается и в самой теории вероятностей. Она называется схемой независимых испытаний или схемой Бернулли. Швейцарский математик XVII в. Якоб Бернулли объединил примеры и вопросы такого типа в единую вероятностную задачу-схему (работа "Искусство предположений" опубликована в 1713 году).

Историческая справка. Якоб Бернулли (27.12.1654, Базель, - 16.8.1705, там же) - профессор математики Базельского университета (1687) был выходцем из Голландии.

Вам дома надо было вычислить вероятность выпадения 6 на игральном кубике.

(Ученики называют результаты. Вывод: результаты могут зависеть и от размера кубика. от силы бросания и т.п.)

Несколько опытов называются независимыми, если вероятность исхода каждого из опытов не зависит от того, какие исходы имели другие опыты. Например, несколько последовательных бросаний монеты - это независимые опыты. Несколько последовательных выниманий карты из колоды - независимые опыты при условии, что вынутая карта каждый раз возвращается в колоду и карты перемешиваются. В противном случае - это зависимые опыты.

Презентация (слайд 5)

.

Примеры.

Монета бросается n раз.

Из колоды извлекается карта n раз, причём каждый раз карта возвращается, колода перемешивается.

Исследуется n изделий некоторого производства, наугад выбранные, на качество.

Стрелок стреляет по мишени n раз и т.д.

Задание.

№1. Объясните, почему следующие вопросы укладываются в схему Бернулли. Укажите, в чем состоит «успех» и чему равны n и k.

а) Какова вероятность трехкратного выпадения «двойки» при десяти бросаниях игрального кубика?

б) Какова вероятность того, что при ста бросаниях монеты «орел» появится 73 раза?

в) Двадцать раз подряд бросили пару игральных кубиков. Какова вероятность того, что сумма очков ни разу не была равна десяти?

г) Из колоды в 36 карт вытащили три карты, записали результат и возвратили их в колоду, затем карты перемешали. Так повторялось 4 раза. Какова вероятность того, что каждый раз среди вытащенных карт была дама пик?

Решение. Ответы учащихся с использованием слайда 5 (парная работа).

Схема Бернулли предполагает, что один и тот же эксперимент повторяется в неизменных условиях, независимо, n раз; мы наблюдаем за появлением («успеха») или непоявлением («неудача») в каждом эксперименте одного и того же события А, вероятность появления которого в каждом эксперименте постоянна и равна p. Подсчитываем, сколько раз в серии из n повторных экспериментов произойдет событие А; k – это число «успехов» в серии из n испытаний.

а) Эксперимент – бросание кубика, число повторений n = 10.

Событие А – «выпало 2 очка» (Р(А)=const); успех – появление события А (появление двойки), число успехов k=3.

б) Эксперимент – бросание монеты, число повторений n = 100, событие А – «выпал орел» (Р(А)==const), успех – появление события А (появление «орла»), число успехов k=73.

в) Эксперимент – бросание двух кубиков одновременно, число повторений n =20, событие А – «сумма выпавших очков равна 10» (Р(А)==const), успех – появление события А (сумма выпавших очков оказалась 10); число успехов k = 0.

г) Эксперимент – извлечение одновременно трех карт из колоды 36 карт, число повторений n= 4, событие А – «среди извлеченных карт есть дама пик» (Р(А)==const), успех – появление события А (появление дамы пик в наборе); число успехов k= 4.

Ответ: а) n = 10, k=3; б) n =100, k =73; в) n = 20, k = 0; г) n = 4, k = 4.

Замечание. При решении этой задачи учащимся не нужно вычислять Р(А), достаточно сказать, что событие А имеет одну и ту же вероятность при каждом повторении эксперимента.

Презентация (слайд 6)

Решение заданий

Пример 1. Монета бросается 6 раз. Какова вероятность выпадения герба 0, 1, …6 раз?

Решение. Число опытов n=6. Событие А – «успех» – выпадение герба. Тогда .

;

;

;

;

;

;

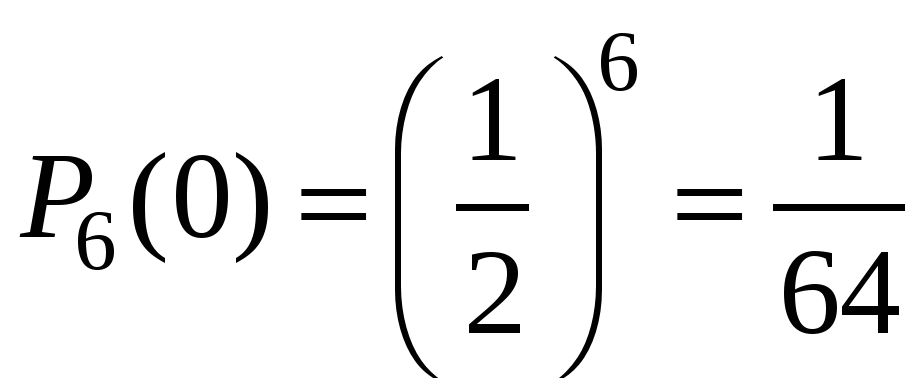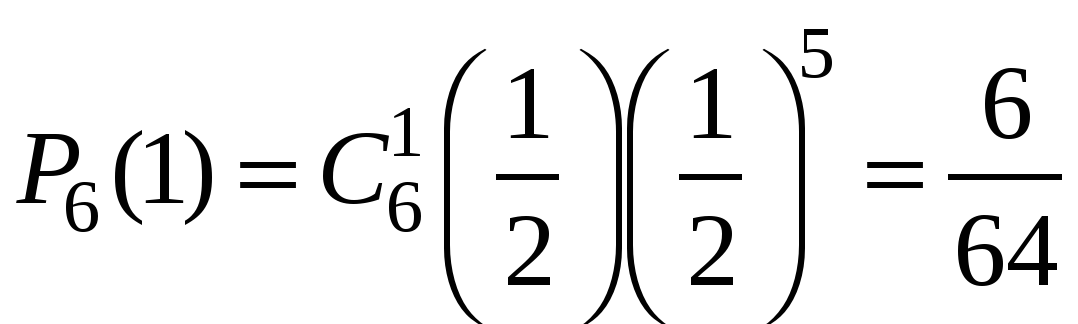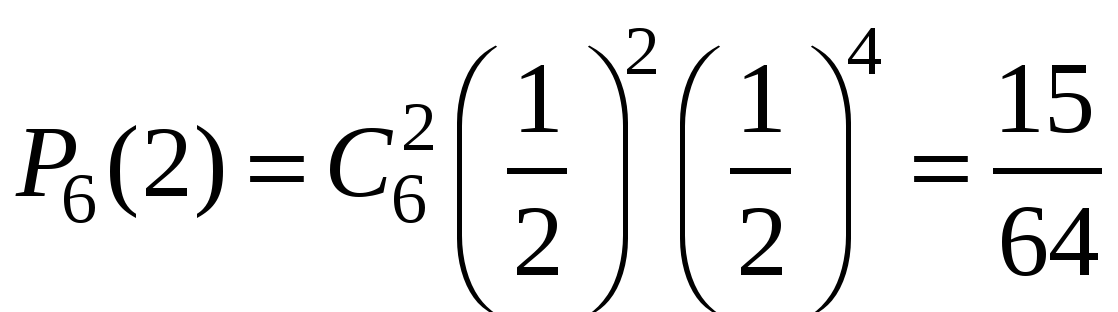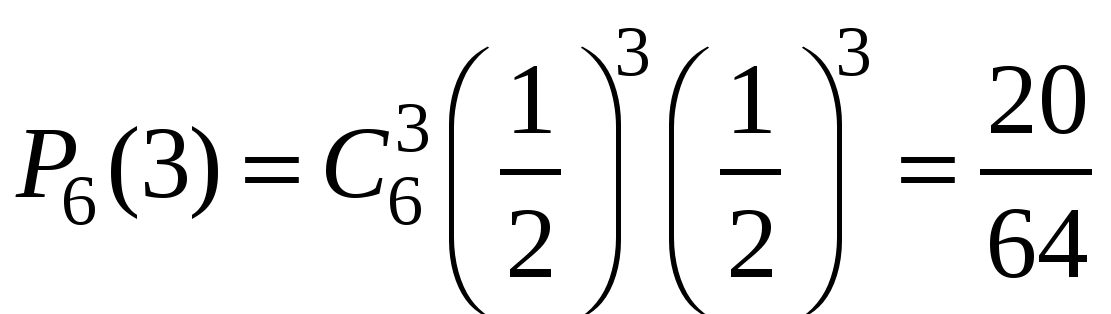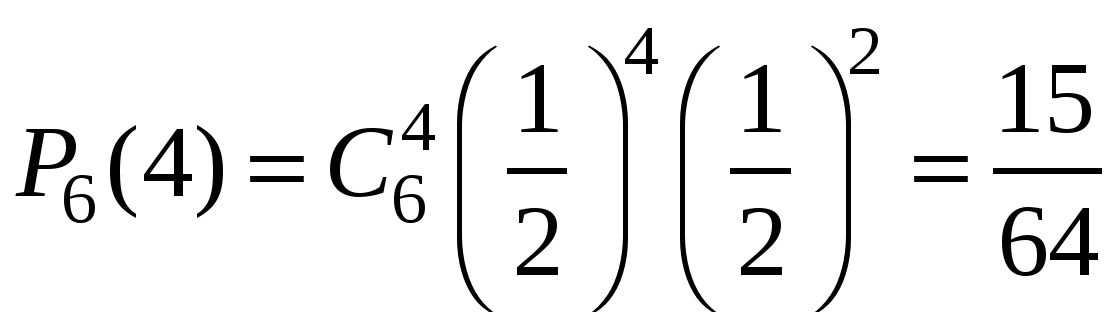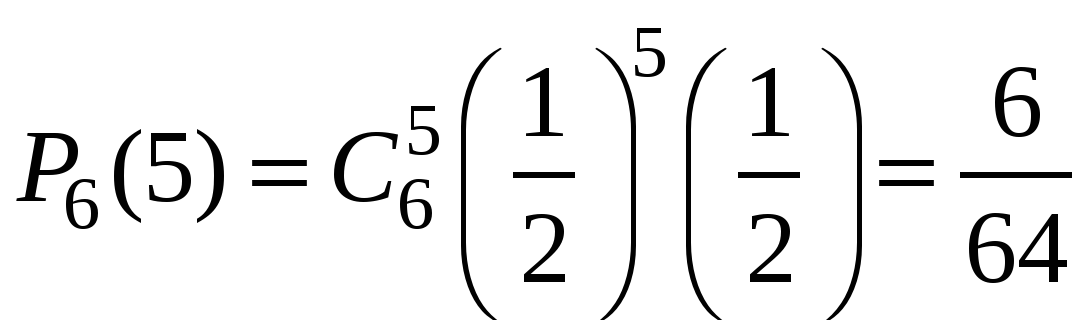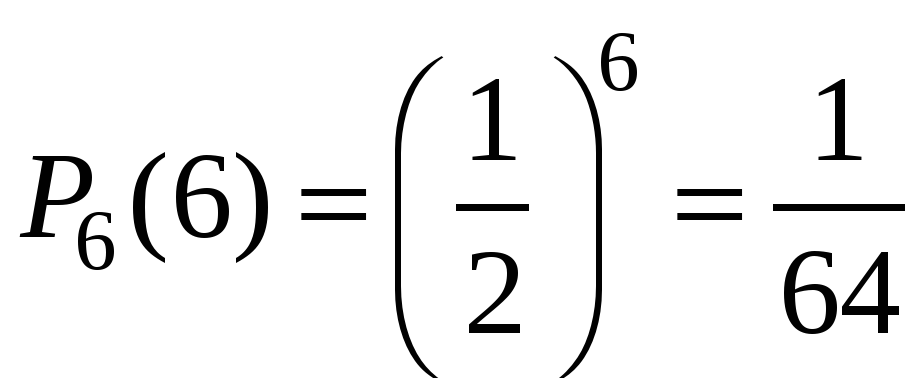
Очевидно, что наиболее вероятное число выпадений герба равно трём. Но далеко не каждый раз при шести бросаниях монеты герб выпадет ровно три раза! Вероятность говорит о том, что это будет происходить меньше, чем в трети случаях.

Пример 2. Монета бросается 10 раз. Какова вероятность двукратного появления герба?

Решение. Число опытов n=10, m= 2. Событие А – «успех» – выпадение герба. Тогда .

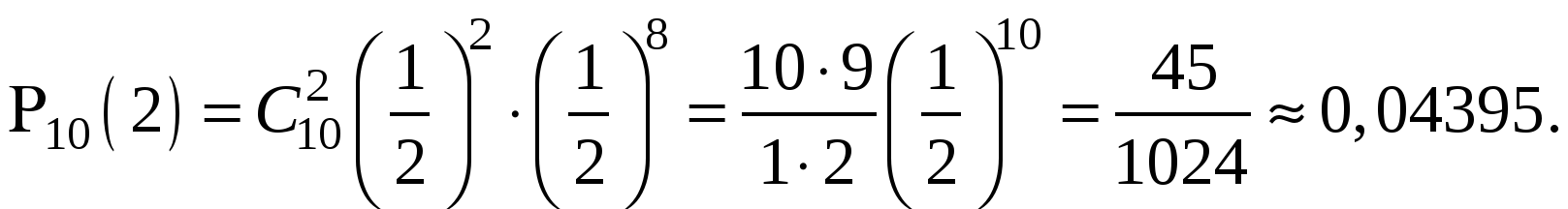
Ответ: 0,04395.

Пример 3. Вероятность того, что изделие не пройдет контроля, равна 0,125. Какова вероятность того, что среди 12 изделий не будет ни одного забракованного контролером?

Решение. Число опытов n=12, m=0. Событие А – «успех» – не будет ни одного забракованного. Тогда .

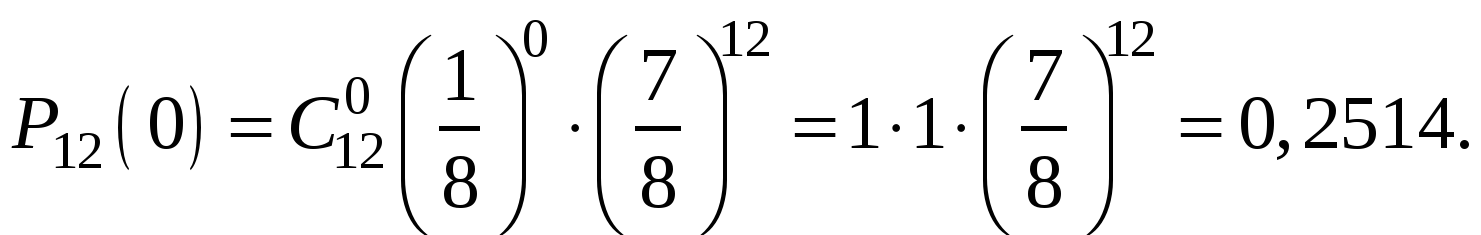
Ответ: 0,2514.

Домашнее задание

В следующих испытаниях найдите вероятности «успеха» и «неудачи».

а) Бросают пару различных монет. «Неудача» - выпадение двух «орлов».

б) Бросают игральный кубик. «Успех» - выпадение числа, кратного трем.

в) Бросают пару различных кубиков. «Неудача» - выпадение двух четных чисел.

г) Из 36 игральных карт берут 5. «Успех» - среди них нет дамы пик.

Решение.

а) Общее число исходов эксперимента n=2·2=4; вероятность «неудачи» ; вероятность «успеха» .

б) n=6; исходы, благоприятствующие «успеху» - выпадение 3 и 6 очков; ; вероятность «успеха» ; вероятность «неудачи» .

в) n=6·6=36; количество исходов, благоприятствующих «неудаче», (на каждом кубике 3 четные числа); вероятность «неудачи» ; вероятность «успеха» .

г) =376992; количество исходов, благоприятствующих «успеху», равно (выбираем карту из колоды без дамы пик);

вероятность «успеха» = = ,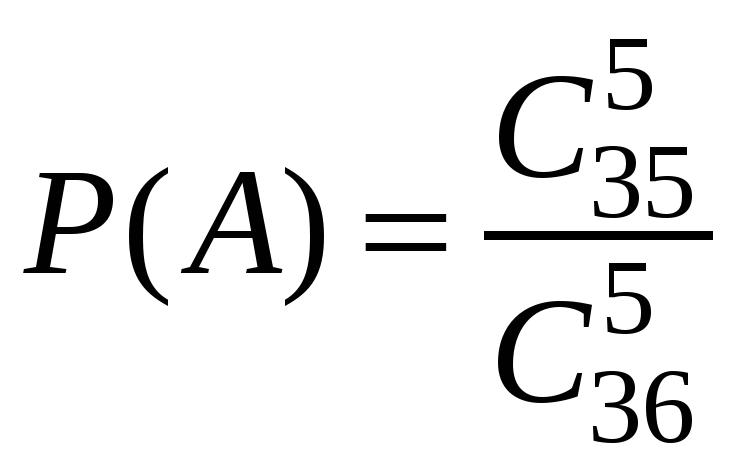

вероятность «неудачи» .

Подведение итогов

Для числа сочетаний из n по k

справедлива формула

Например:

Вероятностью события А, связанного с некоторым опытом называют отношение числа благоприятных исходов N(А) ( в результате которых наступает событие А ) к общему числу N всех элементарных равновозможных между собой исходов этого опыта.

Для нахождения вероятности события А при проведении некоторого опыта следует:

1) найти число N всех возможных исходов данного опыта;

2) принять предложение о равновозможности всех этих исходов;

3) Найти количество N ( А ) тех исходов опыта, в которых наступает событие А ;

4) Найти частное ; оно и будет вероятностью события А .

• Производится серия n независимых испытаний.
• У каждого испытания 2 исхода: A - "успех" и - "неуспех".
• Вероятность "успеха" в каждом испытании одинакова и равна P( A ) = p (соответственно, вероятность "неуспеха" также не меняется от опыта к опыту и равна ).

Какова вероятность того, что в серии из n опытов k раз наступит успех? Найти .

• Вероятность наступления ровно k успехов в n независимых повторениях одного и того же испытания находится по формуле

,

где p – вероятность «успеха»,

q = 1- p - вероятность «неудачи» в отдельном опыте.

«Что ни толкуй Вольтер или Декарт – Мир для меня колода карт, Жизнь – банк; рок мечет, я играю, И правила игры я к людям применяю». М.Ю. Лермонтов

В коробке лежат 3 красных и 5 синих шариков. Какое наименьшее количество шариков, не глядя, нужно достать из коробки, чтобы среди них обязательно оказалось хотя бы 2 шарика одного цвета?

События

результаты испытаний, опытов

случайные

достоверные

невозможные

могут произойти, а могут не произойти

никогда не произойдут

обязательно произойдут

Предметом изучения теории вероятностей являются закономерности , которым подчиняются случайные события при многократном повторении опыта в одних и тех же условиях.

Задача Д , аламбера

Брошены две монеты. Какова вероятность того, что обе выпадут гербом кверху?

Свойства вероятности

1.0

2. P(U) = 1 , т.к. m=n

3. P(V) = 0, т.к. m=0

Задача

В доме100 квартир. Наугад выбирается одна из них. Какова вероятность того, что на двери выбранной квартиры вы увидите цифру «5»?

Блез Паскаль

1623-1662

Пьер Ферма

1601-1665