Муниципальное бюджетное общеобразовательное учреждение
«Гимназия №1 п. Навля»
СОГЛАСОВАНО
Председатель методического Совета
_______________ /Чубакова Н. А./
УТВЕРЖДАЮ
Директор гимназии
________________/Изотова С. А./
Приказ № ______ от ____. _____. 2015 г.
Рабочая программа
повышенного уровня сложности
по математике
для 8 класса
Составитель: Кряжкова Л. А., учитель математики
Год составления программы – 2015.
Рассмотрена и рекомендована к утверждению методическим советом МБОУ «Гимназия № 1 п. Навля».
Протокол №______ от ____._____. 2015 г.
Пояснительная записка.
Сведения об учебной программе.
Рабочая программа повышенного уровня сложности разработана на основе: компонента федерального Государственного стандарта, примерной программы основного общего образования по математике, программы по математике для 8 класса общеобразовательных учреждений под редакцией А.Г. Мордковича изд. Мнемозина М, 2009 г. и на основе авторской программы курса геометрии для 8 класса общеобразовательных учреждений под редакцией Л.С. Атанасяна изд. «Просвещение» М. 2009, и включающей в себя материал, отражающий содержание примерной программы, и дополнена гимназическим компонентом по содержанию.
2. Описание места учебного предмета, курса в учебном плане.
В соответствии с учебным планом МБОУ «Гимназия №1 п. Навля» на изучение математики в 8 классе отводится 175 часов. Рабочая программа предусматривает обучение математики в объеме 5-ти часов в неделю в течение одного учебного года.
Общие цели и задачи ступени образования с учетом специфики учебного предмета.
Изучение математики на ступени основного общего образования направлено на достижение следующих целей:
Овладение системой математических знаний и умений в соответствии с требованиями федерального компонента Государственного образовательного стандарта основного общего образования по математике и повышенного уровня сложности данной программы, необходимых для применений в практической деятельности, изучении смежных дисциплин, продолжения образования;
Интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе, свойственных математической деятельности: ясность и точность мысли, критичность мышления, интуиция, логическое мышление, элементы алгоритмической культуры, пространственных представлений, способность к преодолению трудностей;
Формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;
Воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, играющей особую роль в общественном развитии.
4. Общая характеристика учебного предмета, курса.
Математическое образование в основной школе складывается из следующих содержательных компонентов (точные названия блоков): арифметика; алгебра; геометрия; элементы комбинаторики, теории вероятностей, статистики и логики. В своей совокупности они отражают богатый опыт обучения математике в нашей стране, учитывают современные тенденции отечественной и зарубежной школы и позволяют реализовать поставленные перед школьным образованием цели на информационно емком и практически значимом материале. Эти содержательные компоненты, развиваясь на протяжении всех лет обучения, естественным образом переплетаются и взаимодействуют в учебных курсах.
Арифметика призвана способствовать приобретению практических навыков, необходимых для повседневной жизни. Она служит базой для всего дальнейшего изучения математики, способствует логическому развитию и формированию умения пользоваться алгоритмами.
Алгебра нацелена на формирование математического аппарата для решения задач из математики, смежных предметов, окружающей реальности. Язык алгебры подчеркивает значение математики как языка для построения математических моделей, процессов и явлений реального мира. Одной из основных задач изучения алгебры является развитие алгоритмического мышления, необходимого, в частности, для освоения курса информатики; овладение навыками дедуктивных рассуждений. Преобразование символических форм вносит свой специфический вклад в развитие воображения, способностей к математическому творчеству. Другой важной задачей изучения алгебры является получение школьниками конкретных знаний о функциях как важнейшей математической модели для описания и исследования разнообразных процессов (равномерных, равноускоренных, экспоненциальных, периодических и др.), для формирования у учащихся представлений о роли математики в развитии цивилизации и культуры.
Геометрия — один из важнейших компонентов математического образования, необходимый для приобретения конкретных знаний о пространстве и практически значимых умений, формирования языка описания объектов окружающего мира, для развития пространственного воображения и интуиции, математической культуры, для эстетического воспитания учащихся. Изучение геометрии вносит вклад в развитие логического мышления, в формирование понятия доказательства.
Таким образом, в ходе освоения содержания курса учащиеся получают возможность:
- развить представления о числе и роли вычислений в человеческой практике; сформировать практические навыки выполнения устных, письменных, инструментальных вычислений, развить вычислительную культуру;
- овладеть символическим языком алгебры, выработать формально-оперативные алгебраические умения и научиться применять их к решению математических и нематематических задач;
- изучить свойства и графики элементарных функций, научиться использовать функционально-графические представления для описания и анализа реальных зависимостей;
- развить пространственные представления и изобразительные умения, освоить основные факты и методы планиметрии, познакомиться с простейшими пространственными телами и их свойствами;
- развить логическое мышление и речь — умения логически обосновывать суждения, проводить несложные систематизации, приводить примеры и контр примеры, использовать различные языки математики (словесный, символический, графический) для иллюстрации, интерпретации, аргументации и доказательства;
- сформировать представления об изучаемых понятиях и методах как важнейших средствах математического моделирования реальных процессов и явлений.
5. Требования к подготовке выпускников основного общего образования:
В результате изучения математики 8 класса учащиеся должны знать (понимать):
► развитие числа, введение в математику новых чисел обусловлено потребностями практики, а также внутренними потребностями математики;
►различать алгебраические дроби среди других буквенных выражений;
►понятие квадратного корня и его свойства;
►виды изученных функций, их свойства, способы задания и графики;
►выделять среди выражений квадратный трехчлен и знать формулу его разложения;
►квадратное уравнение и формулы его корней; рациональное уравнение; иррациональное уравнение; биквадратное уравнение;
►виды неравенств и методы их решения(алгоритмы) как их использовать для решения математических и практических задач;
►понятие многоугольника и его виды.
►определение параллелограмма, трапеции, прямоугольника, ромба, квадрата и их свойства и формулы для нахождения площадей
►теорему Пифагора.
►определение подобных треугольников и их признаки; Отношение площадей подобных треугольников.
►средняя линия треугольника и ее свойство.
►определение синуса, косинуса и тангенса острого угла прямоугольного треугольника.
►касательная к окружности.
►центральные и вписанные углы и их свойства.
►вписанная и описанная окружности и их свойства.
►как использовать математические формулы; примеры их применения для решения математических и практических задач
В результате изучения математики 8 класса учащиеся должны уметь:
►применять основное свойство алгебраической дроби для сокращения дробей; находить сумму, разность, произведение и частное двух алгебраических дробей; выполнять тождественные преобразования несложных алгебраических выражений, содержащих многочлены и алгебраические дроби;
►находить квадратный корень из числа, являющегося квадратом одного из первых двадцати натуральных чисел, выносить множитель из-под знака корня и вносить, сравнивать иррациональные числа, применять свойства квадратных корней для упрощения числовых выражений;
►уметь решать изученные виды неравенств;
►понимать смысл требования «решить уравнение», использовать подстановку для проверки того, является ли данное число корнем уравнения; распознавать уравнения первой и второй степени с одним неизвестным; решать уравнения первой и второй степени с одним неизвестным.
►методом составления уравнения решать текстовые задачи,
приводящие к указанным уравнениям; решать несложные рациональные уравнения, сводящиеся к решению уравнения первой или второй степени; методом составления уравнения решать текстовые задачи, приводящие к несложным рациональным уравнениям.
►понимать смысл требования «решить неравенство», использовать подстановку для проверки того, является ли данное число решением неравенства с одним неизвестным; решать линейные и квадратные неравенства с одним неизвестным.
►исследовать числовые функции по графику и аналитически; различать числовые функции и их графики; строить графики по таблице и методом преобразований (сложных преобразований, по исследованию функции);
►задавать функцию по графику, условию, по таблице;
►уметь представлять подкоренное выражение в виде полного квадрата и применять тождество√а2=│а│.
►решать уравнения, сводящиеся к квадратным.
►решать несложные иррациональные неравенства.
►находить площади четырехугольников изучаемых в 8 классе.
►применять теорему Пифагора при решении задач
►распознавать плоские геометрические фигуры, различать их взаимное расположение, аргументировать суждения, используя определения, свойства, признаки;
►изображать планиметрические фигуры; выполнять чертежи по условию задач;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
►описания реальных ситуаций на языке геометрии;
►расчетов, включающих простейшие тригонометрические формулы
►решение практических задач, связанных с нахождением геометрических величин
6. Содержание учебного материала обозначенные в темах и разделах, включая элементы обязательного минимума образования, гимназический компонент.
Содержание данной рабочей программы состоит из содержания, определенного требованиями Федерального компонента государственного стандарта основного общего образования по математике, примерной программы по математике, гимназическим компонентом по содержанию, введенным за счет углубления содержания примерной программы содержанием авторской программы по алгебре под редакцией А.Г. Мордковича изд. Мнемозина. и по геометрии под редакцией Л.С. Атанасяна изд. Просвещение
Содержание рабочей программы.
| Наимено-вание раздела | Название темы | Содержание учебного материала | Требования к уровню подготовки учащихся |
| Алгебраические дроби. | 1 .Основные понятия. | Алгебраическая дробь. Допустимые значения. | Знать/понимать: - основное свойство дроби; - правила сложения и вычитания дробей с одинаковыми и разными знаменателями; - правила умножения и деления дробей; - рациональное выражение, рациональное уравнение; - степень с целым отрицательным показателем. Уметь: -уметь находить допустимые значения переменной; -уметь сокращать дроби после разложения на множители числителя и знаменателя; - выполнять действия с алгебраическими дробями; - упрощать выражения с алгебраическими дробями; - решать простейшие рациональные уравнения; - выполнять действия со степенями с отрицательными целыми показателями. |
| 2. Основное свойство алгебраической дроби. | Основное свойство дроби, сокращение дробей, тождественные преобразования. |
| 3. Сложение и вычитание алгебраических дробей с одинаковыми знаменателями. | Сложение и вычитание дробей с одинаковыми знаменателями |
| 4. Сложение и вычитание алгебраических дробей с разными знаменателями. | Сложение и вычитание дробей с разными знаменателями |
| 5. Умножение и деление алгебраических дробей. Возведение алгебраической дроби в степень. | Правило умножения дробей, возведение дробей в степень. Правило деления дробей. |
| 6. Преобразование рациональных выражений. | Рациональное выражение, сложение, вычитание, умножение, деление рациональных дробей. |
| 7. Первые представления о рациональных уравнениях. | Рациональное уравнение. Правило решения рациональных уравнений. |
| 8. Степень с отрицательным целым показателем | Определение степени с отрицательным целым показателем, свойства степени. |
| Контрольные работы № 1,2 |
| Уметь применять изученный теоретический материал при выполнении письменной работы |
|
Функ-ция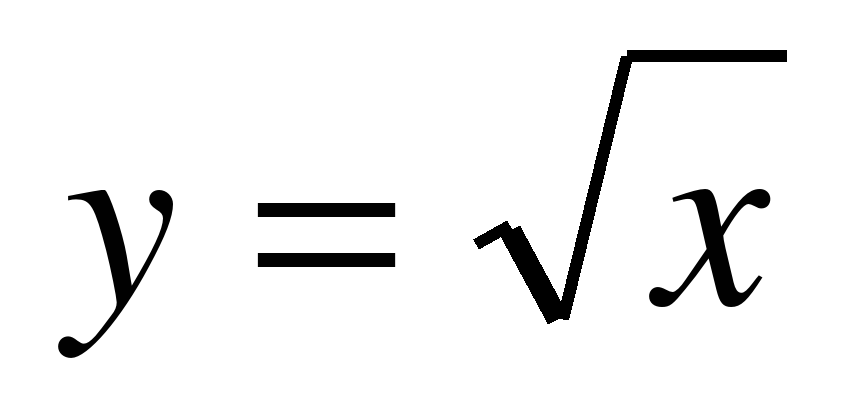 Свой-ства квад-рат-ного корня. Свой-ства квад-рат-ного корня.
| 9. Рациональные числа | Множество рациональных чисел, бесконечные десятичные периодические дроби, период, чисто периодическая дробь, смешанно периодическая дробью | Знать/понимать: - рациональные числа, бесконечная десятичная периодическая дробь; - действительные и иррациональные числа; - о делимости целых чисел, о делении с остатком; - определение арифметического квадратного корня; - свойства арифметического квадратного корня; - определение модуля действительного числа. Уметь: - извлекать квадратные корни из неотрицательного числа; - применять свойства арифметического квадратного корня к преобразованию выражений; - вычислять значения выражений, содержащих квадратные корни; - освобождаться от иррациональности в знаменателе; - исследовать уравнение 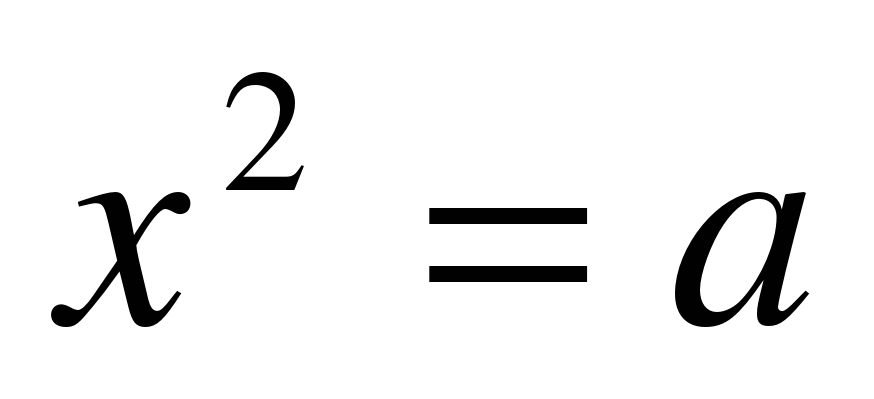 ; ; - строить график функции 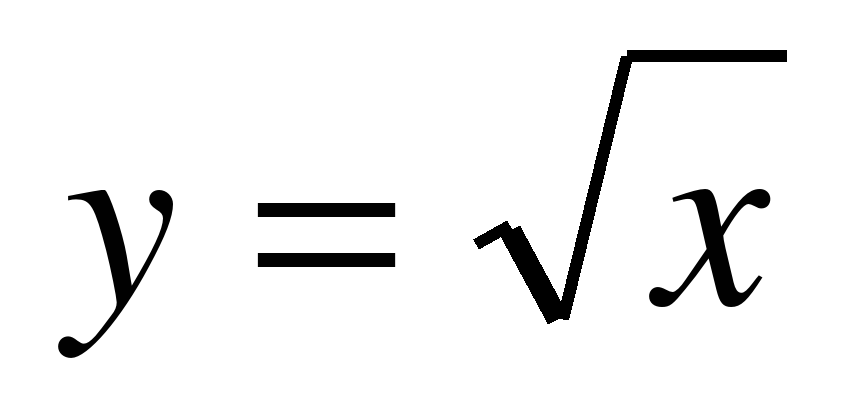 и работать с ним; и работать с ним; - применять свойства модуля.
|
| 10. Понятие квадратного корня из неотрицательного числа. | Квадратные корни. Арифметический квадратный корень. Уравнение 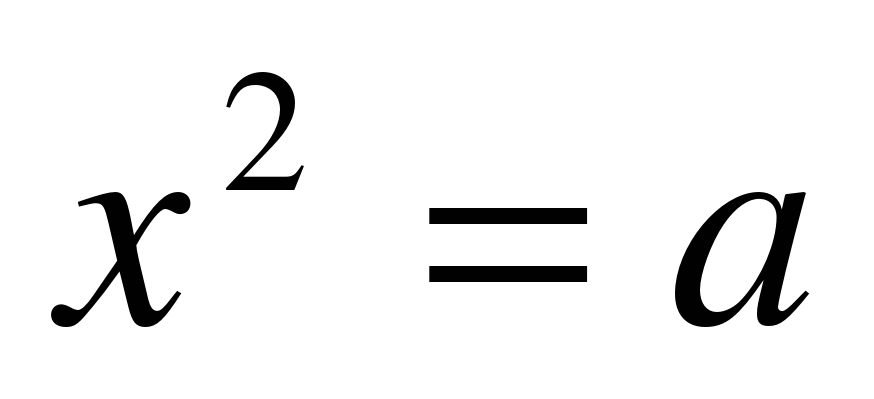 . Нахождение приближенных значений квадратного корня. Выделение полного квадрата в квадратном трехчлене. . Нахождение приближенных значений квадратного корня. Выделение полного квадрата в квадратном трехчлене. |
| 11. Иррациональные числа. | Иррациональные числа, бесконечная десятичная непериодическая дробь, иррациональные выражения |
| 12. Множество действительных чисел | Множество действительных чисел, сравнение действительных чисел, арифметические действия над действительными числами. |
| 13. Функция 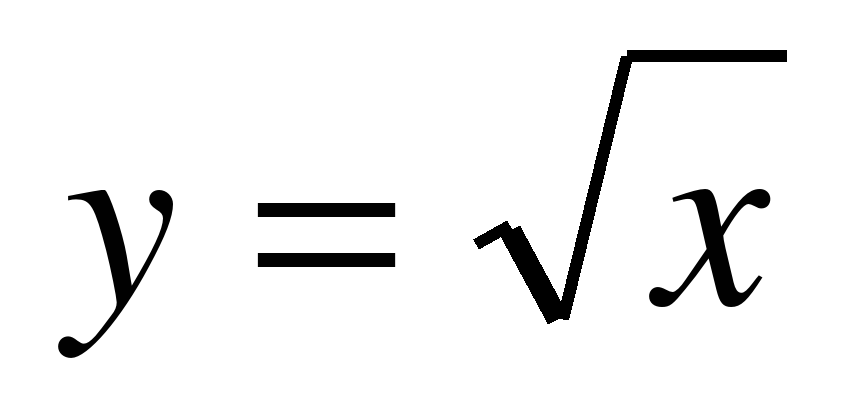 , ее свойства и график. , ее свойства и график. | График функции, свойства функции. |
| 14. Свойства квадратных корней. | Квадратный корень из произведения, квадратный корень из дроби,
вычисление корней |
| 15. Преобразование выражений, содержащих операцию извлечения квадратного корня. | Преобразование выражений, содержащих операцию извлечения квадратного корня, освобождение от иррациональности в знаменателе |
| 16. Модуль действительного числа. | Модуль действительного числа, свойства модулей, геометрический смысл модуля действительного |
| Контрольная работа № 3. |
| Уметь применять изученный теоретический материал при выполнении письменной работы |
|
Квад-ратичная функция. Функция 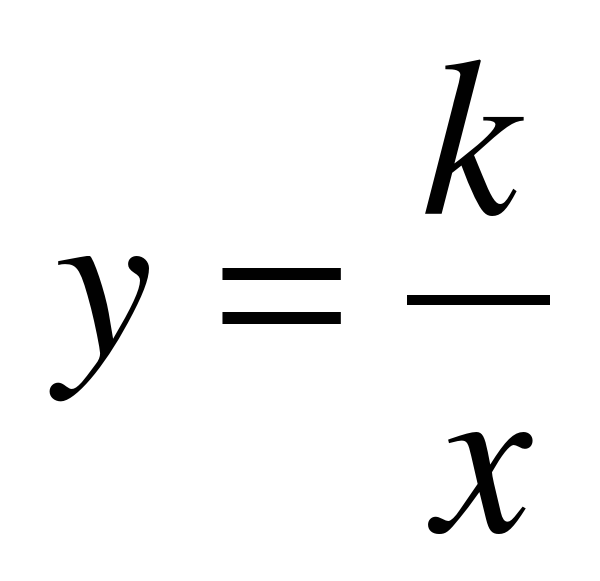 . . | 17. Функция  , ее свойства и график. , ее свойства и график. | Кусочные функции, контрольные точки графика, функция y = kx2, ее свойства и график. | Знать/понимать: - о функциях вида y = kx2 и 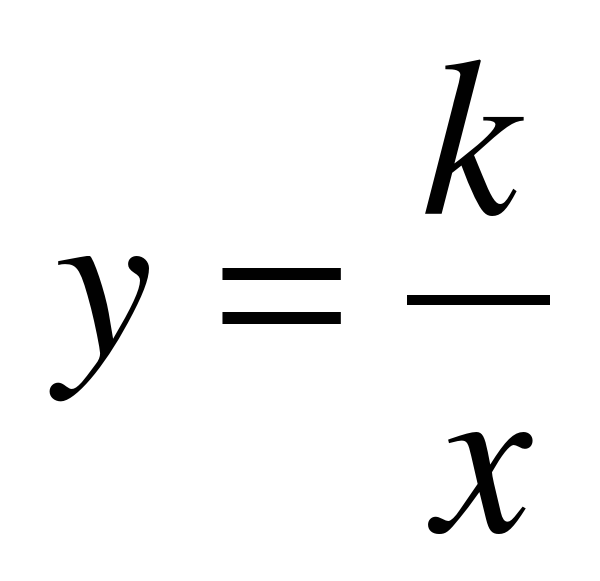 , , y = ax2 + bx + c , о их графиках и свойствах; - как с помощью параллельного переноса построить графики функций y = f(x + l), y = f(x) + m, y = f(x + l) + m; - алгоритм построения параболы y = ax2 + bx + c; - графические способы решения квадратных уравнений. Уметь: - строить графики функций y = kx2, 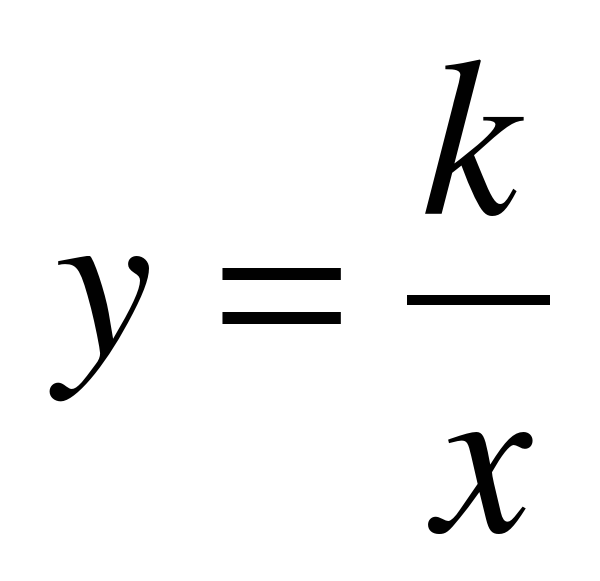 , , y = ax2 + bx + c , y = f(x + l), y = f(x) + m, y = f(x + l) + m; - описывать свойства функций по ее графику; - решать графически квадратные уравнения. |
| 18. Функция 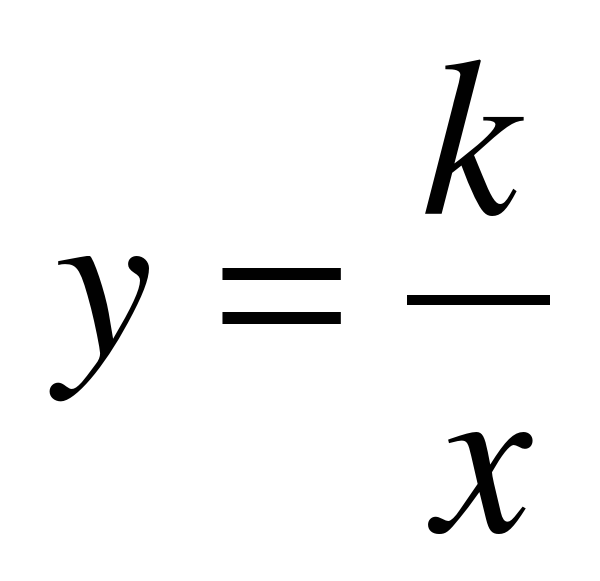 , ее свойства и график. , ее свойства и график. | Функция 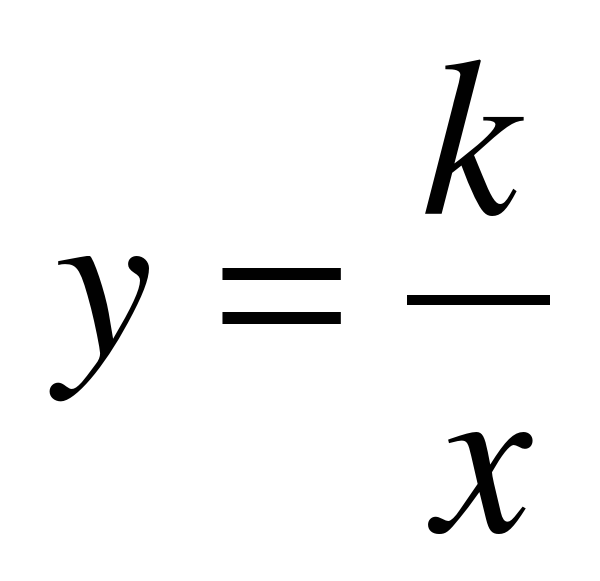 , ее свойства и график при различных значения k. , ее свойства и график при различных значения k. |
| 19. Как построить график функции  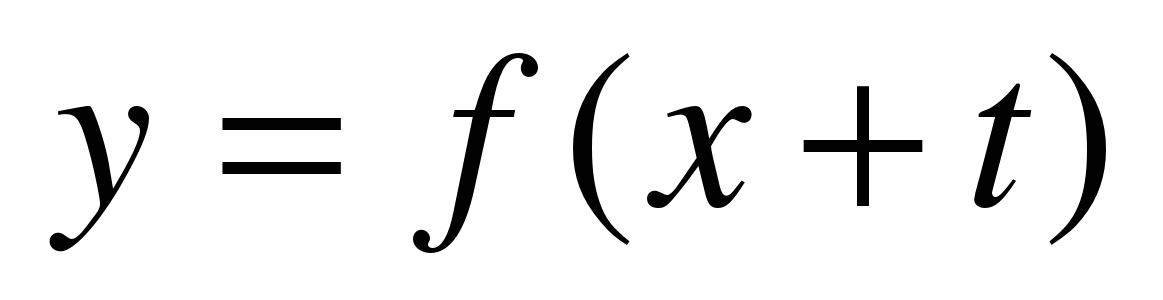 , если известен график функции , если известен график функции  . . | Параллельный перенос вправо (влево), вспомогательная система координат, алгоритм построения графика функции
y = f(x + l). |
| 20. Как построить график функции 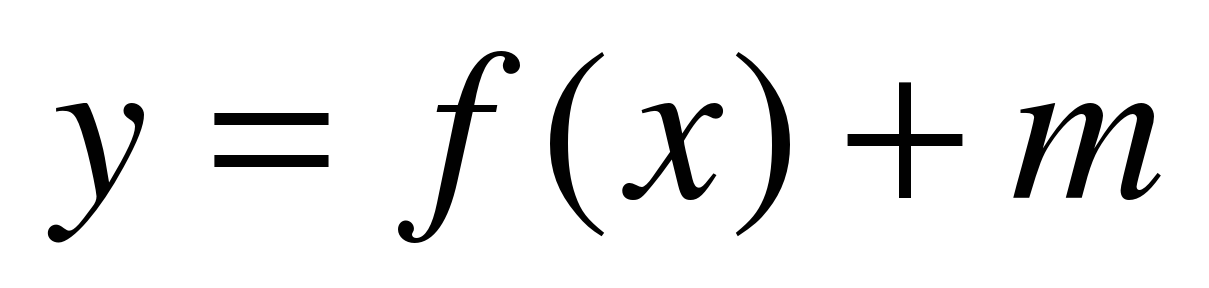 , если известен график функции , если известен график функции  . . | Параллельный перенос вверх (вниз), вспомогательная система координат, алгоритм построения графика функции
y = f(x) + m |
| 21. Как построить график функции 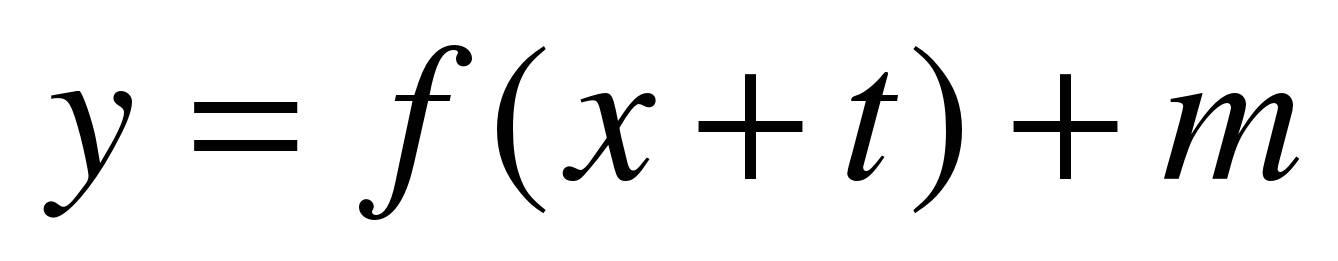 , если известен график функции , если известен график функции  . . | Параллельный перенос вправо (влево), параллельный перенос вверх (вниз), вспомогательная система координат, алгоритм построения графика функции
y = f(x + l) + m. Симметрия графиков относительно осей координат. |
| 22. Функция 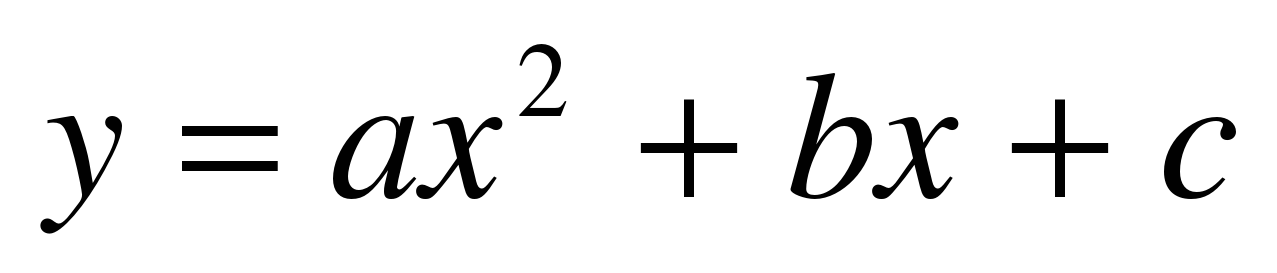 , ее свойства и график. , ее свойства и график. | Функция y = ax2 + bx + c,
квадратичная функция, график квадратичной функции, координаты вершины параболы, алгоритм построения параболы y = ax2 + bx + c |
| 23. Графическое решение квадратных уравнений. | Квадратное уравнение, несколько способов графического решения уравнения. |
| Контрольные работы № 4, 5 |
| Уметь применять изученный теоретический материал при выполнении письменной работы |
| Квадратные уравнения. | 24. Основные понятия. | Квадратное уравнение, приведенное квадратное уравнение, полное квадратное уравнение, неполное квадратное уравнение, корень квадратного уравнения, решение квадратного уравнения. | Знать/понимать: - квадратные и дробные уравнения; - способы решения неполных квадратных уравнений; - формулу корней квадратного уравнения; - теорему Виета; - иррациональные уравнения и способы их решения. Уметь: - решать квадратные уравнения, а также уравнения сводящиеся к ним; - решать дробно-рациональные уравнения; - исследовать квадратное уравнение по дискриминанту и коэффициентам; - решать текстовые задачи с помощью квадратных и дробно-рациональных уравнений; - решать иррациональные уравнения. |
| 25. Формула корней квадратных уравнений. | Дискриминант квадратного уравнения, формула корней квадратного уравнения. |
| 26. Рациональные уравнения. | Рациональные уравнения, алгоритм решения рационального уравнения, проверка корней уравнения, посторонние корни |
| 27. Рациональные уравнения как математические модели реальных ситуаций. | Рациональные уравнения, математическая модель реальной ситуации, решение задач на составление уравнений. |
| 28. Еще одна формула корней квадратного уравнения. | Квадратное уравнение с четным вторым коэффициентом, формула корней квадратного уравнения с четным вторым коэффициентом. |
| 29. Теорема Виета. | Теорема Виета, обратная теорема Виета, симметрическое выражение с двумя переменными. |
| 30. Иррациональные уравнения. | Иррациональные уравнения, метод возведения в квадрат, проверка корней, равносильные уравнения, равносильные преобразования уравнения, неравносильные преобразования уравнения. |
|
| Контрольные работы № 6, 7 |
| Уметь применять изученный теоретический материал при выполнении письменной работы |
| Неравенст-ва. | 31. Свойства числовых неравенств. | Числовое неравенство, свойства числовых неравенств, неравенства одинакового смысла, неравенства противоположного смысла, среднее арифметическое, среднее геометрическое, неравенство Коши | Знать/понимать: - определение числового неравенства4 - свойства числовых неравенств; - стандартный вид числа; - возрастание, убывание функций.
Уметь: - находить пересечение и объединение множеств; - иллюстрировать на координатной прямой числовые неравенства; - применять свойства числовых неравенств при решении задач; - решать линейные неравенства; - решать квадратные неравенства разными способами; - находить промежутки возрастания и убывания функций; - записывать числа в стандартном виде.
|
| 32. Исследование функций на монотонность. | Возрастающая функция на промежутке, убывающая функция на промежутке, монотонная функция. |
| 33. Решение линейных неравенств. | Неравенство с переменной, решение неравенства с переменной, множество решений, система линейных неравенств, пересечение решений неравенств системы. |
| 34. Решение квадратных неравенств. | Квадратное неравенство, знак объединения множеств, алгоритм решения квадратного неравенства, метод интервалов. Доказательство числовых и алгебраических неравенств. |
| 35. Приближенные значения действительных чисел. | Приближенное значение по недостатку, приближенное значение по избытку, округление чисел, погрешность приближения, абсолютная и относительная погрешности. |
| 36. Стандартный вид положительного числа. | Стандартный вид положительного числа, порядок числа, запись числа в стандартной форме. |
| Контрольная работа № 8 |
| Уметь применять изученный теоретический материал при выполнении письменной работы
|
|
Четырех-угольники | 1.Многоугольники. | Многоугольники. Выпуклые многоугольники. Сумма углов выпуклого многоугольника. | Знать/понимать: - Определения: многоугольника, параллелограмма, трапеции, прямоугольника, ромба, квадрата; - формулу суммы углов выпуклого многоугольника; - свойства этих четырехугольников; - признаки параллелограмма; - виды симметрии. Уметь: - распознавать на чертеже многоугольники и выпуклые многоугольники; параллелограммы и трапеции; - применять формулу суммы углов выпуклого многоугольника; - применять свойства и признаки параллелограммов при решении задач; - делить отрезок на n равных частей; - строить симметричные точки и распознавать фигуры, обладающие осевой и центральной симметрией; - выполнять чертеж по условию задачи. |
| 2.Параллелограмм и трапеция. | Параллелограмм и его свойства. Признаки параллелограмма. Трапеция, Средняя линия трапеции. Равнобедренная трапеция и ее свойства. Теорема Фалеса. Задачи на построение. |
| 3.Прямоуголник, ромб, квадрат. | Прямоугольник и его свойства. Ромб, квадрат их свойства и признаки. Осевая и центральная симметрия, как свойства геометрических фигур. |
| Контрольная работа. № 1. |
| Уметь применять изученный теоретический материал при выполнении письменной работы |
| Площадь | 1.Площадь многоугольника. | Понятие о площади. Равновеликие фигуры. Свойства площадей. | Знать/понимать: - представление о способе измерения площади, свойства площадей; - формулы площадей: прямоугольника, параллелограмма, треугольника, трапеции; - формулировку теоремы Пифагора и обратной ей. Уметь: - находить площади прямоугольника, параллелограмма, треугольника, трапеции; - применять формулы при решении задач; - находить стороны треугольника, используя теорему Пифагора; - определять вид треугольника, используя теорему, обратную теореме Пифагора. - выполнять чертеж по условию задачи. |
| 2.Площадь параллелограмма, трапеции, треугольника. | Формулы площадей прямоугольника, параллелограмма, треугольника, трапеции. Теорема об отношении площадей треугольников имеющих по равному углу. Формула Герона. Площадь четырехугольника. |
| 3.Теорема Пифагора. | Теорема Пифагора и теорема обратная теореме Пифагора. |
| Контрольная работа № 2 |
| Уметь применять изученный теоретический материал при выполнении письменной работы |
| Подобные треуголь-ники.
| 1.Определение подобных треугольников.
| Подобие треугольников. Коэффициент подобия. Связь между площадями подобных фигур. | Знать/понимать: - определение подобных треугольников; - формулировки признаков подобия треугольников; - формулировку теоремы об отношении площадей подобных треугольников; - формулировку теоремы о средней линии треугольника; - свойство медиан треугольника; -понятие среднего пропорционального, - свойство высоты прямоугольного треугольника, проведенной из вершины прямого угла; - определение синуса, косинуса, тангенса острого угла прямоугольного треугольника - значения синуса, косинуса, тангенса углов 30º, 45º, 60º, 90º. Уметь: - находить элементы треугольников, используя определение подобных треугольников; - находить отношение площадей подобных треугольников; - применять признаки подобия при решении задач; - применять метод подобия при решении задач на построение; - находить значение одной из тригонометрических функций по значению другой; - решать прямоугольные треугольники. |
| 2.Признаки подобия треугольников. | Три признака подобия треугольников.
|
| 3.Применение подобия к доказательству теорем и решению задач. | Средняя линия треугольника. Свойство медиан треугольника. Среднее пропорциональное. Пропорциональные отрезки в прямоугольном треугольнике. Измерительные работы на местности. Метод подобия. |
| 4.Соотношения между сторонами и углами прямоугольного треугольника. | Понятия синуса, косинуса, тангенса острого угла прямоугольного треугольника. Основное тригонометрическое тождество. Значения синуса, косинуса, тангенса углов 30º, 45º, 60º, 90º. |
|
Контрольная работа № 3,4 |
| Уметь применять изученный теоретический материал при выполнении письменной работы. |
| Окружность.
| 1.Касательная и окружность. | Взаимное расположение прямой и окружности. Касательная и секущая к окружности. Точка касания. Свойство касательной и признак. Взаимное расположение двух окружностей. | Знать/понимать: - случаи взаимного расположения прямой и окружности; - понятие касательной, точек касания, свойство касательной; - определение вписанного и центрального углов; - определение серединного перпендикуляра; - формулировку теоремы об отрезках пересекающихся хорд; - четыре замечательные точки треугольника; - определение вписанной и описанной окружностей. Уметь: - определять и изображать взаимное расположение прямой и окружности; - окружности, вписанные в многоугольник и описанные около него; - распознавать и изображать центральные и вписанные углы; - находить величину центрального и вписанного углов; - применять свойства вписанного и описанного четырехугольника при решении задач; - выполнять чертеж по условию задачи; - решать простейшие задачи, опираясь на изученные свойства. |
| 2.Центроальные и вписанные углы. | Центральные и вписанные углы. Градусная мера дуги окружности. Теорема о вписанном угле и следствия из нее. Теорема об отрезках пересекающихся хорд. Метрические соотношения в окружности: свойства секущих, касательных, хорд. |
| 3.Четыре замечательные точки треугольника. | Теорема о свойстве угла биссектрисы. Серединный перпендикуляр. Теорема о серединном перпендикуляре. Теорема о точке пересечения высот треугольника. |
| 4.Вписанная и описанная окружности. | Вписанная и описанная окружности. Теорема об окружности, вписанной в треугольник. Теорема об окружности, описанной около треугольника. Свойства вписанного и описанного четырехугольника. Вписанные и описанные четырехугольники. |
| Контрольная работа. |
| Уметь применять изученный теоретический материал при выполнении письменной работы |
| Повто-рение. | Алгебра.
| Действия с рациональными дробями. Действия с корнями. Решение квадратных и рациональных уравнений. Решение задач с помощью квадратных и рациональных уравнений. Решение неравенств. |
|
| Геометрия. | Решение задач по всему курсу. Примеры движений фигур. Симметрия фигур. Осевая и центральная симметрии. Понятие о гомометрии. Подобие фигур. |
|
7. Учебно - тематический план.
| Тематика разделов (глав, параграфов) | Кол-во часов, отводимое на эту тему | Кол-во к/р, зачетов, итогов.срезов | Кол-во практи-ческих занятий (работ) | Кол-во творч. работ (проектов) |
| Алгебраические дроби Рациональные уравнения | 21 | 2к.р. 1зачет |
|
|
| Функция y=√x. Свойства квадратного корня. Модуль и иррациональность в решении задач | 18 | 1к..р.
|
|
|
| Квадратичная функция. Функция y=k/x. Построение и чтение графиков кусочных функций. | 18 | 2к.р. 1зачет | 2 | 5 |
| Квадратные уравнения. Уравнения, сводящиеся к квадратным Параметр. Уравнение с параметром. | 24 | 2к.р. 1зачет |
|
|
| Неравенства. Иррациональные неравенства. | 14
| 1к.р 1зачет |
|
|
| Четырехугольники | 14 | 1к.р 1зачет | 1 | 1 |
| Площадь | 13 | 1к.р. 1зачет | 1 | 1 |
| Подобные треугольники | 19 | 1к.р 1зачет |
| 1 |
| Окружность | 14 | 1к.р.
| 1 |
|
| Обобщающее повторение. | 20 | 1к.р тест |
|
|
| Итого в год. | 175 | 13к.р 8 зачетов | 5 | 8 |
Выделенные темы и часы являются гимназическим компонентом.
8. Способы проверки знаний учащихся.
Контроль знаний, умений и навыков учащихся - важнейший этап учебного процесса, выполняющий обучающую, проверочную, воспитательную и корректирующую функции. Для контроля уровня достижений учащихся используются такие виды контроля как:
предварительный,
текущий,
тематический,
итоговый контроль;
формы контроля:
контрольная работа,
дифференцированный индивидуальный письменный опрос,
самостоятельная проверочная работа,
тестирование,
диктант,
письменные домашние задания,
анализ творческих, исследовательских работ, результатов выполнения диагностических заданий учебного пособия или рабочей тетради.
Результаты обучения учебного года с учетом гимназического компонента.
АЛГЕБРА. В результате изучения темы учащийся должен
Знать/понимать:
- основные свойства функций;
- общие методы решения уравнений и неравенств;
Уметь:
- находить значения алгебраических дробей, область допустимых значений для дробей;
- составлять математические модели для задач;
- сокращать дроби, выполнять арифметические действия с алгебраическими дробями;
- возводить дробь в степень;
- упрощать выражения, доказывать тождества;
- решать рациональные, квадратные, биквадратные, иррациональные уравнения;
- находить значения функции, заданной формулой, таблицей, графиком по ее аргументу; находить значение аргумента по значению функции, заданной графиком или таблицей;
- определять свойства функции по ее графику; применять графические представления при решении уравнений, систем, неравенств;
- описывать свойства изученных функций, строить их графики, строить графики функций с помощью параллельного переноса;
- решать уравнения графически;
- вычислять квадратный корень из чисел и выражений, используя свойства;
- выносить/вносить множитель из-под корня;
- переводить периодические дроби в обыкновенные;
- находить значение выражения с модулем;
- работать со степенями с отрицательным показателем;
- уметь приводить число к стандартному виду;
- раскладывать квадратный трехчлен на множители;
- пользоваться свойствами числовых неравенств;
- решать линейные и квадратные неравенства.
Гимназический компонент:
- уметь сокращать дроби при построении графиков функций;
- уметь преобразовывать дроби при доказательстве тождеств;
- иметь представление о рациональных уравнениях;
- строить графики функций с помощью параллельного переноса;
- уметь построить и прочитать график кусочной функции;
- уметь пользоваться модулем и иррациональностью при решение сложных задач;
- уметь сравнивать действительные числа и выполнять арифметические действия над ними;
- уметь выделять полный квадрат в квадратном трехчлене;
- уметь решать уравнения с параметром;
- уметь решать задачи путем введения новой переменной;
- уметь решать уравнения, сводимые к квадратным;
- уметь доказывать числовые и алгебраические неравенства;
- иметь представление о решении иррациональных неравенств.
ГЕОМЕТРИЯ.
Знать/понимать:
- формулу суммы углов выпуклого многоугольника;
- понятие и свойства равнобедренной и прямоугольной трапеции;
- понятия параллелограмма, прямоугольника, ромба и квадрата, их свойства и признаки;
- формулы для вычисления площади прямоугольника, параллелограмма, треугольника и трапеции;
- теорему об отношении площадей треугольников, имеющих по равному углу;
- теорему Пифагора;
- признаки подобия треугольников;
- теоремы о средней линии и пропорциональных отрезках в прямоугольном треугольнике;
- основное тригонометрическое тождество;
- теорему о вписанном угле, следствия из нее;
- теорему о произведении отрезков пересекающихся хорд;
- теорему об окружности, вписанной в многоугольник, и окружности, описанной около многоугольника;
- свойства вписанного и описанного четырехугольника;
Уметь:
- выводить и пользоваться формулой суммы углов выпуклого многоугольника;
- доказывать и применять свойства и признаки параллелограмма, трапеции, прямоугольника, ромба и квадрата при решении задач;
- выполнять чертежи по условию задачи;
- делить отрезок на n равных частей, в данном отношении с помощью циркуля и линейки;
- решать задачи на построение;
- строить симметричные точки, распознавать фигуры, обладающие осевой и центральной симметрией;
- выводить и использовать формулу площади прямоугольника, параллелограмма, треугольника и трапеции;
- применять все изученные формулы и теоремы при решении задач, проводя аргументацию в ходе решения задач;
- доказывать подобие треугольников с использованием соответствующих признаков;
- вычислять элементы подобных треугольников.
Гимназический компонент:
- уметь доказывать теорему Фалеса;
- знать формулу Герона;
- уметь вычислять площади с помощью различных формул;
- уметь применять теорему Пифагора при решении сложных задач;
- знать и уметь применять свойства «четырех замечательных точек треугольника».
10. Ресурсное обеспечение рабочей программы
| № п\п | Наименование авторской программы, уч. пособия, дидактического материала, уч. тетради, сборников методических рекомендаций (но не поурочного планирования) и т.д. | Автор | Издательство | Год издания |
| 1. | Программа по алгебре для общеобразовательной школы | А.Г. Мордкович | Мнемозина | Москва 2009 |
| 2. | Учебник. Алгебра 8 | А.Г. Мордкович | Мнемозина | Москва 2010 |
| 3. | Задачник. Алгебра 8 | А.Г. Мордкович | Мнемозина | Москва 2010 |
| 4. | Алгебра. Самостоятельные работы для 8 класса. | Л.А. Александрова | Мнемозина | Москва 2008 |
| 5. | Алгебра. Контрольные работы для 8 класса. | Л.А. Александрова | Мнемозина | Москва 2008 |
| 6. | Тесты для промежуточной аттестации 7-8 классы | Ф.Ф. Лысенко | Легион | Ростов-на Дону 2013 |
| 7. | Алгебра. Математические диктанты 7-9 классы | А.С. Конте | Учитель | Волгоград 2007 |
| 8. | Алгебра: Сборник заданий для подготовки к итоговой аттестации в 9 классе | Л.В. Кузнецова и др. | Просвещение | Москва 2008 |
| 9 | Алгебра. 7-9 для учащихся общеобразовательных учреждений | Мордкович А.Г. | Мнемозина | Москва |
| 10. | Программа по геометрии 8 класса для общеобразовательной школы | Л.С. Атанасян | Просвещение | Москва 2010 |
| 11. | Учебник. Геометрия 7-9 класс | Л.С. Атанасян | Просвещение | Москва 2010 |
| 12. | Контрольные работы, тесты, диктанты по геометрии:8класс | А.В.Фарков | Экзамен | Москва 2008 |
| 13. | Дидактические материалы по геометрии .8класс | Б.Г. Зив, В.М, Мейлер | Просвещение | Москва 2008 |
Календарно-тематический план
| № уро- ка | дата проведения план. /факт | Тема урока и тип урока | Гимназический компонент | Дидакти-ческое и методи-ческое обеспечение | МПС | Элементы обязательного минимума | Домашнее задание |
-
|
|
| Повторение изученного.Линейная функция. Линейные уравнения. Системы линейных уравнений с двумя переменными | Решение задачи повышенного уровня |
|
|
| Задания на карточке |
-
|
|
| Повторение изученного. Одночлены. Многочлены. Разложение многочленов на множители | Решение задачи повышенного уровня |
|
|
| Задания на карточке |
-
|
|
| Основные понятия. Понятие алгебраической дроби (изучение нового) | 1.27,1.32, 1.39 | С-1, Т. 1 | история | Обыкновенные дроби | § 1, 1.5, 1.9,1.11, 1.18, 1.31 |
-
|
|
| Основное свойство алгебраической дроби. Сокращение дробей (комбинированный). | 2.42, 2.44, 2.48
| С-2 Т.1, П.4 |
|
Обыкновенные дроби, формулы сокращенного умножения | § 2, 2.3, 2.4, 2.16, |
-
|
|
| Основное свойство алгебраической дроби. Сокращение дробей. | Сокращение дробей при построении графиков функций
|
|
| § 2 2.25. 2.45 |
-
|
|
| Сложение и вычитание алгебраических дробей с одинаковыми знаменателями (комбинированный). | 3.23, 3.27 | С-3, тест 1 Т.2 | история |
Приведение подобных слагаемых, разложение на множители | § 3,3.7, 3.10, |
-
|
|
| Сложение и вычитание алгебраических дробей с одинаковыми знаменателями. Преобразование рациональных выражений.
| 3.29 |
|
| 3.17, 3.22 |
-
|
|
| Сложение и вычитание алгебраических дробей с разными знаменателями (комбинированный) | 4.49, 4.52, 4.53 | С-4 Т.2 |
| Фор-лы сокр. умножения, разложение на множители | § 4, 4.5, 4.8, 4.10
|
-
|
|
| Сложение и вычитание алгебраических дробей с разными знаменателями. Преобразование рациональных выражений (комбинированный) | 4.49, 4.52, 4.53 | С-4 Т.2 |
| Формулы сокращенного умножения, разложение на множители | § 4, 4.21, 4.20
|
-
|
|
| Сложение и вычитание алгебраических дробей (обобщение и систематизация).
| 4.50, 4.56 | С-5 П.4 |
| Приведение подобных слагаемых. Фор-лы сокр. умножения | § 4 ,4.19, 4.28 |
-
|
|
| Сложение и вычитание алгебраических дробей при решении задач (обобщение и систематизация).
| Преобразование дробей при доказательстве тождеств |
|
|
| 4.31, 4.44, 4.48 |
-
|
|
| Проверочная работа по теме «Сложение и вычитание алгебраических дробей» | Решение задачи повышенного уровня | П.5 |
|
|
|
-
|
|
| Умножение алгебраических дробей. Возведение алгебраических дробей в степень. | 5.375.42 | С-6,7 Т.3 | Исто-рия | Действия с обыкновенными дробями, свойства степени | § 5, 5.3, 5.7, 5.13 |
-
|
|
| Деление алгебраических дробей | 5.43, 5.46 |
|
| Действия с обыкновенными дробями, свойства степени | 5.30, 5.34 |
-
|
|
| Правила преобразования рациональных выражений (изучение нового) | 6.11. 6.13 | П.4 |
| Действия с алгебраическими дробями, формулы сокращенного умножения | § 6 ,6.2, 6.5, 6.8, |
-
|
|
| Преобразование рациональных выражений (обобщение и систематизация) | 6.14,6.19, | С-8, тест 2 |
|
Разложение на множители, формулы сокращенного умножения | § 6 ,6.6 6,9
|
-
|
|
| Преобразование рациональных выражений при решении задач (обобщение и систематизация)
| 6.23, 6.24 |
|
| 6.10, 6.12 6.22 |
-
|
|
| Первые представления о решение рациональных уравнений | 7.32, 7.37, 7.40 рацион. уравнения | С-9 |
| Рациональные числа, решение уравнений | § 7, 7.6, 7.11, 7.14, 7.197.23 |
-
|
|
| Решение простейших рациональных уравнений
| Решение задач повышенной сложности.
|
|
|
|
|
-
|
|
| Степень с отрицательным целым показателем (изучение нового) | 8.25, 8.29, | Т.14 | Физика, химия | Свойства степени, действия со степенями | § 8, 8.2, 8.11, 8.13, 8.17 Зачет №1 |
-
|
|
| Преобразование выражений, содержащих степень с отрицательным целым показателем (закрепление изученного) | 8.27 | С-10, тест 11
| Физика, химия | 8.20, 8.23, 8.28 |
-
|
|
| Обобщающий урок по теме «Алгебраические дроби» Подготовка к контрольной работе № 1 (обобщение и систематизация)
| 8.28, 8.30, 8.31 | П.6 |
| Алгебраич. преобразова-ния | Задание на карточках |
-
|
|
| Контрольная работа №1 по теме «Алгебраические дроби» | Решение задачи повышенного уровня | П.5 |
|
|
|
|
|
-
|
|
| Анализ контрольной работы. Повторение изученного. Треугольники. | Решение задач повышенного уровня сложности |
|
|
| Задания на карточке |
-
|
|
| Повторение изученного. Параллельные прямые | Решение задач повышенного уровня сложности |
|
|
| Задания на карточке |
-
|
|
| Многоугольник. (комбинированный) | Решение задач повышенного уровня сложности | Табл..1, тест 1 |
| Геометр. фигуры | П. 39 – 41;в. 1-5; №364(а, б) 365 (а, б, г), 368 |
-
|
|
| Многоугольник. Решение задач |
|
|
| Геометр. фигуры | 366, 369, 370 |
-
|
|
| Параллелограмм. (комбинированный) |
Решение задач повышенного уровня сложности |
| Алгеб-ра | Сумма углов треугольника, углы при параллельных прямых | § 42, в. 6-8; №371 (а), 372(в), 376(в, г) |
-
|
|
| Признаки параллелограмма. (комбинированный) |
|
| П. 43, в. 9; № 373, 378(устно), 383 |
-
|
|
| Решение задач по теме «Параллелограмм» |
Решение задач повышенного уровня сложности | Т.2, тест2 |
|
| № 375, 380, 384 (устно) |
-
|
|
| Трапеция. (комбинированный) |
|
| алгебра история | Параллельные прямые | П. 44; в. 10-11; № 386, 387, 390; повт. № 384 (устно) |
-
|
|
| Трапеция. Теорема Фалеса. (комбинированный) | Док-во теоремы Фалеса | Т.2, тест3 |
|
| № 391, 392; док-во теоремы Фалеса учить |
-
|
|
| Решение задач на построение. Решение задач по теме «Трапеция» (закрепление) |
Решение задач повышенного уровня сложности |
| Алге-бра | Простейшие задачи на построение | №393 ( б), 394, 398; устно № 396 |
-
|
|
| Прямоугольник. (комбинированный) |
Решение задач повышенного уровня сложности |
| Алгеб-ра | Перпенди-кулярные прямые, св-ва паралле-лограмма | П. 45, в. 12-13; № 399, 401 (а), 404 |
-
|
|
| Ромб. Квадрат. (комбинированный) |
|
| П. 46, в. 14-15; № 405, 409, 411 |
-
|
|
| Решение задач по теме «Прямоуголльник, ромб квадрат» (закрепление) | Решение задач повышенного уровня сложности | Т.3. тест4 |
|
| П. 47, в. 16 – 20, № 415 (б), 413 (а), 410 |
-
|
|
| Осевая и центральная симметрии. Решение задач(комбинирован.) | Творческая работа «Симметрия вокруг нас» |
| алгебра черчение | Св-ва четырехугольников | вопросы к главе 5. |
-
|
|
| Решение задачпо теме «Четырехугольники». Подготовка к контрольной работе № 2 (обобщение и систематизация знаний) | Практиче-ская работа «Четырех-угольники и симметрия» | П.7 |
| Четыреху-гольники и их св-ва | Задание на карточке |
-
|
|
| Контрольная работа№2 по теме «Четырехуголь-ники» |
|
|
|
|
|
|
|
-
|
|
| Анализ к\р. Рациональные числа (комбинированный) | 9.23, 9.25 | С-11 | история | Периодическая дробь | §9, 9.10, 9.16 |
-
|
|
| Решение задач по теме «Рациональные числа» (комбинированный)
| 9.28 |
|
| Периодическая дробь | 9.20, 9.24 |
-
|
|
| Понятие квадратного корня из неотрицательного числа (комбинированный) | 10.38 | С-12 Т.6 |
| Таблица квадратов, | §10, 10.8, 10.14, 10.30 |
-
|
|
| Нахождение квадратного корня из неотрицательного числа при решении уравнений и задач | 10.47 | С-13 | история |
| 10.39 |
-
|
|
| Иррациональные числа. (изучение нового материала) | 11.13, 11.16 |
|
|
| § 11, 11.5, 11.9 |
-
|
|
| Множество действительных чисел (изучение нового) | 12.17, 12.22 | С-14 Т.5 |
|
| § 12, 12.5, 12.6, 12.16 |
-
|
|
| Функция у = √х, ее свойства и график (комбинированный) | 13.20, 13.24, 13.30, | С-15 Т.7 | Физикахимия | Понятие функ-ции, свойства функций | § 13, 13.3, 13.4, |
-
|
|
| Решение задач по теме «Функция у = √х, ее свойства и график» (комбинированный) | 13.31, 13.32 |
|
|
| 13.11,13.17 |
-
|
|
| Свойства квадратных корней (комбинированный) | 14.29, 14.30, 14.36 | С-16, тест 3 Т.8 |
|
| § 14, 14.2, 14.5, 14.7, |
-
|
|
| Свойства квадратных корней. Решение задач (комбинированный) | 14.29, 14.30, 14.36 | С-16, тест 3 Т.8 |
|
| 14.15, 14.18, 14.26 |
-
|
|
| Преобразование выражений, содержащих операцию извлечения квадратного корня. (Урок-практикум) | 15.86, 15.88, | С-17,18 | Физика химия |
| § 15, 15.3, 15.7, 15.12, |
-
|
|
| Преобразование выражений, содержащих операцию извлечения квадратного корня. (Урок-практикум) | 15.90 |
|
|
| 15.18, 15.20, 15.26 |
-
|
|
| Освобождение от иррациональности в знаменателе (обобщение и систематизация) | 15.91, 15.96, | С-19,20 |
| Алгебраичес-кие дроби и действия с дробями | § 15, 15.42, 15.44, 15.49 |
-
|
|
| Модуль действительного числа (изучение нового) | 16.16, 16.29, | С-21,22 | Физика. химия | Понятие модуля и его свойства | § 16, 16.7, 16.13,
|
-
|
|
| Модуль действительного числа, график функции у = |x| Формула √x2= |x|
| 16.34
|
|
|
| 16.19, 16.23, 16.27 |
-
|
|
| Модуль и иррациональность в решении задач
| Модуль и иррац-ть в решении задач | Тест 4 |
|
| 15.74, 15.93, 16.20 |
-
|
|
| Решение задач по теме «Функция у=√х. Свойства квадратного корня». Подготовка к контрольной работе № 3 | Решение задачи повышенного уровня, 16.38, 16.40, 16.44 |
|
|
| Задание на карточке |
-
|
|
| Контрольная работа № 3 по теме «Функция у=√х. Свойства квадратного корня» | Решение задачи повышенного уровня | ДМ |
|
|
|
|
|
-
|
|
| Анализ к\р. Площадь многоугольника. (комбинированный) |
Решение задач повышенного уровня сложности | Т.4, П.5и 6 | алгебра | Прямоуголь-ник и его св-ва | П. 48, 49, в. 1-2; № 448, 449(б), 450 (б), 446 |
-
|
|
| Площадь прямоугольника (комбинированный) |
|
|
| П. 50; в. 3; № 454-456 |
-
|
|
| Площадь параллелограмма. (комбинированный) |
| Т.5, тест 5 | алгебра | Паралле-лограмм и его св-ва | П. 51; в. 4; № 459 (в, г), 460, 464 (а), 462 |
-
|
|
| Площадь треугольника (комбинированный) | Формула Герона |
|
|
| П. 52; в. 5; № 468 (в, г), 469, 473 |
-
|
|
| Площадь треугольника . Теорема об отношении площадей треугольников, имеющих по равному углу. Решение задач.(комбинированный) |
|
|
|
| П. 52, в. 6; № 479 (а), 476 (а), 477 |
-
|
|
| Площадь трапеции. (комбинированный) | Практичес-кая работа «Вычисление площадей» |
| Алгеб-ра
| Трапеция и ее св-ва | П. 53, в. 7; № 480 (б, в), 481, 478, 476 (б) |
-
|
|
| Площадь трапеции. Решение задач на нахождение площадей. (комбинированный) |
| Т.5, тест6 |
| Трапеция и ее св-ва | № 466, 467, 476 (б) |
-
|
|
| Решение задач на нахождение площади четырёхугольников (закрепление) |
|
|
|
| Задания на карточке |
-
|
|
| Теорема Пифагора. (комбинированный) |
Решение задач повышенного уровня сложности | Т.6, П.5 и 6 | алгебра исто-рия | Прямоуголь-ный треугольник и его свойства | П. 54, в. 8; № 483 (в, г), 484 (в, г, д), 486 (в) |
-
|
|
| Теорема, обратная теореме Пифагора (комбинированный) |
|
|
| П. 55; в. 9-10; № 498 (г, д, е), 499 (б), 488 |
-
|
|
| Решение задач по теме «Теорема Пифагора» (закрепление) | Решение задач повышенного уровня сложности | Тест 7, П.5 и 6 | алгебра история
|
| № 489 (а, в), 491 (а), 493 |
-
|
|
| Решение задач по теме «Площадь». Подготовка к контрольной работе № 4. (обобщение и систематизация знаний) |
| П.4 | алгебра | Четыреху-гольники и их свойства | № 495 (б), 494, 490 (а), 524 (устно) |
-
|
|
| Контрольная работа №4 по теме «Площади» |
| П.6 и 3 |
|
|
|
|
|
-
|
|
| Анализ к\р. Функция у = кх2, ее свойства и график ( изучение нового) | 17.53, 17.55 |
|
| Функции, их графики и свойства | § 17, 17.7, 17.12, 17.18, 17.26 |
-
|
|
| Построение графиков квадратичной функции (обобщение и систематизация) | 17.56, 17.62, 17.64, 17.65 | С-23, 24 | Физика. химия | Построение графиков и свойства функций | § 17, 17.28, 17.30, 17.33, 17.43, 17.63 |
-
|
|
| Функция у=к/х, ее св-ва и график. Гипербола. Асимптота |
|
|
|
| § 18, 18.3, 18.6, 18.10, 18.17 |
-
|
|
| Обратная пропорциональность. Построение графиков функций | Постр0ение и чтение графиков кусочных функций | С-25, 26 Т.4 |
| Чтение графиков и их построение | 18.19, 18.36 |
-
|
|
| Обобщающий урок по теме «Квадратичная функция. Функция у=к\х». Подготовка к контрольной работе № 5 | Постр0ение и чтение графиков кусочных функций |
|
|
| Задание на карточках |
-
|
|
| Контрольная работа №5 по теме «Квадратичная функция. Функция у=к\х» (п.17,18)
| Решение задачи повышенного уровня | ДМ |
|
|
|
-
|
|
| Анализ к\р. Построение графика функции y = f (x+l) | 19.36, 19.38 презентация |
| Физика. химия | Графики функций и их свойства | §19, 19.2, 19.6, |
-
|
|
| Построение графика функции y = f (x+l). Решение задач
|
| С-27 |
| Графики функций и их свойства | 19.11, 19.17 |
-
|
|
| Построение графика функции y= f(x)+m | 20.37 презентация |
| Физика. химия | Графики функций и их свойства | § 20, 20.2, 20.7 |
-
|
|
| Построение графика функции y= f(x)+m. Решение задач | 20.40 | С-28 |
| Графики функций и их свойства | 20.11, 20.13 |
-
|
|
| Построение графика функции y= f(x+l)+m | 21.25, 21.26, 21.29 презентация
| С-29 | Физика. химия | Графики функций и их свойства | § 21, 21.3, 21.13, 21.24 |
-
|
|
| Параллельный перенос графика функции. (Практическое занятие) | 21.25, 21.26, 21.29 | С-29 | Физика. химия | Графики функций и их свойства | § 21, 21.7, 21.19 |
-
|
|
| Квадратный трехчлен. Функция у=ах2+bх + с, ее свойства и график | 22.40, 22.42, 22.45, 22.47 | С-30 | Физика. химия | Графики функций и их свойства | § 22, 22.5, 22.6, 22.10, 22.28, |
-
|
|
| Квадратный трехчлен. Функция у=ах2+bх + с, ее свойства и график
| 22.40, 22.42, 22.45, 22.47 | С-30 | Физика. химия | Графики функций и их свойства |
|
-
|
|
| Свойства функции в задачах | 22.52, презентация | С-31 | Физика. химия | Графики функций и их свойства | § 22, 22.19, 22.43, 22.23 |
-
|
|
| Графическое решение квадратных уравнений | 23.13, 23.1 творческие проекты | С-32 |
| Графики функций и их свойства | § 23, 23.2, 23.8, 23.10, 23.20 |
-
|
|
| Решение задач по теме«Квадратичная функция. Функция у=к\х» (п.19-23). Подготовка к контрольной работе № 6
|
|
|
|
| Задания на карточке |
-
|
|
| Контрольная работа № 6 по теме «Квадратичная функция. Функция у=к\х» (п.19-23)
| Решение задачи повышенного уровня
| П.5 |
|
|
|
|
|
-
|
|
| Анализ к\р. Определение подобных треугольников. | Решение задач повышенной сложности |
| алгебра | Четыреху-гольники и их свойства | П. 56-57, в. 1-3; № 535 (устно), 534 (а, б), 536 (а), 538, 542 |
-
|
|
| Отношение площадей подобных треугольников. (комбинированный) | Решение задач повышенной сложности | Т.7, тест8 |
| треугольник | П. 58, в. 4; повт. п. 52; № 543, 544, 546, 549 |
-
|
|
| Первый признак подобия треугольников. (комбинированный) |
| Т.8, П.6 и 5 | алгебра | Подобные треугольни-ки, коэффициент подобия | П. 49, в. 5; № 550, 551 (б), 553, 555 (б) |
-
|
|
| Решение задач на применение первого признака подобия треугольников (закрепление) | Решение задач повышенной сложности |
|
|
| П. 59; № 552 (а, б), 557 (в), 558, 556 |
-
|
|
| Второй и третий признаки подобия треугольников. (комбинированный) |
| Т.8, П.5 и 6 | алгебра | Подобные треуголь -ники, коэффи-циент подобия | П. 60, 61, в. 6, 7; № 559-561 |
-
|
|
| Решение задач на применение второго и третьего признаков подобия треугольников (закрепление) | Решение задач повышенной сложности |
|
|
| № 562, 563, 604, 605 |
-
|
|
| Решение задач на применение признаков подобия треугольников. Подготовка к контрольной работе № 7 (обобщение и систематизация) | Презентация | П. 5и 6 | алгебра |
| Задания на карточке |
|
-
|
|
| Контрольная работа №7 по теме «Подобие треугольников» |
| П.6 и 3 |
|
|
|
|
-
|
|
| Анализ к\р. Средняя линия треугольника. (комбинированный) | Решение задач повышенной сложности | П.5 и 6 | алгебра | Медианы треугольника | П. 62, в. 8, 9; № 556, 570, 571 |
|
-
|
|
| Средняя линия треугольника. Свойство медиан треугольника (комбинированный) |
| П.5 и 6 | алгебра | Медианы треугольника | № 568, 569 |
|
-
|
|
| Пропорциональные отрезки. (комбинированный) | Решение задач повышенной сложности | П. 5и 6 | алгебра | Прямоугольные треугол-ники | П. 63, в. 10, 11; № 572 (а, в, д), 573, 574 (б) |
|
-
|
|
| Пропорциональные отрезки в прямоугольном треугольнике (комбинированный) | Решение задач повышенной сложности | П. 5и 6 | алгебра | Прямоугольные треугол-ники | № 575, 577, 579, 578 (устно) |
|
-
|
|
| Измерительные работы на местности. (комбинированный) | Презентация | П.5 и 6 | алгебра | подобие | П. 64 (с. 150-151), в.13, № 580, 581 |
|
-
|
|
| Задачи на построение методом подобия (комбинированный) |
|
|
|
| № 585 (б, в), 587, 588, 590 |
|
-
|
|
| Синус, косинус и тангенс острого ула прямоугольного треугольника. (комбинированный) | Решение задач повышенной сложности | Т.9, П.5 и 6 | алгебра | Прямоуголь-ные треу-гольники | П. 66; в.15-17; № 591 (в, г), 592 (б, г, е), 593 (в, г) |
|
-
|
|
| Значения синуса,косинуса и тангенса для углов 300. 450 и 600 (комбинированный) | Решение задач повышенной сложности | Т.9, П.5 и 6 | алгебра | Прямоуголь-ные треу-гольники | П. 67, в. 18; № 595, 597, 598 |
|
-
|
|
| Соотношение между сторонами и углами прямоугольного треугольника. Решение задач (закрепление) | Решение задач повышенной сложности | Т.9, тест9 | алгебра |
| Повт. п. 63-67; № 559, 601, 602 |
|
-
|
|
| Решение задач по теме «Подобные треугольники». Подготовка к контрольной работе № 8 (обобщение и систематизация)
|
| П.7 | алгебра |
| № 620, 622, 623, 625, 630 (любые 4 задачи на выбор) |
|
-
|
|
| Контрольная работа №8 по теме «Подобные треугольники» (п. 62-67) | Решение задачи повышенной сложности | П.3 |
|
|
|
|
|
|
|
-
|
|
| Анализ к\р. Основные понятия. Квадратное уравнение. Виды квадратных уравнений. Корень квадратного уравнения (комбинир.) | 24.32, 24.34, | С-33
| Физика. химия | Способы разложения на множители, формулы сокращенного умножения | § 24, 24.3, 24.5,24.15 |
|
-
|
|
| Решение неполных квадратных уравнений (комбинир.) | 24.36, 24.39 | тест 5 Т.9 | Физика. химия | 24.17, 24.24, 24.26 |
|
-
|
|
| Дискриминант. Формулы корней квадратных уравнений (изучение нового) | 25.36, 25.38, | Т.10 |
| Вычислительные навыки, | § 25, 25.3, 25.5, 25.12, 25.26, |
|
-
|
|
| Решение квадратных уравнений с помощью дискриминанта (комбинированный) | 25.44 | С-34 Т.10 | Физика. химия | Преобразование выражений, раскрытие скобок | § 25, 25.32, 25.38 |
|
-
|
|
| Решение квадратных уравнений. Параметр, уравнение с параметром (начальное представление) (комбинированный) | 25.45, 25.48 | С-34 Т.10 | Физика. химия | Преобразование выражений, раскрытие скобок | § 25, 25.17, 25,40 |
|
-
|
|
| Решение уравнений с параметром (начальное представление)
|
| П. 10 |
|
| Задание на карточке |
|
-
|
|
| Рациональные уравнения. Способы решения рациональных уравнений (изучение нового) | 26.18, 26.20, | Т.11 |
| Преобразование алгебраич. выражений | § 26, 26.2, 26.6, 26.9, 26.14, |
|
-
|
|
| Решение рациональных уравнений. (обобщение и систематизация) | 26.21, 26.23, 26.27
| С-35 | Физика химия | Преобразование алгебраических выражений, | § 26, 26.11, 26.15, 26.19 |
|
-
|
|
| Биквадратное уравнение. Метод введения новой переменной. Решение рациональных уравнений (обобщение и систематизация) | Уравнения сводящиеся к квадратным | С-35 | Физика химия | Преобразование алгебраических выражений, | Задание на карточке |
-
|
|
| Решение биквадратных уравнений. Подготовка к контрольной работе № 9 |
|
|
|
| Задание на карточке |
-
|
|
| Контрольная работа № 9 по теме «Квадратные уравнения»(п.24-26) | Решение задачи повышенного уровня | П.5 |
|
|
|
|
|
-
|
|
| Анализ к\р. Взаимное расположение прямой и окружности (комбинированный) | Взаимное располож. двух окруж. | Т.10, П.5 |
| Окружность и понятия с ней связанные | П. 68, в. 1-2; № 631 (в, г), 632, 633 |
-
|
|
| Касательная к окружности. Решение задач (комбинированный) | свойства касательных |
|
| П. 69, в. 3-7; № 634, 636, 639 |
-
|
|
| Градусная мера дуги окружности. (комбинированный) | Решение задач повышенной сложности | Т.11, П.5 | алгебра | Окружность и понятия с ней связан-ные | П. 70, в. 8-10; № 649 (б, г), 650 (б), 651 (б), 652 |
-
|
|
| Теорема о вписанном угле (комбинированный) | Решение задач повышенной сложности | Т.11, П.5 | алгебра | Окружность и понятия с ней связан-ные | П. 71, в. 11-13; № 654 (б, г), 655, 657, 659 |
-
|
|
| Теорема об отрезках пересекающихся хорд (комбинированный) |
| Т.11, тест 10, П.5 | алгебра | Виды углов | П. 71 (с. 173), в. 14; № 666 (б, в), 671 (б), 660, 668 |
-
|
|
| Центральные и вписанные углы. Решение задач. (комбинированный) |
| Т.11, тест 10, П.5 | алгебра | Виды углов | № 661, 663, 673, 672 |
-
|
|
| Свойство биссектрисы угла. (комбинированный) | Четыре замечател. точки треуг-ка. | П.5 и 6 | алгебра | Биссектриса и перпенди-куляр | П. 72 (до серед-го перпенд-ра); в. 15, 16; № 675, 676 (б), 677, 678 (б) |
-
|
|
| Серединный перпендикуляр. Теорема о точке пересечения высот треугольника (комбинированный) | 4 замечат. точки треуг-ка. | П.5 и 6 | алгебра | Биссектриса и перпенди-куляр | П. 72, в. 17-19; № 679 (б), 680(б), 681 |
-
|
|
| Вписанная окружность. (комбинированный) |
| Т.12, П.5 и 6 | алгебра | Четыреху-гольники и их св-ва | П. 74, в. 21, 22; № 689, 692, 693 (б), 694 |
-
|
|
| Свойство описанного четырехугольника. (комбинированный) |
| Т.12, П.5 и 6 | алгебра | Четыреху-гольники и их св-ва | П. 74, в. 23; № 695, 699, 700, 701 |
-
|
|
| Описанная окружность (комбинированный) |
|
| алгебра |
| П. 75, в. 24, 25; № 702 (б), 705 (б), 707, 711 |
-
|
|
| Свойство вписанного четырехугольника. (комбинированный) | Презентация. |
|
|
| В. 1-26; № 709, 710, 731, 735 |
-
|
|
| Решение задач по теме «Окружность». Подготовка к контрольной работе № 11. (обобщение и систематиз. знаний) |
| П.7 | алгебра |
| Задания на карточке |
-
|
|
| Контрольная работа №11 по теме «Окружность» | Решение задачи повышен. сложности | П.3 |
|
| Гл.5 |
|
|
-
|
|
| Анализ к\р. Задачи с параметром | Задачи с параметром |
|
|
| Задание на карточке |
-
|
|
| Рациональные уравнения как математические модели реальных ситуаций (комбинированный) | 27.29 | С-36 | Физика химия | Составление уравнений для решения задач | §27, 27.2, 27.5 |
-
|
|
| Рациональные уравнения как математические модели реальных ситуаций. Решение текстовых задач (комбинированный) | 27.32 | С-36 | Физика химия | Составление уравнений для решения задач | §27, 27.15, 27.20 |
-
|
|
| Рациональные уравнения в решении текстовых задач (закрепления) | 27.42 | С-36 | Физика химия | Составление уравнений для решения задач, квадратные уравнения, рациональные уравнения | § 27, 27.18, 27.24, |
-
|
|
| Рациональные уравнения. Решение текстовых задач (закрепления) | 27.44 | С-36 | Физика химия | § 27, 27.31, 27.35 |
-
|
|
| Формула корней квадратного уравнения с чётным вторым коэффициентом (комбинированный) | 28.20. 28.23, 28.25 | С-37 |
| Квадратные уравнения, и их решение | § 28, 28.2, , 28.6, 28.9, , 28.17, |
-
|
|
| Теорема Виета. (комбинир.) | 29.30, 29.32, | Тест6, С38, 39 | История | Упрощение выражений | § 29, 29.2, 29.7 |
-
|
|
| Теорема Виета. Разложение квадратного трехчлена на линейные множители (комбинированный)
| 29.39, 29.41 | Тест6, С38, 39 | История | Упрощение выражений | § 29, 29.19, 29.23, |
-
|
|
| Иррациональные уравнения. (изучение нового) | 30.18, 30.19 |
|
| Квадрат суммы и разности, квад.уравн. и их решение | § 30, 30.3, 30.7, 30.11, |
-
|
|
| Иррациональные уравнения. Решение простейших иррациональных уравнений | 30.24, 30.23 | С-40 | Физика химия |
| § 30. 30.18, 30.8 |
-
|
|
| Решение иррациональных уравнений. (обобщение и закрепление). Зачет№3 | 30.24, 30.23 | С-40 | Физика химия | Квадрат суммы и разности, квадратные уравнения и их решение | § 30 30.28, 30.24 |
-
|
|
| Решение уравнений и задач по теме «Квадратные уравнения» (п. 27-30). Подготовка к контрольной работе № 10 | Задачи с параметром |
|
| Задания на карточке |
-
|
|
| Контрольная работа № 10 по теме «Квадратные уравнения» (п. 27-30) | Решение задачи повышен-ного уровня | П.5
|
|
| Повт. гл. 5 (учебник геометрии) |
|
|
-
|
|
| Анализ к\р. Повторение изученного по теме «Четырехугольники»
| Опорный конспект | П.5и 7 | алгебра | Четырех-ки и их св-ва | Повт. гл. 6 (учебник геометрии) |
-
|
|
| Повторение изученного по теме «Площадь» (обобщение и систематизация знаний) | Опорный конспект | П.5 и 7 | алгебра | Вычисление площадей фигур | Задания на карточке |
-
|
|
| Повторение изученного по теме «Площадь». Решение задач (обобщение и систематизация знаний) | Опорный конспект | П.5 и 7 | алгебра | Вычисление площадей фигур | Повт. гл. 7 (учебник геометрии) |
-
|
|
| Повторение изученного по теме «Подобные треугольники» (обобщение и систематизация знаний) | Опорный конспект | П. 5 и 7 | алгебра | Подрбие, четыреху-гольники | Задания на карточке |
-
|
|
| Повторение изученного по теме «Подобные треугольники» . Решение задач(обобщение и систематизация знаний) | Опорный конспект | П. 5 и 7 | алгебра | Подрбие, четыреху-гольники | Повт. гл. 8 (учебник геометрии) |
-
|
|
| Повторение изученного по теме «Окружность». Решение задач (обобщение и систематизация знаний) |
| П. 5 и 7 | алгебра |
| Вопросы к зачёту |
-
|
|
| Зачёт по курсу геометрии 8 класса |
|
|
|
|
|
-
|
|
| Зачёт по курсу геометрии 8 класса |
|
|
|
|
|
-
|
|
| Свойства числовых неравенств. Способы решения числовых неравенств. Равносильные неравенства. Равносильные преобразования неравенства (изучение нового) | 31.49, 31.50 | С-41 Т.12 | физика химия | Сравнение чисел, | § 31, 31.14, 31.13, 31.42, 31.46 |
-
|
|
| Решение числовых неравенств. Неравенство Коши (закрепления) | 31.54, 31.58 | Тест 8, Т.12 |
|
Преобразова-ние выражений, свойства неравенств
| § 31, 31.43, 31.27,31.39 |
-
|
|
| Решение числовых неравенств (закрепления) | 31.54 | Тест 8, Т.12 |
| § 31, 31.43, 31.27, 31.39, 31.41 |
-
|
|
| Понятие монотонности функций. Исследование функций на монотонность (линейная функция, квадратичная функция) (комбин.) | 32.12,
|
| физика химия | Графики функций | § 32, 32.3, 32.6, 32.7 |
-
|
|
| Исследование функций на монотонность (обратная пропорциональность, корневая зависимость
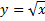 ) ) (комбинир.) |
| С-42 | физика химия | § 32, 32.8, 32.9 |
-
|
|
| Способы решения линейных неравенств (комбинир.) | 33.28, 33.32 | С-43, тест9, 10 |
| Преобразов. выражений, свойства неравенств | § 33, 33.8, 33.16, 33.20 |
-
|
|
| Решение линейных неравенств (комбинир.) | 33.35 | С-43, тест9, 10 |
| § 33, 33.24,33.34 |
-
|
|
| Решение квадратных неравенств. Графический способ (комбинир.) | 34.34, 34.38, | С-44 Табл. |
| Преобразов. выражений, сво-ва нерав., график квадратич. функ-и | § 34, 34.2, 34.10 |
-
|
|
| Решение квадратных неравенств. Метод интервалов (комбинированный) | 34.43 | С-44 Табл. |
| Преобразов. выражений, св-ва нерав-в, график квадрат. функции | § 34, 34.15, 34.27 |
-
|
|
| Решение квадратных неравенств (закрепление). Зачет №4
| 34.44, 34.46
| С-45 |
| Преобразов. выражений, св-ва нерав-в, график квадрат. функции | § 34, 34.11, 34.17, 34.31, 34.36 |
-
|
|
| Приближенные значения действительных чисел, (комбинированный) | 35.10 | С-46 | физика химия | Вычислительные навыки | § 35, 35.7, 35.8, 35.10, 35.13 |
-
|
|
| Стандартный вид положительного числа (изучение нового) | 36.14 | С-47 | физика химия | Св-ва степени, действия со степенями | § 36, 36.7, 36.9, 36.11 |
-
|
|
| Решение неравенств и задач по теме «Неравенства». Подготовка к контрольной работе № 12
| 36.16 |
|
| Задания на карточке |
|
|
| Контрольная работа №12 по теме «Неравенства» | Решение задачи повышенного уровня | П.5 |
|
|
|
-
|
|
| Анализ контрольной работы. Повторение изученного. Алгебраические дроби. | 1.34, 1.40 |
|
| Действия с алгебр.дроб. | Задания на карточке |
-
|
|
| Повторение изученного.Свойства квадратного корня. Квадратные уравнения. |
| П. 5 и 6 | алгебра |
| Задания на карточке |
-
|
|
| Повторение изученного. Рациональные уравнения | 2.6, 2.30 |
| Физика химия | Квадратные, рацион., иррац. урав. | Задания на карточке |
-
|
|
| Повторение изученного. Неравенства | 3.17, 3.30 |
| Физика химия | Линейные, квадратные неравенства | Задания на карточке |
-
|
|
| Повторение изученного. Функции | 4.26, 4.33 |
| Физика химия | Функции, их свойства | Задания на карточке |
-
|
|
| Обобщающий урок за курс математики 8 класса
|
|
|
|
|
|
-
|
|
| Экзаменационная работа |
|
|
|
|
|
-
|
|
|
|
|
|
|
|

 Получите свидетельство
Получите свидетельство Вход
Вход












 Рабочая программа повышенного уровня сложности по математике для 8 класса (0.56 MB)
Рабочая программа повышенного уровня сложности по математике для 8 класса (0.56 MB)
 0
0 655
655 70
70 Нравится
0
Нравится
0


