20
Муниципальное бюджетное общеобразовательное учреждение «Краснослободский многопрофильный лицей»
Краснослободского муниципального района
Республики Мордовия
| Рассмотрена и одобрена на заседании методического объединения учителей математики, физики, информатики Руководитель МО _____________ /Афиногеева В.А./
«_____» ____________ 2014 г.
| Утверждена руководителем образовательного учреждения _______________ /Коршунов В.Д./
«_____»_____________ 2014 г.
|
РАБОЧАЯ ПРОГРАММА
учебного курса «Алгебра» в 8А классе
(базовый уровень)
Составитель:
Бякина Любовь Николаевна
учитель математики высшей
квалификационной категории
2014 - 2015 учебный год
РАБОЧАЯ ПРОГРАММА
ДЛЯ ОСНОВНОГО ОБЩЕГО ОБРАЗОВАНИЯ
(Базовый уровень)
Пояснительная записка
Статус документа
Рабочая программа по математике составлена на основе федерального компонента государственного стандарта основного общего образования.
Данная рабочая программа ориентирована на учащихся 8 классов и реализуется на основе следующих документов:
1. Алгебра. 7 – 9 классы: программы общеобразовательных учреждений/[Составитель Бурмистрова Т.А.] – М.: Просвещение, 2008
2. Стандарт основного общего образования по математике/Математика в школе – 2004г, №4, с.4
Рабочая программа конкретизирует содержание предметных тем образовательного стандарта и дает распределение учебных часов по разделам курса.
Рабочая программа выполняет две основные функции.
Информационно-методическая функция позволяет всем участникам образовательного процесса получить представление о целях, содержании, общей стратегии обучения, воспитания и развития учащихся средствами данного учебного предмета.
Организационно-планирующая функция предусматривает выделение этапов обучения, структурирование учебного материала, определение его количественных и качественных характеристик на каждом из этапов, в том числе для содержательного наполнения промежуточной аттестации учащихся.
Алгебра нацелена на формирование математического аппарата для решения задач по математике, смежных предметов, окружающей реальности. Язык алгебры подчеркивает значение математики как языка для построения математических моделей, процессов и явлений реального мира. Одной из основных задач изучения алгебры является развитие алгоритмического мышления, необходимого, в частности, для освоения курса информатики; овладение навыками дедуктивных рассуждений. Преобразование символических форм вносит свой специфический вклад в развитие воображения, способностей к математическому творчеству. Другой важной задачей изучения алгебры является получение школьниками конкретных знаний о функциях как важнейшей математической модели для описания и исследования разнообразных процессов (равномерных, равноускоренных, экспоненциальных, периодических и др.), для формирования у учащихся представлений о роли математики в развитии цивилизации и культуры.
В ходе освоения содержания курса учащиеся получают возможность:
развить представления о числе и роли вычислений в человеческой практике; сформировать практические навыки выполнения устных, письменных, инструментальных вычислений, развить вычислительную культуру;
овладеть символическим языком алгебры, выработать формально-оперативные алгебраические умения и научиться применять их к решению математических и нематематических задач;
изучить свойства и графики элементарных функций, научиться использовать функционально-графические представления для описания и анализа реальных зависимостей;
развить пространственные представления и изобразительные умения, освоить основные факты и методы планиметрии, познакомиться с простейшими пространственными телами и их свойствами;
получить представления о статистических закономерностях в реальном мире и о различных способах их изучения, об особенностях выводов и прогнозов, носящих вероятностный характер;
развить логическое мышление и речь – умения логически обосновывать суждения, проводить несложные систематизации, приводить примеры и контрпримеры, использовать различные языки математики (словесный, символический, графический) для иллюстрации, интерпретации, аргументации и доказательства;
сформировать представления об изучаемых понятиях и методах как важнейших средствах математического моделирования реальных процессов и явлений.
Цели
Изучение математики на ступени основного общего образования направлено на достижение следующих целей:
овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;
интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе, свойственных математической деятельности: ясности и точности мысли, критичности мышления, интуиции, логического мышления, элементов алгоритмической культуры, пространственных представлений, способности к преодолению трудностей;
формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;
воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, понимание значимости математики для научно-технического прогресса.
Целью изучения курса алгебры 8 является:
систематизация и обобщение сведений о преобразовании выражений и решении уравнений с одним неизвестным;
обеспечение функциональной систематической подготовки учащихся;
формирование базы для выработки умения выполнять тождественные преобразования алгебраических выражений;
формирование умения переводить практические задачи на язык математики.
Основные развивающие и воспитательные цели
Развитие:
Ясности и точности мысли, критичности мышления, интуиции, логического мышления, элементов алгоритмической культуры, пространственных представлений, способности к преодолению трудностей;
Математической речи;
Сенсорной сферы, двигательной моторики;
Внимания, памяти;
Навыков само и взаимопроверки.
Формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов.
Воспитание:
Место предмета в федеральном базисном учебном плане
Согласно федеральному базисному учебному плану для образовательных учреждений Российской Федерации на изучение математики на ступени основного общего образования отводится не менее 875 ч из расчета 5 ч в неделю с V по IX класс. В 8 классе на алгебру приходится 3 ч в неделю, всего 102 ч.
Примерная программа рассчитана на 875 учебных часов. При этом в ней предусмотрены учебные часов для реализации авторских подходов, использования разнообразных форм организации учебного процесса, внедрения современных методов обучения и педагогических технологий.
В настоящей рабочей программе изменено соотношение часов на изучение отдельных тем (подробнее расписано в Содержании тем учебного курса).
Общеучебные умения, навыки и способы деятельности
В ходе преподавания математики в основной школе, работы над формированием у обучающихся перечисленных в программе знаний и умений, следует обращать внимание на то, чтобы они овладевали умениями общеучебного характера, разнообразными способами деятельности, приобретали опыт:
планирования и осуществления алгоритмической деятельности, выполнения заданных и конструирования новых алгоритмов;
решения разнообразных классов задач из различных разделов курса, в том числе задач, требующих поиска пути и способов решения;
исследовательской деятельности, развития идей, проведения экспериментов, обобщения, постановки и формулирования новых задач;
ясного, точного, грамотного изложения своих мыслей в устной и письменной речи, использования различных языков математики (словесного, символического, графического), свободного перехода с одного языка на другой для иллюстрации, интерпретации, аргументации и доказательства;
проведения доказательных рассуждений, аргументации, выдвижения гипотез и их обоснования;
поиска, систематизации, анализа и классификации информации, использования разнообразных информационных источников, включая учебную и справочную литературу, современные информационные технологии.
Результаты обучения
Результаты обучения представлены в Требованиях к уровню подготовки и задают систему итоговых результатов обучения, которых должны достигать все учащиеся, оканчивающие основную школу, и достижение которых является обязательным условием положительной аттестации ученика за курс основной школы. Эти требования структурированы по трем компонентам: «знать/понимать», «уметь», «использовать приобретенные знания и умения в практической деятельности и повседневной жизни». При этом последние два компонента представлены отдельно по каждому из разделов содержания.
ОБЯЗАТЕЛЬНЫЙ МИНИМУМ СОДЕРЖАНИЯ
ОСНОВНЫХ ОБРАЗОВАТЕЛЬНЫХ ПРОГРАММ
АЛГЕБРА
Алгебраические выражения. Буквенные выражения (выражения с переменными). Допустимые значения переменных, входящих в алгебраические выражения. Числовое значение буквенного выражения.
Свойства степеней с целым показателем и их применение в преобразовании выражений. Многочлены. Сложение, вычитание и умножение многочленов. Формулы сокращенного умножения: квадрат суммы и квадрат разности, куб суммы и куб разности. Формула разности квадратов, формула суммы кубов и разности кубов. Разложение многочлена на множители. Вычисления значений арифметических и алгебраических выражений.
Квадратный трехчлен. Выделение полного квадрата в квадратном трехчлене. Разложение квадратного трехчлена на линейные множители. Многочлены с одной переменной. Степень многочлена. Корень многочлена. Алгебраические дроби. Действия с алгебраическими дробями. Преобразования алгебраических выражений.
Уравнения и неравенства. Уравнение с одним неизвестным. Корень уравнения. Линейное уравнение. Квадратное уравнение: формула корней квадратного уравнения, соотношения между коэффициентами и корнями. Решение рациональных уравнений. Примеры решения уравнений высших степеней; методы замены переменной, разложения на множители. Примеры уравнений с несколькими переменными. Системы уравнений. Решение системы. Система двух линейных уравнений с двумя неизвестными. Методы подстановки и алгебраического сложения. Примеры решения нелинейных систем. Примеры решения уравнений в целых числах. Неравенство с одним неизвестным. Решение неравенств. Линейные неравенства с одним неизвестным и их системы. Квадратные неравенства. Примеры решения дробно-линейных неравенств. Примеры доказательств алгебраических неравенств. Составление уравнений, неравенств и их систем по условиям задач. Решение текстовых задач алгебраическим методом.
Координаты
Изображение чисел точками координатной прямой. Геометрический смысл модуля числа. Числовые промежутки: интервал, отрезок, полуинтервал, луч. Формула расстояния между точками координатной прямой.
Декартова система координат на плоскости. Координаты точки на плоскости. Уравнение прямой, уравнение окружности с центром в начале координат. Графическая интерпретация уравнений и неравенств с двумя неизвестными и их систем. Примеры графических зависимостей и функций, отражающих реальные процессы (в том числе периодические – синус; показательный рост).
Числовые функции
Понятие функции. Область определения функции. Способы задания функции. График функции, возрастание и убывание функции, наибольшее и наименьшее значения функции.
Прямая пропорциональность, линейная функция и ее график, геометрический смысл коэффициентов. Обратная пропорциональность и ее график (гипербола).
Квадратичная функция и ее график (парабола). Координаты вершины параболы, ось симметрии. Степенная функция с натуральным показателем и ее график.
Графики функций: корень квадратный, корень кубический, модуль.
Использование графиков функций для решения уравнений и систем.
Использование преобразования графиков (параллельный перенос вдоль осей координат и симметрия относительно осей).
Числовые последовательности и способы их задания
Элементы логики, комбинаторики, статистики и теории вероятностей
Множество. Элемент множества, подмножество. Объединение и пересечение множеств. Диаграммы Эйлера. Понятия об аксиомах и теоремах, следствиях, необходимых и достаточных условиях, контрпримерах, доказательстве от противного. Примеры решения комбинаторных задач: перебор вариантов, правило умножения. Представление данных в виде таблиц, диаграмм, графиков. Средние результаты измерений.
Понятие и примеры случайных событий. Частота события, вероятность. Равновозможные события и подсчет их вероятности. Представление о геометрической вероятности.
ОСНОВНОЕ СОДЕРЖАНИЕ
Алгебра (270ч)
Алгебраические выражения. Буквенные выражения (выражения с переменными). Числовое значение буквенного выражения. Допустимые значения переменных, входящих в алгебраические выражения. Подстановка выражений вместо переменных. Равенство буквенных выражений. Тождество, доказательство тождеств. Преобразование выражений.
Свойства степеней с целым показателем. Многочлены. Сложение, вычитание и умножение многочленов. Формулы сокращенного умножения: квадрат суммы и квадрат разности, куб суммы и куб разности. Формула разности квадратов, формула суммы кубов и разности кубов. Разложение многочлена на множители. Квадратный трехчлен. Выделение полного квадрата в квадратном трехчлене. Теорема Виета. Разложение квадратного трехчлена на линейные множители. Многочлены с одной переменной. Степень многочлена. Корень многочлена.
Алгебраическая дробь. Сокращение дробей. Действия с алгебраическими дробями.
Рациональные выражения и их преобразования. Свойства квадратных корней и их применение в вычислениях.
Уравнения и неравенства. Уравнение с одной переменной. Корень уравнения. Линейное уравнение. Квадратное уравнение; формула корней квадратного уравнения. Решение рациональных уравнений. Примеры решения уравнений высших степеней; методы замены переменной, разложения на множители.
Уравнение с двумя переменными; решение уравнений с двумя переменными. Система уравнений; решение системы. Система двух линейных уравнений с двумя неизвестными; решение системы подстановкой и алгебраическим сложением. Уравнение с несколькими переменными. Примеры решения нелинейных систем. Примеры решения уравнений в целых числах.
Неравенство с одной переменной. Решение неравенства. Линейные неравенства с одной переменной и их системы. Квадратные неравенства. Примеры решения дробно-линейных неравенств.
Числовые неравенства и их свойства. Доказательство числовых и алгебраических неравенств.
Переход от словесной формулировки соотношений между величинами к алгебраической. Решение текстовых задач алгебраическим методом.
Числовые последовательности. Понятие последовательности. Арифметическая и геометрическая прогрессии. Формулы общего члена арифметической и геометрической прогрессий, суммы первых нескольких членов арифметической и геометрической прогрессий. Сложные проценты.
Числовые функции. Понятие функции. Область определения функции. Способы задания функции. График функции, возрастание и убывание функции, наибольшее и наименьшее значения функции, нули функции, промежутки знакопостоянства. Чтение графиков функций.
Функции, описывающие прямую и обратную пропорциональную зависимости, их графики. Линейная функция и ее график, геометрический смысл коэффициентов. Гипербола. Квадратичная функция, ее график, парабола. Координаты вершины параболы, ось симметрии. Степенные функции с натуральным показателем, их графики. Графики функций: корень квадратный, корень кубический, модуль. Использование графиков функций для решения уравнений и систем.
Примеры графических зависимостей, отражающих реальные процессы: колебание, показательный рост; числовые функции, описывающие эти процессы.
Параллельный перенос графиков вдоль осей координат и симметрия относительно осей.
Координаты. Изображение чисел точками координатной прямой. Геометрический смысл модуля числа. Числовые промежутки: интервал, отрезок, полуинтервал, луч. Формула расстояния между точками координатной прямой.
Декартова система координат на плоскости; координаты точки. Координаты середины отрезка. Формула расстояния между двумя точками плоскости. Уравнение прямой, угловой коэффициент прямой, условие параллельности прямых. Уравнение окружности с центром в начале координат и в любой заданной точке.
Графическая интерпретация уравнений с двумя переменными и их систем, неравенств с двумя переменными и их систем.
Элементы логики, комбинаторики, статистики и теории вероятностей(45ч)
Доказательство. Определения, доказательства, аксиомы и теоремы, следствия. Необходимые и достаточные условия. Контрпример. Доказательство от противного. Прямая и обратная теоремы.
Понятие об аксиоматике и аксиоматическом построении геометрии. Пятый постулат Евклида и его история.
Множества и комбинаторика. Множество. Элемент множества, подмножество. Объединение и пересечение множеств. Диаграммы Эйлера.
Примеры решения комбинаторных задач: перебор вариантов, правило умножения.
Статистические данные. Представление данных в виде таблиц, диаграмм, графиков. Средние результаты измерений. Понятие о статистическом выводе на основе выборки. Понятие и примеры случайных событий.
Вероятность. Частота события, вероятность. Равновозможные события и подсчет их вероятности. Представление о геометрической вероятности.
Тематическое планирование
по алгебре в 8 классе
| № n/n | Наименование разделов и тем | Максимальная нагрузка (ч) | Из них |
| Теоретическое обучение (ч) | Решение задач (ч) | Контрольные работы (ч) | Самостоятельные работы, практические работы, тесты |
|
| Повторение курса алгебры 8 класса | 2ч |
| 1 | 1 |
|
| I. | Неравенства | 19ч | 8 | 10 | 1 | 5 |
| II. | Приближённые вычисления | 9ч | 3 | 6 | − | 1 |
| III. | Квадратные корни | 14ч | 4 | 9 | 1 | 5 |
| IV. | Квадратные уравнения | 24ч | 8 | 15 | 1 | 5 |
| V. | Квадратичная функция | 16ч | 5 | 10 | 1 | 3 |
| VI. | Квадратные неравенства | 13ч | 4 | 8 | 1 | 4 |
|
| Повторение. Решение задач | 5ч | 2 | 2 | 1 | − |
|
| Итого | 102 | 34 | 61 | 7 | 23 |
СОДЕРЖАНИЕ ТЕМ УЧЕБНОГО КУРСА
АЛГЕБРА, 8 класс
(3ч. в неделю, всего 102ч.)
1. Повторение курса алгебры 7 класса (2ч)
2. Неравенства (19ч)
Положительные и отрицательные числа. Числовые неравенства, их свойства. Сложение и умножение неравенств. Строгие и нестрогие неравенства. Неравенства с одним неизвестным. Системы неравенств с одним неизвестным. Числовые промежутки.
Основная цель – Обобщить сведения о свойствах положительных и отрицательных чисел и ознакомит с применением этих свойств при решении уравнений; формировать умение применять свойства числовых неравенств при решении простейших задач на сравнение чисел и доказательства неравенств; формировать у учащихся умение складывать и умножать неравенства; сформировать у учащихся умение решать неравенства первой степени с одним неизвестным и их системы.
Знать определение рационального числа, определение числового неравенства и его основные свойства, формулировки теорем сложения и умножения неравенств, понятие линейного неравенства с одним неизвестным и его решения, что называется решением системы неравенств.
Уметь применять свойства чисел при выполнении упражнений (в частности, решении уравнений), применять определение числового неравенства при решении упражнений, применять свойства числовых неравенств при решении задач, применять теоремы сложения и умножения неравенств при решении упражнений, решать неравенства с одним неизвестным и их системы, используя их геометрическую иллюстрацию.
Осознавать ценность полученных знаний и умений при решении различных задач, важность овладения речевой культурой и культурой диалога.
3. Приближенные вычисления (9ч)
Приближенные значения величин. Погрешность приближения. Оценка погрешности. Округление чисел. Относительная погрешность. Простейшие вычисления на калькуляторе. Стандартный вид числа. Вычисление на микрокалькуляторе степени числа и числа, обратного данному. Последовательное выполнение операций на микрокалькуляторе. Вычисления на микрокалькуляторе с использованием ячейки памяти.
Основная цель – познакомить учащихся с понятием погрешности приближения, как показателем точности и качества приближения, выработать умение производить вычисления с помощью калькулятора.
Знать определение абсолютной погрешности, правила округления чисел, понятие относительной погрешности, как оценки качества приближения, назначение основных клавиш для выполнения арифметических операций, алгоритм выполнения нескольких операций, алгоритм выполнения операция с использованием ячеек памяти.
Уметь находить абсолютную погрешность, приближенные значения с недостатком и с избытком при заданной точности приближения, округлять числа, находить относительную погрешность, включать калькулятор на компьютере, вводить числа и выполнять арифметические действия на калькуляторе, применять ячейки памяти при выполнении арифметических действий на МК, вести себя в компьютерном классе в соответствии с правилами техники безопасности и гигиеническими нормами.
Осознать самооценку саморазвития уровня интеллектуальных способностей, ценность полученных знаний и умений при решении различных задач, а также уметь применять свои знания на уроках физики, значение умений пользоваться калькулятором для рядового члена общества.
4. Квадратные корни (14ч)
Понятие арифметического квадратного корня. Действительные числа. Квадратный корень из степени, произведения и дроби.
Основная цель – систематизировать сведения о рациональных числах, ввести понятия иррационального и действительного чисел, научить выполнять простейшие преобразования выражений, содержащих квадратные корни.
Знать определение арифметического квадратного корня из числа, определение рационального и иррационального чисел, определение понятия тождества, теорему о корне из произведения и из дроби.
Уметь применять определение арифметического квадратного корня при решении упражнений, обращать бесконечную периодическую десятичную дробь в обыкновенную, с помощью МК выполнять практические действия над иррациональными числами, заменяя их десятичными приближениями, выносить множитель из-под знака корня и вносить множитель под знак корня, выполнять деление квадратных корней, избавляться от иррациональности в знаменателе дроби.
Осознавать ценность информации в человеческой деятельности; ценности применения методов тождественных преобразований при изучении смежных дисциплин.
5. Квадратные уравнения (24ч)
Квадратное уравнение и его корни. Неполные квадратные уравнения. Метод выделения полного квадрата. Решение квадратных уравнений. Разложение квадратного трехчлена на множители. Уравнения, сводящиеся к квадратным. Решение задач с помощью уравнений. Решение простейших систем, содержащих уравнение второй степени. Уравнение окружности.
Основная цель – выработать умения решать квадратные уравнения, умения решать уравнения, сводящиеся к квадратным, умения решать задачи с помощью квадратных уравнений, рассмотреть методы решения систем уравнений второй степени, причем основное внимание уделяется решению систем, в которых одно из уравнений второй степени, а другое первой, способом подстановки.
Знать общий вид квадратного уравнения и называть его коэффициенты, методы решений неполных квадратных уравнений, метод выделения полного квадрата, формулу корней приведенного квадратного уравнения (Формула Виета).
Уметь решать квадратные уравнения общего вида, неполные квадратные уравнения, приведенные квадратные уравнения с помощью формулы Виета, задачи с помощью составления квадратных уравнений.
Осознавать самооценку саморазвития уровня интеллектуальных способностей; важность овладения речевой культурой и культурой диалога.
6. Квадратичная функция (16ч)
Определение квадратичной функции. Функции y = x2, y = ax2, y = ax2 + bx + c. Построение графика квадратичной функции.
Основная цель – научить строить график квадратичной функции, формировать умение определять по графику промежутки возрастания и убывания функции, промежутки знакопостоянства, нули функции, повторить решение систем двух уравнений, одно из которых первой, а другое второй степени.
Знать понятие квадратичной функции и нулей функции, как выглядит и как называется график функции y = x2, формулы нахождения координат вершин параболы, алгоритм построения параболы.
Уметь по графику функции y = x2 перечислять ее свойства, по формуле, задающей функцию вида y = аx2, определять направление ветвей параболы, строить по точкам, с использованием свойств симметрии параболы y = аx2 относительно оси Оу, графики функций вида y=аx2 при конкретных значениях а, находить координаты вершины параболы, строить ось симметрии, определять направление ветвей параболы, строить параболу методом сдвигов, строить параболу по заданному алгоритму.
Осознавать ценность полученных знаний и умений при решении различных задач, а также уметь применять свои знания на уроках физики, геометрии; значимость и ответственность за качество приобретенных знаний и умений; важность овладение приемами самоконтроля и самооценки; необходимость способности к самооценке в диалоге, умения принимать критику.
7. Квадратные неравенства (13ч)
Квадратное неравенство и его решение. Решение квадратного неравенства с помощью графика квадратичной функции. Метод интервалов.
Основная цель – выработать умение решать квадратные неравенства с помощью графика квадратичной функции, привести аналитический способ решения квадратных неравенств, повторить свойства квадратичной функции (нахождение координат вершины и направление ветвей параболы), при наличии времени познакомить учащихся с методом интервалов.
Знать понятие квадратичного неравенства, аналитический способ решения квадратичного неравенства, алгоритм решения квадратичного неравенства методом интервалов.
Уметь решать квадратичные неравенства аналитическим способом, с помощью графика квадратичной функции, применять метод интервалов при решении квадратичного неравенства.
Осознавать, что введение новых выражений обусловлено потребностями практики, а также внутренними потребностями математики; роль математики в повседневной жизни человека; ценности применения методов тождественных преобразований при изучении смежных дисциплин.
8. Повторение. Решение задач (5ч)
Закрепление знаний, умений и навыков, полученных по данным темам на уроках алгебры 8 класса.
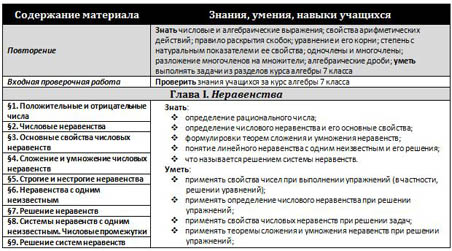
| Содержание материала | Знания, умения, навыки учащихся |
| Повторение | Знать числовые и алгебраические выражения; свойства арифметических действий; правило раскрытия скобок; уравнение и его корни; степень с натуральным показателем и ее свойства; одночлены и многочлены; разложение многочленов на множители; алгебраические дроби; уметь выполнять задачи из разделов курса алгебры 7 класса |
| Входная проверочная работа | Проверить знания учащихся за курс алгебры 7 класса |
| Глава I. Неравенства |
| §1. Положительные и отрицательные числа | Знать: определение рационального числа; определение числового неравенства и его основные свойства; формулировки теорем сложения и умножения неравенств; понятие линейного неравенства с одним неизвестным и его решения; что называется решением системы неравенств. Уметь: применять свойства чисел при выполнении упражнений (в частности, решении уравнений); применять определение числового неравенства при решении упражнений; применять свойства числовых неравенств при решении задач; применять теоремы сложения и умножения неравенств при решении упражнений; решать неравенства с одним неизвестным и их системы, используя их геометрическую иллюстрацию |
| §2. Числовые неравенства |
| §3. Основные свойства числовых неравенств |
| §4. Сложение и умножение числовых неравенств |
| §5. Строгие и нестрогие неравенства |
| §6. Неравенства с одним неизвестным |
| §7. Решение неравенств |
| §8. Системы неравенств с одним неизвестным. Числовые промежутки |
| §9. Решение систем неравенств |
| §10. Модуль числа. Уравнения и неравенства, содержащие модуль |
| Решение задач. Подготовка к контрольной работе | Закрепить в процессе решения задач, полученные знания, умения и навыки, подготовить учащихся к предстоящей контрольной работе |
| Контрольная работа №1 «Неравенства» | Уметь применять все полученные знания при решении упражнений |
| Глава II. Приближённые вычисления |
| §11. Приближённые значения величин. Погрешность приближения | Знать: определение абсолютной погрешности; правила округления чисел; понятие относительной погрешности как оценки качества приближения; назначение основных клавиш для выполнения арифметических операций; алгоритм выполнения нескольких операций; алгоритм выполнения операция с использованием ячеек памяти. Уметь: находить абсолютную погрешность; находить приближенные значения с недостатком и с избытком при заданной точности приближения; округлять числа; находить относительную погрешность; включать калькулятор на компьютере, вводить числа и выполнять арифметические действия на калькуляторе; применять ячейки памяти при выполнении арифметических действий на МК; вести себя в компьютерном классе в соответствии с правилами техники безопасности и гигиеническими нормами |
| §12. Оценка погрешности |
| §13. Округление чисел |
| §14. Относительная погрешность |
| §15. Простейшие вычисления на микрокалькуляторе |
| §16. Стандартный вид числа |
| §17. Вычисления на микрокалькуляторе степени числа и числа, обратного данному |
| §18. Последовательное выполнение операций на микрокалькуляторе |
| §19. Вычисления на микрокалькуляторе с использованием ячейки памяти |
| Глава III. Квадратные корни |
| §20. Арифметический квадратный корень | Знать: определение арифметического квадратного корня из числа; определение рационального и иррационального чисел; определение понятия тождества; теорему о корне из произведения, из дроби; Уметь: применять определение арифметического квадратного корня при решении упражнений; обращать бесконечную периодическую десятичную дробь в обыкновенную; с помощью МК выполнять практические действия над иррациональными числами, заменяя их десятичными приближениями; выносить множитель из-под знака корня и вносить множитель под знак корня; выполнять деление квадратных корней; избавляться от иррациональности в знаменателе дроби. |
| §21. Действительные числа |
| §22. Квадратный корень из степени |
| §23. Квадратный корень из произведения |
| §24. Квадратный корень из дроби |
| Решение задач. Подготовка к контрольной работе | Привести в систему знания по данной теме, уметь применять весь изученный материал при решении задач, подготовить учащихся к предстоящей контрольной работе |
| Контрольная работа №2 «Квадратные корни» | Уметь применять все полученные знания при решении упражнений |
| Глава IV. Квадратные уравнения |
| §25. Квадратное уравнение и его корни | Знать: общий вид квадратного уравнения и называть его коэффициенты; методы решений неполных квадратных уравнений; метод выделения полного квадрата; формулу корней приведенного квадратного уравнения. (Формула Виета). Уметь: решать квадратные уравнения общего вида; решать неполные квадратные уравнения; решать приведенные квадратные уравнения с помощью формулы Виета; решать задачи с помощью составления квадратных уравнений
|
| §26. Неполные квадратные уравнения |
| §27. Метод выделения полного квадрата |
| §28. Решение квадратных уравнений |
| §29. Приведённое квадратное уравнение. Теорема Виета |
| §30. Уравнения, сводящиеся к квадратным |
| Проверочная работа |
| §31. Решение задач с помощью квадратных уравнений |
| §32. Решение простейших систем, содержащих уравнения второй степени |
| §33.* Комплексные числа |
| §34.* Квадратные уравнения с комплексными числами |
| Решение задач. Подготовка к контрольной работе | Закрепить в процессе решения задач, полученные знания, умения и навыки, подготовить учащихся к предстоящей контрольной работе |
| Контрольная работа №3 «Квадратные уравнения» | Уметь применять все полученные знания при решении упражнений |
| Глава V. Квадратичная функция |
| §35. Определение квадратичной функции | Знать: понятие квадратичной функции и нулей функции; как выглядит и как называется график функции y = x2; формулы нахождения координат вершин параболы; алгоритм построения параболы. Уметь: по графику функции y = x2 перечислять ее свойства; по формуле, задающей функцию вида y = аx2, определять направление ветвей параболы, строить по точкам с использованием свойств симметрии параболы y = аx2 относительно оси Оу графики функций вида y=аx2 при конкретных значениях а; находить координаты вершины параболы, строить ось симметрии, определять направление ветвей параболы; строить параболу методом сдвигов; строить параболы по заданному алгоритму |
| §36. Функция y = x2 |
| §37. Функция y = ax2 |
| §38. Функция y = ax2 + bx + c |
| §39. Построение графика квадратичной функции |
| Решение задач. Подготовка к контрольной работе | Закрепить в процессе решения задач, полученные знания, умения и навыки, подготовить учащихся к предстоящей контрольной работе |
| Контрольная работа №4 «Квадратичная функция» | Уметь применять все полученные знания при решении упражнений |
| Глава VI. Квадратные неравенства |
| §40. Квадратное неравенство и его решение | Знать: понятие квадратичного неравенства; аналитический способ решения квадратичного неравенства; алгоритм решения квадратичного неравенства методом интервалов. Уметь: решать квадратичные неравенства аналитическим способом; решать квадратичные неравенства с помощью графика квадратичной функции; применять метод интервалов при решении квадратичного неравенства |
| §41. Решение квадратного неравенства с помощью графика квадратичной функции |
| §42. Метод интервалов |
| §43. Исследование квадратного трехчлена |
| Решение задач. Подготовка к контрольной работе | Закрепить в процессе решения задач, полученные знания, умения и навыки, подготовить учащихся к предстоящей контрольной работе |
| Контрольная работа №5 «Квадратные неравенства» | Уметь применять все полученные знания при решении упражнений |
| Повторение. Решение задач | Закрепление знаний, умений и навыков, полученных на уроках по всем темам курса алгебры 7класса. Систематизировать сведения об основных свойствах, повторить способы решения, наиболее важные законы; не менее половины каждого урока отводить на решение задач |
Основной формой организации учебного процесса является классно-урочная система. В качестве дополнительных форм организации образовательного процесса по данной программе используется система консультационной поддержки, индивидуальных занятий, работа учащихся с использованием современных информационных технологий. Система уроков условна, но все же выделяются следующие виды:
Урок–лекция. Предполагаются совместные усилия учителя и учеников для решения общей проблемной познавательной задачи. На таком уроке используется демонстрационный материал на компьютере, разработанный учителем или учениками, мультимедийные продукты.
Урок–практикум. На уроке учащиеся работают над различными заданиями в зависимости от своей подготовленности. Виды работ могут быть самыми разными: письменные исследования, решение различных задач, изучение свойств различных функций, практическое применение различных методов решения задач. Компьютер на таких уроках используется как электронный калькулятор, тренажер устного счета, виртуальная лаборатория, источник справочной информации.
Урок–исследование. На уроке учащиеся решают проблемную задачу исследовательского характера аналитическим методом и с помощью компьютера с использованием различных лабораторий.
Комбинированный урок предполагает выполнение работ и заданий разного вида.
Урок–игра. На основе игровой деятельности учащиеся познают новое, закрепляют изученное, отрабатывают различные учебные навыки.
Урок решения задач. Вырабатываются у учащихся умения и навыки решения задач на уровне обязательной и возможной подготовке. Любой учащийся может использовать компьютерную информационную базу по методам решения различных задач, по свойствам элементарных функций и т.д.
Урок–тест. Тестирование проводится с целью диагностики пробелов знаний, контроля уровня обученности учащихся, тренировки технике тестирования. Тесты предлагаются как в печатном, так и в компьютерном варианте. Причем в компьютерном варианте, всегда с ограничением времени.
Урок–зачет. Устный опрос учащихся по заранее составленным вопросам, а также решение задач разного уровня по изученной теме.
Урок – самостоятельная работа. Предлагаются разные виды самостоятельных работ.
Урок – контрольная работа. Проводится на двух уровнях:
А – уровень обязательной подготовки, В – уровень возможной подготовки.
Компьютерное обеспечение уроков
В разделе рабочей программы «Компьютерное обеспечение» спланировано применение имеющихся компьютерных продуктов: демонстрационный материал, задания для устного опроса учащихся, тренировочные упражнения, а также различные электронные учебники.
Демонстрационный материал (слайды).
Создается с целью обеспечения наглядности при изучении нового материала, использования при ответах учащихся. Применение анимации при создании такого компьютерного продукта позволяет рассматривать вопросы математической теории в движении, обеспечивает другой подход к изучению нового материала, проявляется повышенное внимание и интерес у учащихся.
При решении любых задач использование графической интерпретации условия задачи, ее решения позволяет учащимся понять математическую идею решения, более глубоко осмыслить теоретический материал по данной теме.
Задания для устного счета.
Эти задания дают возможность в устном варианте отрабатывать различные вопросы теории и практики, применяя принципы наглядности, доступности. Их можно использовать на любом уроке в режиме учитель – ученик, взаимопроверки, а также в виде тренировочных занятий.
Тренировочные упражнения.
Включают в себя задания с вопросами и наглядными ответами, составленными с помощью анимации. Они позволяют ученику самостоятельно отрабатывать различные вопросы математической теории и практики.
Электронные учебники.
Они используются в качестве виртуальных лабораторий при проведении практических занятий, уроков введения новых знаний. В них заключен большой теоретический материал, много тренажеров, практических и исследовательских заданий, справочного материала. На любом из уроков возможно использование компьютерных устных упражнений, применение тренажера устного счета, что активизирует мыслительную деятельность учащихся, развивает вычислительные навыки, так как позволяет осуществить иной подход к изучаемой теме.
Использование компьютерных технологий в преподавании математики позволяет непрерывно менять формы работы на уроке, постоянно чередовать устные и письменные упражнения, осуществлять разные подходы к решению математических задач, а это постоянно создает и поддерживает интеллектуальное напряжение учащихся, формирует у них устойчивый интерес к изучению данного предмета.
В ходе реализации данной программы предусмотрены следующие виды и формы контроля: самостоятельные работы, тестирование, математические диктанты, контрольные работы.
УСЛОВНЫЕ ОБОЗНАЧЕНИЯ
| Тип урока | Форма контроля |
| УОНМ – урок ознакомления с новым материалом | МД – математический диктант |
| УЗИМ – урок закрепления изученного материала | СР – самостоятельная работа |
| УПЗУ – урок применения знаний и умений | СРСУ – самостоятельная работа с учебником |
| УОСЗ – урок обобщения и систематизации знаний | ПР – практическая работа |
| УКЗУ – урок контроля знаний и умений | ИЗ – индивидуальные задания |
| КУ – комбинированный урок | КР – контрольная работа |
| УЛ – урок лекция | ИРД – индивидуальная работа у доски |
|
| ИРК – индивидуальная работа по карточкам |
|
| ДСР – дифференцированная самостоятельная работа |
|
| ДПР – дифференцированная проверочная работа |
|
| Т – тестовая работа |
|
| СРЗ – самостоятельное решение задач |
Календарно-тематическое планирование
Уроков алгебры
(предмет)
Классы:_____8 класс___________________________
Учитель:____Бякина Любовь Николаевна__________
Количество часов за год:
Всего _____102 часа_________
В неделю ____3 часа_________
Плановых контрольных работ: ____ 7_____ , самостоятельных, практических работ и тестов: _________23_________
Планирование составлено на основе ___ Программы общеобразовательных учреждений: алгебра 7–9кл. /Сост.___ Бурмистрова Т.А.– М: Просвещение, 2008/, рекомендована Министерством образования Российской____________ Федерации, в соответствии с федеральным компонентом государственного образовательного_______________ стандарта по предмету математика, примерной программой среднего (полного) общего образования,_________ Федеральным базисным планом_________________________________________________________________________
Учебник_ Алгебра. 8 класс: учебник для общеобразовательных организаций/[Ш.А. Алимов, Ю.М. Колягин, Ю.В.____ Сидоров, М.В. Ткачева, Н.Е. Федорова, М.И. Шабунин] – М.: Просвещение, 2010
Примерное планирование учебного материала по алгебре в 8 классе
| № урока | № параграфа | Содержание учебного материала | Количество часов | Тип урока | Виды самостоятельной работы | Контрольные работы | Дата проведения |
| планируемая | фактическая |
| 1, 2 |
| Повторение курса алгебры 7 класса | 3ч | КУ | СРСУ, ИРД | 1 | 02,03.09 |
|
| 3 |
| Входная проверочная работа |
| УКЗУ | КР | 1 | 09.09 |
|
| Глава I. | Неравенства | 19ч |
|
| 1 |
|
|
| 4, 5 | §1 | Положительные и отрицательные числа | 2 | УОНМ, УЗИМ, УЛ | МД, СРСУ |
| 06, 10.09 |
|
| 6 | §2 | Числовые неравенства | 1 | УОНМ, УЗИМ, КУ | СР, ИРД |
| 13.09 |
|
| 7, 8 | §3 | Основные свойства числовых неравенств | 2 | КУ | МД, ИРД |
| 16, 17.09 |
|
| 9 | §4 | Сложение и умножение числовых неравенств | 1 | КУ | СР, ИРК, ИРД |
| 20.09 |
|
| 10 | §5 | Строгие и нестрогие неравенства | 1 | КУ | ИРК, ИРД |
| 23.09 |
|
| 11 | §6 | Неравенства с одним неизвестным | 1 | КУ | ИРД |
| 24.09 |
|
| 12–14 | §7 | Решение неравенств | 3 | УОНМ, УЗИМ, КУ | СР, ИРД |
| 27, 30.09, 04.10 |
|
| 15 | §8 | Системы неравенств с одним неизвестным. Числовые промежутки | 1 | КУ | ИРД |
| 07.10 |
|
| 16–18 | §9 | Решение систем неравенств | 3 | УОНМ, УЗИМ, КУ | СРСУ, ИЗ, ИРК |
| 08, 11, 14.10 |
|
| 19, 20 | §10 | Модуль числа. Уравнения и неравенства, содержащие модуль | 2 | УОНМ, УЗИМ, КУ | СР, ПР, ИРД |
| 15, 18.10 |
|
| 21 |
| Решение задач. Подготовка к контрольной работе | 1 | УЗИМ, УОСЗ | СРЗ, ИЗ |
| 21.10 |
|
| 22 |
| Контрольная работа №1 «Неравенства» | 1 | УКЗУ | КР | 1 | 22.10 |
|
| Глава II. | Приближённые вычисления | 9ч |
|
| − |
|
|
| 23 | §11 | Приближённые значения величин. Погрешность приближения | 1 | КУ | СРСУ |
| 25.10 |
|
| 24 | §12 | Оценка погрешности | 1 | КУ | СР |
| 28.10 |
|
| 25 | §13 | Округление чисел | 1 | КУ | ИРД |
| 29.10 |
|
| 26 | §14 | Относительная погрешность | 1 | КУ | ИРК |
| 01.11 |
|
| 27 | §15 | Простейшие вычисления на микрокалькуляторе | 1 | КУ | ПР, ДСР |
| 11.11 |
|
| 28 | §16 | Стандартный вид числа | 1 | КУ | СРЗ, ИЗ |
| 12.11 |
|
| 29 | §17 | Вычисления на микрокалькуляторе степени числа и числа, обратного данному (Проверочная работа) | 1 | КУ | ПР, ДСР |
| 15.11 |
|
| 30 | §18 | Последовательное выполнение операций на микрокалькуляторе | 1 | КУ | СРСУ |
| 18.11 |
|
| 31 | §19 | Вычисления на микрокалькуляторе с использованием ячейки памяти | 1 | КУ | СР |
| 19.11 |
|
| Глава III. | Квадратные корни | 14ч |
|
| 1 |
|
|
| 32, 33 | §20 | Арифметический квадратный корень | 2 | УОНМ, УЗИМ | СРСУ |
| 22, 25.11 |
|
| 34, 35 | §21 | Действительные числа | 2 | УОНМ, УЗИМ | СР |
| 26, 29.11 |
|
| 36–38 | §22 | Квадратный корень из степени | 3 | УОНМ, УЗИМ | ИРД |
| 02, 03, 06.12 |
|
| 39, 40 | §23 | Квадратный корень из произведения | 2 | УОНМ, УЗИМ | ИРК |
| 09, 10.12 |
|
| 41, 42 | §24 | Квадратный корень из дроби | 2 | УОСЗ, УПЗУ | ДСР |
| 13, 16.12 |
|
| 43, 44 |
| Решение задач. Подготовка к контрольной работе | 2 | УПЗУ, УЗИМ, УОСЗ | СРЗ, ИЗ |
| 17, 20.12 |
|
| 45 |
| Контрольная работа №2 «Квадратные корни» | 1 | УКЗУ | КР | 1 | 23.12 |
|
| Глава IV. | Квадратные уравнения | 24ч |
|
| 1 |
|
|
| 46 | §25 | Квадратное уравнение и его корни | 1 | УОНМ, УЗИМ | СРСУ |
| 24.12 |
|
| 47 | §26 | Неполные квадратные уравнения | 1 | УОНМ, УЗИМ | СР |
| 27.12 |
|
| 48 | §27 | Метод выделения полного квадрата | 1 | УОНМ, УЗИМ | ИРД |
| 13.01 |
|
| 49–52 | §28 | Решение квадратных уравнений | 4 | УОНМ, УЗИМ | ИРК, ДСР |
| 14, 17, 20, 21.01 |
|
| 53, 54 | §29 | Приведённое квадратное уравнение. Теорема Виета | 2 | УОСЗ, УПЗУ | ДСР |
| 24, 27.01 |
|
| 55–57 | §30 | Уравнения, сводящиеся к квадратным | 3 | УПЗУ, УЗИМ, УОСЗ | СРЗ, ИЗ |
| 28, 31.01, 03.02 |
|
| 58 |
| Проверочная работа | 1 | УКЗУ | ДСР |
| 04.02 |
|
| 59–62 | §31 | Решение задач с помощью квадратных уравнений | 4 | УОНМ, УЗИМ | ИЗ, ДСР, ИРД |
| 07, 10, 11, 14.02 |
|
| 63–65 | §32 | Решение простейших систем, содержащих уравнения второй степени | 3 | УОНМ, УЗИМ | СР, ИРД |
| 17, 18, 21.02 |
|
| 66 | §33* | Комплексные числа | 1 | УОНМ, УЗИМ | СР |
| 24.02 |
|
| 67 | §34* | Квадратные уравнения с комплексными числами | 1 | УОНМ, УЗИМ | СРСУ |
| 25.02 |
|
| 68 |
| Решение задач. Подготовка к контрольной работе | 1 | УПЗУ, УЗИМ, УОСЗ | СРЗ, ИЗ |
| 28.02 |
|
| 69 |
| Контрольная работа №3 «Квадратные уравнения» | 1 | УКЗУ | КР | 1 | 03.03 |
|
| Глава V. | Квадратичная функция | 16ч |
|
| 1 |
|
|
| 70 | §35 | Определение квадратичной функции | 1 | УОНМ, УЗИМ | СРСУ |
| 04.03 |
|
| 71 | §36 | Функция y = x2 | 1 | УОНМ, УЗИМ | СР |
| 07.03 |
|
| 72–74 | §37 | Функция y = ax2 | 3 | УОНМ, УЗИМ | ИРД, СР |
| 10, 11, 14.03 |
|
| 75–77 | §38 | Функция y = ax2 + bx + c | 3 | УОНМ, УЗИМ | ИРК, ИРД, ДСР |
| 17, 18, 21.03 |
|
| 78–82 | §39 | Построение графика квадратичной функции | 5 | УЛ, УОСЗ, УПЗУ | ДСР, ПР |
| 30, 31.03, 04, 07, 08.04 |
|
| 83, 84 |
| Решение задач. Подготовка к контрольной работе | 2 | УПЗУ, УЗИМ, УОСЗ | СРЗ, ИЗ |
| 11, 14.04 |
|
| 85 |
| Контрольная работа №4 «Квадратичная функция» | 1 | УКЗУ | КР | 1 | 15.04 |
|
| Глава VI. | Квадратные неравенства | 13ч |
|
| 1 |
|
|
| 86, 87 | §40 | Квадратное неравенство и его решение | 2 | УОНМ, УЗИМ | СРСУ |
| 18, 21.04 |
|
| 88–91 | §41 | Решение квадратного неравенства с помощью графика квадратичной функции | 4 | УОНМ, УЗИМ | ДСР, ИРК, СР |
| 22, 25, 28, 29.04 |
|
| 92–95 | §42 | Метод интервалов | 4 | УОНМ, УЗИМ | ИРД, СР |
| 02, 05, 06, 12.05 |
|
| 96 | §43 | Исследование квадратного трехчлена | 1 | УОНМ, УЗИМ | ИРК |
| 13.05 |
|
| 97 |
| Решение задач. Подготовка к контрольной работе | 1 | УОСЗ, УПЗУ | ДСР |
| 16.05 |
|
| 98 |
| Контрольная работа №5 «Квадратные неравенства» | 1 | УКЗУ | КР | 1 | 19.05 |
|
| 99–101 |
| Повторение. Решение задач | 4ч | УПЗУ, УЗИМ, УОСЗ | СРЗ, ИЗ | 1 | 20, 26, 27.05 |
|
| 102 |
| Итоговая контрольная работа | 1 | УКЗУ | КР | 1 | 23.05 |
|
ТРЕБОВАНИЯ К УРОВНЮ
ПОДГОТОВКИ ВЫПУСКНИКОВ
В результате изучения математики ученик должен
знать/понимать1
существо понятия математического доказательства; приводить примеры доказательств;
существо понятия алгоритма; приводить примеры алгоритмов;
как используются математические формулы, уравнения и неравенства; примеры их применения для решения математических и практических задач;
как математически определенные функции могут описывать реальные зависимости; приводить примеры такого описания;
как потребности практики привели математическую науку к необходимости расширения понятия числа;
вероятностный характер многих закономерностей окружающего мира; примеры статистических закономерностей и выводов;
каким образом геометрия возникла из практических задач землемерия; примеры геометрических объектов и утверждений о них, важных для практики;
смысл идеализации, позволяющей решать задачи реальной действительности математическими методами, примеры ошибок, возникающих при идеализации;
Алгебра
Уметь
составлять буквенные выражения и формулы по условиям задач; осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления, осуществлять подстановку одного выражения в другое; выражать из формул одну переменную через остальные;
выполнять основные действия со степенями с целыми показателями, с многочленами и с алгебраическими дробями; выполнять разложение многочленов на множители; выполнять тождественные преобразования рациональных выражений;
применять свойства арифметических квадратных корней для вычисления значений и преобразований числовых выражений, содержащих квадратные корни;
решать линейные, квадратные уравнения и рациональные уравнения, сводящиеся к ним, системы двух линейных уравнений и несложные нелинейные системы;
решать линейные и квадратные неравенства с одной переменной и их системы;
решать текстовые задачи алгебраическим методом, интерпретировать полученный результат, проводить отбор решений, исходя из формулировки задачи;
изображать числа точками на координатной прямой;
определять координаты точки плоскости, строить точки с заданными координатами; изображать множество решений линейного неравенства;
распознавать арифметические и геометрические прогрессии; решать задачи с применением формулы общего члена и суммы нескольких первых членов;
находить значения функции, заданной формулой, таблицей, графиком по ее аргументу; находить значение аргумента по значению функции, заданной графиком или таблицей;
определять свойства функции по ее графику; применять графические представления при решении уравнений, систем, неравенств;
описывать свойства изученных функций, строить их графики;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
выполнения расчетов по формулам, составления формул, выражающих зависимости между реальными величинами; нахождения нужной формулы в справочных материалах;
моделирования практических ситуаций и исследования построенных моделей с использованием аппарата алгебры;
описания зависимостей между физическими величинами соответствующими формулами при исследовании несложных практических ситуаций;
интерпретации графиков реальных зависимостей между величинами.
Материально-техническое обеспечение
Дидактический материал:
индивидуальные карточки по всем темам учебного курса;
карточки для проведения самостоятельных работ;
карточки для проведения контрольных работ;
карточки для проведения зачетных уроков;
| Контрольные работы | Самостоятельные работы, тесты, практические работы |
| № | Тема | № | Тема |
| 1 | Входная контрольная работа | 1 | Положительные и отрицательные числа |
| 2 | № 1: «Неравенства» | 2 | Числовые неравенства. Основные свойства числовых неравенств |
| 3 | № 2: «Квадратные корни» | 3 | Неравенства с одним неизвестным. Решение неравенств |
| 4 | № 3: «Квадратные уравнения» | 4 | Решение систем неравенств |
| 5 | № 4: «Квадратичная функция» | 5 | Модуль числа. Уравнения и неравенства, содержащие модуль |
| 6 | № 5: «Квадратные неравенства» | 6 | Приближенные значения величин. Погрешность приближения |
| 7 | Итоговая контрольная работа | 7 | Арифметический квадратный корень |
|
|
| 8 | Квадратный корень из степени |
|
|
| 9 | Квадратный корень из произведения |
|
|
| 10 | Квадратный корень из дроби |
|
|
| 11 | Квадратный корень из произведения и из дроби |
|
|
| 12 | Неполные квадратные уравнения |
|
|
| 13 | Решение квадратных уравнений |
|
|
| 14 | Приведенное квадратное уравнение. Теорема Виета |
|
|
| 15 | Решение задач с помощью квадратных уравнений |
|
|
| 16 | Решение простейших систем, содержащих уравнение второй степени |
|
|
| 17 | Функция y = x2 |
|
|
| 18 | Функция y = ax2 + bx + c |
|
|
| 19 | Построение графика квадратичной функции |
|
|
| 20 | Квадратное неравенство и его решение |
|
|
| 21 | Решение квадратного неравенства с помощью графика квадратичной функции |
|
|
| 22 | Метод интервалов |
|
|
| 23 | Исследование квадратичной функции |
Оборудование: компьютер, экран, мультимедийный проектор, линейка, транспортир, треугольник, циркуль
Наглядный материал: таблицы, презентации, интерактивная доска, учебные диски
Учебно-методический комплект
ОСНОВНАЯ УЧЕБНО-МЕТОДИЧЕСКАЯ ЛИТЕРАТУРА
Алгебра. 8 класс: учебник для общеобразовательных учреждений. / [Ш.А. Алимов, Ю.М. Колягин, Ю.В. Сидоров, М.В. Ткачева, Н.Е. Федорова, М.И. Шабунин] – М.: Просвещение, 2011
Программы общеобразовательных учреждений: Алгебра. 7 – 9 классы /Составитель Т.А. Бурмистрова – учебное издание. – М: Просвещение,2008
Стандарт основного общего образования по математике /Математика в школе. – 2004г, – №4. – с.4
ДОПОЛНИТЕЛЬНАЯ УЧЕБНО-МЕТОДИЧЕСКАЯ ЛИТЕРАТУРА
Алгебра. 8 класс: Поурочные планы по учебнику Ш.А. Алимова и др. /Автор-составитель Е.Г. Лебедева. – Волгоград: Учитель, 2006
Алгебра. 8 класс: дидактические материалы. /Составители М.К. Потапов, А.В. Шевкин. – М.: Просвещение, 2007
Дидактические материала по алгебре для 8 класса /В.И. Жохов, Ю.Н. Макарычев, Н.Г. Миндюк. – М.: Просвещение, 1995
Математика: самостоятельные и контрольные работы. 7 – 9 классы. /А.П. Ершова, В.В. Голобородько. – М.: Илекса, 2001
Разноуровневые дидактические материалы по алгебре. 8 класс. /М.Б. Миндюк, Н.Г. Миндюк. – М.: Генжер, 2002
Математика. Карточки для коррекции знаний. 8 класс. /Г.Г. Левитас. – М.: Илекса, 2000
Контрольные и проверочные работы по алгебре. 7 – 9 классы. /Л.И. Звавич, Л.Я. Шляпочник. – М.: Дрофа, 1998
Алгебра. Тесты. 7 – 9 классы: учебно-методическое пособие. /П.И. Алтынов. – М.: Дрофа, 2001
Уроки алгебры в 8 классе. Пособие для учителей. /В.И. Жохов, Л.Б. Крайнева. – М.: Вербум, 2000
Е.Б. Арутюнян, М.Б. Волович и др. Математические диктанты для 5 – 9 классов. – М: Просвещение, 1991
Тесты. Математика. 5 – 11 классы. – М.: ООО «Агентство «КРПА «Олимп»: ООО «Издательство АСТ», 2002
Интернет-ресурсы
Тестирование online: 5 – 11 классы: http://www.kokch/kts.ru/cdo
Педагогическая мастерская, уроки в Интернет и многое другое: http://teacyer.fio.ru
Новые технологии в образовании: http://www.edu.sekna.ru/main
Путеводитель «В мире науки» для школьников: http://www.uic.ssu.samara.ru/-nauka
Математические этюды: http://www.etudes.ru
Министерство образования РФ: http://www.ed.gov.ru/ ; http://www.edu.ru
Сеть творческих учителей: http://it-n.ru/communities.aspx?cat_no=4510&tmpl=com
Мегаэнциклопедия Кирилла и Мефодия: http://mega.km.ru
Сайты «Энциклопедий»: http://www.rubricon.ru/; http://www.encyclopedia.ru
Сайт для самообразования и online тестирования: http://uztest.ru/
Досье школьного учителя математики: http://www.mathvaz.ru/
Единая коллекция цифровых образовательных ресурсов: http://school-collection.edu.ru/
Учитель: ____________________ Бякина Л.Н.
1 Помимо указанных в данном разделе знаний, в требования к уровню подготовки включаются также знания, необходимые для освоения перечисленных ниже умений.

 Получите свидетельство
Получите свидетельство Вход
Вход











 Рабочая программа по математике (8 класс) (0.39 MB)
Рабочая программа по математике (8 класс) (0.39 MB)
 0
0 540
540 9
9 Нравится
0
Нравится
0







