17
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Рабочая программа составлена в соответствии на основе:
Федеральный закон Российской Федерации «Об образовании в Российской Федерации» (№ 273-ФЗ от 29.12.2012)
Федеральный государственный образовательный стандарт основного общего образования / Министерство образования и науки РФ.— М.: Просвещение, 2011. (Стандарты второго поколения.) Приказ Министерства образования и науки РФ от 17.12.2010. № 1897
Примерные программы основного общего образования. Математика. Проект – 3-е изд. – М.: Просвещение, 2011 (Стандарты второго поколения)
Примерная программа конкретизирует содержание предметных тем образовательного стандарта и даёт примерное распределение учебных часов по разделам курса.
Изучение математики в 6 классе направлено на реализацию целей и задач, сформулированных в Государственном стандарте общего образования по математике:
овладение системой математических знаний и умений, необходимых для применения в практической деятельности, продолжения образования;
интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе, ясность и точность мысли, интуиция, логическое мышление, элементы алгоритмической культуры, пространственных представлений, способность к преодолению трудностей;
формировать представление об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;
воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, понимание значимости математики для научно-технического прогресса.
В ходе преподавания математики в 6 классе, работы над формированием у учащихся перечисленных в программе знаний и умений, следует обращать внимание на то, чтобы они овладевали умениям и навыками общеучебного характера, разнообразными способами деятельности, приобретали опыт:
планирования и осуществления алгоритмической деятельности, выполнения заданных и конструирования новых алгоритмов;
решения разнообразных классов задач из различных разделов курса, в том числе задач, требующих поиска пути и способов решения;
исследовательской деятельности, развития идей, проведения экспериментов, обобщения, постановки и формулирования новых задач;
ясного, точного, грамотного изложения своих мыслей в устной и письменной речи, использования различных языков математики (словесного, символического, графического), свободного перехода с одного языка на другой для иллюстрации, интерпретации, аргументации и доказательства;
проведения доказательных рассуждений, аргументации, выдвижения гипотез и их обоснования;
поиска, систематизации, анализа и классификации информации, использования разнообразных информационных источников, включая учебную и справочную литературу, современные информационные технологии.
Рабочая программа основного общего образования по математике для 6 класса составлена на основе Фундаментального ядра содержания общего образования и требований к результатам освоения основной общеобразовательной программы основного общего образования, представленных в Федеральном государственном образовательном стандарте второго поколения. В них также учитываются основные идеи и положения Программы развития и формирования универсальных учебных действий для основного общего образования.
Сознательное овладение учащимися системой арифметических знаний и умений в повседневной жизни, для изучения смежных дисциплин и продолжения образования.
Практическая значимость школьного курса математики 6 класса обусловлена тем, что её объектом являются количественные отношения действительного мира. Математическая подготовка необходима для понимания принципов устройства и использования современной техники, восприятия научных и технологических понятий и идей. Математика является языком науки и техники. С её помощью моделируются явления и процессы, происходящие в природе.
Арифметика является одним из опорных предметов основной школы: она обеспечивает изучение других дисциплин. В первую очередь это относится к предметам естественно-научного цикла. Развитие логического мышления учащихся при обучении математике в 6 классе способствует усвоению предметов гуманитарного цикла. Практические умения и навыки арифметического характера необходимы для трудовой и профессиональной подготовки школьников.
Развитие у учащихся правильных представлений о сущности и происхождении арифметических абстракций. О соотношении реального и идеального, о характере отражения математической наукой явлений и процессов реального мира, о месте арифметики в системе наук и роли математического моделирования в научном познании и в практике способствует формированию научного мировоззрения учащихся, а также формированию качеств мышления, необходимых для адаптации в современном информационном обществе.
Требуя у учащихся умственных и волевых усилий, концентрации внимания, активности, воображения, арифметика развивает нравственные черты личности (настойчивость, целеустремленность, творческую активность, самостоятельность, ответственность, трудолюбие, дисциплину и критичность мышления) и умение аргументировано отстаивать свои взгляды и убеждения, а также способность принимать самостоятельные решения. Активное использование и решение текстовых задач на всех этапах учебного процесса развивают творческие способности школьников.
Изучение математики в 6 классе позволяет формировать умения и навыки умственного труда: планирование своей работы поиск рациональных путей её выполнения, критическую оценку результатов. В процессе изучения математики школьники учатся излагать свои мысли ясно и исчерпывающе, лаконично и ёмко, приобретают навыки чёткого, аккуратного и грамотного выполнения математических записей.
Важнейшей задачей школьного курса арифметики является развитие логического мышления учащихся. Сами объекты математических умозаключений и принятые в арифметике правила их конструирования способствуют формированию умений обосновывать и доказывать суждения, приводить чёткие определения, развивают логическую интуицию, кратко и наглядно раскрывают механизм логических построений и учат их применению. Показывая внутреннюю гармонию математики, формируя понимание красоты и изящества математических рассуждений, арифметика вносит значительный вклад в эстетическое воспитание учащихся.
В курсе математики 6 класса можно выделить следующие основные содержательные линии: арифметика, элементы алгебры, вероятность и статистика, наглядная геометрия. Наряду с этим в содержание включены две дополнительные методологические темы: множества и математика в историческом развитии, что связано с реализацией целей общеинтеллектуального и общекультурного развития учащихся. Содержание каждой из этих тем разворачивается в содержательно-методическую линию, пронизывающую все основные содержательные линии. При этом первая линия – «Множества» - служит цели овладения учащимися некоторыми элементами универсального математического языка, вторая – «Математика в историческом развитии» - способствует созданию общекультурного, гуманитарного фона изучения курса.
Содержание линии «Арифметика» служит фундаментом для дальнейшего изучения учащимися математики и смежных дисциплин, способствует развитию не только вычислительных навыков, но и логического мышления, формированию умения пользоваться алгоритмами, способствует развитию умений планировать и осуществлять деятельность, направленную на решение задач, а также приобретению практических навыков, необходимых в повседневной жизни.
РАСПРЕДЕЛЕНИЕ КУРСА ПО ТЕМАМ.
В связи с расхождением в распределении тем, изучаемых в 6 классах школ Крыма и РФ (2013-2014 уч. г), возникает необходимость выделения 45 ч (за счет уменьшения часов на изучение других тем) для изучения тем: « Делимость натуральных чисел» -14ч, « Обыкновенные дроби» -26ч. На повторение материала за 6 класс отведено 7ч.
В школах Крыма из раздела «Десятичные дроби» в 5классе были изучены темы:
а) «Сравнение положительных десятичных дробей»,
б) «Сложение и вычитание десятичных дробей»,
в) «Умножение и деление десятичных дробей», поэтому на изучение раздела
«Десятичные дроби» выделено 15ч.
| № п/п. | Наименование разделов и тем
| Всего часов |
| 1. | Повторение | 5 |
| 2 | Делимость натуральных чисел | 14 |
| 3 | Обыкновенные дроби | 26 |
| 4. | Отношения, пропорции, проценты | 22 |
| 5. | Целые числа | 28 |
| 6. | Рациональные числа | 34 |
| 7. | Десятичные дроби | 15 |
| 8. | Обыкновенные и десятичные дроби | 19 |
| 9. | Повторение | 7 |
|
| Итого | 170 |
Требования к уровню подготовки учащихся 6 класса в соответствии с Государственным образовательным стандартом
В результате изучения курса математики в 6 классе учащиеся должны знать/понимать:
существо понятия алгоритма;
как используются математические формулы и уравнения при решении математических и практических задач;
как потребности практики привели математическую науку к необходимости расширения понятия числа;
каким образом геометрия возникла из практических задач землемерия;
уметь:
выполнять действия сложения и вычитания, умножения и деления с рациональными числами, возводить рациональное число в квадрат, в куб;
переходить от одной формы записи чисел к другой, представлять десятичную дробь в виде обыкновенной и обыкновенную в виде десятичной, проценты в виде дроби и дробь в виде процентов;
находить значение числовых выражений;
решать задачи на проценты с помощью пропорций; применять прямо и обратно пропорциональные величины при решении практических задач; решать задачи на масштаб;
распознавать и изображать перпендикулярные и параллельные прямые с помощью линейки и угольника; определять координаты точки на координатной плоскости, отмечать точки по заданным координатам;
решать текстовые задачи арифметическим способом и с помощью уравнений, включая задачи, связанные с дробями и процентами;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни:
для решения несложных практических задач, в том числе с использованием справочных материалов, калькулятора, компьютера;
устной прикидки и оценки результатов вычислений; проверки результатов вычислений с использованием различных приемов;
интерпретации результатов решения задач с учетом ограничений, связанных с реальными свойствами рассматриваемых процессов и явлений.
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
решения несложных практических расчетных задач, в том числе c использованием при необходимости справочных материалов, калькулятора, компьютера;
устной прикидки и оценки результата вычислений; проверки результата вычисления, с использованием различных приемов;
интерпретации результатов решения задач с учетом ограничений, связанных с реальными свойствами рассматриваемых процессов и явлений.
выполнения расчетов по формулам, для составления формул, выражающих зависимости между реальными величинами; для нахождения нужной формулы в справочных материалах;
моделирования практических ситуаций и исследовании построенных моделей с использованием аппарата математики;
описания зависимостей между физическими величинами соответствующими формулами, при исследовании несложных практических ситуаций.
МЕСТО ПРЕДМЕТА В УЧЕБНОМ ПЛАНЕ
Согласно федеральному базисному учебному плану на изучение математики в 6 классе отводится не менее 170 часов из расчета 5 ч в неделю (34 рабочих недели).
ОБЩАЯ ХАРАКТЕРИСТИКА КУРСА
Делимость натуральных чисел
Свойства и признаки делимости. Простые и составные числа. Делители натурального числа. Наибольший общий делитель, наименьшее общее кратное.
Основная цель – познакомить обучающихся со свойствами и признаками делимости, сформировать навыки их использования.
Отношения, пропорции, проценты
Отношение чисел и величин. Масштаб. Деление числа в заданном отношении. Пропорции. Прямая и обратная пропорциональность. Понятие о проценте. Задачи на проценты. Круговые диаграммы. Задачи на перебор всех возможных вариантов. Вероятность события.
Основная цель – восстановить навыки работы с натуральными и рациональными числами, усвоить понятия, связанные с пропорциями и процентами.
Целые числа
Отрицательные целые числа. Противоположное число. Модуль числа. Сравнение целых чисел. Сложение целых чисел. Законы сложения целых чисел. Разность целых чисел. Произведение целых чисел. Частное целых чисел. Распределительный закон. Раскрытие скобок и заключение в скобки. Действия с суммами нескольких слагаемых. Представление целых чисел на координатной оси.
Основная цель – научить учащихся работать со знаками, так как арифметические действия над их модулями – натуральными числами – уже хорошо усвоены.
Рациональные числа
Отрицательные дроби. Рациональные числа. Сравнение рациональных чисел. Сложение и вычитание дробей. Умножение и деление дробей. Законы сложения и умножения. Смешанные дроби произвольного знака. Изображение рациональных чисел на координатной оси. Уравнения. Решение задач с помощью уравнений.
Основная цель – добиться осознанного владения школьниками арифметических действий над рациональными числами.
Десятичные дроби
Понятие положительной десятичной дроби. Сравнение положительных десятичных дробей. Сложение и вычитание десятичных дробей. Перенос запятой в положительной десятичной дроби. Умножение положительных десятичных дробей. Деление положительных десятичных дробей. Десятичные дроби и проценты. Десятичные дроби любого знака. Приближение десятичных дробей. Приближение суммы, разности, произведения и частного двух чисел.
Основная цель – научить учащихся действиям с десятичными дробями и приближёнными вычислениями.
Обыкновенные и десятичные дроби
Разложение положительной обыкновенной дроби в конечную десятичную дробь. Бесконечные периодические десятичные дроби. Непериодические бесконечные периодические десятичные дроби. Длина отрезка. Длина окружности. Площадь круга. Координатная ось. Декартова система координат на плоскости. Столбчатые диаграммы и графики.
Основная цель – ввести действительные числа.
ТРЕБОВАНИЯ К РЕЗУЛЬТАТАМ ОБУЧЕНИЯ И ОСВОЕНИЮ СОДЕРЖАНИЯ КУРСА
Программа позволяет добиваться следующих результатов освоения образовательной программы основного общего образования:
личностные:
ответственного отношения к учению, готовности и способности обучающихся к саморазвитию и самообразованию на основе мотивации к обучению и познанию;
формирования коммуникативной компетентности в отношении и сотрудничестве со сверстниками, старшими и младшими в образовательной, учебно-исследовательской, творческой и других видах деятельности;
умения ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи, встраивать аргументацию, приводить примеры и контр примеры;
первоначального представления о математической науке как сфере человеческой деятельности, об этапах её развития, о её значимости для развития цивилизации;
критичности мышления, умения распознавать логически некорректные высказывания, отличать гипотезу от факта;
креативности мышления, инициативности, находчивости, активности при решении арифметических задач;
умения контролировать процесс и результат учебной математической деятельности;
формирования способности к эмоциональному восприятию математических объектов, задач, решений, рассуждений;
метапредметные:
способности самостоятельно планировать альтернативные пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач;
умения осуществлять контроль по образцу и вносить необходимые коррективы;
способности адекватно оценивать правильность или ошибочность выполнения учебной задачи, её объективную трудность и собственные возможности её решения;
умения устанавливать причинно-следственные связи; строить логические рассуждения, умозаключения и выводы;
умения создавать, применять и преобразовывать знаково-символические средства, модели и схемы для решения учебных и познавательных задач;
развития способности организовывать с учителем и сверстниками: определять цели, распределять функции и роли участников, взаимодействовать и находить общие способы решения; умения работать в группе: находить общее решение и разрешать конфликты на основе согласования позиций и учёта интересов; слушать партнёра; формулировать, аргументировать и отстаивать своё мнение;
формирования учебной и общепользовательской компетентности в области использования информационно-коммуникационных технологий (ИКТ-компетентности);
первоначального представления об идеях и о методах математики как об универсальном языке науки и техники;
развития способности видеть математическую задачу и других дисциплинах, в окружающей жизни;
умения находить в разных источниках информацию, необходимую для решения математических проблем, и представлять её в понятной форме; принимать решение в условиях неполной и избыточной, точной и вероятностной информации;
Умения понимать и использовать математические средства наглядности для иллюстрации, интерпретации, аргументации;
Умения выдвигать гипотезы при решении учебных задач и понимания необходимости их проверки;
Понимания сущности алгоритмических предписаний и умения действовать в соответствии с предложенным алгоритмом;
Способности планировать и осуществлять деятельность, направленную на решение задач исследовательского характера;
предметные:
умения работать с математическим текстом, точно и грамотно выражать свои мысли в устной и письменной речи, применяя математическую терминологию и символику, использовать различные языки математики, развития способности обосновывать суждения, проводить классификацию;
владения базовым понятийным аппаратом: иметь представление о числе, дроби, процентах, об основных геометрических объектах, формирования представлений о статистических закономерностях в реальном мире и различных способах их изучения;
умения выполнять арифметические преобразования рациональных выражений, применять их для решения учебных математических задач и задач, возникающих в смежных учебных предметах;
умения пользоваться изученными математическими формулами;
знания основных способов представления и анализа статистических данных; умения решать задачи с помощью перебора всех возможных вариантов;
умения применять изученные понятия, результаты и методы при решении задач из различных разделов курса, в том числе задач, не сводящихся к непосредственному применению известных алгоритмов.
ПЛАНИРУЕМЫЕ РЕЗУЛЬТАТЫ ИЗУЧЕНИЯ
Делимость натуральных чисел
Знать:
Понятия: простые и составные числа, делители натурального числа; наибольший общий делитель; взаимно простые числа; кратное натуральных чисел; наименьшее общее кратное
Свойства делимости и признаки делимости на 10, 5, 2, 9,3; правила делимости суммы и разности чисел.
Уметь:
Использовать: свойства и признаки делимости при доказательстве делимости натуральных чисел и числовых выражений;
Пользоваться: таблицей простых чисел; для рационализации вычислений: правилами делимости суммы и разности чисел;
Находить: делители натурального числа, наибольший общий делитель, кратные числа, наименьшее общее кратное; является число простым или составным;
Отношения, пропорции, проценты
Усвоить основное свойство пропорции.
Уметь решать несложные задачи с помощью пропорций.
Познакомиться с понятиями и формулами длины окружности и площади круга.
Уметь решать задачи с помощью пропорций на проценты.
Уметь решать практические задачи на прямую и обратную пропорциональную зависимости.
Целые числа
Знать:
Понятия целого числа, его модуля, законы сложения и умножения.
Уметь:
Выполнять действия с целыми числами, находить его модуль, использовать законы сложения и умножения при решении упражнений.
Рациональные числа
Ученик научится:
понимать особенности десятичной системы счисления;
выражать числа в эквивалентных формах, выбирая наиболее подходящую в зависимости от конкретной ситуации;
сравнивать и упорядочивать рациональные числа;
выполнять вычисления с рациональными числами, сочетая устные и письменные приёмы вычислений, применение калькулятора;
использовать понятия и умения, связанные с пропорциональностью величин, процентами в ходе решения математических задач и задач из смежных предметов, выполнять несложные практические расчёты.
Ученик получит возможность:
углубить и развить представление о свойствах делимости;
научиться использовать приёмы, рационализирующие вычисления, приобрести привычку контролировать вычисления, вытирая подходящий для ситуации способ.
Десятичные дроби
Ученик научится:
использовать начальные представления о множестве действительных чисел.
Ученик получит возможность:
развивать представление о числе и числовых системах от натуральных до действительных чисел; о роли вычислений в человеческой практике;
развить и углубить знания о десятичной записи действительных чисел (периодические и непериодические дроби).
Обыкновенные дроби
Знать:
что означает обыкновенной дроби; основное свойство дроби; правильная дробь меньше единицы, неправильная дробь больше единицы, делить на ноль нельзя; операция деления обратная умножению; смешанная дробь это другая запись неправильной дроби, порядок выполнения действий.
Понятия: обыкновенная дробь, числитель, знаменатель, рациональное число, равные дроби, правильная и неправильная дробь, несократимая дробь, сократимая дробь, общий знаменатель, дополнительный множитель, обратная дробь, взаимно обратные дроби, производительности, смешанной дроби, целой и дробной частей смешанной дроби , симметрия относительно плоскости.
Правила: сложения, вычитания, умножения, деления всех видов дробей, умножения натурального числа на дробь, деления дроби на натуральное число;
Законы: сложения , умножения, распределительный закон;
Уметь:
сокращать дроби, записывать дробь равную данной, проводить дроби к общему знаменателю, сравнивать дроби всех видов, приводить дроби к общему знаменателю, выполнять все арифметические действия с дробями всех видов, превращать правильную дробь в неправильную, выделять целую часть у неправильной дроби, различать фигуры симметричные относительно плоскости.
решать задачи: находить часть от числа, нахождение числа по его части, на совместную работу, на движение по реке;
использовать для рационализации вычислений: законы сложения, умножения, распределительный закон,
изображать: дроби всех видов на координатном луче.
НОРМЫ ОЦЕНКИ ЗНАНИЙ, УМЕНИЙ И НАВЫКОВ УЧАЩИХСЯ ПО МАТЕМАТИКЕ
Критерии оценивания тестовых работ обучающихся
Отметка «5» ставится, если выполнено 91-100% работы.
Отметка «4» ставится, если выполнено 75-90% работы.
Отметка «3» ставится, если выполнено 50-74% работы.
Отметка «2» ставится, если выполнено 20-49% работы.
Отметка «1» ставится, если выполнено менее 20% работы.
Критерии оценивания устных ответов обучающихся
Отметка «5» ставится, если ученик:
полно раскрыл содержание материала в объеме, предусмотренном программой и учебником;
изложил материал грамотным языком, точно используя математическую терминологию и символику, в определенной логической последовательности;
правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;
показал умение иллюстрировать теорию конкретными примерами, применять ее в новой ситуации при выполнении практического задания;
продемонстрировал знание теории ранее изученных сопутствующих тем, сформированность и устойчивость используемых при ответе умений и навыков;
отвечал самостоятельно, без наводящих вопросов учителя;
возможны одна – две неточности при освещение второстепенных вопросов или в выкладках, которые ученик легко исправил после замечания учителя.
Отметка «4» ставится, если ответ удовлетворяет в основном требованиям на оценку «5», но при этом имеет один из недостатков:
в изложении допущены небольшие пробелы, не исказившее математическое содержание ответа;
допущены один – два недочета при освещении основного содержания ответа, исправленные после замечания учителя;
допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в выкладках, легко исправленные после замечания учителя.
Отметка «3» ставится в следующих случаях:
неполно раскрыто содержание материала (содержание изложено фрагментарно, не всегда последовательно), но показано общее понимание вопроса и продемонстрированы умения, достаточные для усвоения программного материала (определены «Требованиями к математической подготовке учащихся» в настоящей программе по математике);
имелись затруднения или допущены ошибки в определении математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;
ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;
при достаточном знании теоретического материала выявлена недостаточная сформированность основных умений и навыков.
Отметка «2» ставится в следующих случаях:
не раскрыто основное содержание учебного материала;
обнаружено незнание учеником большей или наиболее важной части учебного материала;
допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.
Отметка «1» ставится, если:
ученик обнаружил полное незнание и непонимание изучаемого учебного материала или не смог ответить ни на один из поставленных вопросов по изученному материалу.
Критерии оценивания контрольных и самостоятельных работ обучающихся
Отметка «5» ставится, если:
работа выполнена полностью;
в логических рассуждениях и обосновании решения нет пробелов и ошибок;
в решении нет математических ошибок (возможна одна неточность, описка, которая не является следствием незнания или непонимания учебного материала).
Отметка «4» ставится в следующих случаях:
работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);
допущены одна ошибка или есть два – три недочёта в выкладках, рисунках, чертежах или графиках (если эти виды работ не являлись специальным объектом проверки).
Отметка «3» ставится, если:
Отметка «2» ставится, если:
Отметка «1» ставится, если:
Общая классификация ошибок
При оценке знаний и умений и навыков учащихся следует учитывать все ошибки (грубые и негрубые) и недочеты.
Грубыми считаютсяо шибки:
незнание определения основных понятий, законов, правил, основных положений, теорий, незнание формул, общепринятых символов обозначений величин, единиц их измерения;
незнание наименований единиц измерения;
неумение выделять в ответе главное;
неумение применять знания, алгоритмы для решения задач;
неумение делать выводы и обобщения;
неумение читать и строить графики;
неумение пользоваться первоисточниками, учебником, справочником;
потеря корня или сохранение постороннего корня;
отбрасывание без объяснений одного из них;
равнозначные им ошибки;
вычислительные ошибки, если они не являются опиской;
логические ошибки.
К негрубым ошибкам следует отнести:
неточность формулировок, определений, понятий, теорий, вызванная не полнотой охвата основных признаков определяемого понятия или заменой одного – двух из этих признаков второстепенными;
неточность графика;
нерациональный метод решения задачи или недостаточно продуманный план ответа (нарушение логики, подмена отдельных основных вопросов второстепенными);
нерациональные методы работы со справочником и другой литературой;
неумение решать задачи, выполнять задания в общем виде.
Недочетами являются:
нерациональное применение вычислений, преобразований;
небрежное выполнение записей, чертежей, схем, графиков.
КОНТРОЛЬ УРОВНЯ ОБУЧЕННОСТИ.
Контроль за результатами обучения осуществляется через использование следующих видов контроля: входной, текущий, тематический, итоговый. При этом используются различные формы контроля: контрольная работа, домашняя контрольная работа, самостоятельная работа, домашняя практическая работа, домашняя самостоятельная работа, тест, контрольный тест, устный опрос, блиц-опрос, фронтальный опрос, теоретический опрос, математический диктант.
Промежуточная аттестация проводится в соответствии с Уставом образовательного учреждения в форме годовых контрольных работ.
Принятые обозначения
ДР- диагностическая контрольная работа
КР – контрольная работа;
СР – самостоятельная работа;
ПР – проверочная работа;
КТ – контрольный тест;
Т – тестовая работа
ФО – фронтальный опрос.
УО – устный опрос
БО- блиц опрос.;
ДКР – домашняя контрольная работа;
ТО – теоретический опрос;
МД – математический диктант
Тематическое планирование и характеристика основных видов деятельности ученика
| Основное содержание по темам | Характеристика основных видов деятельности ученика (на уровне учебных действий) |
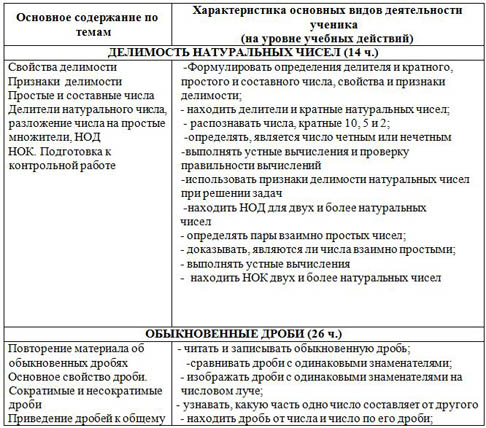
| ДЕЛИМОСТЬ НАТУРАЛЬНЫХ ЧИСЕЛ (14 ч.) |
| Свойства делимости Признаки делимости Простые и составные числа Делители натурального числа, разложение числа на простые множители, НОД НОК. Подготовка к контрольной работе | -Формулировать определения делителя и кратного, простого и составного числа, свойства и признаки делимости; - находить делители и кратные натуральных чисел; - распознавать числа, кратные 10, 5 и 2; - -определять, является число четным или нечетным - -выполнять устные вычисления и проверку правильности вычислений - -использовать признаки делимости натуральных чисел при решении задач -находить НОД для двух и более натуральных чисел - определять пары взаимно простых чисел; - доказывать, являются ли числа взаимно простыми; - выполнять устные вычисления - находить НОК двух и более натуральных чисел -
|
| ОБЫКНОВЕННЫЕ ДРОБИ (26 ч.) |
| Повторение материала об обыкновенных дробях Основное свойство дроби. Сократимые и несократимые дроби Приведение дробей к общему знаменателю Сложение и вычитание дробей с разными знаменателями Сложение и вычитание смешанных чисел. Произведение дробей. Умножение дроби на число, взаимнообратные дроби. Возведение дроби в степень. Законы умножения. Умножение смешанных чисел. Деление дробей, деление на натуральное число. Нахождение части целого и целого по его части. Деление смешанных чисел. | - читать и записывать обыкновенную дробь; -сравнивать дроби с одинаковыми знаменателями; - изображать дроби с одинаковыми знаменателями на числовом луче; - узнавать, какую часть одно число составляет от другого - находить дробь от числа и число по его дроби; -приводить дроби к общему знаменателю; - находить дополнительный множитель; - приводить дроби к общему знаменателю с применением разложения их знаменателей на простые множители; - находить наименьший общий знаменатель (НОЗ) дробей -применять правило при сравнении дробей; - читать координаты отмеченных на луче точек; - приводить с подробным рассуждением примеры сравнения дробей - складывать дроби с разными знаменателями, используя правило; - доказывать неравенство; - представлять выражение в виде дроби; - использовать переместительный и сочетательный законы сложения при вычислениях - вычитать дроби с разными знаменателями, используя правило; - применять правила умножения дробей при вычислениях - применять свойства умножения при нахождении значения выражений с дробями - применять правило деления дробей при решении уравнений, решении текстовых задач; - решать задачи на нахождение целого от числа и части числа по его целому - представлять смешанное число в виде суммы целой и дробной частей; - представлять смешанное число в виде неправильной дроби; - выделять целую часть из неправильной дроби - складывать смешанные числа; - вычитать смешанные числа; - складывать и вычитать смешанные числа, применяя известные свойства сложения и вычитания; -выполнять умножение и деление дробей и смешанных чисел;
|
| ОТНОШЕНИЯ, ПРОПОРЦИИ, ПРОЦЕНТЫ. (22 ч.) |
| Отношения чисел и величин Масштаб Деление числа в данном отношении Пропорции Прямая и обратная пропорциональность Повторение материала о процентах, задачи на проценты. Круговые диаграммы |
- строить круговые диаграммы, изображающие распределение отдельных составных частей какой-либо величины; понимать круговые диаграммы |
| ЦЕЛЫЕ ЧИСЛА (28 ч.) |
| Отрицательные целые числа Противоположные числа, модуль числа Сравнение целых чисел Сложение целых чисел, законы сложения Разность целых чисел Подготовка к контрольной работе Произведения целых чисел Частное целых чисел Распределительный закон Раскрытие скобок и заключение скобок Действия суммами нескольких слагаемых Представление целых чисел на координатной оси | - приводить примеры использования в окружающем мире положительных и отрицательных чисел (температура, выигрыш-проигрыш, выше ниже уровня моря и т. п.); - изображать точками координатной прямой положи тельные и отрицательные рациональные числа; - характеризовать множество целых чисел, множество рациональных чисел. - сравнивать и упорядочивать рациональные числа, выполнять вычисления с рациональными числами; - формулировать и записывать с помощью букв свойства сложения и вычитания положительных и отрицательных чисел; - формулировать и записывать с помощью букв свойства действий с рациональными числами, применять для преобразования числовых выражений;
|
| РАЦИОНАЛЬНЫЕ ЧИСЛА (34 ч.) |
| Отрицательные дроби Рациональные числа Сравнение рациональных чисел Сложение и вычитание дробей Умножение и деление дробей Законы сложения и умножения Смешанные дроби произвольного знака Изображение рациональных чисел на координатной оси Уравнения Решения задач с помощью уравнений | - составлять уравнения по условию задачи, по рисунку; - проверять, является ли данное число корнем уравнения; - решать уравнения, зная правила нахождения компонентов действий сложения и вычитания; - проверять правильность решения - вычислять числовое значение буквенного выражения при заданных значениях букв; - составлять уравнения по условиям задач; - решать простейшие уравнения на основе зависимостей между компонентами арифметических действий. - строить на координатной плоскости точки и фигуры по заданным координатам, определять координаты точек; - извлекать информацию из таблиц и диаграмм, выполнять вычисления по табличным данным, сравнивать величины, находить наибольшие и наименьшие значения и др.
|
| ДЕСЯТИЧНЫЕ ДРОБИ (15 ч.) |
| Систематизация знаний учащихся о десятичных дробях Десятичные дроби и проценты Десятичные дроби произвольного знака Приближение десятичных дробей Приближение суммы, разности, произведения и частного двух чисел. |
- записывать и читать десятичные дроби, представлять обыкновенную дробь в виде десятичной и наоборот, называть целую и дробную части десятичных дробей; - уравнивать количество знаков в дробной части числа; - сравнивать десятичные дроби. Сравнивать десятичные дроби, а также значения величин различных единиц измерений. - округлять десятичные дроби до заданного разряда; - складывать и вычитать десятичные дроби.
|
| ОБЫКНОВЕННЫЕ, ДЕСЯТИЧНЫЕ ДРОБИ (19 ч) |
| Разложение положительной обыкновенной дроби в конечную десятичную дробь. Бесконечные периодические периодичные дроби Непериодические бесконечные десятичные дроби Длина отрезка Длина окружности, площадь круга. Координатная ось Декартовая система координат на плоскости Столбчатые диаграммы и графики |
-изображать и обозначать отрезки, измерять их длины и строить отрезки заданной длины с помощью линейки; - изображать координатный луч; - изображать окружность данного радиуса с помощью циркуля; распознавать точки, принадлежащие окружности
|
УЧЕБНО- МЕТОДИЧЕСКОЕ И Материально-техническое обеспечение образовательного процесса
Литература:
Учебник «Математика» для 6 класса общеобразовательных учреждений – М.: «Просвещение», 2014г, С.М. Никольский и др.
Образовательные электронные ресурсы:
1)Математика. Первое сентября [Электронный ресурс]//http://mat.1september.ru
2) Математика в школе [Электронный ресурс] //http://www.школьная пресса.рф
3) http://www.school.edu.ru/ -Российский образовательный портал
4) http://www.1september.ru/ - газета «Первое сентября»
5) http://all.edu.ru/ - Все образование Интернета
6) http://school-collection.edu.ru/ - единая коллекция цифровых образовательных ресурсов.

 Получите свидетельство
Получите свидетельство Вход
Вход











 Рабочая программа по математике (6 класс ФГОС) (62.13 КB)
Рабочая программа по математике (6 класс ФГОС) (62.13 КB)
 0
0 929
929 188
188 Нравится
0
Нравится
0



