Правила. №607(2,4),613(2),585,612Правила. №607(2,4),613(2),585,612Муниципальное автономное общеобразовательное учреждение города Калининграда лицей № 18
РАБОЧАЯ ПРОГРАММА
по математике
5 КЛАСС
Линия учебников Г.К.Муравина, К.С.Муравина, О.В.Муравиной
Составлена: Почетухина Елена Александровна
|
|
РАССМОТРЕНА на заседании предметной кафедры математики Протокол №__от «__»____20__г. Руководитель кафедры_________ _________________И. В. Дымова |
УТВЕРЖДЕНА на заседании научно-методического совета МАОУ лицея №18 Протокол №___от « __»______20__г. Зам. директора по НМР________________Н.П.Гуменюк
|
ВВЕДЕНА В ДЕЙСТВИЕ Приказом от «__»______20___г. Директор МАОУ лицея №18 ________________И.А.Теличко
|
|
|
|
|
|
2012-2013 учебный год
пояснительная записка
Введение
Рабочая программа по математике разработана на основе Федерального государственного образовательного стандарта основного общего образования1, Концепции духовно-нравственного развития и воспитания личности гражданина России2, примерных программ основного общего образования3.
Рабочая программа по математике для 5 классов содержит:
1) пояснительную записку, в которой конкретизируются общие цели основного общего образования с учётом специфики учебного предмета математика и возраста обучающихся;
2) общую характеристику учебного предмета математика для 5 класса;
3) описание места учебного предмета математика в учебном плане;
4) личностные, метапредметные и предметные результаты освоения математики в 5 классе;
5) содержание учебного предмета математика;
6) тематическое планирование с определением основных видов учебной деятельности;
7) описание учебно-методического и материально-технического обеспечения образовательного процесса;
8) планируемые результаты изучения математики.
1.2. Конкретизация общих целей основного общего образования в рабочей программе
Рабочая программа нацелена на продолжение формирования у обучающихся 5 классов начатых в начальной школе основ теоретического мышления: произвольности учебных действий, анализа, планирования, рефлексии, а также - на развитие логики и математической интуиции.
Кроме того, значительное внимание программа уделяет созданию условий для осознания обучающимися значения математики в повседневной жизни человека, для формирования у них представлений о математике как универсальном научном языке, позволяющем изучать и описывать реальные процессы и явления в жизни человека. Практическая часть данной программы содержит проектные задачи - однопредметные и межпредметные, - решая которые, школьники учатся применять математические знания в квази-реальной ситуации.
Систематически применяемая проектная методика позволяет учителю включать обучающихся в проблемно-ценностные дискуссии, формирующие у младших подростков уважительное и доброжелательное отношение к другому человеку, его мировоззрению, гражданской позиции, к общечеловеческим и национальным ценностям, а также - готовность и способность действовать сообща на основе взаимопонимания.
Специально организуемая в ходе изучения математики контрольно-оценочная деятельность пятиклассников призвана развивать у них такие важные качества как самостоятельность, ответственность, способность к инициативному действию.
Таким образом, рабочая программа по математике нацелена на дальнейшее комплексное формирование у обучающихся предметных, метапредметных и личностных образовательных результатов.
1.3. Общая характеристика учебного предмета математика для 5 класса
В программе реализуется концепция развивающего обучения, которая предусматривает особую организацию учебной деятельности обучающихся: математическое содержание развертывается в теоретической форме - от общего к частному, от абстрактного к конкретному. При этом знания не даются учителем в готовом виде (в виде образцов, правил, алгоритмов), а добываются обучающимися при решении учебной задачи (учебной проблемы) путем выполнения самостоятельных учебных действий.
В курсе математики 5 классов можно выделить две относительно самостоятельные содержательные линии. Первая, арифметическая, касается развития понятия числа. Вторая связана с формированием геометрических представлений. Кроме того, в программу органично включен материал, знакомящий обучающихся с логикой и множествами, а также - математикой в историческом развитии4.
Укрупнение дидактической единицы позволяет следующим образом классифицировать учебный материал арифметической линии:
Натуральные числа и нуль
Доли и дроби
Обыкновенные дроби
Десятичные дроби
Характерной особенностью обучения математике в 5 классе становится усиление роли моделирования. При этом модели приобретают качественно новый характер по сравнению с моделированием в начальной школе: из средства фиксации способов, открытых в предметном плане, они сами становятся источником постановки учебных задач и тем самым - открытия новых способов действия.
Геометрическая линия в значительной степени связана с изучением величин и действий с ними, с построением идеальных геометрических образов и развитием пространственных представлений. Одной из особенностей разворачивания геометрического материала является конструктивный подход к геометрическим понятиям, который самым естественным образом приводит к большому числу задач на построение геометрических фигур. Таким образом, так же как и арифметической линии, при формировании понятий основополагающую роль играют предметные действия обучающихся.
Большая роль в рабочей программе отведена проектным задачам, в которых интегрируются все основные содержательные линии, изучаемые в 5 классе. Под проектной задачей мы понимаем задачу, в которой через систему заданий целенаправленно стимулируется система детских действий, направленных на получение еще никогда не существовавшего в практике ребенка результата («продукта»). Отличие проектной задачи от проекта заключается в том, что для решения этой задачи пятиклассникам предлагаются все необходимые средства и материалы. Проектная задача учит их способу проектирования через специально разработанные учителем задания по осуществлению «переноса» известных им предметных способов действий в квазиреальную, модельную ситуацию, где эти способы изначально скрыты, а иногда и требуют переконструирования. Проектная задача учит пятиклассников:
рефлексировать (видеть проблему; анализировать сделанное – почему получилось, почему не получилось; видеть трудности, ошибки);
целеполагать (ставить и удерживать цели);
планировать (составлять план своей деятельности);
моделировать (представлять способ действия в виде схемы-модели, выделяя все существенное и главное);
проявлять инициативу при поиске способа (способов) решения задач;
вступать в коммуникацию (взаимодействовать при решении задачи, отстаивать свою позицию, принимать или аргументировано отклонять точки зрения других).
Основными инструментами оценки в рамках решения проектных задач являются экспертные карты (оценка процесса решения) и экспертные оценки по заданным критериям предъявления выполненных «продуктов». Как итог учебного года для учителя важна динамика становления класса как учебного сообщества, развития способностей детей ставить задачи, искать пути их решения. На этапе решения проектных задач главной является оценка процесса (процесса решения, процесса предъявления результата) и только потом оценка самого результата.
Проектная задача во многих случаях реализуется в форме разновозрастного учебного сотрудничества пятиклассников с младшими или старшими школьниками: 2 или 8 классы. В первом случае пятиклассники выступают в позиции «учителя», что становится важным фактором формирования у них учебной самостоятельности и способности к инициативному действию. Реализуя возникшее в этом возрасте "чувство взрослости", они учатся понимать и учитывать интеллектуальную и эмоциональную позицию другого человека, начинают по новому видеть труд собственных учителей. Отвечая притязаниям младших подростков на равноправные, ответственные, «серьезные» отношения с миром взрослых, работа в позиции «учителя» служит одной из мер профилактики подросткового негативизма в его школьных проявлениях (дисциплинарных, учебных, мотивационных).
Учебное сотрудничество между пятиклассниками и более старшими ребятами дает возможность учителю организовать образовательный процесс в пятом классе так, чтобы пятиклассники, инициативно выстраивая учебные отношения с восьмиклассниками, могли бы сами определить границы своих знаний и построить собственные «карты» движения в учебном материале
1.4. Место учебного предмета математика в учебном плане
Математика считается ведущим предметом в системе естественно-математического образования пятиклассников. При проектировании и реализации решения проектных задач межпредметного содержания этому предмету отводится центральное место в условиях координации предметов биология, география, химия, физика.
В системе учебного плана время на изучение математики в 5 классе увеличено до 6 часов в неделю за счет вариативного компонента, всего 136 часов. За счет этого увеличения учителю предоставлена возможность для интенсификации образовательного процесса и индивидуализации учебной деятельности посредством активного применения технологии педагогического сопровождения индивидуальных образовательных маршрутов обучающихся: индивидуализированных домашних работ практического и творческого содержания, в том числе - с использованием интернет-ресурсов, решения проектных задач.
Организация учебной деятельности по математике в рамках данной рабочей программы осуществляется как через уроки, так и через внеурочные формы:
| Урочные формы учебной деятельности | Внеурочные формы учебной деятельности |
общеклассная дискуссия – коллективно-распределённая деятельность в ходе постановки и решения учебных задач, при моделировании общего способа действия; презентация – публичное предъявление обучающимся на уроке результата ("продукта") индивидуализированной домашней работы; контрольные виды деятельности - диагностическая, проверочная, контрольная работы; постановка однопредметной проектной задачи. | консультация – учитель работает с группой обучающихся по их запросу; лаборатория - особая форма консультации при решении проектной задачи; мастерская – индивидуальная работа с обучающимся по устранению учебных дефицитов (с активным применением ресурса разновозрастного сотрудничества); решение однопредметной или межпредметной проектной задачи; тренинг - решение обучающимся частно-практических задач по опробованию изученного способа действия с использованием интернет-ресурса. |
1.5. Личностные, метапредметные и предметные результаты освоения математики в 5 классе
Программа предполагает достижение пятиклассниками следующих личностных, метапредметных и предметных результатов.
В личностных результатах сформированность:
– самостоятельности и ответственного отношения к учению на основе развитой мотивации к учебной деятельности, заинтересованность в приобретении и расширении математических знаний и способов действий, осознанность построения индивидуального образовательного маршрута в предмете;
– коммуникативных навыков в рамках содержательного общения в группе при решении учебных и проектных задач, умение вести конструктивный диалог, понимать и уважать позицию собеседника, достигать взаимопонимания, сотрудничать для достижения общих результатов;
– понимания изучаемых математических понятий и владение способами действия, умение применять их в квазиреальных ситуациях;
– логического мышления: критичности (умение распознавать логически некорректные высказывания), креативности (собственная аргументация, опровержения, постановка задач, формулировка проблем, исследовательский проект и др.).
В метапредметных результатах сформированность:
– способности самостоятельно ставить цели учебной и исследовательской деятельности, планировать, осуществлять, контролировать и оценивать учебные действия в соответствии с поставленной задачей и условиями ее выполнения;
– умения самостоятельно планировать альтернативные пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач;
- умения находить необходимую информацию в различных источниках (в справочниках, литературе, Интернете), представлять информацию в различной форме (словесной, табличной, графической, символической), обрабатывать, хранить и передавать информацию в соответствии с познавательными или коммуникативными задачами;
– владения приемами умственных действий: определения понятий, обобщения, установления аналогий, классификации на основе самостоятельного выбора оснований и критериев, установления родовидовых и причинно-следственных связей, построения умозаключений индуктивного, дедуктивного характера или по аналогии;
– умения организовывать совместную учебную деятельность с учителем и сверстниками: определять цели, распределять функции, взаимодействовать в группе, выдвигать гипотезы, находить решение проблемы, разрешать конфликты на основе согласования позиции и учета интересов, аргументировать и отстаивать свое мнение
В предметных результатах сформированность:
– умений работать с математическим текстом, точно и грамотно выражать свои мысли в устной и письменной речи, применяя математическую терминологию и символику, использовать различные языки математики (словесный, символический, графический, табличный), доказывать математические утверждения;
– умения использовать базовые понятия из основных разделов содержания (число, уравнение, неравенство, вероятность, множество, доказательство и др.);
– представлений о числе и числовых системах от натуральных до действительных чисел; практических навыков выполнения устных, письменных, инструментальных вычислений, вычислительной культуры;
– представлений о простейших геометрических фигурах, пространственных телах и их свойствах; и умений в их изображении;
– умения измерять длины отрезков, величины углов, использовать формулы для нахождения периметров, площадей и объемов простейших геометрических фигур;
– умения использовать символьный язык алгебры, приемы тождественных преобразований рациональных выражений, решения уравнений, неравенств и их систем; идею координат на плоскости для интерпретации решения уравнений, неравенств и их систем; алгебраического аппарата для решения математических и нематематических задач;
–– представлений о статистических закономерностях в реальном мире и о различных способах их изучения, об особенностях выводов и прогнозов, носящих вероятностный характер;
– приемов владения различными языками математики (словесный, символический, графический) для иллюстрации, интерпретации, аргументации и доказательства;
– умения применять изученные понятия, аппарат различных разделов курса к решению межпредметных задач и задач повседневной жизни.
II. СОДЕРЖАНИЕ УЧЕБНОГО ПРЕДМЕТА МАТЕМАТИКА
Натуральные числа. Натуральный ряд. Десятичная система счисления. Арифметические действия над натуральными числами. Степень с натуральным показателем.
Числовые выражения, значение числового выражения. Порядок действий в числовых выражениях со скобками и без скобок. Решение текстовых задач арифметическими способами. Законы арифметических действий: переместительные, сочетательные, распределительные. Степень с целым показателем.
Делители и кратные. Деление с остатком. Измерения, приближения, оценки. Единицы измерения длины, площади, объема, массы, времени, скорости. Размеры объектов окружающего мира (от элементарных частиц до Вселенной), длительность процессов в окружающем нас мире.
Выделение множителя – степени десяти в записи числа.
Приближенное значение величины, точность приближения. Округление натуральных чисел и десятичных дробей. Прикидка и оценка результатов вычислений.
Дроби. Обыкновенные дроби. Основное свойство дроби. Сравнение дробей. Арифметические действия с обыкновенными дробями. Нахождение части от целого и целого по его части.
Десятичные дроби. Сравнение десятичных дробей. Арифметические действия с десятичными дробями. Представление десятичной дроби в виде обыкновенной дроби и обыкновенной в виде десятичной.
Проценты. Нахождение процентов от величины, величины по ее процентам. Отношение. Выражение отношения в процентах. Пропорция. Основное свойство пропорции.
Решение текстовых задач на проценты.
Теоретико-множественные понятия. Множество, элемент множества. Задание множеств перечислением элементов, характеристическим свойством. Стандартные обозначения числовых множеств. Пустое множество и его обозначение. Подмножество. Объединение и пересечение множеств.
Элементы логики. Определения и теоремы. Доказательство. Доказательство от противного. Теорема, обратная данной. Пример и контрпример.
Математика в историческом развития. История формирования понятия числа: натуральные числа, дроби,. Старинные системы записи чисел. Дроби в Вавилоне, Египте, Риме, Индии, на Руси. Открытие десятичных дробей. Старинные системы мер. Десятичные дроби и метрическая система мер. История появления процентов. С. Стевин, ал-Каши, Л. Ф. Магницкий. История развития справочных таблиц по математике.
Зарождение алгебры в недрах арифметики. Ал-Хорезми. Рождение буквенной символики. П. Ферма, Ф. Виет, Р. Декарт. История вопроса о нахождении формул корней алгебраических уравнений. Диофант, Л. Фибоначчи, М. Штифель, Ф. Виет.
История развития геометрии. Пифагор, Геродот, Фалес. Нахождение объемов тел. Архимед, И. Ньютон, Г. Лейбниц.
Приближенные вычисления. А. Н. Крылов.
Геометрический материал знакомит школьников с основными понятиями геометрии, которые затем будут активно использоваться в систематическом курсе.
III. ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ С ОПРЕДЕЛЕНИЕМ ОСНОВНЫХ ВИДОВ УЧЕБНОЙ ДЕЯТЕЛЬНОСТИ
3.1. Учебно-тематический план
| Перечень разделов, тем | Количество часов | Разбивка часов по видам занятий |
| Теоретические виды занятий | Практические виды занятий | Контрольные работы (ч) |
| Обобщение и систематизация материала.
| 3 | 1 | 1 | 1 |
| Натуральные числа и нуль. Практикум, учебные исследовательские проекты. | 35
| 6
| 27
| 2 |
| Числовые и буквенные выражения. Практикум, учебные исследовательские проекты. | 37
| 5
| 30
| 2
|
| Доли и дроби. Практикум, учебные исследовательские проекты.
| 19 | 3 | 15 | 1 |
| Действия с дробями. Практикум, учебные исследовательские проекты. | 36 | 6 | 28 | 2 |
| Десятичные дроби. Практикум, учебные исследовательские проекты. | 54 | 10 | 40 | 4 |
| Повторение.
| 20 | 3 | 16 | 1 |
| Итого | 204 | 34 | 157 | 13 |
3.2. Календарно-тематическое планирование с конкретизацией основных видов учебной деятельности
|
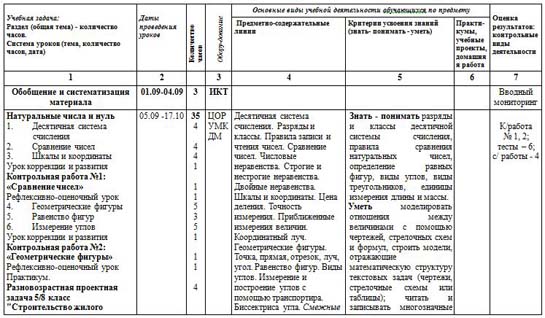
Учебная задача: Раздел (общая тема) - количество часов. Система уроков (тема, количество часов, дата) |
Даты проведения уроков | Количество часов |
Обору-дование | Основные виды учебной деятельности обучающихся по предмету |
Оценка результатов: контрольные виды деятельности |
| Предметно-содержательные линии | Критерии усвоения знаний (знать- понимать - уметь)
| Практи-кумы, учебные проекты, домашняя работа |
| 1 | 2 |
| 3 | 4 | 5 | 6 | 7 |
| Обобщение и систематизация материала | 01.09-04.09 | 3 | ИКТ |
|
|
| Вводный мониторинг |
| Натуральные числа и нуль Десятичная система счисления Сравнение чисел Шкалы и координаты Урок коррекции и развития Контрольная работа №1: «Сравнение чисел» Рефлексивно-оценочный урок Геометрические фигуры Равенство фигур Измерение углов Урок коррекции и развития Контрольная работа №2: «Геометрические фигуры» Рефлексивно-оценочный урок Практикум. Разновозрастная проектная задача 5/8 класс "Строительство жилого комплекса "Семья" | 05.09 -17.10 | 35 4
4 4 1
1 1 5 3 5 1
1 1
4 | ЦОР УМК ДМ | Десятичная система счисления. Разряды и классы. Правила записи и чтения чисел. Сравнение чисел. Числовые неравенства. Строгие и нестрогие неравенства. Двойные неравенства. Шкалы и координаты. Цена деления. Точность измерения. Приближенные измерения величин. Координатный луч. Геометрические фигуры. Точка, прямая, отрезок, луч, угол. Равенство фигур. Виды углов. Измерение и построение углов с помощью транспортира. Биссектриса угла. Смежные и вертикальные углы. Окружность, центр, радиус и диаметр окружности. Параллельные и перпендикулярные прямые. Ломаная, многоугольник, периметр многоугольника. Треугольник. Виды треугольников. Неравенство треугольника.
| Знать - понимать разряды и классы десятичной системы счисления, правила сравнения натуральных чисел, определение равных фигур, виды углов, виды треугольников, единицы измерения длины и массы. Уметь моделировать отношения между величинами с помощью чертежей, стрелочных схем и формул, строить модели, отражающие математическую структуру текстовых задач (чертежи, стрелочные схемы или таблицы); читать и записывать многозначные числа; снимать показания приборов, переводить из одних единиц измерения длины и массы в другие, выполнять все арифметические действия с многозначными числами. Исследовать простейшие числовые закономерности, проводить числовые эксперименты (в том числе с использованием калькулятора, компьютера) |
|
К/работа № 1, 2; тесты – 6; с/ работы - 4 |
| Числовые и буквенные выражения Числовые выражения и их значения Площадь прямоугольника Объём прямоугольного параллелепипеда Урок коррекции и развития Контрольная работа №3: «Числовые выражения» Рефлексивно-оценочный урок Буквенные выражения Формулы и уравнения Урок коррекции и развития Контрольная работа № 4: «Числовые и буквенные выражения» Рефлексивно-оценочный урок Практикум. Межпредметная проектная задача "Строительство детской площадки"( координация с предметами география, биология, литература, информатика, ИЗО)
|
18.10-05.12
| 37
6 6
4 1
1 1 6 5 1
1
1
4 | УМКДМ, ИКТ | Числовые выражения. Значение числового выражения. Действия с натуральными числами. Деление с остатком. Решение текстовых задач с помощью составления числовых выражений. Площадь прямоугольника. Степень числа. Порядок действий в выражениях, содержащих степень числа. Плоские и объемные фигуры. Прямоугольный параллелепипед и пирамида. Вершины, грани, ребра. Объем прямоугольного параллелепипеда. Буквенные выражения. Числовое значение буквенного выражения. Законы арифметических действий. Формулы и уравнения. Вычисление по формуле. Решение линейных уравнений на основе взаимосвязи между компонентами и результатами арифметических действий. Решение текстовых задач с помощью линейных уравнений.
| Знать - понимать связь отношений между величинами в соответствии с соответствующими арифметическими действиями и применять их для решения текстовых задач и уравнений; законы арифметических действий и применять эти знания для вычисления значений выражений, формулы периметра прямоугольника и квадрата, площади прямоугольника и квадрата, объёма прямоугольного параллелепипеда, формулы стоимости, пути и работы, определения уравнения, корня уравнения, что значит решить уравнение.
Уметь различать и читать числовые и буквенные выражения, применять законы арифметических действий для рационализации вычислений, переводить из одних единиц измерения площади и объема в другие, применять формулы для решения текстовых задач, решать задачи на движение двух объектов, решать уравнения на основе зависимости между компонентами действий, решать текстовые задачи с помощью составления линейных уравнений. |
| к/ работа №3,4 тесты – 7; с/ работы - 6 |
| Доли и дроби. Понятие о долях и дробях Сложение и вычитание дробей с равными знаменателями. Умножение дроби на натуральное число. Урок коррекции и развития Контрольная работа №5 «Доли и дроби» Рефлексивно-оценочный урок. Треугольники Практикум. Разновозрастная проектная задача 2/5 класс "Как измерить всё на свете" |
06.12-29.12
| 19 6
3
1
1 1 3
4 | УМКДМ, ИКТ | Обыкновенная дробь. Правильные и неправильные дроби. Площадь прямоугольного и произвольного треугольника. Сумма углов треугольника. Теорема Пифагора.
| Знать понятия: доля, дробь, числитель дроби, знаменатель дроби, правильная и неправильная дроби, правила сравнения обыкновенных дробей с помощью координатного луча, сравнение дробей с равными знаменателями или равными числителями, приведением дробей к общему знаменателю. Уметь моделировать в графической, предметной форме понятия и свойства, связанные с понятием дроби. Изображать обыкновенную дробь на числовой прямой, сравнивать обыкновенные дроби и смешанные числа, решать текстовые задачи на нахождение части от числа и числа по его части. Проводить несложные исследования, связанные со свойствами дробных чисел, опираясь на числовые эксперименты (в том числе с использованием калькулятора, компьютера) |
| К / работа №5 тесты – 3, с/ работы - 2 |
| Действия с дробями Дробь как результат деления натуральных чисел Деление дроби на натуральное число. Основное свойство дроби. Сравнение дробей Урок коррекции и развития Контрольная работа №6 «Основное свойство дроби» Рефлексивно-оценочный урок. Сложение и вычитание дробей Умножение на дробь Деление на дробь Урок коррекции и развития. Контрольная работа №7 «Действия с дробями» Рефлексивно-оценочный урок. Практикум. Ситуативная однопредметная проектная задача"Встречаем гостей" |
11.01-22.02
| 36
5
4
3 1
1 1 4 4 6 1 1
1
4 | УМКДМ, ИКТ | Основное свойство дроби. Приведение дробей к общему знаменателю. Сокращение дробей. Сравнение дробей. Арифметические действия с обыкновенными дробями. Основные задачи на дроби. Обыкновенная дробь как отношение величинРациональное число. Изображение рациональных чисел на числовой прямой Смешанное число как описание способа измерения величины.
| Знать - понимать основное свойство дроби, правила арифметических действий с обыкновенными дробями и смешанными числами, типы задач на части. Уметь переводить неправильные дроби в смешанные числа и наоборот, выполнять все арифметические действия с обыкновенными дробями и смешанными числами, решать текстовые задачи на части. Анализировать и осмысливать текст задачи, переформулировать условие, моделировать условие с помощью схем, рисунков, реальных предметов; строить логическую цепочку рассуждений; критически оценивать полученный ответ, осуществлять самоконтроль, проверяя ответ на соответствие условию.
|
|
к/работы №6,7 – 2, тесты – 5, с/ работы - 6 |
| Десятичные дроби. Понятие десятичной дроби Сравнение десятичных дробей Сложение и вычитание десятичных дробей Урок коррекции и развития Контрольная работа №8 «Сложение и вычитание десятичных дробей» Рефлексивно-оценочный урок Умножение десятичных дробей Деление десятичной дроби на натуральное число Урок коррекции и развития Контрольная работа №9 «Деление и умножение десятичных дробей» Рефлексивно-оценочный урок. Бесконечные десятичные дроби Округление чисел Деление на десятичную дробь. Урок коррекции и развития Контрольная работа №10 «Действия с дробями»» Рефлексивно-оценочный урок. Процентные расчёты Среднее арифметическое чисел Урок коррекции и развития Контрольная работа № 11 «Проценты» Рефлексивно-оценочный урок Практикум. Разновозрастные проектные задачи (целевые группы): 5/8 класс"Школа ремонта", 2/5 класс "Прогулка с невидимками"(целое и части)
|
25.02-06.05
| 54 3 4
4 1
1
1
5
4 1 1
1 2
3 3 1
1 1 6 4
1
1 1
4 | УМКДМ, ИКТ | Понятие десятичной дроби. Сравнение десятичных дробей. Определение расстояния между точками на координатном луче. Перевод обыкновенной дроби в десятичную и десятичной в обыкновенную. Округление десятичных дробей. Периодические десятичные дроби. Арифметические действия с десятичными дробями. Совместные вычисления с обыкновенными и десятичными дробями. Среднее арифметическое двух и более чисел. Проценты. Основные задачи на проценты. | Знать - понимать определение десятичной дроби, правило чтения и записи десятичных дробей, правило сравнения десятичных дробей, правила действий с десятичными дробями, правило округления десятичных дробей, определение процента, понятие среднего арифметического нескольких чисел. Уметь: изображать позиционные дроби на числовой прямой, сравнивать дроби, читать, записывать, округлять десятичные дроби, выполнять все действия с десятичными дробями, перевести десятичную дробь в обыкновенную и смешанное число и наоборот, решать основные задачи на проценты,находить среднее арифметическое нескольких чисел. Осуществлять поиск информации (в СМИ), содержащей данные, выраженные в процентах, интерпретировать их. Приводить примеры использования отношений в практике. |
|
к/работы №8, 9, 10, 11– 4, тесты – 9, с/работы - 9 |
| Повторение. Натуральные числа и нуль. Обыкновенные дроби. Десятичные дроби. Межпредметная проектная задача "Гуси-лебеди" (координация с предметами география, биология, физика, химия, литература, информатика)
| 07.05-30.05 | 20 4 6 6 4 | УМКДМ ЦОР | Знать: правила вычислений с натуральными, обыкновенными и десятичными дробями; правила сравнения натуральных чисел, обыкновенных и десятичных дробей; определение уравнения; основное свойство дроби; свойства арифметических действий; формулы периметра прямоугольника (квадрата), площади прямоугольника (квадрата), объема прямоугольного параллелепипеда (куба), пути, стоимости, работы; единицы измерения длины, массы, времени, площади, объема, скорости. Уметь: выполнять устно арифметические действия: сложения и вычитания двузначных чисел и десятичных дробей с двумя знаками, умножение однозначных чисел, арифметические операции с обыкновенными дробями с однозначным знаменателем и числителем; переходить от одной записи чисел к другой, представлять десятичную дробь в виде обыкновенной и в простейших случаях обыкновенную в виде десятичной; представлять проценты в виде дроби и дроби в виде процентов; записывать многозначные натуральные числа в виде разложения по степеням числа 10; находить значение числовых выражений;
6округлять целые числа и десятичные дроби; находить приближения чисел с недостатком и избытком; выполнять оценку значений числовых выражений; находить среднее арифметическое нескольких чисел; изображать натуральные числа, обыкновенные дроби, десятичные дроби на координатном луче; определять координаты точек на координатном луче, строить точки с заданными координатами; решать линейные уравнения с помощью зависимостей между компонентами действий; пользоваться основными единицами длины, массы, времени, скорости, площади, объема; выражать единицы через мелкие и наоборот; решать текстовые задачи арифметическим способом и с помощью простейших уравнений; решать текстовые задачи на части и проценты; составлять буквенные выражения и формулы по условиям задач; осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления, выражать из формул одну величину через остальные; строить и измерять отрезки с помощью линейки, углы с помощью транспортира; строить параллельные и перпендикулярные прямые с помощью линейки и угольника, окружности с помощью циркуля | ДКР презентации | Итоговый мониторинг |
3.3. Описание учебно-методического и материально-технического обеспечения образовательного процесса
| Наименование объектов и средств материально-технического обеспечения | Примечания |
| Программы |
| Рабочая программа курса математики для 5-9 классов общеобразовательных учреждений / Сост. О.В.Муравина.– М.: Дрофа, 2011. | В программе определены цели и задачи курса, рассмотрены особенности содержания и результаты его освоения (личностные, метапредметные и предметные); представлены содержание основного общего образования по математике, тематическое планирование с характеристикой основных видов деятельности учащихся, описано материально-техническое обеспечение образовательного процесса |
| Учебники |
| Муравин Г.К., Муравина О.В. Математика. 5 класс. Учебник. – М.: Дрофа, 2011. Муравин Г.К., Муравина О.В. Математика. 6 класс. Учебник. – М.: Дрофа, 2011.
| В учебниках реализована главная цель, которую ставили перед собой авторы – развитие личности школьника средствами математики, подготовка его к продолжению обучения и к самореализации в современном обществе. В учебниках представлен материал, соответствующий программе и позволяющий учащимся 5-6 классов выстраивать индивидуальные траектории изучения математики за счет обязательного и дополнительного материала, маркированной разноуровневой системы упражнений, организованной помощи в разделе «Ответы, советы и решения», дополнительного материала: различных практикумов, исследовательских и практических работ, домашних контрольных работ, исторического и справочного материала и др. |
| Рабочие тетради |
| Муравин Г.К., Муравина О.В. Математика. 5 класс. Рабочая тетрадь. В 2 ч. . – М.: Дрофа, 2011. Муравин Г.К., Муравина О.В. Математика. 6 класс. Рабочая тетрадь. В 2 ч. – М.: Дрофа, 2011.
| Рабочие тетради предназначены для организации самостоятельной деятельности учащихся. В них представлена система разнообразных заданий для закрепления знаний и отработки универсальных учебных действий. Задания в тетрадях располагаются в соответствии с содержанием учебников. Тетради также содержат вычислительные практикумы и контрольные задания в формате ЕГЭ ко всем главам учебника |
| Дидактические материалы |
| Муравин Г.К., Муравина О.В. Математика. 5-6 классы. Дидактические материалы. – М.: Дрофа, 2010. А.П. Ершова, В.В. Голобородько. Самостоятельные и контрольные работы по математике для 5 класса. – М.: Илекса, 2003.
| Дидактические материалы обеспечивают диагностику и контроль качества обучения в соответствии с требованиями к уровню подготовки учащихся, закрепленными в стандарте. Пособия содержат проверочные работы: тесты, самостоятельные и контрольные работы, дополняют задачный материал учебников и рабочих тетрадей, содержит ответы ко всем заданиям Сборники заданий |
| Дополнительная литература для учащихся |
| Башмаков М.И. Математика в кармане «Кенгуру». Международные олимпиады школьников. – М.: Дрофа, 2011. Звавич Л.И., Рязановский А.Р. Алгебра в таблицах. 7-11 классы. Справочное пособие. – М.: Дрофа, 2011. Коликов А.Ф., Коликов А.В. Изобретательность в вычислениях. – М.: Дрофа, 2009. Математика в формулах. 5-11 классы. Справочное пособие. – М.: Дрофа, 2011. Петров В.А. Математика. 5-11 классы. Прикладные задачи. – М.: Дрофа, 2010. Шарыгин И.Ф. Уроки дедушки Гаврилы, или Развивающие каникулы. – М.: Дрофа, 2010. | Список дополнительной литературы необходим учащимся для лучшего понимания идей математики, расширения спектра изучаемых вопросов, углубления интереса к предмету, а также для подготовки докладов, сообщений, рефератов, творческих работ, проектов и др. В список вошли справочники, учебные пособия, сборники олимпиад, книги для чтения и др.
|
| Методические пособия для учителя |
| Муравин Г.К., Муравина О.В. Математика. 5 класс. Методическое пособие. В 2 ч. – М.: Дрофа, 2007. Муравин Г.К., Муравина О.В. Математика. 6 класс. Методическое пособие. – М.: Дрофа, 2010. А.В. Шевкин. Обучение решению текстовых задач в 5-6 классах. Книга для учителя. – М.: Галс, 1998.
| В методических пособиях описана авторская технология обучения математике. Пособия построены поурочно и включают примерное тематическое планирование, самостоятельные и контрольные работы, математические диктанты, тесты, задания для устной работы и дополнительные задания к уроку, инструкции по проведению зачетов, решения задач на смекалку и для летнего досуга |
| Печатные пособия |
| Комплект таблиц по математике. 5-6 классы. 8 двусторонних таблиц Комплект портретов для кабинета математики (15 портретов) | Комплекты таблиц справочного характера охватывают основные вопросы по математике каждого года обучения. Таблицы помогут не только сделать процесс обучения более наглядным и эффективным, но и украсят кабинет математики. Таблицы содержат правила действий с числами, таблицы метрических мер, основные математические формулы, соотношения, законы, графики функций. В комплекте портретов для кабинета математики представлены портреты математиков, вклад которых в развитие математики представлен в ФГОС |
| Компьютерные и информационно-коммуникативные средства обучения |
| СD-ROM «Математика. 5-11 классы» СD-ROM «Интерактивная математика». 5-9 классы. СD-ROM «Вероятность и статистика» 5-9 классы. Практикум СD-ROM «Математика. 5 класс». Мультимедийное приложение к учебнику СD-ROM «Математика. 6 класс». Мультимедийное приложение к учебнику
| Мультимедийные обучающие программы носят проблемно-тематический характер и обеспечивают дополнительные условия для изучения отдельных тем и разделов математики. Диски разработаны для самостоятельной работы учащихся на уроках (если класс оснащен компьютерами) или в домашних условиях. Материал по основным вопросам математики основной школы представлен на дисках в трех аспектах: демонстрации по содержанию предмета, практикумы по решению задач, работы для самоконтроля уровня усвоения знаний |
| Электронные образовательные ресурсы |
| uchportal.ru alleng.ru school-collektion.edu.ru. muravin2007.narod.ru mathematika-na.ru |
| Технические средства |
| Персональный компьютер с принтером Мультимедиапроектор с экраном или интерактивная доска Ксерокс Принтер |
| УЧЕБНО-ПРАКТИЧЕСКОЕ И УЧЕБНО-ЛАБОРАТОРНОЕ ОБОРУДОВАНИЕ |
| Аудиторная доска с магнитной поверхностью и набором приспособлений для крепления таблиц Комплект инструментов классных: линейка, транспортир, угольник (300, 600), угольник (450, 450), циркуль Комплект стереометрических тел (демонстрационный и раздаточный) Набор планиметрических фигур |
3.4. Планируемые результаты изучения математики
В результате изучения тем курса математики 5 класса обучающиеся должны:
способность выявлять отношения между величинами в предметных ситуациях и в ситуациях, описанных в текстах; представлять выделенные отношения в виде различных моделей (знаковых, графических); решать задачи на различные отношения межу величинами;
описывать свойства натурального ряда, читать и записывать натуральные числа, находить сумму цифр числа и сумму разрядных слагаемых;
сравнивать и упорядочивать натуральные числа;
различать и называть равенства и неравенства, строгие и нестрогие неравенства, двойные неравенства;
опровергать утверждения с помощью контрпримера;
читать и записывать единицы измерения длины и массы, снимать показания приборов;
выражать одни единицы измерения длины и массы в других единицах;
строить на координатном луче точки по заданным координатам; определять координаты точек;
различать и называть геометрические фигуры: точка, прямая, отрезок, луч, угол, прямоугольник, квадрат, многоугольник, окружность;
распознавать на чертежах, рисунках в окружающем мире геометрические фигуры, конфигурации фигур (плоские, пространственные), приводить примеры аналогов геометрических фигур в окружающем мире;
изображать геометрические фигуры и их конфигурации от руки и с использованием чертежных инструментов, изображать геометрические фигуры на клетчатой бумаге;
находить и называть равные фигуры, осуществлять построение равных фигур с помощью кальки;
исследовать и описывать свойства диагоналей прямоугольника, используя эксперимент, наблюдение, измерение, моделирование;
решать задачи на нахождение длин отрезков, периметров многоугольников;
измерять с помощью инструментов и сравнивать величины углов;
строить с помощью транспортира углы заданной величины;
находить на рисунке смежные и вертикальные углы;
исследовать сумму углов в треугольнике, используя эксперимент, наблюдение, измерение, моделирование;
вычислять значения степеней, находить значение числового выражения, содержащего степени чисел;
вычислять площади квадратов и прямоугольников, используя формулы площади квадрата и прямоугольника; выражать одни единицы измерения площади через другие;
решать задачи на нахождение площадей квадратов и прямоугольников;
исследовать площадь прямоугольников с заданным периметром;
читать и записывать числовые выражения;
исследовать простейшие числовые закономерности, проводить числовые эксперименты;
изготавливать пространственные тела из разверток; распознавать развертки куба, параллелепипеда, пирамиды, цилиндра и конуса;
соотносить пространственные фигуры с их проекциями на плоскость;
вычислять объемы куба и прямоугольного параллелепипеда, используя формулы объема куба и прямоугольного параллелепипеда, выражать одни единицы измерения объема через другие;
читать и записывать буквенные выражения, составлять буквенные выражения по условиям задач, вычислять числовое значение буквенного выражения при заданных значениях букв;
моделировать несложные зависимости с помощью формул; выполнять вычисления по формулам, использовать знания о зависимостях между величинами (скорость, время, расстояние; работа, производительность, время и т.п.) при решении текстовых задач, составлять буквенные выражения по условиям задач;
составлять уравнения по условиям задач, решать простейшие уравнения на основе зависимостей между компонентами действий;
анализировать текст задачи, моделировать условие с помощью схем, таблиц; составлять план решения, записывать решения с пояснениями, оценивать полученный ответ, проверяя ответ на соответствие условию;
моделировать в графической, предметной форме понятия и свойства, связанные с понятием обыкновенной дроби, читать и записывать дроби;
решать задачи на части (нахождение части от целого, целого по его известной части, какую часть составляет одна величина от другой);
складывать и вычитать дроби с равными знаменателями, умножать дроби на натуральные числа;
исследовать закономерности с обыкновенными дробями, проводить числовые эксперименты;
выполнять сложение и вычитание со смешанными числами; переводить неправильную дробь в смешанное число и обратно;
Формулировать, записывать с помощью букв основное свойство обыкновенной дроби, правила действия с обыкновенными дробями;
представлять обыкновенные дроби в виде десятичных и десятичные в виде обыкновенных;
строить на координатной прямой точки по заданным координатам, представленных в виде десятичных дробей; определять координаты точек;
сравнивать и упорядочивать десятичные дроби, выполнять вычисления с десятичными дробями;
исследовать закономерности с десятичными дробями;
складывать и вычитать десятичные дроби;
находить сумму разрядных слагаемых десятичных дробей;
читать и записывать десятичные периодические дроби;
находить десятичные приближения обыкновенных дробей, выполнять прикидку и оценку вычислений;
объяснять, что такое процент, представлять проценты в дробях и дроби в процентах, осуществлять поиск информации (в СМИ), содержащей данные, выраженные в процентах, интерпретировать их, решать задачи на проценты;
находить среднее арифметическое чисел;
выполнять практические работы по нахождению средней длины шага, среднего роста учеников класса, скорости чтения и др.;
округлять натуральные числа;
пользоваться римской системой счисления;
выполнять действия с натуральными числами, обыкновенными и десятичными дробями;
пользоваться справочными материалами, предметным указателем, списком дополнительной литературы, навигаторами и поисковыми системами Интернета.
1 Федеральный государственный образовательный стандарт основного общего образования / М-во образования и науки РФ. – М.: Просвещение, 2011. (Стандарты второго поколения). Приказ Министерства образования и науки РФ от 17.12.2010. №1897
2 Данилюк А.Я., Кондаков А.М., Тишков В.А. Концепция духовно-нравственного развития и воспитания личности гражданина России. – М.: Просвещение, 2010. (Стандарты второго поколения).
3 Примерные программы по учебным предметам. Математика. 5-9 классы: проект. – М.: Просвещение, 2010. (Стандарты второго поколения).
4 Примерные программы по учебным предметам. Математика. 5-9 классы. – М.: Просвещение, 2010. (Стандарты второго поколения).
26

 Получите свидетельство
Получите свидетельство Вход
Вход











 Рабочая программа по математике (5 класс ФГОС) (0.22 MB)
Рабочая программа по математике (5 класс ФГОС) (0.22 MB)
 2
2 2577
2577 487
487 Нравится
0
Нравится
0



