Муниципальное казенное общеобразовательное учреждение
| Рассмотрено Руководитель МО учителей математики _____ /В.И. Бойко / ФИО Протокол №___________ от «____»_________2015г. | Согласовано Заместитель директора по УВР _______ /И.А.Середина / ФИО
«____»_________2015г. | Утверждаю Директор
__________/Е.П.Богданова / ФИО Приказ № _______ от «____»_______2015г. |
«Богучарская средняя общеобразовательная школа № 1»
Рабочая программа
клуба «Математическая шкатулка»
на 2015-2016 учебный год
|
|
Класс 8а Учитель I КК В.И. Бойко
|
Содержание
Пояснительная записка стр. 3
Общая характеристика учебного предмета стр. 4
Описание места учебного предмета, курса в учебном плане стр. 5
Личностные, метапредметные и предметные результаты освоения
конкретного учебного предмета стр. 5
Содержание учебного предмета стр. 7
Тематическое планирование с определением основных видов
учебной деятельности стр. 8
Описание учебно-методического и материально-технического
обеспечения образовательного процесса стр. 9
Пояснительная записка
Данная программа разработана на основе:
Федерального государственного образовательного стандарта основного общего образования ( приказ Министерства образования и науки Российской Федерации от 17 декабря 2010 г. № 1897)
С учетом требований к оснащению образовательного процесса в соответствии с содержательным наполнением учебных предметов федерального компонента государственного стандарта общего образования;
Примерной основной образовательной программы образовательного учреждения. Основная школа / сост. Е. С. Савинов. – М.: Просвещение, 2011. – 454 с. – (Стандарты второго поколения).
Базисного учебного плана 2015 – 2016 учебного года.
Программа внеурочной деятельности предназначена для коррекции знаний учащихся 8 класса.
Данный курс направлен на коррекцию знаний учащихся за курс 7 и 8 классов, повышение уровня математической подготовки через решение линейных или квадратных уравнений, неравенств, расширение и углубление знаний.
Обоснование выбора программы, её актуальность
Программа данного курса является развитием системы ранее приобретенных программных знаний, его цель - создать целостное представление о теме и значительно расширить спектр задач, посильных для учащихся. Все свойства, входящие в данный курс, и их доказательства не вызовут трудности у учащихся, т.к. не содержат громоздких выкладок, а каждое предыдущее готовит последующее. При направляющей роли учителя школьники могут самостоятельно сформулировать новые для них свойства и даже доказать их. Программа данного курса располагает к самостоятельному поиску и повышать интерес к изучению предмета.
Цели обучения
1. В направлении личностного развития:
развитие логического и критического мышления, культуры речи, способности к умственному эксперименту;
формирование у учащихся интеллектуальной честности и объективности, способности к преодолению мыслительных стереотипов, вытекающих из обыденного опыта;
воспитание качеств личности, обеспечивающих социальную мобильность, способность принимать самостоятельные решения;
формирование качеств мышления, необходимых для адаптации в современном информационном обществе;
развитие интереса к математическому творчеству и математических способностей.
2. В метапредметном направлении:
развитие представлений о математике как форме описания и методе познания действительности, создание условий для приобретения первоначального опыта математического моделирования;
формирование общих способов интеллектуальной деятельности, характерных для математики и являющихся основой познавательной культуры, значимой для различных сфер человеческой деятельности.
3. В предметном направлении:
овладение математическими знаниями и умениями, необходимыми для продолжения обучения в старшей школе или иных общеобразовательных учреждениях, изучения смежных дисциплин, применения в повседневной жизни;
создание фундамента для математического развития, формирования механизмов мышления, характерных для математической деятельности.
Образовательные задачи программы.
Научить школьников выполнять тождественные преобразования выражений;
Научить учащихся решать линейные уравнения и неравенства;
Научить учащихся решать квадратные уравнения и неравенства;
Научить строить графики линейных и квадратных функций;
Помочь овладеть умениями на уровне свободного их использования;
Помочь ученики оценить свой потенциал с точки зрения образовательной перспективы.
Механизмы формирования ключевых компетенций учащихся
Программа предполагает, что успех формирования компетенций определяется рядом условий:
настроенностью уч-ся на необходимость определенных действий
четкостью и доступностью изложения цели и задач, которые уч-ся должны решать в ходе учебной деятельности
полнотой и ясностью представления о структуре формируемого умения, показом учителем способов выполнения той или иной работы
организацией деятельности учащихся по овладению отдельными действиями или их совокупностью с использованием системы задач
применение деятельностного подхода обучения
Общая характеристика курса
При обучении детей необходимо учитывать возрастные особенности.
Этому возрасту свойственно субъективное переживание, чувство взрослости: потребность равноправия, уважения и самостоятельности, требование серьезного, доверительного отношения со стороны взрослых. Пренебрежение этими требованиями, неудовлетворение этой потребности обостряет негативные черты кризисного периода.
К учебной деятельности подросток предъявляет новые требования: она должна обеспечить условия для его самооценки и самораскрытия, должна быть значимой для уважаемых подростком людей, для общества. Для подростков становится принципиальной их личная склонность к изучению того или иного предмета, знание цели изучения предмета, возможность применения результатов обучения в решении практических задач. Подростков не удовлетворяет роль пассивных слушателей, им неинтересно записывать готовые решения. Они ждут новых форм обучения, в которых были бы реализованы их активность, деятельный характер мышления, тяга к самостоятельности.
Ведущие виды деятельности подростков
Совместно-распределенная учебная деятельность в личностно-ориентированных формах (включающих возможность самостоятельного планирования и целеполагания, возможность проявить свою индивидуальность, выполнять «взрослые» функции – контроля, оценки, дидактической организации материала и пр.).
Совместно-распределенная проектная деятельность, ориентированная на получение социально-значимого продукта.
Исследовательская деятельность в ее разных формах, в том числе, осмысленное экспериментирование с природными объектами, социальное экспериментирование, направленное на выстраивание отношений с окружающими людьми, тактики собственного поведения.
Деятельность управления системными объектами (техническими объектами, группами людей).
Творческая деятельность (художественное, техническое и другое творчество), направленная на самореализацию и самоосознание.
Формы контроля: индивидуальное домашнее задание, консультация, игра, мини – олимпиада.
Условия реализации программы.
При реализации программы применяются элементы технологий:
Личностно-ориентированного обучения
Дифференцированного обучения
Проблемного обучения
Игровые технологии
Формы организации познавательной деятельности учащихся на уроке:
- индивидуально-обособленная
- фронтальная работа
- групповая работа
- коллективная работа
При реализации программы используются методы учебно-познавательной деятельности школьников: объяснительно-иллюстративный, репродуктивный, метод проблемного изложения (частично-поисковый), по источникам знаний (словесные, наглядные, практичные), по логике раскрытия учебного материала (индуктивные и дедуктивные) и по степени самостоятельности учащихся
Выделяются следующие виды системы уроков:
Урок-лекция. Предполагаются совместные усилия учителя и учеников для решения общей проблемной познавательной задачи. На таком уроке используется демонстрационный материал на компьютере, разработанный учителем или учениками, мультимедийные продукты.
Комбинированный урок предполагает выполнение работ и заданий разного вида. Урок–игра. На основе игровой деятельности учащиеся познают новое, закрепляют изученное, отрабатывают различные учебные навыки.
Урок решения задач. Вырабатываются у учащихся умения и навыки решения задач на уровне обязательной и возможной подготовки.
Урок-самостоятельная работа. Предлагаются разные виды самостоятельных работ
Место курса в учебном плане
Программа рассчитана на 70 часов в год, 1 час в неделю.
4. Результаты освоения курса
Программа обеспечивает достижения следующих результатов освоения образовательной программы основного общего образования:
личностные:
• формирование ответственного отношения к учению, готовности и способности обучающихся к саморазвитию и самообразованию на основе мотивации к обучению и познанию, выбору дальнейшего образования на базе ориентировки в мире профессий и профессиональных предпочтений, осознанному построению индивидуальной образовательной траектории с учетом устойчивых познавательных интересов;
• формирование целостного мировоззрения, соответствующего современному уровню развития науки и общественной практики;
• формирование коммуникативной компетентности и общении и сотрудничестве со сверстниками, старшими и младшими в образовательной, общественно полезной, учебно-исследовательской, творческой и других видах деятельности;
• умение ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи, выстраивать аргументацию, приводить примеры и контрпримеры;
• критичность мышления, умение распознавать логически некорректные высказывания, отличать гипотезу от факта;
• креативность мышления, инициативу, находчивость, активность при решении геометрических задач;
• умение контролировать процесс и результат учебной математической деятельности;
• способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений;
метапредметные:
регулятивные универсальные учебные действия:
• умение самостоятельно планировать альтернативные пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач;
• умение осуществлять контроль по результату и способу действия на уровне произвольного внимания и вносить необходимые коррективы;
• умение адекватно оценивать правильность или ошибочность выполнения учебной задачи, ее объективную трудность и собственные возможности ее решения;
• понимание сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом;
• умение самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем;
• умение планировать и осуществлять деятельность, направленную на решение задач исследовательского характера;
познавательные универсальные учебные действия:
• осознанное владение логическими действиями определения понятий, обобщения, установления аналогий, классификации на основе самостоятельного выбора оснований и критериев, установления родовидовых связей;
• умение устанавливать причинно-следственные связи, строить логическое рассуждение, умозаключение (индуктивное, дедуктивное и по аналогии) и выводы;
• умение создавать, применять и преобразовывать знаково-символические средства, модели и схемы для решения учебных и познавательных задач;
• формирование и развитие учебной и общепользовательской компетентности в области использования информационно-коммуникационных технологий (ИКТ-компетентности);
• формирование первоначальных представлений об идеях и о методах математики как универсальном языке науки и техники, средстве моделирования явлений и процессов;
• умение видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни;
• умение находить в различных источниках информацию, необходимую для решения математических проблем, и представлять ее в понятной форме; принимать решение в условиях неполной и избыточной, точной и вероятностной информации;
• умение понимать и использовать математические средства наглядности (рисунки, чертежи, схемы и др.) для иллюстрации, интерпретации, аргументации;
• умение выдвигать гипотезы при решении учебных задач и понимать необходимость их проверки;
• умение применять индуктивные и дедуктивные способы рассуждений, видеть различные стратегии решения задач;
коммуникативные универсальные учебные действия:
• умение организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками: определять цели, распределять функции и роли участников, общие способы работы;
• умение работать в группе: находить общее решение и разрешать конфликты на основе согласования позиций и учета интересов;
• слушать партнера;
• формулировать, аргументировать и отстаивать свое мнение;
предметные
В результате изучения курса ученик должен
знать/понимать:
как используются математические формулы, уравнения и неравенства; примеры их применения для решения математических и практических задач;
как математически определенные функции могут описывать реальные зависимости; приводить примеры такого описания;
уметь:
выполнять арифметические действия с рациональными числами, сравнивать рациональные и действительные числа; находить в несложных случаях значение степеней с целыми показателями и корней; находить значения числовых выражений;
решать текстовые задачи, включая задачи, связанные с отношением и с пропорциональность величин, дробями и процентами;
составлять буквенные выражения и формулы по условию задач; осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления, осуществлять подстановку одного выражения в другое; выражать из формул одну переменную через остальные;
выполнять основные действия со степенями с целыми показателями, с многочленами и с алгебраическими дробями; выполнять разложение многочленов на множители; выполнять тождественные преобразования рациональных выражений;
применять свойства арифметических квадратных корней для вычисления значений и преобразований числовых выражений, содержащих квадратные корни;
решать линейные, квадратные уравнения и рациональные уравнения, сводящиеся к ним, системы двух линейных уравнений и несложные нелинейные системы;
решать линейные и квадратные неравенства с одной переменной и их системы;
решать текстовые задачи алгебраическим методом, интерпретировать полученный результат, проводить отбор решений исходя из формулировки задачи;
изображать числа точками на координатной прямой;
определять координаты точки плоскости, строить точки с заданными координатами; изображать множество решений линейного неравенства;
находить значение функции, заданной формулой, таблицей, графиком, по ее аргументу; находить значение аргумента по значению функции, заданной графиком или таблицей;
определять свойства функции по графику; применять графические представления при решении уравнений, систем, неравенств;
5.Содержание курса
1. Вся программа 7 класса по учебнику Ю.Н. Макарычев.
Дроби и проценты. Сравнение дробей. Вычисления с рациональными числами. Степень с натуральным показателем. Задачи на проценты.
Прямая и обратная пропорциональность. Зависимость и формулы. Прямая пропорциональность. Обратная пропорциональность. Пропорции. Решение задач с помощью пропорции. Пропорциональное деление. Задачи на «сложные» пропорции.
Введение в алгебру. Буквенная запись свойств действий над числами. Преобразование буквенных выражений. Раскрытие скобок. Приведение подобных слагаемых.
Уравнения. Алгебраический способ решение задач. Корни уравнения. Решение уравнения. Решение задач с помощью уравнений. Некоторые неалгебраические способы решения уравнений.
Координаты и графики. Множества точек на координатной прямой. Расстояние между точками координатной прямой. Множества точек на координатной плоскости. Графики.
Свойства степени с натуральным показателем. Произведение и частное степеней. Степень степени. Произведения и дроби.
Многочлены. Одночлены и многочлены. Сложение и вычитание многочленов. Умножение одночлена на многочлен. Умножение многочлена на многочлен. Формулы квадрата суммы и квадрата разности. Решение задач с помощью уравнений.
Разложения многочленов на множители. Вынесение общего множителя за скобки. Способ группировки. Формула разности квадратов. Формула разности и суммы кубов. Разложение на множители с применением нескольких способов. Решение уравнений с помощью разложения на множители.
2. Вся программа 8 класса по учебнику Ю.Н. Макарычев.
Алгебраические дроби. Что такое алгебраическая дробь. Основное свойство дроби. Сложение и вычитание алгебраических дробей. Умножение и деление алгебраических дробей. Степень с целым показателем. Свойства степени с целым показателем. Решение уравнений и задач.
Квадратные корни. Задача о нахождении стороны квадрата. Иррациональные числа. Теорема Пифагора. Квадратный корень (алгебраический подход). Преобразование выражений, содержащих квадратные корни.
Кубический корень.
Квадратные уравнения. Какие уравнения называются квадратными. Формула корней квадратного уравнения. Теорема Виета. Разложение квадратного трехчлена на множители.
Системы уравнений. Линейное уравнение с двумя переменными и его график. Уравнение прямой вида y=kx+1. Системы уравнение. Решение систем способом сложения. Решение систем уравнений способом подстановки. Решение задач с помощью систем уравнений. Задачи на координатной плоскости.
Функции. Чтение графиков. Что такое функция. График функции. Свойства функции. Линейная функция. Функция 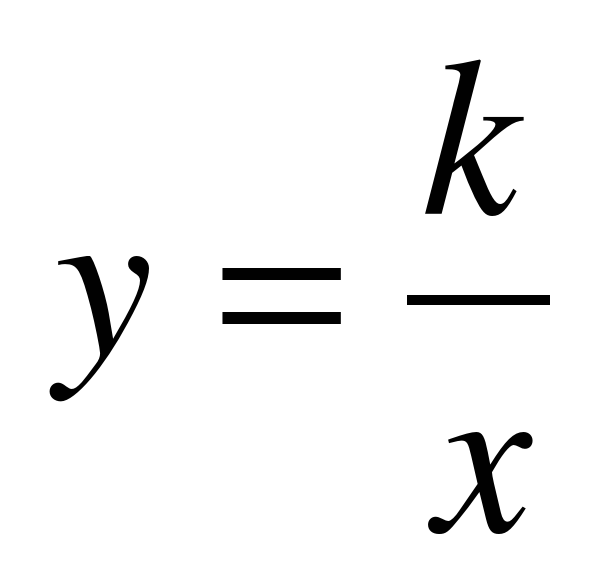 и её график.
и её график.
6. Тематическое планирование
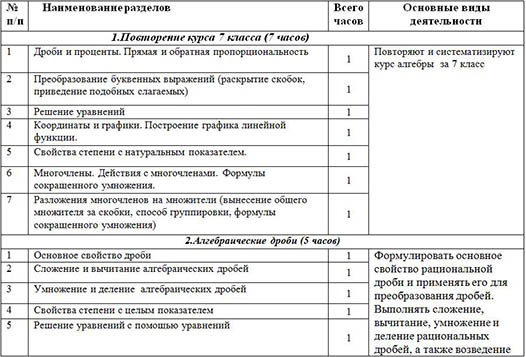
| № п/п | Наименование разделов | Всего часов | Основные виды деятельности |
| 1.Повторение курса 7 класса (7 часов) |
| 1 | Дроби и проценты. Прямая и обратная пропорциональность | 1 | Повторяют и систематизируют курс алгебры за 7 класс |
| 2 | Преобразование буквенных выражений (раскрытие скобок, приведение подобных слагаемых) | 1 |
| 3 | Решение уравнений | 1 |
| 4 | Координаты и графики. Построение графика линейной функции. | 1 |
| 5 | Свойства степени с натуральным показателем. | 1 |
| 6 | Многочлены. Действия с многочленами. Формулы сокращенного умножения. | 1 |
| 7 | Разложения многочленов на множители (вынесение общего множителя за скобки, способ группировки, формулы сокращенного умножения) | 1 |
| 2.Алгебраические дроби (5 часов) |
| 1 | Основное свойство дроби | 1 | Формулировать основное свойство рациональной дроби и применять его для преобразования дробей. Выполнять сложение, вычитание, умножение и деление рациональных дробей, а также возведение дроби в степень. Выполнять различные преобразования рациональных выражений, доказывать тождества.
|
| 2 | Сложение и вычитание алгебраических дробей | 1 |
| 3 | Умножение и деление алгебраических дробей | 1 |
| 4 | Свойства степени с целым показателем | 1 |
| 5 | Решение уравнений с помощью уравнений | 1 |
| 3. Квадратные корни (6 часов) |
| 1 | Нахождение стороны квадрата | 1 | Приводить примеры рациональных и иррациональных чисел. Находить значения арифметических квадратных корней, используя при необходимости калькулятор. Доказывать теоремы о корне из произведения и дроби, |
| 2 | Иррациональные числа | 1 |
| 3 | Теорема Пифагора | 1 |
| 4 | Квадратный корень (алгебраический подход) | 1 |
| 5 | Преобразование выражений, содержащих квадратные корни | 1 |
| 6 | Кубический корень | 1 |
| 4. Квадратные уравнения (5 часов) |
| 1 | Формулы корней квадратного уравнения | 1 | Решать квадратные уравнения. Находить побором корни квадратного уравнения, используя теорему Виета. Исследовать квадратные уравнения по дискриминанту и коэффициентам. |
| 2 | Неполные квадратные уравнения | 1 |
| 3 | Теорема Виета | 1 |
| 4 | Разложение квадратного трехчлена на множители | 2 |
| 5. Системы уравнений (6 часов) |
| 1 | Линейное уравнение с двумя переменными и его график | 1 | Применять способ подстановки и способ сложения при решении систем линейных уравнений с двумя переменными. Решать текстовые задачи, используя в качестве алгебраической модели систему уравнений. Интерпретировать результат, полученный при решении системы |
| 2 | Уравнение прямой вида y=kx+1 | 1 |
| 3 | Системы уравнений. Решение систем способом сложения | 1 |
| 4 | Системы уравнений. Решение систем способом подстановки | 1 |
| 5 | Решение задач с помощью систем уравнений | 1 |
| 6 | Задачи на координатной плоскости | 1 |
| 6. Функции (6 часов) |
| 1 | График функции, Свойства функций | 2 | Вычислять значения функции, заданной формулой, составлять таблицы значений функции. По графику функции находить значение функции по известному значению аргумента и решать обратную задачу.
|
| 2 | Линейная функция | 2 |
| 3 | Функция 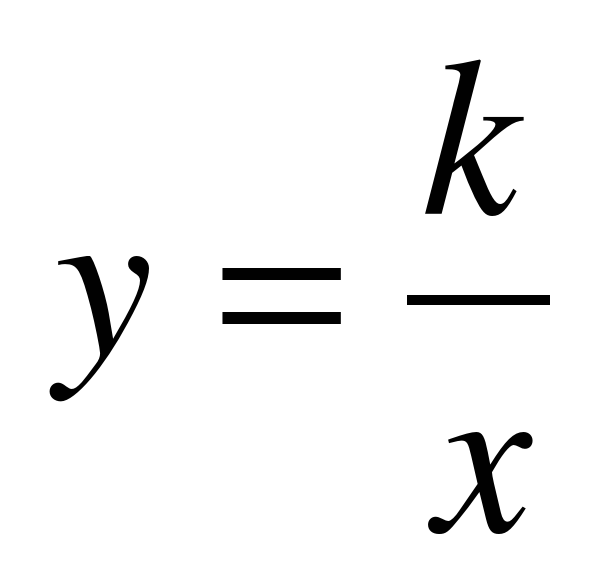 и её график и её график | 2 |
| Всего 35 |
7. Методическое обеспечение
1. Алгебра: учебник для 7 класса общеобразовательных учреждений. Под ред. Ю.Н. Макарычева. М.: Просвещение, 2010.
2. Математика: алгебра. Функции, анализ данных: учебник для 8 класса общеобразовательных учреждений. Под ред. Ю.Н. Макарычева. М.: Просвещение, 2010.
3. Алгебра 8. Тематические тесты. ГИА. Л.В. Кузнецова, С.С. Минаева
Календарно-тематическое планирование занятий клуба «Математическая шкатулка»
| № п/п | Дата | Факт. дата | Наименование разделов |
| 1 | 01.09 |
| Дроби и проценты. Прямая и обратная пропорциональность |
| 2 | 08.09 |
| Преобразование буквенных выражений (раскрытие скобок, приведение подобных слагаемых) |
| 3 | 15.09 |
| Решение уравнений |
| 4 | 22.09 |
| Координаты и графики. Построение графика линейной функции. |
| 5 | 29.09 |
| Свойства степени с натуральным показателем. |
| 6 | 06.10 |
| Многочлены. Действия с многочленами. Формулы сокращенного умножения. |
| 7 | 13.10 |
| Разложения многочленов на множители (вынесение общего множителя за скобки, способ группировки, формулы сокращенного умножения) |
| 8 | 20.10 |
| Основное свойство дроби |
| 9 | 27.10 |
| Сложение и вычитание алгебраических дробей |
| 10 | 10.11 |
| Умножение и деление алгебраических дробей |
| 11 | 17.11 |
| Свойства степени с целым показателем |
| 12 | 24.11 |
| Решение уравнений с помощью уравнений |
| 13 | 01.12 |
| Нахождение стороны квадрата |
| 14 | 08.12 |
| Иррациональные числа |
| 15 | 15.12 |
| Теорема Пифагора |
| 16 | 22.12 |
| Квадратный корень (алгебраический подход) |
| 17 | 29.12 |
| Преобразование выражений, содержащих квадратные корни |
| 18 | 12.01 |
| Кубический корень |
| 19 | 19.01 |
| Формулы корней квадратного уравнения |
| 20 | 26.01 |
| Неполные квадратные уравнения |
| 21 | 02.02 |
| Теорема Виета |
| 22 | 09.02 |
| Разложение квадратного трехчлена на множители |
| 23 | 16.02 |
| Разложение квадратного трехчлена на множители |
| 24 | 24.02 |
| Линейное уравнение с двумя переменными и его график |
| 25 | 01.03 |
| Уравнение прямой вида y=kx+1 |
| 26 | 15.03 |
| Системы уравнений. Решение систем способом сложения |
| 27 | 05.03 |
| Системы уравнений. Решение систем способом подстановки |
| 28 | 12.03 |
| Решение задач с помощью систем уравнений |
| 29 | 19.03 |
| Задачи на координатной плоскости |
| 30 | 26.03 |
| График функции, Свойства функций |
| 31 | 03.05 |
| График функции, Свойства функций |
| 32 | 10.05 |
| Линейная функция |
| 33 | 17.05 |
| Линейная функция |
| 34 | 24.05 |
| Функция 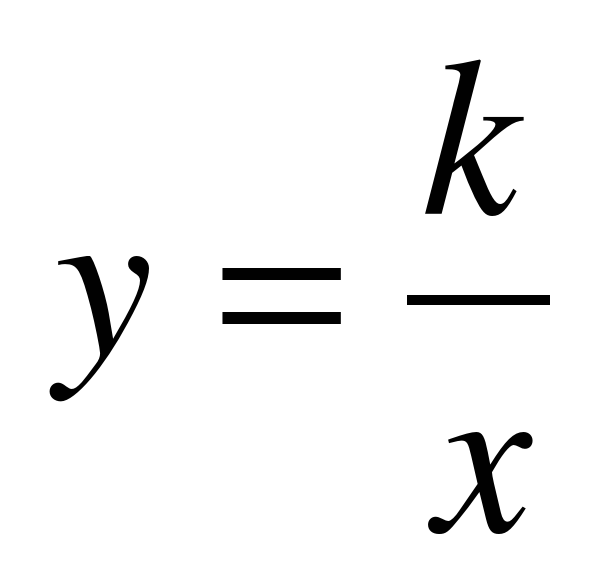 и её график и её график |
| 35 | 31.05 |
| Функция 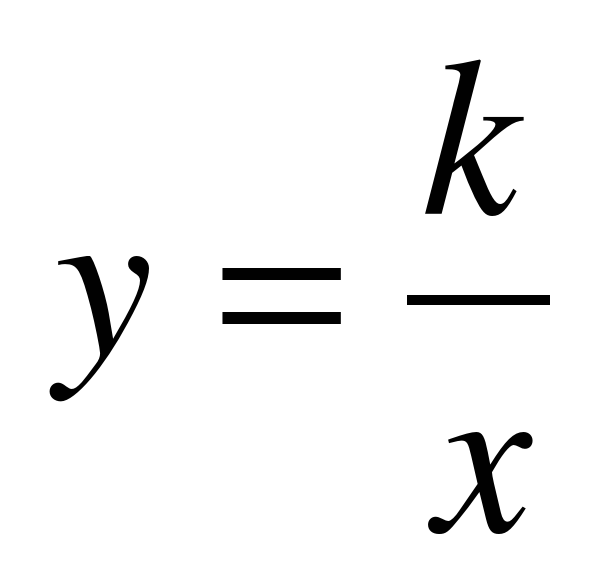 и её график и её график |
11

 Получите свидетельство
Получите свидетельство Вход
Вход











 Рабочая программа клуба «Математическая шкатулка» (8 класс) (0.15 MB)
Рабочая программа клуба «Математическая шкатулка» (8 класс) (0.15 MB)
 0
0 1005
1005 86
86 Нравится
0
Нравится
0








