РАБОЧАЯ ПРОГРАММА
по предмету «Алгебра»(ФКГОС)
для 7-9 классов
Пояснительная записка
Рабочая программа по алгебре разработана в соответствии с программой для
общеобразовательных учреждений – Алгебра. 7-9 классы. М.: «Просвещение», 2008г., с
учетом требований федерального компонента государственного образовательного стандарта
основного общего образования по математике, и основана на авторской программе линии
Ш.А. Алимова.
Календарно – тематический план ориентирован на использование учебников: Алгебра:
учебник для 7 класса общеобразовательных учреждений/ [Ш.А. Алимов, Ю.М. Колягин, Ю.В.
Сидоров и др.]. - М.: Просвещение, 2013.; Алгебра: учебник для 8 класса
общеобразовательных учреждений/ [Ш.А. Алимов, Ю.М. Колягин, Ю.В. Сидоров и др.]. - М.:
Просвещение, 2013.; Алгебра: учебник для 9 класса общеобразовательных учреждений/ [Ш.А.
Алимов, Ю.М. Колягин, Ю.В. Сидоров и др.]. - М.: Просвещение, 2013.
Алгебра нацелена на формирование математического аппарата для решения задач из
математики, смежных предметов, окружающей реальности. Язык алгебры подчеркивает
значение математики как языка для построения математических моделей, процессов и
явлений реального мира. Одной из основных задач изучения алгебры является развитие
алгоритмического мышления, необходимого, в частности, для освоения курса информатики;
овладение навыками дедуктивных рассуждений. Преобразование символических форм вносит
свой специфический вклад в развитие воображения, способностей к математическому
творчеству. Другой важной задачей изучения алгебры является получение школьниками
конкретных знаний о функциях как важнейшей математической модели для описания и
исследования разнообразных процессов (равномерных, равноускоренных, экспоненциальных,
периодических и др.), для формирования у учащихся представлений о роли математики в
развитии цивилизации и культуры.
В ходе освоения курса учащиеся получают возможность:
-развить представление о числе и роли вычислений в человеческой практике;
сформировать практические навыки выполнения устных, письменных, интеллектуальных
вычислений, развить вычислительную культуру;
-овладеть символическим языком алгебры, выработать формально-оперативные
алгебраические умения и научиться применять их к решению математических и
нематематических задач;
-изучить свойства и графики элементарных функций, научиться использовать
функционально-графические представления для описания и анализа реальных зависимостей;
-развить логическое мышление и речь – умение логически обосновывать суждения,
проводить несложные систематизации, приводить примеры и контрпримеры, использовать
различные языки математики (словесный, символический, графический) для иллюстрации,
интерпретации, аргументации и доказательства;
-сформировать представления об изучаемых понятиях и методах как важнейших
средствах математического моделирования реальных процессов и явлений.
Цели:
- овладение системой математических знаний и умений, необходимых для применения в
практической деятельности, изучения смежных дисциплин, продолжения образования;
- интеллектуальное развитие, формирование качеств личности, необходимых человеку для
полноценной жизни в современном обществе, свойственных математической деятельности:
ясности и точности мысли, критичности мышления, интуиции, логического мышления,
элементов алгоритмической культуры, пространственных представлений, способности к
преодолению трудностей;
- формирование представлений об идеях и методах математики как универсального языка
науки и техники, средства моделирования явлений и процессов;
- воспитание культуры личности, отношения к математике как к части общечеловеческой
культуры, играющей особую роль в общественном развитии.
Задачи:
При изучении курса математики на базовом уровне продолжаются и получают развитие
содержательные линии: «Числа и вычисления», «Выражения и их преобразования»,
«Функции», «Уравнения и неравенства», «Геометрия», «Элементы комбинаторики, теории
вероятностей, статистики и логики». В рамках указанных содержательных линий решаются
следующие задачи:
- развитие представление о числе и роли вычислений в человеческой практике; формирование
практических навыков выполнения устных, письменных, инструментальных вычислений,
развитие вычислительной культуры;
- овладение символическим языком алгебры, выработка формально-оперативные
алгебраических умений и применение их к решению математических и нематематических
задач;
- изучение свойств и графиков элементарных функций, научиться использовать
функционально-графические представления для описания и анализа реальных зависимостей;
- развитие пространственных представлений и изобразительных умений, освоение основных
фактов и методов планиметрии, знакомство с простейшими пространственными телами и их
свойствами;
- получение представления о статистических закономерностях в реальном мире и о различных
способах их изучения, об особенностях выводов и прогнозов, носящих вероятностный
характер;
- развитие логического мышления и речи – умения логически обосновывать суждения,
проводить несложные систематизации, приводить примеры и контрпримеры, использовать
различные языки математики (словесный, символический, графический) для иллюстрации,
интерпретации, аргументации и доказательства;
- формирование представления об изучаемых понятиях и методах как важнейших средствах
математического моделирования реальных процессов и явлений.
Место учебного предмета в учебном плане
Согласно федеральному базисному учебному плану для образовательных учреждений
Российской Федерации на изучение алгебры на ступени основного общего образования
отводится не менее 306 часов из расчета 3 часа в неделю (всего 102ч) с 7 по 9 класс.
Преобладающей формой текущего контроля выступает письменный (самостоятельные и
контрольные работы) и устный опрос (собеседование).
2. Содержание учебного предмета
Алгебраические выражения. Буквенные выражения (выражения с переменными).
Числовое значение буквенного выражения. Допустимые значения переменных, входящих в
алгебраические выражения. Подстановка выражений вместо переменных. Равенство
буквенных выражений.
Тождество, доказательство тождеств. Преобразования выражений. Свойства степеней с
целым показателем. Многочлены. Сложение, вычитание, умножение многочленов. Формулы
сокращенного умножения: квадрат суммы и квадрат разности, куб суммы и куб разности.
Формула разности квадратов, формула суммы кубов и разности кубов. Разложение
многочлена на множители. Квадратный трехчлен. Выделение полного квадрата в квадратном
трехчлене. Теорема Виета. Разложение квадратного трехчлена на линейные множители.
Многочлены с одной переменной. Степень многочлена. Корень многочлена.
Алгебраическая дробь. Сокращение дробей. Действия с алгебраическими дробями.
Рациональные выражения и их преобразования. Свойства квадратных корней и их
применение в вычислениях.
Уравнения и неравенства. Уравнение с одной переменной. Корень уравнения. Линейное
уравнение. Квадратное уравнение: формула корней квадратного уравнения, Решение
рациональных уравнений. Примеры решения уравнений высших степеней; методы замены
переменной, разложения на множители.
Уравнение с двумя переменными; решение уравнения с двумя переменными. Система
уравнений; решение системы. Система двух линейных уравнений с двумя переменными;
решение подстановкой и алгебраическим сложением. Уравнение с несколькими
переменными. Примеры решения нелинейных систем. Примеры решения уравнений в целых
числах.
Неравенство с одной переменной. Решение неравенства. Линейные неравенства с одной
переменной и их системы. Квадратные неравенства. Примеры решения дробно-линейных
неравенств.
Числовые неравенства и их свойства. Доказательство числовых и алгебраических
неравенств. Переход от словесной формулировки соотношений между величинами к
алгебраической. Решение текстовых задач алгебраическим способом.
Числовые последовательности. Понятие последовательности. Арифметическая и
геометрическая прогрессии. Формулы общего члена арифметической и геометрической
прогрессий, суммы первых нескольких членов арифметической и геометрической
прогрессий. Cложные проценты.
Числовые функции. Понятие функции. Область определения функции. Способы задания
функции. График функции, возрастание и убывание функции, наибольшее и наименьшее
значения функции, нули функции, промежутки знакопостоянства. Чтение графиков функций.
Функции, описывающие прямую и обратную пропорциональную зависимости, их графики.
Линейная функция, ее график, геометрический смысл коэффициентов. Гипербола.
Квадратичная функция, ее график, парабола. Координаты вершины параболы, ось
симметрии. Степенные функции с натуральным показателем, их графики. Графики функций:
корень квадратный, корень кубический, модуль.
Использование графиков функций для решения уравнений и систем. Примеры графических
зависимостей, отражающих реальные процессы: колебание, показательный рост; числовые
функции, описывающие эти процессы.
Параллельный перенос графиков вдоль осей координат и симметрия относительно
осей.
Координаты. Изображение чисел точками координатной прямой. Геометрический смысл
модуля числа. Числовые промежутки: интервал, отрезок, луч. Формула расстояния между
точками координатной прямой.
Декартовы координаты на плоскости; координаты точки. Координаты середины отрезка.
Формула расстояния между двумя точками плоскости. Уравнение прямой, угловой
коэффициент прямой, условие параллельности прямых. Уравнение окружности с центром
в начале координат и в любой заданной точке.
Графическая интерпретация уравнений с двумя переменными и их систем, неравенств с
двумя переменными и их систем
Элементы логики, комбинаторики, статистики и теории вероятностей
Доказательство. Определения, доказательства, аксиомы и теоремы; следствия.
Необходимые
и достаточные условия. Контр пример. Доказательство от противного. Прямая и обратная
теоремы.
Понятие об аксиоматике и аксиоматическом построении геометрии. Пятый постулат
Эвклида и его история.
Множества и комбинаторика. Множество. Элемент множества, подмножество.
Объединение и пересечение множеств. Диаграммы Эйлера. Примеры решения
комбинаторных задач: перебор вариантов, правило умножения.
Статистические данные. Представление данных в виде таблиц, диаграмм, графиков.
Средние результатов измерений. Понятие о статистическом выводе на основе выборки.
Понятие и примеры случайных событий.
Вероятность. Частота события, вероятность. Равновозможные события и подсчет их
вероятности. Представление о геометрической вероятности.
Содержание тем учебного курса 7 класса
Алгебраические выражения. (10часов).
Числовые и буквенные выражения. Числовое значение буквенного выражения.
Буквенные выражения (выражения с переменными). Числовое значение буквенного
выражения. Допустимые значения переменных, входящих в алгебраические выражения.
Подстановка выражений вместо переменных. Равенство буквенных выражений.
Преобразования выражений
Основная цель – сформировать умение осуществлять в буквенных выражениях
числовые подстановки и выполнять соответствующие вычисления; сравнивать значения
буквенных выражений при заданных значениях входящих в них переменных; применять
свойства действий над числами при нахождении значений числовых выражений.
Уравнения с одним неизвестным (8 часов,).
Уравнения первой степени с одним неизвестным. Линейные уравнения с одним
неизвестным. Решение линейных уравнений с одним неизвестным. Решение задач с
помощью линейных уравнений.
Основная цель – сформировать умения решать линейные уравнения, задачи,
сводящиеся к линейным уравнениям.
Одночлены и многочлены (17часов).
Степень с натуральным показателем и её свойства. Стандартный вид числа.
Преобразование рациональных выражений, записанных с помощью степени с натуральным
показателем.
Числовые и буквенные выражения. Числовое значение буквенного выражения.
Одночлен, произведение одночленов, подобные одночлены. Многочлен, сумма и разность
многочленов, произведение одночлена на многочлен, произведение многочленов. Степень
многочлена. Целое выражение и его числовое значение. Тождественное равенство целых
выражений.
Основная цель – сформировать умения выполнять преобразования с одночленами и
многочленами , сформировать умение выполнять арифметические действия с числами,
записанными в стандартном виде, и преобразовывать рациональные выражения, записанные
с помощью степени с натуральным показателем.
Разложение многочленов на множители (17 часов). Вынесение общего
множителя за скобки. Способ группировки. Формула разности квадратов. Квадрат суммы
и разности. Куб суммы и куб разности, Формула суммы кубов и разности кубов.
Применение формул сокращенного умножения. Разложение многочлена на множители.
Основная цель – сформировать умения, связанные с применением формул
сокращенного умножения для преобразования квадрата суммы и разности в многочлен, для
разложения многочлена на множители.
Алгебраические дроби (20 часов).
Алгебраические дроби и их свойства, сокращение дробей. Арифметические действия
над алгебраическими дробями. Рациональные выражения, их преобразования и числовое
значение. Допустимые значения переменных, входящих в алгебраические выражения.
Тождественное равенство рациональных выражений.
Основная цель – сформировать умения применять основное свойство дроби и
выполнять над алгебраическими дробями арифметические действия.
Линейная функция и ее график ( 10 часов)
Декартовы координаты на плоскости; координаты точки.
Понятие функция. Функция y=kx и ее график. Линейная функция и ее график.
Основная цель – дать понятие функции, области определения функции, области
значений, что такое аргумент, какая переменная называется зависимой, какая независимой,
сформировать умение находить значения функций, заданных формулой, таблицей,
графиком; решать обратную задачу; строить графики линейной функции, прямой
пропорциональности;
Системы двух уравнений с двумя неизвестными (11 часов).
Уравнения первой степени с двумя неизвестными. Система уравнений, решения
системы. Система двух линейных уравнений с двумя переменными, решение систем двух
линейных уравнений с двумя неизвестными подстановкой и алгебраическим сложением.
Графический способ решения систем уравнений. Решение задач с помощью
систем уравнений.
Основная цель – сформировать умения решать системы двух линейных уравнений и
задачи, сводящиеся к системе линейных уравнений.
Введение в комбинаторику ( 7 часов)
Исторические комбинаторные задачи. Различные комбинации из трёх элементов.
Таблица вариантов и правило произведения. Подсчёт вариантов с помощью графов.
Перестановки
Разбиения на группы. Выдвижение гипотез.
Основная цель – познакомить элементами комбинаторики: различные комбинации из
трёх элементов, таблица вариантов и правило произведения, подсчёт вариантов с помощью
графов.
Повторение (2 часа).
Содержание тем учебного курса 8 класса
Неравенства (19ч)
Положительные и отрицательные числа. Числовые неравенства, их свойства.
Сложение и умножение неравенств. Строгие и нестрогие неравенства. Неравенства с одним
неизвестным. Система неравенств с одним неизвестным.
Приближенные вычисления (14)
Приближенные значения величин. Погрешность приближения. Оценка погрешности.
Округление чисел. Относительная погрешность. Простейшие вычисления на калькуляторе.
Стандартный вид числа. Вычисления на калькуляторе степени числа и числа. Обратного
данному. Последовательность выполнения нескольких операций на калькуляторе.
Вычисления на калькуляторе с использованием ячеек памяти.
Квадратные корни (14)
Понятие арифметического квадратного корня. Действительные числа. Квадратный
корень из степени, произведения и дроби.
Квадратные уравнения (23)
Квадратное уравнения и его корни. Неполные квадратные уравнения. Метод
выделения полного квадрата. Решение квадратных уравнений. Приведенное квадратное
уравнение. Теорема Виета. Уравнения, сводящиеся к квадратным. Решение задач с помощью
квадратных уравнений. Решение простейших систем, содержащих уравнение второй
степени.
Квадратичная функция (16)
Определение квадратичной функции. Функции у=х2, у=ах2, у=ax2+bx+c. Построение
графика
Квадратные неравенства (12ч)
Квадратное неравенство и его решение. Решение квадратного неравенства с помощью
графика квадратичной функции.
Повторение (4ч)
Содержание тем учебного курса 9 класса
1.Вводное повторение – 4 часа.
Квадратные уравнения, замена переменной, биквадратное уравнение. Неравенства
второй степени с одной переменной, нули функции, метод интервалов, график
квадратичной функции.
Уметь выполнять упражнения из разделов курса VIII класса: решать квадратные
уравнения и неравенства, задачи с помощью квадратных уравнений, строить график
квадратичной функции.
Знать формулы решения квадратных уравнений, алгоритм построения параболы,
теорему Виета.
2. Алгебраические уравнения. Системы нелинейных уравнений – 15 часов.
Знать: алгоритм решения алгебраических уравнений и уравнений, сводящихся к ним.
Уметь: решать алгебраические уравнения и системы уравнений, выполнять деление
многочленов, решать задачи с помощью уравнений. Основные термины по разделу:
многочлен, алгоритм деления многочленов, формула деления многочленов,
уравнения третьей и четвёртой степеней, понятие возвратного уравнения, системы
нелинейных уравнений.
3. Степень с рациональным показателем – 10 часов.
Знать: степень с целым и рациональным показателями и их свойства; степень с
нулевым и отрицательным показателями; определение арифметического корня
натуральной степени и его свойства.
Уметь: находить значение степени с целым показателем при конкретных значениях
основания и показателя степени и применять свойства степени для вычисления
значений числовых выражений и выполнения простейших преобразований.
Основные термины по разделу:
определение степени с целым отрицательным и рациональным показателем;
нулевым показателем, определение и свойства арифметического корня n-й степени.
4. Степенная функция – 17 часов.
Знать: понятия область определения, чётность и нечётность функции, возрастание и
убывание функции на промежутке.
Уметь: строить графики линейных и дробно-линейных функций и по графику
перечислять их свойства; решать уравнения и неравенства, содержащие степень.
Основные термины по разделу:
функция, область определения и область изменения, нули функции, возрастающая и
убывающая функция, четные и нечетные функции, их симметричность, понятие
функции у=k/х, обратно пропорциональная зависимость, свойства степенной функции,
иррациональное уравнение.
5. Прогрессии – 14 часов.
Знать: определения арифметической и геометрической прогрессий, формулы суммы n
первых членов арифметической и геометрической прогрессий; определение
бесконечно убывающей геометрической прогрессии.
Уметь: решать задачи на нахождение неизвестного члена арифметической и
геометрической прогрессии, проверять является ли данное число членом прогрессии,
находить сумму n первых членов прогрессии.
Основные термины по разделу:
арифметическая и геометрическая прогрессии, формула n-го члена прогрессии,
формула суммы n-членов прогрессии и нескольких первых членов прогрессий.
6. Случайные события – 11 часов.
Уметь: ориентироваться в комбинаторике; строить дерево возможных вариантов
Знать и уметь пользоваться формулами для решения комбинаторных задач
Основные термины по разделу. Перебор возможных вариантов, комбинаторное правило
умножения, перестановки, число всевозможных перестановок, размещения, сочетания.
7. Случайные величины – 12 часов.
Уметь: определять количество равновозможных исходов некоторого испытания;
Знать классическое определение вероятности, формулу вычисления вероятности в
случае исхода противоположных событий
Основные термины по разделу:
Случайное событие, относительная частота, классическое определение вероятности,
противоположные события, независимые события, несовместные и совместные
события.
8. Множества. Логика – 11 часов.
Уметь: решать задачи, применяя теоремы множеств, круги Эйлера, с использованием
логических связок «и», «или», «не».
Знать понятия множества, подмножества, пересечение множеств, объединение множеств;
понятие высказывания.
Основные термины по разделу:
множество, подмножество, высказывание, логическая связка.
9. Итоговое повторение - 8часов.
-знать алгоритм построения графика функции; формулы n-го члена и суммы n членов
арифметической и геометрической прогрессий и уметь их применять при решении
задач
-уметь строить графики функции; по графику определять свойства функции
-уметь решать уравнения третьей и четвертой степени с одним неизвестным с
помощью разложения на множители и введения вспомогательной переменной;
решать неравенства методом интервалов; решать системы уравнений; решать задачи
с помощью составления систем.
3. Требования к уровню подготовки учащихся
Требования к уровню подготовки учащихся 7 класса:
должны знать/понимать:
- математический язык;
- свойства степени с натуральным показателем;
- определение одночлена и многочлена, операции над одночленами и многочленами;
формулы сокращенного умножения; способы разложения на множители;
- линейную функцию, ее свойства и график;
- способы решения систем двух линейных уравнений с двумя переменными;
должны уметь:
- составлять математическую модель при решении задач;
- выполнять действия над степенями с натуральными показателями, используя
свойства степеней;
- выполнять арифметические операции над одночленами и многочленами,
раскладывать многочлены на множители, используя метод вынесения общего множителя
за скобки, метод группировки, формулы сокращенного умножения;
- строить график линейной функции;
- решать системы двух линейных уравнений с двумя переменными;
способны решать следующие жизненно-практические задачи:
- самостоятельно приобретать и применять знания в различных ситуациях;
- работать в группах, аргументировать и отстаивать свою точку зрения, уметь
слушать других;
- извлекать учебную информацию на основе сопоставительного анализа объектов;
- пользоваться предметным указателем, энциклопедией и справочником для
нахождения информации;
- самостоятельно действовать в ситуации неопределенности при решении
актуальных для них проблем.
Требования к уровню подготовки учащихся 8 класса
В результате изучения курса алгебры в 8 классе учащиеся должны
знать/понимать:
- значение математической науки для решения задач, возникающих в теории и
практике; широту и в то же время ограниченность применения математических методов
к анализу и исследованию процессов и явлений в природе и обществе;
-значение практики и вопросов, возникающих в самой математике, для
формирования и развития математической науки; историю развития понятия числа;
- универсальный характер законов логики математических рассуждений, их
применения во всех областях человеческой деятельности;
уметь:
- выполнять арифметические действия, сочетая устные и письменные приемы;
находить значения корня натуральной степени, используя при необходимости
вычислительные устройства; пользоваться оценкой и прикидкой при практических
расчетах;
- составлять буквенные выражения и формулы по условиям задач; осуществлять в
выражениях и формулах числовые подстановки и выполнять соответствующие
вычисления, осуществлять подстановку одного выражения в другое; выражать из
формул одну переменную через остальные;
- выполнять основные действия со степенями с целыми показателями, с
многочленами и с алгебраическими дробями; выполнять разложение многочленов на
множители; выполнять тождественные преобразования рациональных выражений;
- применять свойства арифметических квадратных корней для вычисления
значений и преобразований числовых выражений, содержащих квадратные корни;
- решать линейные, квадратные уравнения и рациональные уравнения,
сводящиеся к ним, системы двух линейных уравнений и несложные нелинейные
системы;
- решать линейные и квадратные неравенства с одной переменной и их системы,
- решать текстовые задачи алгебраическим методом, интерпретировать
полученный результат, проводить отбор решений, исходя из формулировки задачи;
- изображать числа точками на координатной прямой;
- определять координаты точки плоскости, строить точки с заданными
координатами; изображать множество решений линейного неравенства;
- находить значения функции, заданной формулой, таблицей, графиком по ее
аргументу; находить значение аргумента по значению функции, заданной графиком или
таблицей;
- определять свойства функции по ее графику; применять графические
представления при решении уравнений, систем, неравенств;
- описывать свойства изученных функций, строить их графики;
- извлекать информацию, представленную в таблицах, на диаграммах, графиках;
составлять таблицы, строить диаграммы и графики;
владеть компетенциями:
познавательной, коммуникативной, информационной и рефлексивной;
решать следующие жизненно-практические задачи:
- самостоятельно приобретать и применять знания в различных ситуациях,
работать в группах;
- аргументировать и отстаивать свою точку зрения;
-уметь слушать других, извлекать учебную информацию на основе
сопоставительного анализа объектов;
- пользоваться предметным указателем энциклопедий и справочников для
нахождения информации;
- самостоятельно действовать в ситуации неопределенности при решении
актуальных для них проблем.
использовать приобретенные знания и умения в практической деятельности
и повседневной жизни для:
-выполнения расчетов по формулам, для составления формул, выражающих
зависимости между реальными величинами; для нахождения нужной формулы в
справочных материалах;
- моделирования практических ситуаций и исследовании построенных моделей с
использованием аппарата алгебры;
- описания зависимостей между физическими величинами соответствующими
формулами, при исследовании несложных практических ситуаций;
- интерпретации графиков реальных зависимостей между величинами.
Требования к уровню подготовки учащихся 9 класса
В результате изучения курса алгебры 9 класса учащиеся должны:
уметь:
- уметь решать уравнения, системы уравнений более высоких степеней.
- находить по графику промежутки возрастания и убывания функции, а также
промежутки, в которых функция сохраняет знак;
- понимать содержательный смысл важнейших свойств функции; по графику
функции отвечать на вопросы, касающиеся её свойств;
- бегло и уверенно выполнять арифметические действия с рациональными числами;
вычислять значения числовых выражений, содержащих степени и корни;
- решать простейшие системы, содержащие уравнения второй степени с двумя
переменными; решать текстовые задачи с помощью составления таких систем;
- решать квадратные уравнения и уравнения, сводящиеся к ним, используя приемы и
формулы для решения различных видов квадратных уравнений, графический способ
решения уравнений;
- распознавать арифметические и геометрические прогрессии; решать задачи с
применением формулы общего члена и суммы нескольких первых членов;
- использовать приобретенные знания, умения, навыки в практической деятельности
и повседневной жизни для:
- решения несложных практических расчетных задач, в том числе с
использованием при необходимости справочной литературы, калькулятора, компьютера;
- устной прикидки, и оценки результата вычислений, проверки результата
вычислений выполнением обратных действий;
- интерпретации результата решения задач.
знать/понимать
- существо понятия математического доказательства; примеры доказательств;
- существо понятия алгоритма; примеры алгоритмов;
- как используются математические формулы, уравнения и неравенства; примеры их
применения для решения математических и практических задач;
- как математически определенные функции могут описывать реальные зависимости;
приводить примеры такого описания;
- как потребности практики привели математическую науку к необходимости расширения
понятия числа;
- вероятностный характер многих закономерностей окружающего мира; примеры
статистических закономерностей и выводов;
- каким образом геометрия возникла из практических задач землемерия; примеры
геометрических объектов и утверждений о них, важных для практики;
- смысл идеализации, позволяющей решать задачи реальной действительности
математическими методами, примеры ошибок, возникающих при идеализации;
Алгебра
уметь
- составлять буквенные выражения и формулы по условиям задач; осуществлять
в выражениях и формулах числовые подстановки и выполнять соответствующие
вычисления, осуществлять подстановку одного выражения в другое; выражать из
формул одну переменную через остальные;
- выполнять основные действия со степенями с целыми показателями, с
многочленами и с алгебраическими дробями; выполнять разложение многочленов на
множители; выполнять тождественные преобразования рациональных выражений;
- применять свойства арифметических квадратных корней для вычисления
значений и преобразований числовых выражений, содержащих квадратные корни;
- решать линейные, квадратные уравнения и рациональные уравнения,
сводящиеся к ним, системы двух линейных уравнений и несложные нелинейные
системы;
- решать линейные и квадратные неравенства с одной переменной и их системы;
- решать текстовые задачи алгебраическим методом, интерпретировать
полученный результат, проводить отбор решений, исходя из формулировки задачи;
- изображать числа точками на координатной прямой;
- определять координаты точки плоскости, строить точки с заданными
координатами; изображать множество решений линейного неравенства;
- распознавать арифметические и геометрические прогрессии; решать задачи с
применением формулы общего члена и суммы нескольких первых членов;
- находить значения функции, заданной формулой, таблицей, графиком по ее
аргументу; находить значение аргумента по значению функции, заданной графиком или
таблицей;
- определять свойства функции по ее графику; применять графические
представления при решении уравнений, систем, неравенств;
- описывать свойства изученных функций
строить их графики;
использовать приобретенные знания и умения в практической деятельности
и повседневной жизни для:
- выполнения расчетов по формулам, составления формул, выражающих
зависимости между реальными величинами; нахождения нужной формулы в справочных
материалах;
- моделирования практических ситуаций и исследование построенных моделей с
использованием аппарата алгебры;
- описания зависимостей между физическими величинами соответствующими
формулами при исследовании несложных практических ситуаций;
- интерпретации графиков реальных зависимостей между величинами.
Элементы логики, комбинаторики, статистики и теории вероятностей
уметь
- проводить несложные доказательства, получать простейшие следствия из
известных или ранее полученных утверждений, оценивать логическую правильность
рассуждений, использовать примеры для иллюстрации и контрпримеры для
опровержения утверждений;
- извлекать информацию, представленную в таблицах, на диаграммах, графиках;
составлять таблицы, строить диаграммы и графики;
- решать комбинаторные задачи путем систематического перебора возможных
вариантов, вычислять средние значения результатов измерений;
-находить частоту события, используя собственные наблюдения и готовые
статистические данные;
использовать приобретенные знания и умения в практической деятельности
и повседневной жизни для:
- выстраивания аргументации при доказательстве (в форме монолога и диалога);
- распознавания логически некорректных рассуждений;
- записи математических утверждений, доказательств;
- анализа реальных числовых данных, представленных в виде диаграмм,
графиков, таблиц;
- решения практических задач в повседневной и профессиональной деятельности
с использованием действий с числами, процентов, длин, площадей, объемов, времени,
скорости;
- решения учебных и практических задач, требующих систематического
перебора вариантов;
- понимания статистических утверждений.
Алгебра 7 класс
Автор учебника: Алимов Ш.А.
(3 ч. в неделю, всего 102 ч.)
| № урока | № урока в теме | Тема | Кол-во часов | Обеспеченность учебно – наглядными средствами обучения и оборудованием | Дата |
|
|
| Алгебраические выражения | 10 |
|
|
| 1 | 1 | Числовые выражения | 1 | Презентация | 2.09 |
| 2 | 2 | Алгебраические выражения | 1 | Презентация | 4.09 |
| 3-4 | 3-4 | Алгебраические равенства. Формулы | 2 | Презентация, карточки | 6.09 9.09 |
| 5-6 | 5-6 | Свойства арифметических действий | 2 | Презентация, карточки | 11.09 13.09 |
| 7-8 | 7-8 | Правила раскрытия скобок | 2 | Презентация, карточки | 16.09 18.09 |
| 9 | 9 | Обобщающий урок | 1 | Презентация | 20.09 |
| 10 | 10 | Контрольная работа №1 по теме «Алгебраические выражения»
| 1 |
| 23.09 |
|
|
| Уравнения с одним неизвестным | 8 |
|
|
| 11 | 1 | Уравнения и его корни | 1 | Презентация | 25.09 |
| 12-13 | 2-3 | Решение уравнений с одним неизвестным, сводящихся к линейным | 2 | Презентация, карточки | 27.09 30.09 |
| 14-16 | 4-6 | Решение задач с помощью уравнений | 3 | Презентация, карточки | 2.10 4.10 7.10 |
| 17 | 7 | Обобщающий урок | 1 | Презентация | 9.10 |
| 18 | 8 | Контрольная работа №2 по теме «Уравнения с одним неизвестным»
| 1 |
| 11.10 |
|
|
| Одночлены и многочлены | 17 |
|
|
| 19-20 | 1-2 | Степень с натуральным показателем | 2 | Презентация, карточки | 14.10 16.10 |
| 21-22 | 3-4 | Свойства степени с натуральным показателем | 2 | Презентация, карточки | 18.10 21.10 |
| 23 | 5 | Одночлен. Стандартный вид одночлена | 1 | Презентация | 23.10 |
| 24-25 | 6-7 | Умножение одночленов | 2 | Презентация, карточки | 25.10 28.10 |
| 26 | 8 | Многочлены | 1 | Презентация | 30.10 |
| 27 | 9 | Приведение подобных членов | 1 | Презентация, карточки | 1.11 |
| 28 | 10 | Сложение и вычитание многочленов | 1 | Презентация, карточки | 11.11 |
| 29 | 11 | Умножение многочлена на одночлен | 1 | Презентация, карточки | 13.11 |
| 30-31 | 12-13 | Умножение многочлена на многочлен | 2 | Презентация, карточки | 15.11 18.11 |
| 32-33 | 14-15 | Деление одночлена и многочлена на одночлен | 2 | Презентация, карточки | 20.11 22.11 |
| 34 | 16 | Обобщающий урок | 1 | Презентация | 25.11 |
| 35 | 17 | Контрольная работа №3 по теме «Одночлены и многочлены»
| 1 |
| 27.11 |
|
|
| Разложение многочлена на множители | 17 |
|
|
| 36-38 | 1-3 | Вынесение общего множителя за скобки | 3 | Презентация, карточки, тест | 29.11 2.12 4.12 |
| 39-41 | 4-6 | Способ группировки | 3 | Презентация, карточки | 6.12 9.12 11.12 |
| 42-44 | 7-9 | Формула разности квадратов | 3 | Презентация, карточки | 13.12 16.12 18.12 |
| 45-48 | 10-13 | Квадрат суммы. Квадрат разности | 4 | Презентация, карточки | 20.12 23.12 25.12 27.12 |
| 49-51 | 14-16 | Применение нескольких способов разложения многочлена на множители | 3 | Презентация, карточки | 13.01 15.01 17.01 |
| 52 | 17 | Контрольная работа №4 по теме «Разложение многочленов на множители»
| 1 |
| 20.01 |
|
|
| Алгебраические дроби | 20 |
|
|
| 53-55 | 1-3 | Алгебраическая дробь. Сокращение дробей | 3 | Презентация, карточки | 22.01 24.01 27.01 |
| 56-57 | 4-5 | Приведение дробей к общему знаменателю | 2 | Презентация, карточки | 29.01 31.01 |
| 58-62 | 6-10 | Сложение и вычитание алгебраических дробей | 5 | Презентация, карточки | 3.02 5.02 7.02 10.02 12.02 |
| 63-66 | 11-14 | Умножение и деление алгебраических дробей | 4 | Презентация, карточки | 14.02 17.02 19.02 21.02 |
| 67-71 | 15-19 | Совместные действия над алгебраическими дробями | 5 | Презентация, карточки | 24.02 26.02 28.02 3.03 5.03 |
| 72 | 20 | Контрольная работа №5 по теме «Алгебраические дроби»
| 1 |
| 7.03 |
|
|
| Линейная функция и её график | 10 |
|
|
| 73 | 1 | Прямоугольная система координат на плоскости | 1 | Презентация | 10.03 |
| 74-75 | 2-3 | Функция | 2 | Презентация | 12.03 14.03 |
| 76-78 | 4-6 | Функция и её график | 3 | Презентация, карточки | 17.03 19.03 21.03 |
| 79-81 | 7-9 | Линейная функция и её график | 3 | Презентация, карточки | 2.04 4.04 7.04 |
|
|
| Обобщающий урок | - |
| 9.04 |
| 82 | 10 | Контрольная работа №6 по теме «Линейная функция и ее график»
| 1 |
| 11.04 |
|
|
| Системы двух уравнений с двумя неизвестными | 11 |
|
|
| 83 | 1 | Системы уравнений | 1 | Презентация | 14.04 |
| 84-85 | 2-3 | Способ подстановки | 2 | Презентация, карточки | 16.04 18.04 |
| 86-88 | 4-6 | Способ сложения | 3 | Презентация | 21.04 23.04 25.04 |
| 89 | 7 | Графический способ решения систем уравнений | 1 | Презентация | 28.04 |
| 90-92 | 8-10 | Решение задач с помощью систем уравнений | 3 | Презентация | 30.04 2.05 5.05 |
|
|
| Обобщающий урок | - |
|
|
| 93 | 11 | Контрольная работа №7 по теме «Системы двух уравнений с двумя неизвестными»
| 1 |
| 7.05 |
|
|
| Элементы комбинаторики | 6 |
|
|
| 94-95 | 1-2 | Различные комбинации из трёх элементов | 2 | Презентация | 12.05 14.05 |
| 96-97 | 3-4 | Таблица вариантов и правило произведения | 2 | Презентация | 16.05 19.05 |
| 98 | 5 | Подсчёт вариантов с помощью графов | 1 | Презентация | 21.05 |
| 99 | 6 | Решение задач. Самостоятельная работа | 1 | тест | 23.05 |
|
100-102 |
|
Повторение. Итоговый зачет |
3 |
| 26.05 28.05 30.05 |
Алгебра 8 класс
Автор учебника: Алимов Ш.А.
(3 ч. в неделю, всего 102 ч.)
| № урока | № урока в теме | № параграфа | Тема | Кол-во часов | Обеспеченность учебно – наглядными средствами обучения и оборудованием | Дата | Корректировка программы |
|
|
|
| Глава 1. Неравенства | 19 |
|
|
|
| 1-2 | 1-2 | 1 | Положительные и отрицательные числа | 2 | Презентация |
|
|
| 3 | 3 | 2 | Числовые неравенства | 1 | Презентация |
|
|
| 4-5 | 4-5 | 3 | Основные свойства числовых неравенств | 2 | Презентация |
|
|
| 6 | 6 | 4 | Сложение и умножение числовых неравенств | 1 | Презентация |
|
|
| 7 | 7 | 5 | Строгие и нестрогие неравенства | 1 |
|
|
|
| 8 | 8 | 6 | Неравенства с одним неизвестным | 1 | Презентация, линейка |
|
|
| 9-11 | 9-11 | 7 | Решение неравенств | 3 | Презентация, линейка |
|
|
| 12 | 12 | 8 | Системы неравенств с одним неизвестным. Числовые промежутки | 1 | Презентация, линейка |
|
|
| 13-15 | 13-15 | 9 | Решение систем неравенств | 3 | Презентация, линейка |
|
|
| 16-17 | 16-17 | 10 | Модуль числа. Уравнения и неравенства, содержащие модуль | 2 | Презентация, линейка |
|
|
| 18 | 18 |
| Обобщающий урок | 1 | Презентация, линейка |
|
|
| 19 | 19 |
| Контрольная работа №1 | 1 |
|
|
|
|
|
|
| Глава 2. Приближённые вычисления | 14ч |
|
|
|
| 20-21 | 1-2 | 11 | Приближённые значения величин. Погрешность приближения | 2 | Микрокалькулятор |
|
|
| 22-23 | 3-4 | 12 | Оценка погрешности | 2 | Микрокалькулятор |
|
|
| 24 | 5 | 13 | Округление чисел | 1 | Микрокалькулятор |
|
|
| 25-26 | 6-7 | 14 | Относительная погрешность | 2 | Микрокалькулятор |
|
|
| 27-28 | 8-9 | 15 | Практические приемы приближенных вычислений | 2 | Микрокалькулятор |
|
|
| 29 | 10 | 16 | Простейшие вычисления на микрокалькуляторе | 1 | Микрокалькулятор |
|
|
| 30-31 | 11-12 | 17 | Действия над числами, записанными в стандартном виде | 2 | Микрокалькулятор |
|
|
| 32 | 13 | 18 | Вычисления на микрокалькуляторе степени и числа, обратного данному | 1 | Микрокалькулятор |
|
|
| 33 | 14 | 19 | Последовательное выполнение операций на микрокалькуляторе
| 1 | Микрокалькулятор |
|
|
|
|
|
| Глава 3. Квадратные корни | 14 |
|
|
|
| 34-35 | 1-2 | 20 | Арифметический квадратный корень | 2 | Презентация |
|
|
| 36-37 | 3-4 | 21 | Действительные числа | 2 | Презентация |
|
|
| 38-40 | 5-7 | 22 | Квадратный корень из степени | 3 | Презентация |
|
|
| 41-42 | 8-9 | 23 | Квадратный корень из произведения | 2 | Презентация |
|
|
| 43-44 | 10-11 | 24 | Квадратный корень из дроби | 2 | Презентация |
|
|
| 45-46 | 12-13 |
| Обобщающий урок | 2 | Презентация |
|
|
| 47 | 14 |
| Контрольная работа №2 | 1 |
|
|
|
|
|
|
| Глава 4. Квадратные уравнения | 23 |
|
|
|
| 48-49 | 1-2 | 25 | Квадратное уравнение и его корни | 2 | Презентация |
|
|
| 50 | 3 | 26 | Неполные квадратные уравнения | 1 | Презентация |
|
|
| 51 | 4 | 27 | Метод выделения полного квадрата | 1 | Презентация |
|
|
| 52-54 | 5-7 | 28 | Решение квадратных уравнений | 3 | Презентация |
|
|
| 55-57 | 8-10 | 29 | Приведённое квадратное уравнение. Теорема Виета. Проверочная работа. | 3 | Презентация |
|
|
| 58-60 | 11-13 | 30 | Уравнения, сводящиеся к квадратным | 3 | Презентация |
|
|
| 61-64 | 14-17 | 31 | Решение задач с помощью квадратных уравнений | 4 | Презентация |
|
|
| 65-67 | 18-20 | 32 | Решение простейших систем, содержащих уравнение второй степени | 3 | Презентация |
|
|
| 68-69 | 21-22 |
| Обобщающий урок | 2 | Презентация |
|
|
| 70 | 23 |
| Контрольная работа №3 | 1 |
|
|
|
|
|
|
| Глава 5. Квадратичная функция | 16ч |
|
|
|
| 71 | 1 | 35 | Определение квадратичной функции | 1 | Презентация, линейка, треугольник |
|
|
| 72 | 2 | 36 | Функция y=x2 | 1 | Презентация, линейка, треугольник |
|
|
| 73-75 | 3-5 | 37 | Функция y=ax2 | 3 | Презентация, линейка, треугольник |
|
|
| 76-78 | 6-8 | 38 | Функция y=ax2+bx+c | 3 | Презентация, линейка, треугольник |
|
|
| 79-83 | 9-13 | 39 | Построение графика квадратичной функции | 5 | Презентация, линейка, треугольник |
|
|
| 84-85 | 14-15 |
| Обобщающий урок | 2 | Презентация, линейка, треугольник |
|
|
| 86 | 16 |
| Контрольная работа №4 | 1 |
|
|
|
|
|
|
| Глава 6. Квадратные неравенства | 12ч |
|
|
|
| 87-88 | 1-2 | 40 | Квадратное неравенство и его решение | 2 | Презентация |
|
|
| 89-93 | 3-7 | 41 | Решение квадратного неравенства с помощью графика квадратичной функции | 5 | Презентация, линейка |
|
|
| 94-95 | 8-9 | 42 | Метод интервалов | 2 | Презентация, линейка |
|
|
| 96 | 10 | 43* | Исследование квадратного трёхчлена | 1 | Презентация, линейка |
|
|
| 97 | 11 |
| Обобщающий урок | 1 | Презентация, линейка |
|
|
| 98 | 12 |
| Контрольная работа №5 | 1 |
|
|
|
| 99-102 | 1-4 |
| Повторение. Итоговый зачет | 4 |
|
|
|
Алгебра 9 класс
Автор учебника: Алимов Ш.А.
( 3 часа в неделю. Всего 102 часа)
| № урока | № урока в теме | Тема | Кол-во часов | Обеспеченность учебно – наглядными средствами обучения и оборудованием | Дата |
| 1-3 | 1-3 | Повторение курса алгебры 8 класса | 3ч | Презентация
| 2.09 3.09 4.09 9.09 |
|
|
| Глава 1. Алгебраические уравнения Системы нелинейных уравнений. | 15ч |
|
|
| 4 | 1 | Деление многочленов | 1ч | Презентация | 10.09 |
| 5-6 | 2-3 | Решение алгебраических уравнений | 2ч | Презентация
| 11.09 12.09 |
| 7-9 | 4-6 | Уравнения, сводящиеся к алгебраическим. | 3ч | Презентация
| 16.09 17.09 18.09 |
| 10-12 | 7-9 | Системы нелинейных уравнений с двумя неизвестными | 3ч | Презентация
| 23.09 24.09 25.09 |
| 13-14 | 10-11 | Различные способы решения систем уравнений | 2ч | Презентация | 30.09 1.10 |
| 15-16 | 12-13 | Решение задач с помощью систем уравнений | 2ч | Презентация | 2.10 7.10 |
| 17 | 14 | Обобщающий урок | 1ч |
|
|
| 18 | 15 | Контрольная работа №1 «Алгебраические уравнения. Системы нелинейных уравнений» | 1ч |
| 8.10 |
|
|
| Глава 2. Степень с рациональным показателем | 10ч |
|
|
| 19-21 | 1-3 | Степень с целым показателем | 3ч | Презентация
| 9.10 14.10 15.10 |
| 22-23 | 4-5 | Арифметический корень натуральной степени. | 2ч | Презентация
| 16.10 21.10 |
| 24-25 | 6-7 | Свойства арифметического корня | 2ч | Презентация | 22.10 23.10 |
| 26 | 8 | Степень с рациональным показателем. | 1ч | Презентация | 28.10 |
| 27 | 9 | Возведение в степень числового неравенства | 1ч | Презентация | 29.10 |
| 28 | 10 | Контрольная работа №2 «Степень с рациональным показателем» | 1ч |
| 30.10 |
|
|
| Глава 3. Степенная функция
| 17ч |
|
|
| 29-31 | 1-3 | Область определения функции | 3ч | Презентация | 11.11 12.11 13.11 |
| 32-33 | 4-5 | Возрастание и убывание функции | 2ч | Презентация | 18.11 19.11 |
| 34-35 | 6-7 | Чётность и нечётность функции | 2ч | Презентация | 20.11 25.11 |
| 36-38 | 8-10 | Функция y= k/x | 3ч | Презентация
| 26.11 27.11 2.12 |
| 39-42 | 11-14 | Неравенства и уравнения, содержащие степень | 4ч | Презентация | 3.12 4.12 9.12 10.12 |
| 43-44 | 15-16 | Обобщающие уроки | 2ч |
| 11.12 16.12 |
| 45 | 17 | Контрольная работа № 3 «Степенная функция» | 1ч |
| 17.12 |
|
|
| Глава 4. Прогрессии
| 14ч |
|
|
| 46 | 1 | Числовая последовательность | 1ч | Презентация | 18.12 |
| 47-48 | 2-3 | Арифметическая прогрессия | 2ч | Презентация | 23.12 24.12 |
| 49-51 | 4-6 | Сумма n первых членов арифметической прогрессии | 3ч | Презентация
| 25.12 13.01 14.01 |
| 52-54 | 7-9 | Геометрическая прогрессия | 3ч | Презентация
| 15.01 20.01 21.01 |
| 55-57 | 10-12 | Сумма n первых членов геометрической прогрессии | 3ч | Презентация
| 22.01 27.01 28.01 |
| 58 | 13 | Обобщающий урок | 1ч |
| 29.01 |
| 59 | 14 | Контрольная работа №4 «Прогрессии» | 1ч |
| 3.02 |
|
|
| Глава 5. Случайные события | 11ч |
|
|
| 60 | 1 | События | 1ч | Презентация | 4.02 |
| 61-62 | 2-3 | Вероятность события. | 2ч | Презентация | 5.02 10.02 |
| 63-64 | 4-5 | Решение вероятностных задач с помощью комбинаторики. | 2ч | Презентация | 11.02 12.02 |
| 65 | 6 | Геометрическая вероятность | 1ч | Презентация | 17.02 |
| 66-68 | 7-9 | Относительная частота и закон больших чисел | 3ч | Презентация | 18.02 19.02 24.02 |
| 69 | 10 | Обобщающий урок | 1ч |
| 25.02 |
| 70 | 11 | Контрольная работа №5 «Случайные события» | 1ч |
| 26.02 |
|
|
| Глава 6. Случайные величины
| 12ч |
|
|
| 71-73 | 1-3 | Таблицы распределения | 3ч | Презентация | 3.03 4.03 5.03 |
| 74-75 | 4-5 | Полигоны частот | 2ч | Презентация | 10.03 11.03 |
| 76-77 | 6-7 | Генеральная совокупность и выборка | 2ч | Презентация | 12.03 17.03 |
| 78-80 | 8-10 | Размах и центральные тенденции | 3ч | Презентация | 18.03 19.03 1.04 |
| 81 | 11 | Обобщающий урок | 1ч |
| 2.04 |
| 82 | 12 | Контрольная работа №6 «Случайные величины» | 1ч |
| 7.04 |
|
|
| Глава 7. Множества, логика
| 11ч |
|
|
| 83-84 | 1-2 | Множества | 2ч | Презентация | 8.04 9.04 |
| 85 | 3 | Высказывания. Теоремы | 1ч | Презентация | 14.04 |
| 86-87 | 4-5 | Уравнение окружности | 2ч | Презентация | 15.04 16.04 |
| 88-89 | 6-7 | Уравнение прямой | 2ч | Презентация | 21.04 22.04 |
| 90-91 | 8-9 | Множества точек на координатной плоскости | 2ч | Презентация | 23.04 28.04 |
| 92 | 10 | Обобщающий урок. | 1ч |
| 29.04 |
| 93 | 11 | Контрольная работа №7 «Множества, логика» | 1ч |
| 30.04 |
| 94-102 |
| Повторение курса алгебры | 8ч | Презентации | 5.05 6.05 7.05 12.05 13.05 14.05 19.05 20.05 21.05 |
Критерии и нормы оценки результатов обучения обучающихся
Для оценки достижений учащихся применяется пятибалльная система оценивания.
Нормы оценки:
1. Оценка письменных контрольных работ обучающихся по алгебре.
Ответ оценивается отметкой «5», если:
1) работа выполнена полностью;
2) в логических рассуждениях и обосновании решения нет пробелов и ошибок;
3) в решении нет математических ошибок (возможна одна неточность, описка, которая
не является следствием незнания или непонимания учебного материала).
Отметка «4» ставится, если:
1) работа выполнена полностью, но обоснования шагов решения недостаточны (если
умение
обосновывать рассуждения не являлось специальным объектом проверки);
2)допущены одна ошибка или есть два – три недочёта в выкладках, рисунках, чертежах
или графиках (если эти виды работ не являлись специальным объектом проверки).
Отметка «3» ставится, если:
1) допущено более одной ошибки или более двух – трех недочетов в выкладках,
чертежах
или графиках, но обучающийся обладает обязательными умениями по проверяемой теме.
Отметка «2» ставится, если:
1) допущены существенные ошибки, показавшие, что обучающийся не обладает
обязательными умениями по данной теме в полной мере.
2.Оценка устных ответов обучающихся по алгебре
Ответ оценивается отметкой «5», если ученик:
- полно раскрыл содержание материала в объеме, предусмотренном программой и
учебником;
- изложил материал грамотным языком, точно используя математическую терминологию
и символику, в определенной логической последовательности, правильно выполнил рисунки,
чертежи, графики, сопутствующие ответу;
- показал умение иллюстрировать теорию конкретными примерами, применять ее в
новой ситуации при выполнении практического задания;
- продемонстрировал знание теории ранее изученных сопутствующих тем,
сформированность и устойчивость используемых при ответе умений и навыков;
- отвечал самостоятельно, без наводящих вопросов учителя;
- возможны одна – две неточности при освещение второстепенных вопросов или в
выкладках, которые ученик легко исправил после замечания учителя.
Ответ оценивается отметкой «4»,
если удовлетворяет в основном требованиям на оценку «5», но при этом имеет один из
недостатков:
- в изложении допущены небольшие пробелы, не исказившее математическое
содержание ответа;
- допущены один – два недочета при освещении основного содержания ответа,
исправленные после замечания учителя;
- допущены ошибка или более двух недочетов при освещении второстепенных вопросов
или в выкладках, легко исправленные после замечания учителя.
Отметка «3» ставится в следующих случаях:
- неполно раскрыто содержание материала (содержание изложено фрагментарно, не
всегда последовательно), но показано общее понимание вопроса и продемонстрированы
умения, достаточные для усвоения программного материала (определены «Требованиями к
математической подготовке учащихся» в настоящей программе по алгебре);
- имелись затруднения или допущены ошибки в определении математической
терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов
учителя;
- ученик не справился с применением теории в новой ситуации при выполнении
практического задания, но выполнил задания обязательного уровня сложности по данной
теме;
- при достаточном знании теоретического материала выявлена недостаточная
сформированность основных умений и навыков.
Отметка «2» ставится в следующих случаях:
- не раскрыто основное содержание учебного материала;
- обнаружено незнание учеником большей или наиболее важной части учебного
материала;
- допущены ошибки в определении понятий, при использовании математической
терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов
учителя.
Итоговая оценка знаний, умений и навыков
1. За учебную четверть и за год знания, умения и навыки учащихся по математике
оцениваются одним баллом.
2. Основанием для выставления итоговой оценки знаний служат результаты
наблюдений учителя за повседневной работой учеников, устного опроса, текущих и
итоговых контрольных работ. Однако последним придается наибольшее значение.
3. При выставлении итоговой оценки учитывается как уровень теоретических знаний
ученика, так и овладение им практическими умениями и навыками. Однако ученику не
может быть выставлена положительная итоговая оценка по математике, если все или
большинство его текущих обучающих и контрольных работ, а также итоговая
контрольная работа оценены как неудовлетворительные, хотя его устные ответы оценивались
положительно.
Учебно — методический комплект:
для учителя:
Алимов Ш.А. Алгебра. Учебник для 7, 8, 9 классов общеобразовательных учреждений.М., «Просвещение», 2013.
Дорофеев Г. В. и др. Оценка качества подготовки выпускников основной школы по математике. М., «Дрофа», 2001.
Программы общеобразовательных учреждений. Алгебра. 7-9 классы. Составитель: Бурмистрова Татьяна Антоновна, «Просвещение» Москва 2008
Разноуровневые дидактические материалы по алгебре. 8 класс. / Н.Г. Миндюк, М.Б. Миндюк. / М.: Генжер, 1999. – 95 с.
Уроки алгебры в 9 классе. / В.И. Жохов, Л.Б. Крайнева. Пособие для учителей. / М.: Вербум – М, 2000.
для учащихся:
Алимов Ш.А. Алгебра. Учебник для 7, 8, 9 классов общеобразовательных учреждений. М., «Просвещение», 2013

 Получите свидетельство
Получите свидетельство Вход
Вход



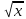 , у=
, у=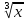 , у=
, у=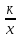 , обогащая опыт выполнения знаково-символических действий. Строить речевые конструкции с использованием функциональной терминологии. Исследования графиков функций в зависимости от значений коэффициентов, входящих в формулу. Распознавать виды изучаемых функций. Строить графики указанных функций (в том числе с применением движения графиков); описывать их свойства. Решать простейшие уравнения и неравенства, содержащие степень. Решать иррациональные уравнения.
, обогащая опыт выполнения знаково-символических действий. Строить речевые конструкции с использованием функциональной терминологии. Исследования графиков функций в зависимости от значений коэффициентов, входящих в формулу. Распознавать виды изучаемых функций. Строить графики указанных функций (в том числе с применением движения графиков); описывать их свойства. Решать простейшие уравнения и неравенства, содержащие степень. Решать иррациональные уравнения.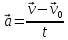 и
и 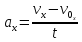
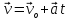 ,
, 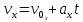 ,
, 
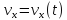
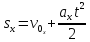
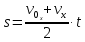
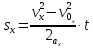
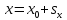 может быть преобразовано в уравнение
может быть преобразовано в уравнение 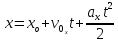
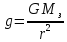
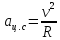
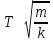
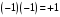 ?
?








 Рабочая программа по физике. ФГОС ООО.7-9 классы (2.48 MB)
Рабочая программа по физике. ФГОС ООО.7-9 классы (2.48 MB)
 0
0 384
384 4
4 Нравится
0
Нравится
0


