Прзентация к уроку Решения систем двух линейных уравнений с двумя переменными,

Урок

математики

12.01.18

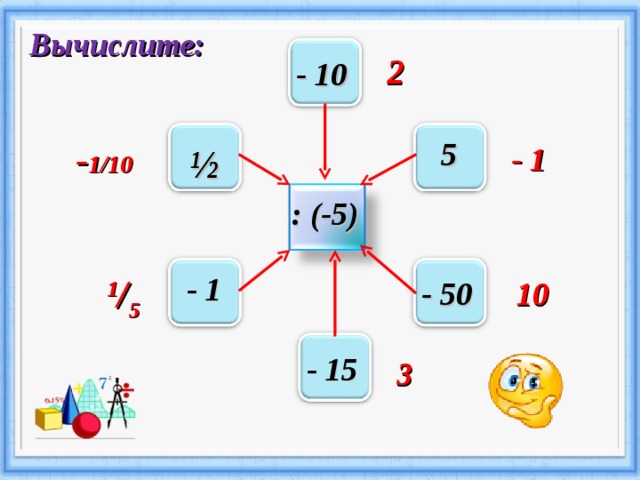
Вычислите:

2

- 10

5

- 1/10

½

- 1

: (-5)

- 1

1 / 5

- 50

10

- 15

3

Раскройте скобки:

-(6-9у)

-6 + 9у

7(2х-5)

14х – 35

-3(8+9а)

-24 – 27а

12.01.18

3

Выразить у через х:

Х+У=4

У=4-Х

2Х-У=3

У=2Х-3

Выразить х через у :

Х+2У=5

Х=5-2У

3Х-2У=4

Х=(4+2У)/3

12.01.18

Точный бросок

вычислите значение

у=4х-7 , если :

х=0

х= 2

1

-7

х= 1

х=-1

-3

-11

654

20.05.16. Классная работа.

«Решение систем двух уравнений

с двумя неизвестными».

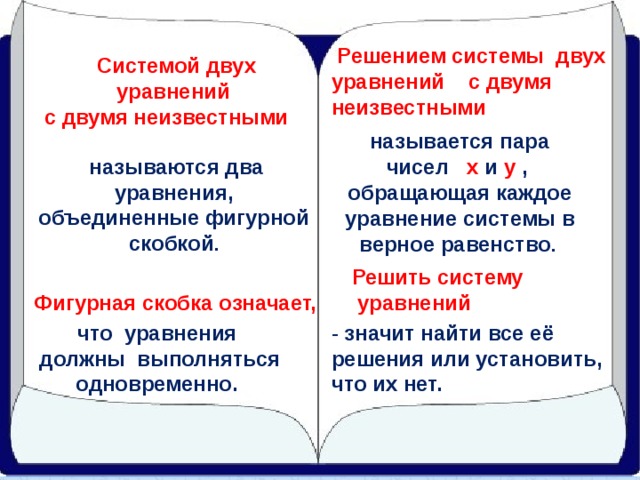
Решением системы двух уравнений с двумя неизвестными

Системой двух уравнений

с двумя неизвестными

называется пара

чисел х и у ,

обращающая каждое уравнение системы в верное равенство .

называются два уравнения, объединенные фигурной скобкой .

Решить систему

уравнений

Фигурная скобка означает,

что уравнения

должны выполняться одновременно.

- значит найти все её решения или установить, что их нет.

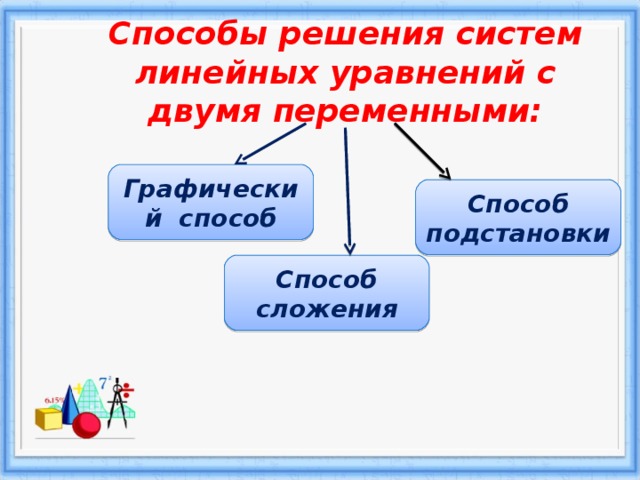
Способы решения систем линейных уравнений с двумя переменными:

Графический способ

Способ подстановки

Способ сложения

ГРАФИЧЕСКИЙ СПОСОБ

1. Выражают У через Х в каждом уравнении;

2. Строят графики каждого уравнения в одной системе координат;

3. Определяют координаты точки пересечения этих графиков;

4. Записывают ответ: Х=…, У=…, или (Х, У)

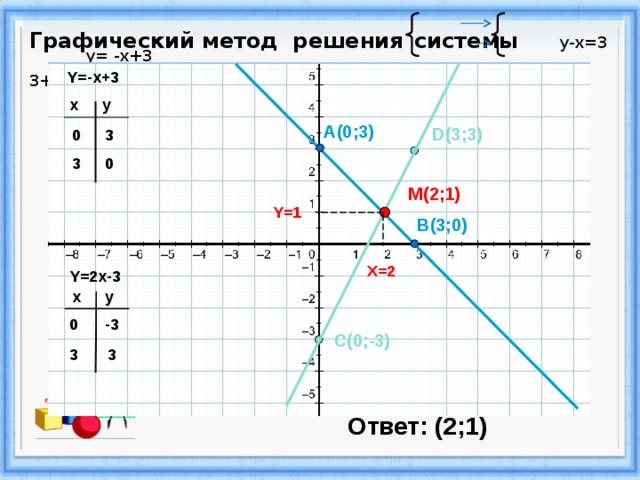
Графический метод решения системы у-х=3 y= -x+3 3+у=2х y= 2x-3

Y=-x+3

x

y

A(0;3)

D(3;3)

3

0

0

3

M(2;1)

Y=1

B(3;0)

X=2

Y=2x-3

x

y

0

-3

C(0;-3)

3

3

Ответ: (2;1)

Решите систему графическим способом

2х + у = 7

3х - 2у = 0

12.01.18

12.01.18

СПОСОБ ПОДСТАНОВКИ

1. Из одного уравнения выражают одну переменную через другую.

2. Подставляют во второе уравнение найденное выражение.

3. Решают полученное уравнение с одной переменной.

4. Находят соответствующее значение другой переменной.

Решим систему 3х + 2у = 4

х – 4у = 6

1. Из второго уравнения выражаем x = 4 y+6

2 .Подставляем данное выражение в первое уравнение: 3( 4 y+6) + 2y=4

3. Решаем уравнение 12y+18+2y=4

14y = -14

y=-1

4. Находим х: x=4∙(-1)+6

x=2

Ответ: (2;-1)

Решите систему способом подстановки

2х + у = 7

3х - 2у = 0

12.01.18

СПОСОБ СЛОЖЕНИЯ

1. Умножают левую и правую части одного или обоих уравнений на некоторое число так, чтобы коэффициенты при одной из переменных в разных уравнениях стали противоположными числами ;

2. Складывают почленно полученные уравнения;

3. Решают полученное уравнение с одной переменной;

4. Находят соответствующее значение второй

переменной.

Решим систему:

2х – 3у = 11

3х + 7у = 5

1 Первое уравнение умножим на (-3), а второе - на 2

- 6х + 9у = - 33

6х + 14у = 10

2 . Соложим полученные уравнения

23 y = -23

y =-1

3. Найдем х : 2x - 3· (-1) =11

2 x + 3 = 11

2х = -3 +11

2х = 8

х = 4

Ответ: ( 4 ;- 1 )

1.

Решите систему способом сложения

2х + у = 7

3х - 2у = 0

12.01.18

Вывод:

Итак, одну и ту же систему можно решить разными способами.

Какой из них вам показался более удобным?

В чем недостаток каждого метода?

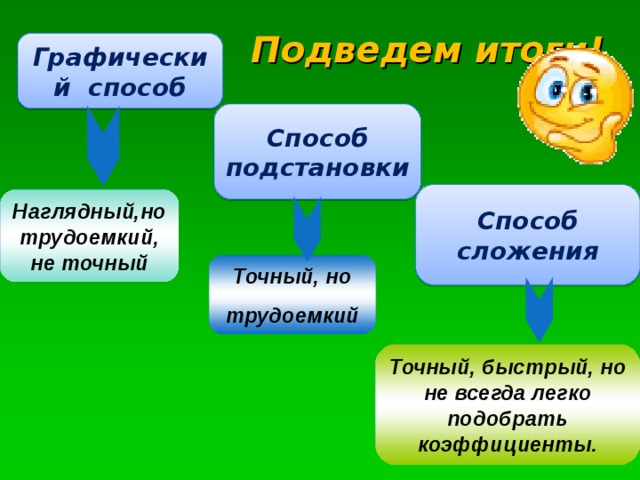
Подведем итоги!

Графический способ

Способ подстановки

Способ сложения

Наглядный,но трудоемкий, не точный

Точный, но

трудоемкий

Точный, быстрый, но не всегда легко подобрать коэффициенты.

Физминутка (коррекция зрения)

Ребята, чаще делайте физминутки для глаз!

Берегите свое зрение!!!

Самостоятельная работа.

Домашняя работа

Решить систему

2х+3у=7

6х-2у=10

удобным для вас способом

12.01.18

Продолжи предложение:

Сегодня на уроке я научился ………………………………..

Мне понравилось …………………………………………….

Я повторил …………………………………............................

Я закрепил ………………………………….............................

Я оценил бы свою работу на уроке на (хор., отл., удовл.)

СПАСИБО ЗА

РАБОТУ!