Проверка домашнего задания

Департамент образования города Москвы Северо-Западное окружное управление образования

Методическое объединение учителей математики ГБОУ СОШ № 1056. Проверка домашнего задания.

ФОРМЫ И МЕТОДЫ ОРГАНИЗАЦИИ ЭТАПА ВСЕСТОРОННЕЙ ПРОВЕРКИ ДОМАШНЕГО ЗАДАНИЯ.

“ Фактически постепенно должна стираться грань между классными и домашними заданиями с переходом к непрерывной, индивидуальной самостоятельной учебной

деятельности школьника”.

Эльконин – Давыдов

Организация этапа проверки

• Дидактическая задача
• Содержание
• Условия достижения положительных результатов
• Показатели выполнения дидактической задачи
• Требования
• Способы активации
• Ошибки, допускаемые

при реализации

Систематичность выполнения

Уровень усвоения учебного материала

Задача учителя

на

данном

этапе

Степень самостоятельности ученика

Виды домашней работы

• Индивидуальная
• Групповая
• Творческая
• Дифференцированная
• Одна на весь класс
• Составление домашней работы для пар постоянного состава

Рецензирование устного ответа

Диктант на основе домашнего упражнения

Краткий письменный ответ на вопрос

Проверка с помощью ИКТ

Постановка неожиданных вопросов

Инновационные методы проверки домашнего задания

Формы контроля домашнего задания

• Контроль письменных домашних заданий
• Косвенный контроль
• Контроль устных

домашних заданий

• Внеурочная проверка

тетрадей

• Непрямой контроль
• Взаимный контроль
• Самоконтроль

Фронтальная проверка домашнего задания у всего класса

• Проверка тетрадей с выполненным домашним заданием у всего класса;
• Проверка заданий на доске с заготовкой:

• учителем;
• учениками на перемене;
• учениками на кодоскопе;
• Устный опрос теоретического материала

• Самостоятельная работа по материалам домашней работы ;
• Ответы на вопросы домашнего задания, вызвавшие затруднения;
• Индивидуальная проверка по карточкам;
• Расшифровка текста по ответам домашнего задания;
• Работа в парах с взаимопроверкой

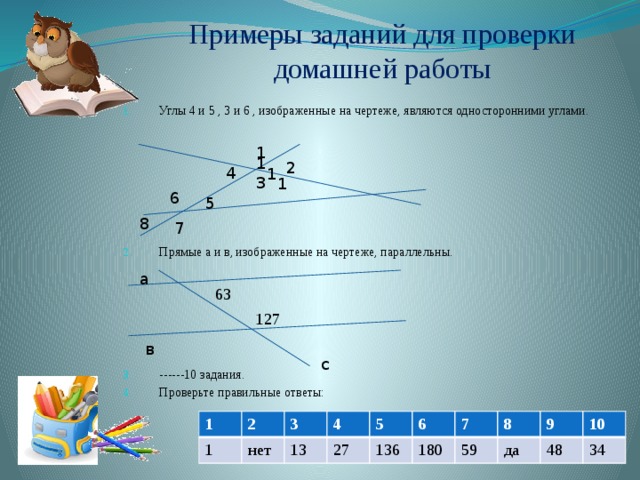
Примеры заданий для проверки домашней работы

• Углы 4 и 5 , 3 и 6 , изображенные на чертеже, являются односторонними углами.

• Прямые а и в, изображенные на чертеже, параллельны.

• ------10 задания.
• Проверьте правильные ответы:

1

1

2

4

1

3

1

6

5

8

7

а

63

127

в

с

1

2

1

3

нет

4

13

5

27

6

136

7

180

8

59

9

да

10

48

34

Восполните пробелы так, чтобы высказывание стало верным

• Две прямые на плоскости называются параллельными, если они ______________.
• Если при пересечении двух прямых секущей сумма _________ углов равна _________, то прямые параллельны.
• Через точку, не лежащую на данной прямой, проходит _______________ прямая, параллельная данной.

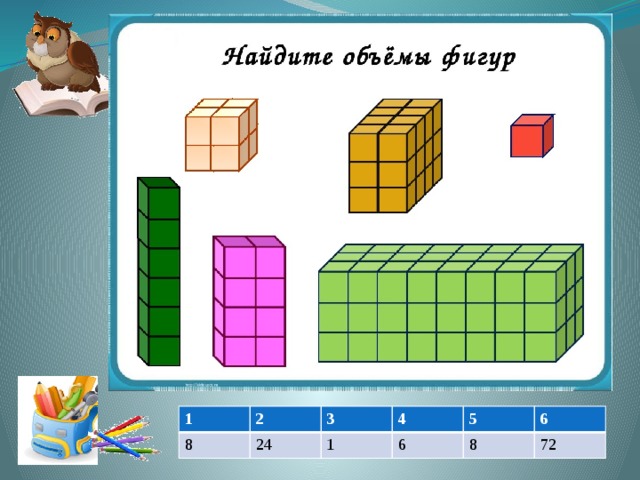
1

8

2

3

24

1

4

5

6

6

8

72

D 1

D 1

D 1

C 1

C 1

C 1

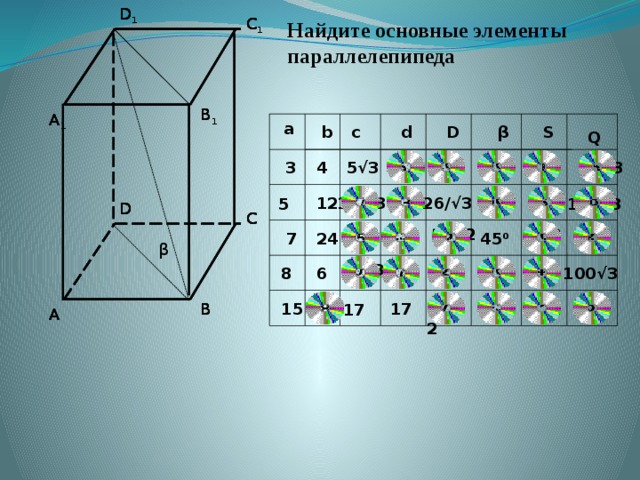
Найдите основные элементы

параллелепипеда

B 1

B 1

B 1

A 1

A 1

A 1

a

β

b

S

D

d

c

Q

10

60 0

25 √3

4

3

12

5

5 √3

30 0

30 0

30 0

13/ √3

60

13

60

26/ √3

12

169 √3

5

D

D

D

C

C

C

25 √2

25 √2

25

168

625

25

7

24

25

45 0

β

48

60 0

10 √3

20

100 √3

8

6

10

289

45 0

17

15

8

17 √2

B

B

B

17

120

120

A

A

A

D 1

C 1

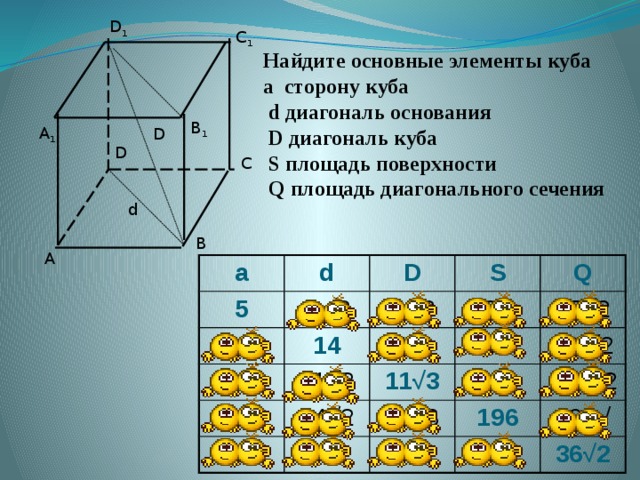
Найдите основные элементы куба

a сторону куба

d диагональ основания

D диагональ куба

S площадь поверхности

Q площадь диагонального сечения

B 1

A 1

D

D

C

d

B

A

a

5

d

7 √2

D

5 √2

11

S

5 √3

14

Q

25

11 √2

7√6

14

6

25 √2

98

11 √3

14 √2

121

98 √2

14 √3

6 √2

121 √2

196

6 √3

196 √

36

36 √2

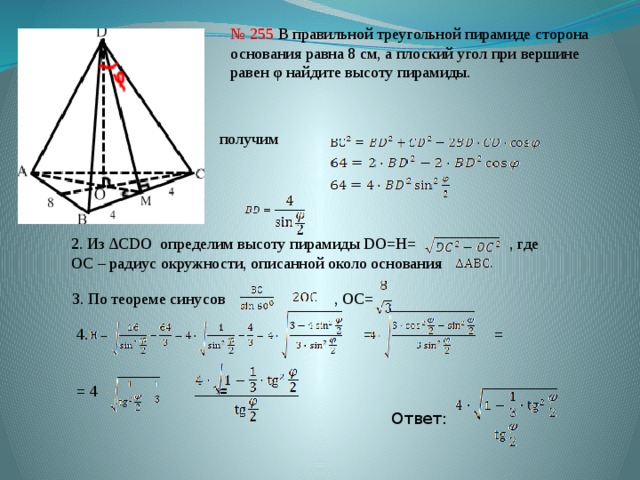
№ 255 В правильной треугольной пирамиде сторона основания равна 8 см, а плоский угол при вершине равен φ найдите высоту пирамиды.

получим

2. Из ΔCDO определим высоту пирамиды DO=H= , где ОС – радиус окружности, описанной около основания

3. По теореме синусов , ОС=

4. = =

= 4 =

Ответ:

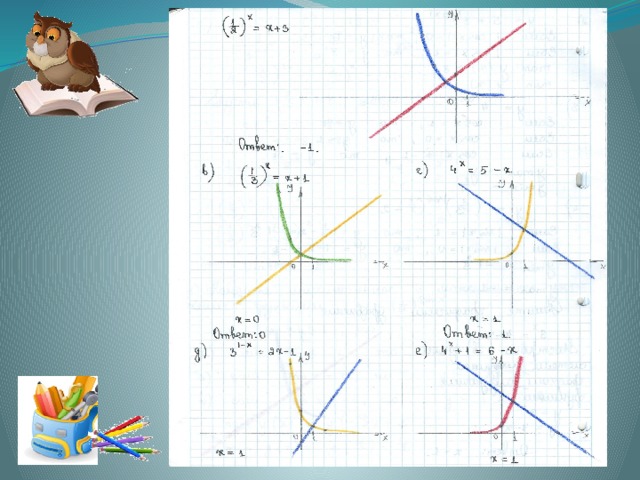
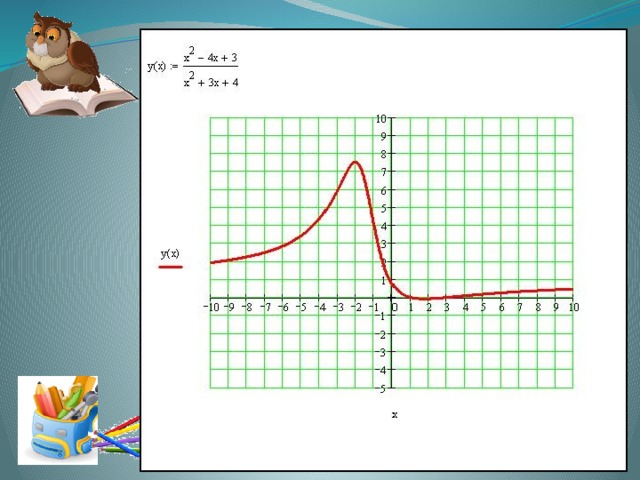
• cos 2 t=
• 1+tg²t=
• sin(a+r)=
• cos 30  =
• 1-sin²t=
• tg 60  =
• Какой знак имеет sin t в первой координатной четверти?
• cos (- t ) =
• 1 – cos t =
• sin2t=  3  2

• Убедитесь, что заданное Вами на дом домашнее задание Вы сможете потом проверить и оценить !

Древняя японская мудрость гласит:

Всматривайтесь в привычное - и вы увидите неожиданное.

Всматривайтесь в простое – и вы увидите сложное .

Всматривайтесь в малое - и вы увидите великое .

Благодарим за внимание.