Простые вопросы в сложной математике
Основная задача обучения математике в школе - прочное и осознанное овладение учащимися системой математических знаний и умений, необходимых в повседневной жизни и трудовой деятельности . Увеличение умственной нагрузки на уроках заставляет задуматься над тем, как поддержать интерес ученика к изучаемому материалу и его познавательную активность на протяжении всего урока.
Все годы работы я стараюсь искать эффективные методы обучения и приемы, которые активизировали бы мысль школьников, стимулировали развитие общей активности, самостоятельности, учащихся разного возраста. Приведу слова Д. Пойа о том, что «Обучение – это ремесло, использующее бесчисленное количество маленьких трюков».
Я не открою ничего нового если скажу, что математика даётся далеко не всем и далеко не так как нам хочется. И я хочу поделиться с вами маленькими хитростями, которые помогают моим ученикам легче запомнить и усвоить материал, а мне разнообразить работу на уроке и поддержать интерес к получению знаний.
И так, начинаем урок…. Коллеги, ответьте, пожалуйста, на вопрос: «Когда чёрной кошке проще всего зайти в дверь?». Я уверена, что вы ответили по разному. Но многие дети отвечают что ночью. А нет… Математика –это логика. Войти всегда легче когда открыта дверь и независимо какого цвета кошка. С помощью таких вопросов можно активизировать внимание ребят в начале урока.
Так же для активизации внимания и повторения пройденного материала я часто использую приём «Раскручивание темы». Например, тема урока «Свойства серединного перпендикуляра к отрезку». Здесь происходит и повторение уже известных понятий отрезок, перпендикуляр, середина отрезка и дети видят что нового они ещё могут узнать на предстоящем уроке.
При проверке домашних заданий мне очень нравится использовать такой вид активизации познавательной деятельности как «Найди ошибку исправь её». И когда я задаю такое задание, то мои ученики знают, что нужно воспользоваться методом «пристального взгляда», который я считаю очень важным в изучении математики.
А вот чтобы новый материал хорошо запомнился ученикам ,их нужно чем-то удивить, заинтриговать, вызвать положительные эмоции. У меня набран большой багаж приёмов нестандартного понимания и запоминания математического материала, который я применяю на своих уроках и на некоторых из них я сейчас остановлюсь.
Мне очень нравится правила «фонтанчик». Как вы уже догадались речь идёт о правилах умножения одночлена на многочлен. На первых парах мы «фонтанчик» рисуем, а потом остаётся только ключевая фраза.
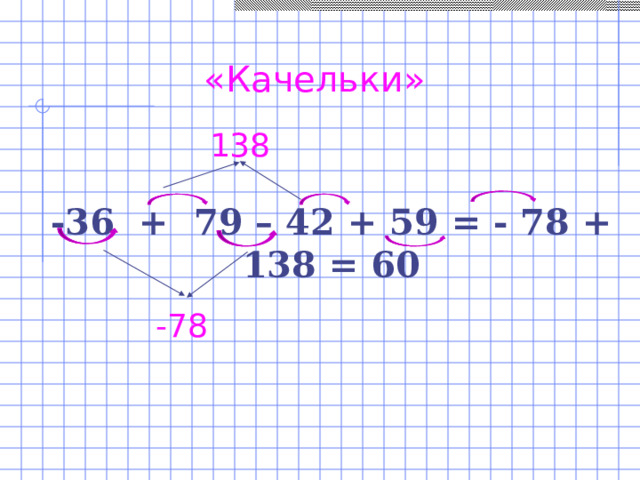
Известно, как нелегко формируются у ребят навыки сложения положительных и отрицательных чисел. Даже ученик, четко отвечающий правило, при решении упражнений нередко ошибается. Для отработки навыков счёта я применяю приём «качельки».
Уравнения всегда вызывают у ребят стресс. Снять тревогу мне помогают простые приёмы.
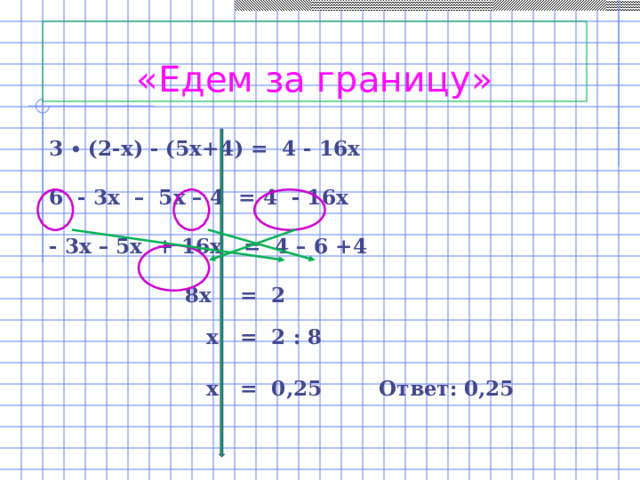
При переносе слагаемых из одной части уравнения в другую ребята очень часто допускают ошибку, забывая менять знаки на противоположные. Я предлагаю им под знаком “=” подразумевать границу нашей страны. Чтобы поехать за границу нам обязательно нужно поменять российский паспорт. И решая уравнения, нужно внимательно определить, “едет” ли данное слагаемое за границу или только меняет место жительства в стране (оставляем с тем же знаком).А «качельки» и «фонтанчик» нам помогут в решении этого уравнения.
При решении дробных рациональных уравнений учащиеся не понимают, почему сначала нужно знаменатель приравнять к нулю, хотя на ноль делить нельзя, найти нули знаменателя, а потом знак «равно» перечеркнуть. Я применяю такое образное сравнение. Ноль – это скрывшийся в знаменателе враг. Прежде чем его уничтожить, нам необходимо его найти. Находим ноль знаменателя, а потом его уничтожаем. Занимательно, а главное понятно.
Если бы я смогла присуждать нобелевскую премию по математике, то её бы получили теорема Пифагора и квадратное уравнение. Без этих знаний освоение в дальнейшем математики невозможно. При изучении темы «Квадратные уравнения» использую прием, когда можно, не решая, сразу определить корни уравнения: если сумма коэффициентов равна нулю, то первый корень обязательно единица, а другой равен 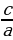 . Детям это очень нравится. Они всегда видят такие уравнени.
. Детям это очень нравится. Они всегда видят такие уравнени.
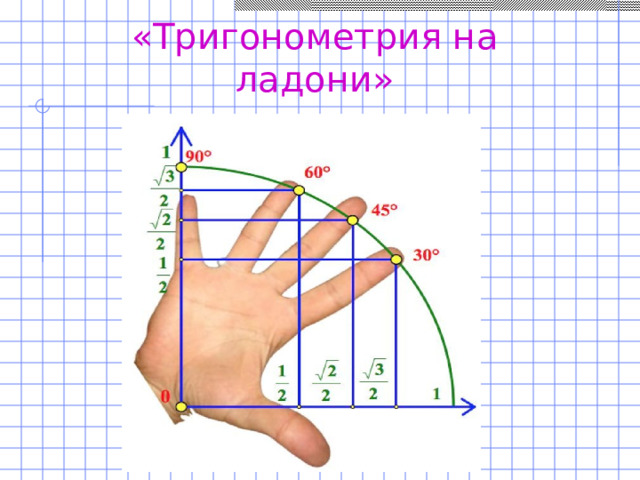
Учащиеся 10 и 11 классов плохо запоминают таблицу точных значений тригонометрических функций. Оказывается, значение синусов и косинусов углов «находятся» на нашей ладони. Этот прием является подспорьем в работе с учащимися.
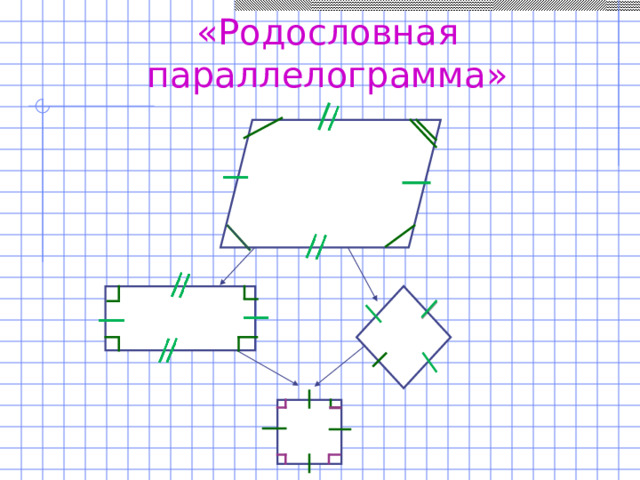
Геометрия очень сложно даётся детям из-за большого объёма теоретического материала который применяется при решении задач. Я заметила что хорошо запоминается материал, когда между вводимыми понятиями, можно установить логические связи, цепочки. Например, при изучении свойств четырехугольников я рисую схему. Параллелограмм – это папа, от него рисуем две стрелки: прямоугольник и ромб, от которых две стрелки сходятся к квадрату. По схеме видно какие свойства передаются «по наследству» и после этого легко сформулировать определения, свойства и признаки четырехугольников.
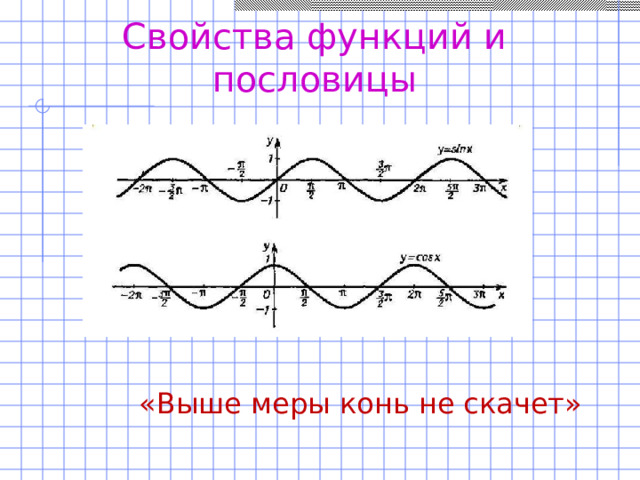
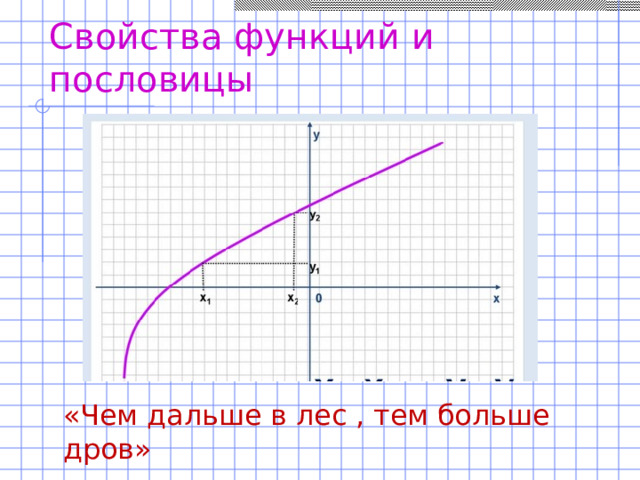
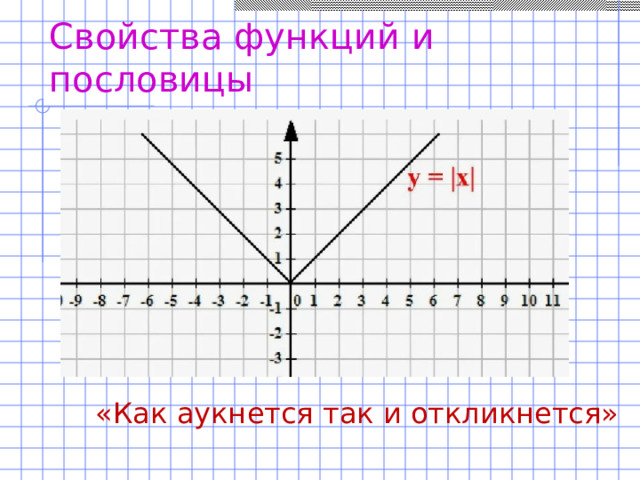
А как украшает урок когда интегрируются две науки математика и литература. Рассматривая свойства функций мы не только строим графики, но в качестве домашнего задания нужно подобрать пословицу соответствующую свойству функции и на уроке это обосновать. И вот что у нас получилось.
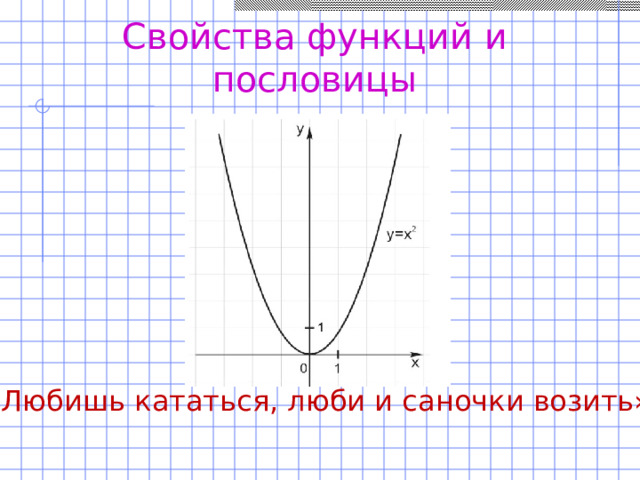
«Выше меры конь не скачет» (область значений синуса и косинуса), «Чем дальше в лес, тем больше дров» (возрастание функции), «Как аукнется, так и откликнется» (график функции у=/х/), «Любишь кататься, люби и саночки возить» (график параболы).
Таким образом, применяя метод ассоциаций, можно помочь обучающимся легче усвоить основные понятия, ход решения, этапы решения каких-то задач.
А в заключение хочу отметить, что медики предлагают гипотезу, что математика продлевает жизнь, давая возможность на долгие годы сохранять ум свежим, а человека работоспособным, энергичным. И моя задача, как учителя – убедить в этом учеников. А каждый выпускник, выходя из стен школы, должен знать, что
“Музыка может возвышать или умиротворять душу,
Живопись – радовать глаз,
Поэзия – пробуждать чувства,
Философия – удовлетворять потребности разума,
Инженерное дело – совершенствовать материальную сторону жизни людей,
А математика способна достичь всех этих целей”.

 Получите свидетельство
Получите свидетельство Вход
Вход







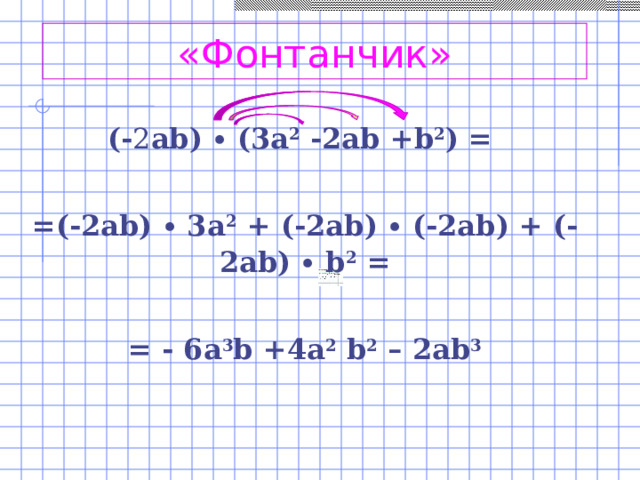












 Простые шаги в сложной математике (1.56 MB)
Простые шаги в сложной математике (1.56 MB)
 0
0 106
106 2
2 Нравится
0
Нравится
0


