Пояснительная записка
к экзаменационному материалу для промежуточной аттестации обучающихся 5 класса по математике
Назначение итоговой контрольной работы.
Итоговая контрольная работа по математике проводится с целью:
Выявить уровень усвоения учащимися курса математики 5 класса для диагностирования математической подготовки и компетентности выпускников 5 классов.
Оценить достижения пятиклассниками базового уровня подготовки, соответствующего Федеральному государственному образовательному стандарту основного общего образования.
Спрогнозировать дальнейшее обучение выпускников 5 класса с внесением корректив в дальнейший процесс обучения.
Документы, определяющие содержание итоговой контрольной работы.
Содержание итоговой контрольной работы соответствует ФГОС ООО, примерной программе и учебникам по математике для 5 класса общеобразовательной школы. Работа содержит элементы содержания «Обязательного минимума содержания основных образовательных программ», которые изучаются в 5 классах.
Структура и содержание итоговой контрольной работы.
Итоговая контрольная работа по математике для 5 классов содержит 13 заданий, проверяющих базовый уровень знаний учащихся на данном этапе. Среди них также имеются более сложные задания. Однако эти задания не требуют знаний каких-либо дополнительных разделов. Они также как и остальные, проверяют уровень владения программным материалом.
В каждом варианте итоговой контрольной работы проверяется уровень подготовки школьников по всем элементам содержания курса математики 5 касса. Соотношение числа заданий по разным элементам содержания опирается на примерную программу по математике и отражает учебное время, отводимое в процессе изучения предмета на тот или иной вопрос темы.
Раздел 1. Перечень элементов содержания, проверяемых на промежуточной (годовой) аттестации по математике.
| Код раздела | Код контролируемого элемента | Элементы содержания |
| 1 |
| Числа и вычисления |
| 1.1 |
| Натуральные числа |
| 1.1.1 | Десятичная система счисления. Римская нумерация | |
| 1.1.2 | Арифметические действия над натуральными числами | |
| 1.1.3 | Степень с натуральным показателем | |
| 1.1.4 | Делимость натуральных чисел. Простые и составные числа, разложение натурального числа на простые множители | |
| 1.1.5 | Признаки делимости на 2, 3, 5, 9, 10 | |
| 1.1.6 | Наибольший общий делитель и наименьшее общее кратное | |
| 1.1.7 | Деление с остатком | |
| 1.2 |
| Дроби |
| 1.2.1 | Обыкновенная дробь, основное свойство дроби. Сравнение дробей | |
| 1.2.2 | Арифметические действия с обыкновенными дробями | |
| 1.2.3 | Нахождение части от целого и целого по его части | |
| 1.3 |
| Рациональные числа |
| 1.3.1 | Числовые выражения, порядок действий в них, использование скобок. Законы арифметических действий | |
| 1.4 |
| Измерения, приближения, оценки |
| 1.4.1 | Единицы измерения длины, площади, объёма, массы, времени, скорости | |
| 1.4.2 | Размеры объектов окружающего мира (от элементарных частиц до Вселенной), длительность процессов в окружающем мире | |
| 1.4.3 | Представление зависимости между величинами в виде формул | |
| 1.4.4 | Прикидка и оценка результатов вычислений. | |
| 2 |
| Уравнения и неравенства |
| 2.1 |
| Уравнения |
| 2.1.1 | Уравнение с одной переменной, корень уравнения | |
| 2.2 |
| Текстовые задачи |
| 2.2.1 | Решение текстовых задач арифметическим способом | |
| 3 |
| Координаты на прямой и плоскости |
| 3.1 |
| Координатная прямая |
| 3.1.1 | Изображение чисел точками координатном луче | |
| 4 |
| Геометрия |
| 4.1 |
| Геометрические фигуры и их свойства. Измерение геометрических величин |
| 4.1.1 | Начальные понятия геометрии | |
| 4.1.2 | Угол. Прямой угол. Острые и тупые углы. | |
| 4.1.3 | Прямая. Параллельность прямых | |
| 4.1.4 | Отрезок | |
| 4.2 |
| Треугольник |
| 4.2.1 | Виды треугольников | |
| 4.3 |
| Многоугольники |
| 4.3.1 | Виды четырехугольников | |
| 4.4 |
| Окружность и круг |
| 4.4.1 | Элементы окружности: радиус, диаметр, хорда, дуга | |
| 4.5 |
| Измерение геометрических величин |
| 4.5.1 | Длина отрезка, длина ломаной, периметр многоугольника. | |
| 4.5.2 | Длина окружности | |
| 4.5.3 | Градусная мера угла | |
| 4.5.4 | Площадь и её свойства. Площадь прямоугольника | |
| 4.5.5 | Формулы объёма прямоугольного параллелепипеда, куба |
Раздел 2. Перечень требований к уровню подготовки, проверяемому на промежуточной (годовой) аттестации
Программа обеспечивает достижение следующих результатов освоения образовательной программы основного общего образования:
формирование представлений о математике как о методе познания действительности, позволяющем описывать и изучать реальные процессы и явления;
развитие умений работать с учебным математическим текстом (анализировать, извлекать необходимую информацию), точно и грамотно выражать свои мысли с применением математической терминологии и символики, проводить логические обоснования;
развитие представлений о числе и числовых системах от натуральных до рациональных чисел; овладение навыками устных, письменных, инструментальных вычислений;
овладение геометрическим языком; развитие умения использовать его для описания предметов окружающего мира; развитие пространственных представлений, изобразительных умений, навыков геометрических построений;
развитие умений применять изученные понятия, результаты, методы для решения задач практического характера с использованием при необходимости справочных материалов, компьютера, пользоваться оценкой и прикидкой при практических расчётах;
умение пользоваться математическими формулами и самостоятельно составлять формулы зависимостей между величинами на основе обобщения частных случаев и эксперимента.
Система оценивания письменных работ
Контрольная работа состоит из двух частей:
заданий базового уровня (из раздела «Ученик научится»);
заданий повышенного (из раздела «Ученик получит возможность научится») уровня.
Соотношение заданий базового и повышенного уровня: 70% и 30% или 60% и 40%.
Шкала перевода баллов в отметку
| Отметка | Количество баллов |
| «2» | Меньше 50% БУ |
| «3» | 50 – 100% БУ |
| «4» | 65 – 100% БУ + 50 – 84% ПУ |
| «5» | 85 – 100% БУ + 85 – 100% ПУ |
Не достиг базового уровня – до 49% БУ
Достиг базового уровня – от 50% БУ
Достиг повышенного уровня – 65% БУ + 50% ПУ
Достиг высокого уровня – 85% БУ + 85% ПУ
| № задания | Уровень сложности | Макс. балл | |
| 1 | Б | 1 | |
| 2 | Б | 2 | |
| 3 | Б | 2 | |
| 4 | Б | 2 | |
| 5 | Б | 2 | |
| 6 | Б | 1 | |
| 7 | Б | 1 | |
| 8 | Б | 1 | |
| 9 | Б | 1 | |
| 10 | Б | 1 | |
| 11 | П | 5 | |
| 12 | П | 4 | |
| 13 | П | 4 | |
| Базовый уровень | 14 | ||
| Повышенный уровень | 13 | ||
| Итого: | 27 | ||
| Отметка | Количество баллов |
| «2» | 0 – 7 |
| «3» | 8 – 15 |
| «4» | 16 – 22 |
| «5» | 23 – 27 |
Промежуточная аттестация по математике за курс 5 класса в 2017-2018уч.г.
Ф.И. учащегося
Вариант 1
Часть 1
1) Разложите на простые множители число 650.
2) Вычислите 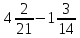 .
.
3) Вычислите 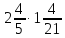 .
.
4) Вычислить: 2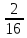 : 1
: 1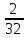 .
.
5) Вычислите 42+73.
6) Найдите площадь прямоугольника, ширина которого 6 м, а длина на 3 м больше.
7) Найдите 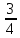 числа 60.
числа 60.
8) Найдите число, 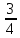 которого равны 60.
которого равны 60.
9) Собственная скорость лодки 10 км/ч, а скорость течения реки 2 км/ч. За сколько часов лодка проплывёт 24 км по течению?
10) Найти периметр прямоугольника, если его стороны равны 3 дм и 11 дм.
Часть 2
11) Вычислить: (33:30 - 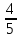 )*2
)*2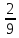 +
+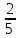
12) На координатном луче отметьте точки О(0), В(7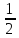 ) и точку С так, чтобы расстояние ВС было равно 3. Укажите все возможные решения задачи.
) и точку С так, чтобы расстояние ВС было равно 3. Укажите все возможные решения задачи.
13) Первая бригада может выполнить задание за 12 дней, а вторая – за 60 дней. За сколько дней могут выполнить это задание две бригады при совместной работе?
Промежуточная аттестация по математике за курс 5 класса в 2017-2018уч.г.
Ф.И. учащегося
Вариант 2
Часть 1
1) Разложите на простые множители число 620.
2) Вычислите 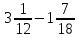 .
.
3) Вычислите 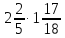 .
.
4) Вычислить: 2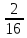 : 1
: 1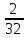 .
.
5) Вычислите 52+63..
6) Найдите площадь прямоугольника, ширина которого 4 дм, а длина на 5 дм больше.
7) Найдите 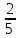 числа 40.
числа 40.
8) Найдите число, 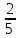 которого равны 40.
которого равны 40.
9) Собственная скорость лодки 8 км/ч, а скорость течения реки 2 км/ч. За сколько часов лодка проплывёт 30 км по течению?
10) Найти периметр прямоугольника, если его стороны равны 5 см и 9 см.
Часть 2
11) Вычислить: (33:30 - 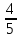 )*2
)*2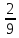 +
+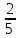
12) На координатном луче отметьте точки О(0), В(6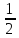 ) и точку С так, чтобы расстояние ВС было равно 4. Укажите все возможные решения задачи.
) и точку С так, чтобы расстояние ВС было равно 4. Укажите все возможные решения задачи.
13) Первая бригада может выполнить задание за 20 дней, а вторая – за 60 дней. За сколько дней могут выполнить это задание две бригады при совместной работе?

 Получите свидетельство
Получите свидетельство Вход
Вход












 Промежуточная аттестация по математике 5 класс (26.07 KB)
Промежуточная аттестация по математике 5 класс (26.07 KB)
 0
0 6148
6148 361
361 Нравится
0
Нравится
0


