«Производная, всемогущая».
Здравствуйте ребята, садитесь! У нас сегодня на уроке гости, давайте, друзья, улыбнемся друг другу, улыбки подарим гостям.
У вас все готово? Тогда за работу.
Ребята, если вы правильно отгадаете ключевое слово, то узнаете тему нашего урок.
С ее появлением математика перешагнула из алгебры в математический анализ;
Имеет физический и геометрический смысл;
бывает первой, второй,…;
Обозначается штрихом.
1 слайд: Молодцы, тема нашего занятия «Производная, всемогущая».
Как вы думаете, ребята, какова цель нашего урока? (дети формулируют цель)
Цель нашего урока – повторить основные направления применения производной для решения различных задач дифференциального исчисления.
Я желаю вам на уроке удачи, точных расчетов и вычислений.
Активизация знаний учащихся. На одном из первых уроков изучения производной вы мне задали вопрос:
Мы изучаем производную, а так ли это важно в жизни? Применяется ли производная в различных областях науки?
Постараемся, ответит на этот вопрос сегодня на уроке.
2 слайд: А чтобы у вас была путеводная звезда, к которой бы вы шли, я выдвинула гипотезу «Дифференциальное исчисление – это описание окружающего нас мира, выполненное на математическом языке. Производная помогает нам успешно решать не только математические задачи, но и задачи практического характера в разных областях науки и техники».
В ходе урока вы подтвердите или опровергните эту гипотезу.
3 слайд: 2. У вас на столах лежат оценочные листы. За каждый правильный ответ, выполненное задание вы будете начислять себе по одному баллу.
| № | Этап урока | Баллы |
| | Разминка |
|
| | Найди соответствие |
|
| | Значение производной в точке |
|
| | Геометрический смысл производной |
|
| | Физический смысл производной |
|
| | Работа исследователей |
|
| | Свойства функций и свойства производной |
|
|
| Средний балл: |
|
|
| Оценка : |
|
Приятно, что к соревнованию человек готовится, и свой день обычно начинает с зарядки, т.е. с разминки. Проведем разминку перед практической частью и мы.
4 слайд: Для этого возьмем кроссворд, который вам нужно было разгадать дома.
По горизонтали: 2 мин
1.Как называется число, к которому стремится отношение приращения функции к соответствующему приращению аргумента, при стремлении приращения аргумента к нулю…(производной)
4.Точки области определения, в которых производная функции не существует, называются ….точками. (критическими)
5.Точки максимума и минимума называют точками… (экстремума)
7.Промежутки возрастания(убывания) функции это промежутки… (монотонности)
По вертикали:
2.Процесс изучения какого-либо объекта, например, функции? (исследование)
3. Какой смысл производной заключается в том, что скорость движения материальной точки в данный момент времени равна производной пути по времени? (механический)
6. Производная чего равна нулю? (константы)
5 слайд: Ставим баллы за правильно выполненное задание.
Прежде чем приступить к повторению основных направлений применения производной, проверим нашу готовность к вычислению производных.
6 слайд: 3.Найди соответствие 3 мин
Укажите соответствие между функцией и ее производной: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца.
Под каждой буквой укажите номер ее возможного значения.
| № | Функция |
| Производная |
| А | k | 1 | nxn-1 |
| Б | хn | 2 | 0 |
| В | √х | 3 | 1/2√x |
| Г | sin x | 4 | -1/x2 |
| Д | cos x | 5 | sin x |
| Е | tg x | 6 | cos x |
| Ж | 1/x | 7 | 1/ cos2x |
Проверяем: 2136574. Ставим баллы в оценочные листы.
Мы освоили приемы нахождения простейших производных суммы, разности, произведения и частного элементарных функций. Сейчас постараемся применить полученные знания при решении задач.
7 слайд: 4.Значение производной в точке. 7 мин
Предлагаю, вам задание, выполнив которое вы узнаете, как Ньютон называл производную функции.
| С | у = х2 + 2х3 | у′(1) - ? |
| Я | у = 2 cos x | у′(-п/3) - ? |
| Ю | у = (2 + 6х)2 | у′(1/6) - ? |
| Ф | у = √х | у′(4) - ? |
| К | у = (х-3) (2х + 5) | у′(1) - ? |
| И | у =3 – sin2x | у′(п/2) - ? |
| Л | у = 24ln(х+4) | у′(-2) - ? |
| 1/4 | -12 | 36 | 3 | 8 | 2 | √3 |
|
|
|
|
|
|
|
|
Ставим баллы в оценочные листы.
8 слайд: 6.Геометричексий смысл производной. 3 мин
Предлагаю работу по вариантам (по 1 к доске)
1 вариант: Найдите тангенс угла наклона касательной к графику функции S (t) = t3 – t2 в точке t = 3 .
2 вариант: Найти угловой коэффициент касательной к графику функции у = f (x) в точке с абсциссой х0. f (x) = cos3x, х0 = π/6
Какие знания вы применяли при выполнении данных заданий? В чем заключается геометрический смысл производной?
9-12 слайд: Теперь поработаем с графиками: 3 мин
а) на рисунке изображен график функции у = f (x) и касательная к этому графику, проведенная в точке с абсциссой х0. Найдите значение производной функции f (x) в точке х0.
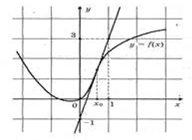
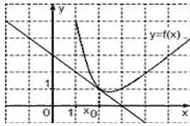
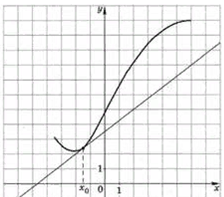
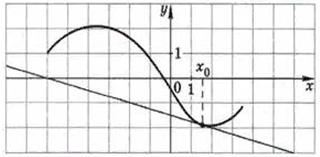
13 слайд: 7.Физический смысл производной. 3 мин
Материальная точка движется прямолинейно по закону S(t) = 6t2 – 48t + 17, где S(t) – расстояние от точки отсчета в метрах, t – время в секундах, измеренное с начала движения. Найдите ее скорость в момент времени t = 9 с.
Что вам необходимо знать о производной, чтобы решить данную задачу?
(желающий решает у доски).
Давайте вспомним, что характеризует производная в физике?
(В физике производная характеризует скорость прямолинейного движения).
8.Применение знаний и умений в новой ситуации. 15 мин
А в каких науках вы можете еще встретить задачи на скорость?
Ученик: на уроке химии – скорость химической реакции.
Вопрос: какое определение в химии вы даете скорости химической реакции? И как это записать?
Ученики: скоростью химической реакции называется изменение концентрации, реагирующий веществ, в единицу времени. Записывается ѵ(t ) = ∆С/∆ t.
На языке математике концентрация – это функция, а время – аргумент. Скорость химической реакции равна производной концентрации вещества, вступившего в реакцию ѵ(t ) = С′ (t) .
Какой вывод можно сделать? Мы с вами вывели химический смысл производной, теперь решая химические задачи на нахождение скорости химической реакции, вы можете использовать производную.
14 слайд: Давайте попробуем решить задачу:
Пусть количество вещества, вступившего в реакцию, задается зависимостью
С (t) = t2/2 +3t – 3. Найти скорость химической реакции через 3 секунды.
С точки зрения химиков важно изучать скорость химической реакции?
Ученики: скорость химической реакции – важна химикам, разрабатывающим препараты для медицины и сельского хозяйства, а также врачам и агрономам, использующим эти препараты для лечения людей и для внесения их в почву. Одни реакции проходят практически мгновенно, другие идут очень медленно.
Применяется ли производная в других областях науки? На этот вопрос помогут ответить три исследователя, которые работали дома по применению производной в различных отраслях науки.
Биологический смысл производной. (Буланова Е.)
Биологический смысл производной связан с популяциями. Популяция – это совокупность особей данного вида, занимающих определённый участок территории внутри ареала вида, свободно скрещивающихся между собой.
Если зависимость между числом особей популяции микроорганизмов и временем её размножения задана уравнением: у = x(t), тогда отношение изменение числа особей организмов к промежутку времени, за которое произошло это изменение равна ∆у/∆t, а это является средней скоростью размножения или, как принято говорить, средней производительностью жизнедеятельности популяции.
На языке математики популяция микроорганизмов - это функция, а время – аргумент.
Вывод: значит, скорость роста популяции есть производная численности популяции в момент времени t.
Задача: Пусть зависимость между числом особей популяции микроорганизмов и временем её размножения задана уравнением: х(t) = 3000 + 100t2. Найти скорость роста популяции в момент времени t = 1 с.
Географический смысл производной (Рогожин И.)
Географический смысл производной заключается в росте численности населения.
Для того, чтобы вычислить численность населения на ограниченной
территории в момент времени t поступим следующим образом.
Пусть у = у(t)- численность населения.
Прирост населения за промежуток время ∆t будет находиться по формуле:
∆y = k •∆t, где коэффициент прироста к = кр – кс (кр – коэффициент рождаемости, кс – коэффициент смертности). Выразив к из данной формулы, получим, что k =∆y/∆t
На языке математики рост численности населения - это функция, а время – аргумент.
Вывод: Рост численности населения равен производной численности населения в момент времени t.
3)Экономический смысл производной. (Ерышева Кс.)
Экономический смысл производной связан с производительностью труда. Производительность труда измеряется количеством продукции, выпущенной работником за какое-то время. В экономике очень часто объем произведенной продукции задается формулой. Например, пусть объем продукции выпущенной в течение дня задан формулой у = -2t3 +10t2 +50t – 16, где t – время, выраженное в часах. Для нахождения производительности труда в определенный промежуток времени t0, необходимо найти предельное среднее значение средней производительности за период времени Δt, т. е. у´(х).
На языке математике производительность - функция, время – аргумент.
Вывод производительность труда есть производная объема выпускаемой продукции.
Задача: Вычислить производительность труда во время пяти часов работы, при условии, что объем продукции в течение рабочего дня представлен функцией:
у = -2t3 +10t2 +50t – 16
Вывод: После второго часа работы производительность работы начинает падать. Такой результат является следствием усталости, ухудшением условий в помещении и много других факторов, влияющих на производительность труда. Можно сделать вывод, что продуктивными являются первые два часа работы.
15 слайд: Учитель: Предлагаю вам в качестве домашнего задания задачи на вычисления производительности труда во время первых 4 часов работы.
Сделайте вывод «производная, всемогущая?»
Производная помогает нам успешно решать не только математические задачи, но и задачи практического характера в разных областях науки и техники.
16-17 слайд: 9. Теперь повторим свойства функций и свойства производных.
4 мин
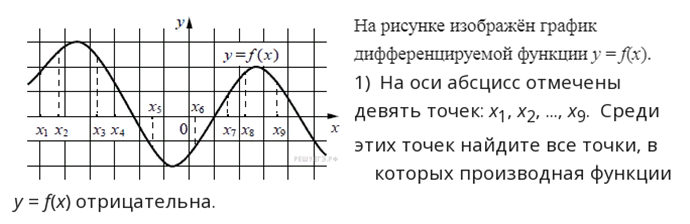
На рисунке изображен график дифференцируемой функции у = f(х). На оси абсцисс отмечены девять точек: х1, х2,х3,…, х9. Среди этих точек найдите все точки, в которых производная функции у = f(х) отрицательна.
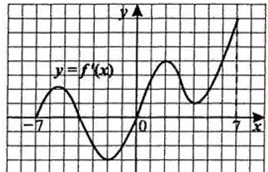
По графику производной функции ответьте на вопросы:
Сколько точек максимума имеет эта функция?
Назовите точки минимума?
Сколько промежутков возрастания у этой функции?
Найдите длину промежутка убывания этой функции?
Подведение итогов урока. Выставление оценок.
Вы замечательно поработали. Надеюсь, этот материал вы не забудете, он пригодится вам на ЕГЭ.
Как вам кажется, достигнуты ли цели урока?
Что удалось?
Что вам показалось наиболее интересным?
Может что-то не получилось?
Понравился вам урок?
Вернемся к оценочным листам. Те, кто набрал от 7 до 8 баллов получают оценку отлично, 6 баллов – 4. ДЗ вы получили.
Молодцы! Я хочу пожелать, чтобы у вас была только положительная производная, чтобы знания ваши только возрастали.

 Получите свидетельство
Получите свидетельство Вход
Вход











 Производная всемогущая (295.42 KB)
Производная всемогущая (295.42 KB)
 0
0 126
126 3
3 Нравится
0
Нравится
0


