Проектная работа

ПРОЕКТНАЯ РАБОТА

по направлению «Математика»

ТЕМА: «Площади плоских фигур»

г. Сургут, 2022 г.

Паспорт проекта

Тема: Площади плоских фигур.

Вид: индивидуальный проект.

Актуальность: геометрические задачи на нахождение площади плоских фигур довольно таки часто встречается в жизни и в заданиях основного государственного экзамена по математике.

Цель: изучение различных формул нахождения площадей плоских фигур.

Задачи:

1. Изучить необходимую литературу.

2. Рассмотреть плоские фигуры.

3. Изучить формулы нахождение площадей.

4. Сделать памятку по данной теме.

Объект исследования: плоские фигуры.

Предмет исследования: площади плоских фигур.

Методы работы: анализ и синтез информации.

Отзыв на итоговый индивидуальный проект

обучающейся 9Е класса МБОУ «СОШ № 29»

Киселёвой Екатерины Олеговны,

по теме «Площади плоских фигур»

Представленный на рецензию итоговый индивидуальный проект представляет собой исследование по изучению формул нахождения площадей плоских фигур. Актуальность работы заключается в том, что она встречается в заданиях основного государственного экзамена.

Цель исследования: изучение различных формул нахождения площадей плоских фигур. В ходе работы решались следующие задачи:

1. Изучить необходимую литературу.

2. Рассмотреть плоские фигуры.

3. Изучить формулы нахождение площадей.

4. Сделать памятку по данной теме.

Содержание работы соответствует заявленной теме. Текст работы изложен на 12 страниц, что представляется достаточным для обучающегося 9 класса.

Работа включает в себя введение, основную часть из двух глав, заключение, список источников информации и приложения. Во введении указывается актуальность исследования, ставятся цель и задачи.

В первой главе прописаны теоретические основы по данной теме. Во второй главе описываются формулы нахождения площади плоских фигур. Завершается работа выводами, в которых излагаются результаты исследования.

Работу Екатерина выполняла самостоятельно, используя материалы Интернета и литературы, рекомендованной её для исследования. Формулировки задач отвечают поставленной цели. Соблюдена этика цитирования, грамотное использование источников. При выполнении работы проявила самостоятельность, творчество, инициативу, способность решать соответствующие исследовательские проблемы. Следует отметить сформированность у обучающейся метапредметных УУД: регулятивных действий, коммуникативных навыков, сформированность ИКТ-компетентности. Киселёва Екатерина чётко выполняла все рекомендации научного руководителя и вовремя устраняла замечания в процессе доработки проектной работы.

Рекомендации: итоговый индивидуальный проект Киселёвой Екатерины по теме:

«Площади плоских фигур» отвечает требованиям, предъявляемым к индивидуальным проектам, и рекомендуется к защите.

Дата Подпись руководителя

Глава I. Многоугольник 4

1.1. Понятие площади 4

1.2. Свойства площадей 4

Глава II. Площади плоских фигур. 5

2.1. Треугольник 5

2.2. Параллелограмм 6

2.3. Квадрат. 7

2.4. Прямоугольник. 7

2.5. Ромб 7

2.6. Трапеция 7

2.7. Круг 8

Заключение 10

Список литературы 11

Приложение 12

Введение.

«Я думаю, что никогда до настоящего времени мы не жили в такой геометрический период. Всё вокруг – геометрия».

Ле Корбюзье

Мир, который нас окружает, наполнен геометрией домов и улиц, гор и полей, творениями природы и человека. Для наилучшего ориентирования в нём, открытия нового, понимания красоты и мудрости окружающего нас мира помогает геометрия.

В жизни мы очень часто встречаемся с понятием “площадь”. С формулами нахождения площадей плоских фигур прямоугольника, квадрата, треугольника, параллелограмма и круга мы знакомимся в школьном курсе. На вычисление площадей четырёхугольников, треугольников обращается особое внимание, так как нам всем необходимо сдавать Основной Государственный и Единый Государственный экзамены по математике, где есть задачи для определения площади многоугольника. Но встречаются и такие задания, в которых необходимо найти площади фигур, которые на уроках не рассматриваются. Поэтому я решила рассмотреть и систематизировать формулы нахождения площадей плоских фигур.

Цель: изучение различных формул нахождения площадей плоских фигур.

Задачи:

1. Изучить необходимую литературу.

2. Рассмотреть плоские фигуры.

3. Изучить формулы нахождение площадей.

4. Сделать памятку по данной теме.

Объект исследования: плоские фигуры.

Предмет исследования: площади плоских фигур.

Методы работы: анализ и синтез информации.

Многоугольник – это геометрическая фигура, ограниченная замкнутой ломаной линией, состоящая из трех и более отрезков.

Выпуклый многоугольник, у которого все углы равны и все стороны равны называется правильным многоугольником.

Многоугольник называется выпуклым, если он лежит по одну сторону от каждой прямой, проходящей через две его соседние вершины.

Измерение площадей является одним из самых древних разделов геометрии. В частности, название “геометрия” означает “землемерие”, т.е. связано именно с измерением площадей. В Древнем Египте были заложены основы этой науки, так как после каждого разлива Нила приходилось заново производить разметку участков, покрытых плодоносным илом – вычислять их площади. Многие ученые работали над проблемой вычисления площадей фигур. Благодаря им были выведены формулы, применяя которые можно вычислить площади прямоугольника, треугольника, трапеции. Эти формулы нужны не только в геометрии, но и в практической деятельности.

Площадь многоугольника – это величина той части плоскости, которую занимает многоугольник.

Если два многоугольника равны, то единица измерения площадей и её части укладываются в таких многоугольниках одинаковое число раз, т.е. имеет место следующее свойство:

1⁰. Площадь каждого многоугольника – положительное число.

2⁰. Равные многоугольники имеют равные площади.

3⁰. Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников.

4⁰. Площадь квадрата со стороной, равной единице длины, равна одной единице измерения.

Глава II. Площади плоских фигур.

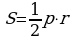– правильного многоугольника, где p – периметр правильного многоугольника, r – радиус вписанной окружности.

2.1. Треугольник

Треугольник - это геометрическая фигура, состоящая из трех отрезков, которые соединяют три точки, не лежащие на одной прямой.

Медиана треугольника ― отрезок, соединяющий вершину треугольника с серединой противоположной стороны

Биссектриса угла — луч, исходящий из вершины угла и делящий этот угол на два равных угла.

Высота треугольника — перпендикуляр, опущенный из вершины треугольника на противоположную сторону (точнее, на прямую, содержащую противоположную сторону).

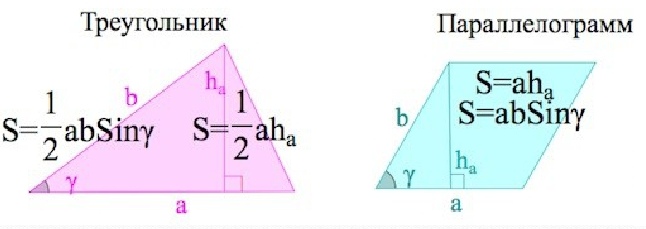
Чтобы найти площадь треугольника нужно чтобы была известна хотя бы одна сторона треугольника и высота, проведенная к ней. В этом случае поможет классическая формула

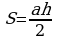, где a - длина стороны треугольника, принятой за основание, h – длина высоты треугольника. Важно выбрать ту высоту, которая опущена именно к основанию.

Если известны две стороны треугольника и угол между ними. Работает формула 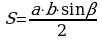, где a, b – известные длины сторон треугольника, β – величина угла между ними.

Если известны все три стороны треугольника. Здесь поможет формула Герона S=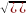 , где a, b, c – стороны треугольника, p – полупериметр. Чтобы найти полупериметр, надо сложить длины всех сторон треугольника и разделить сумму пополам.

Ч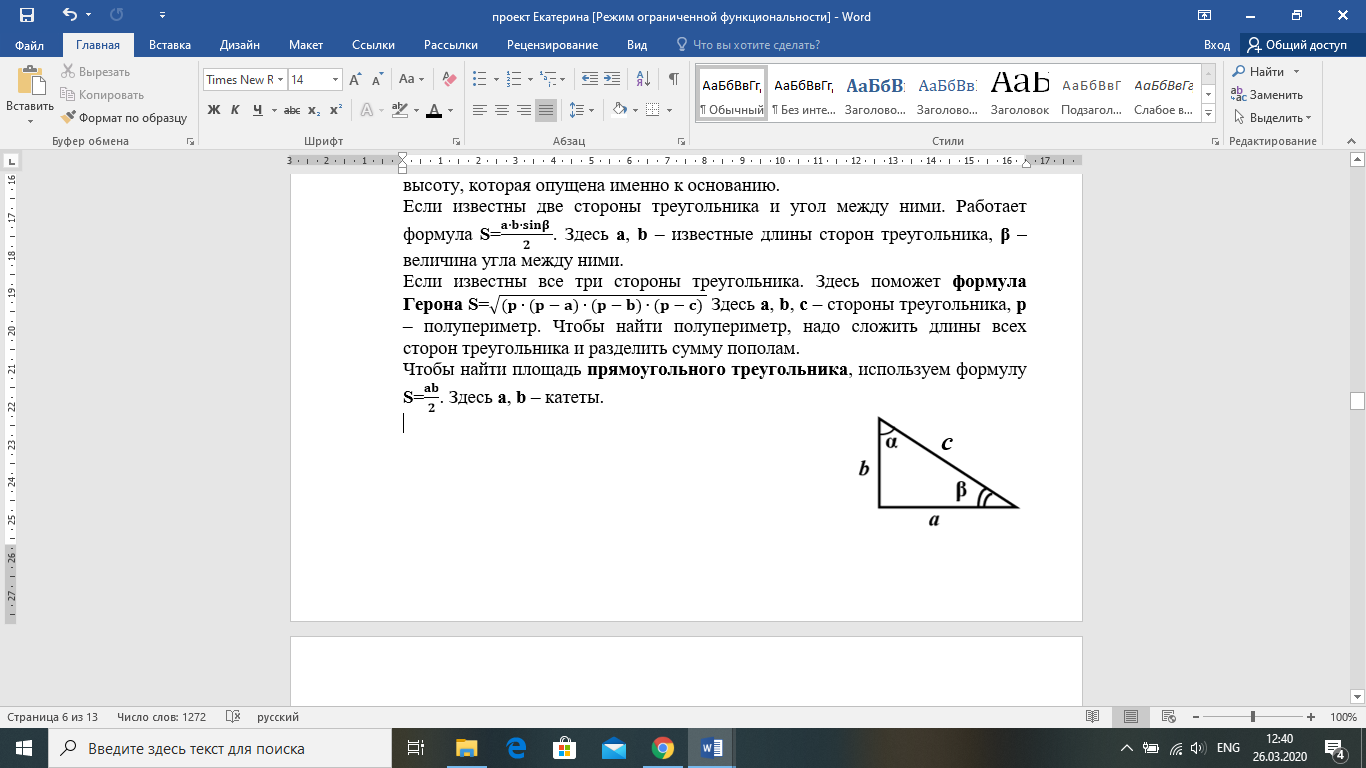 тобы найти площадь прямоугольного треугольника, используем формулу 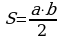, где a, b – катеты треугольника.

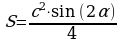, где с – гипотенуза треугольника, β – острый угол.

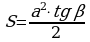, где a – катет треугольника, β – острый угол, прилежащий к катету а.

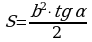, где b – катет треугольника, α – острый угол, прилежащий к катету b.

Параллелограмм — это четырехугольник, у которого противоположные стороны параллельны, то есть лежат на параллельных прямых.

Площадь параллелограмма можно найти по формулам:

1) 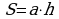, где а – сторона параллелограмма, h – высота, проведенная к этой стороне.

2) 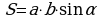, где а, b – стороны параллелограмма, 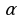– угол между этими сторонами.

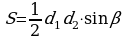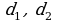3) , где – диагонали параллелограмма, 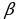– угол между этими диагоналями.

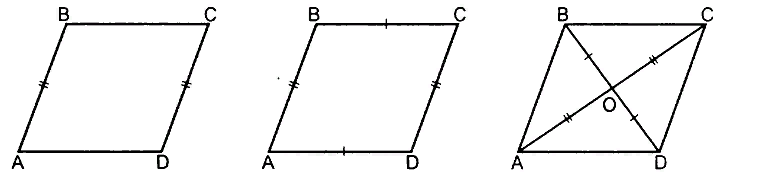
Квадрат - правильный четырёхугольник, у которого все стороны и углы равны между собой. У квадрата есть две диагонали, соединяющие несмежные вершины.

Формулы нахождение площади квадрата:

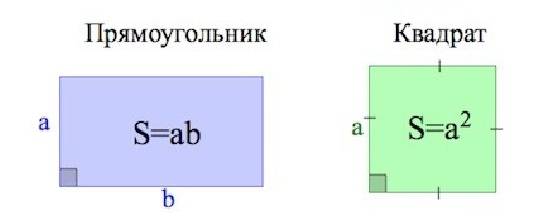
1) 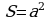, где а – сторона квадрата.

2) 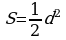, где d – диагональ квадрата.

Прямоугольник – это параллелограмм, у которого все углы прямые.

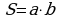
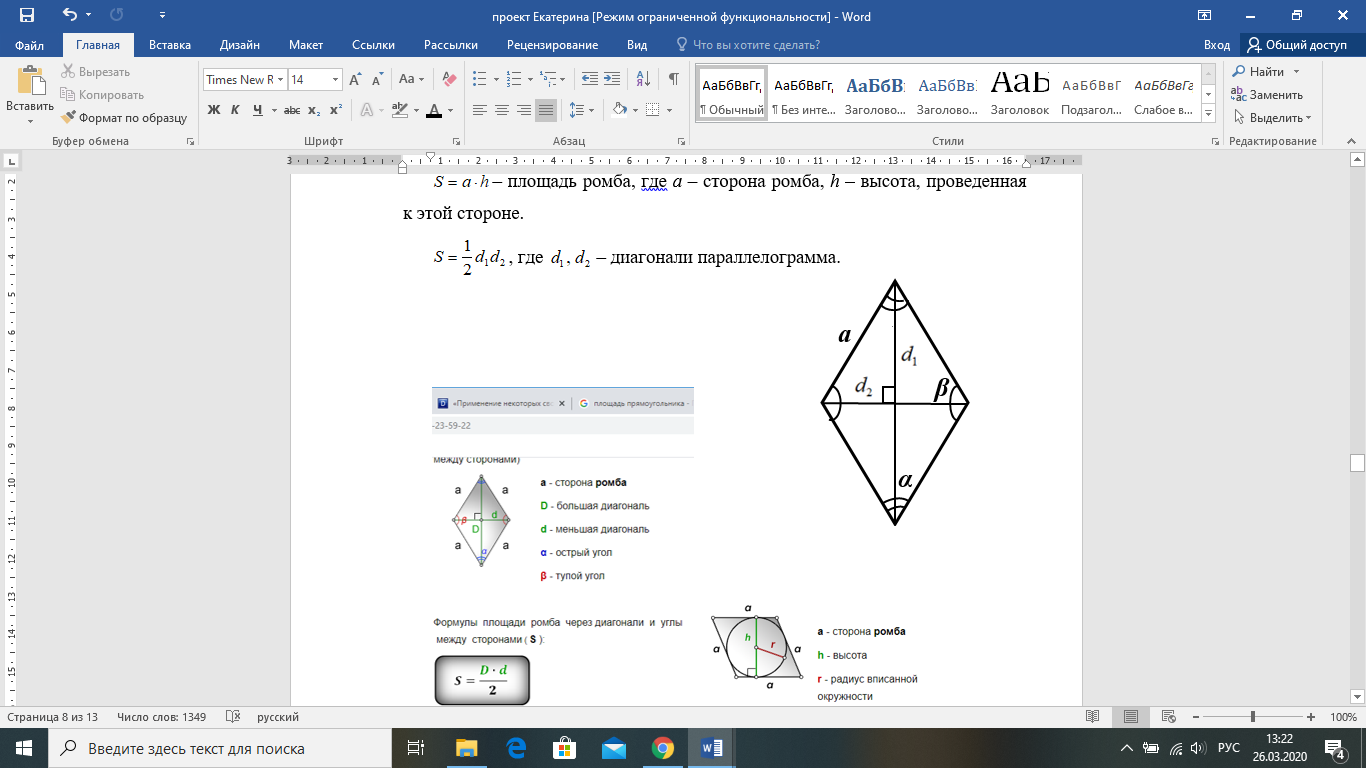, где a – длина прямоугольника, b – ширина прямоугольника.

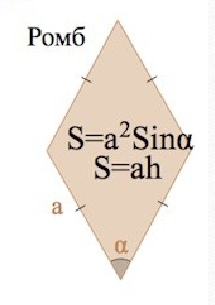
Ромб – это параллелограмм, у которого все стороны равны.

Диагонали ромба взаимно перпендикулярны, точкой пересечения делятся пополам, являются биссектрисами углов.

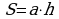
– площадь ромба, где а – сторона ромба, h – высота, проведенная к этой стороне.

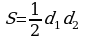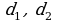, где – диагонали параллелограмма.

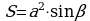, где a – сторона ромба, 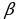– угол между сторонами.

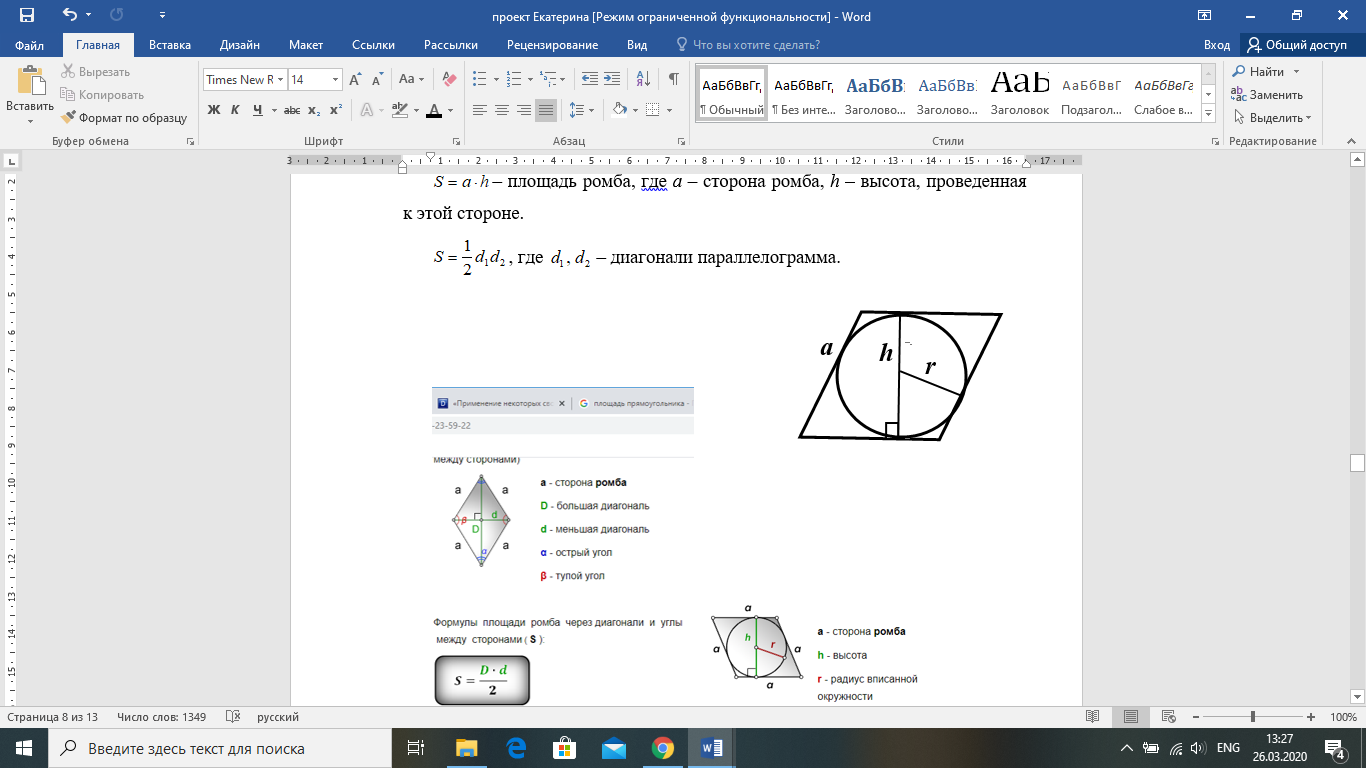
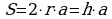, где a – сторона ромба, r – радиус вписанной окружности, h – высота ромба.

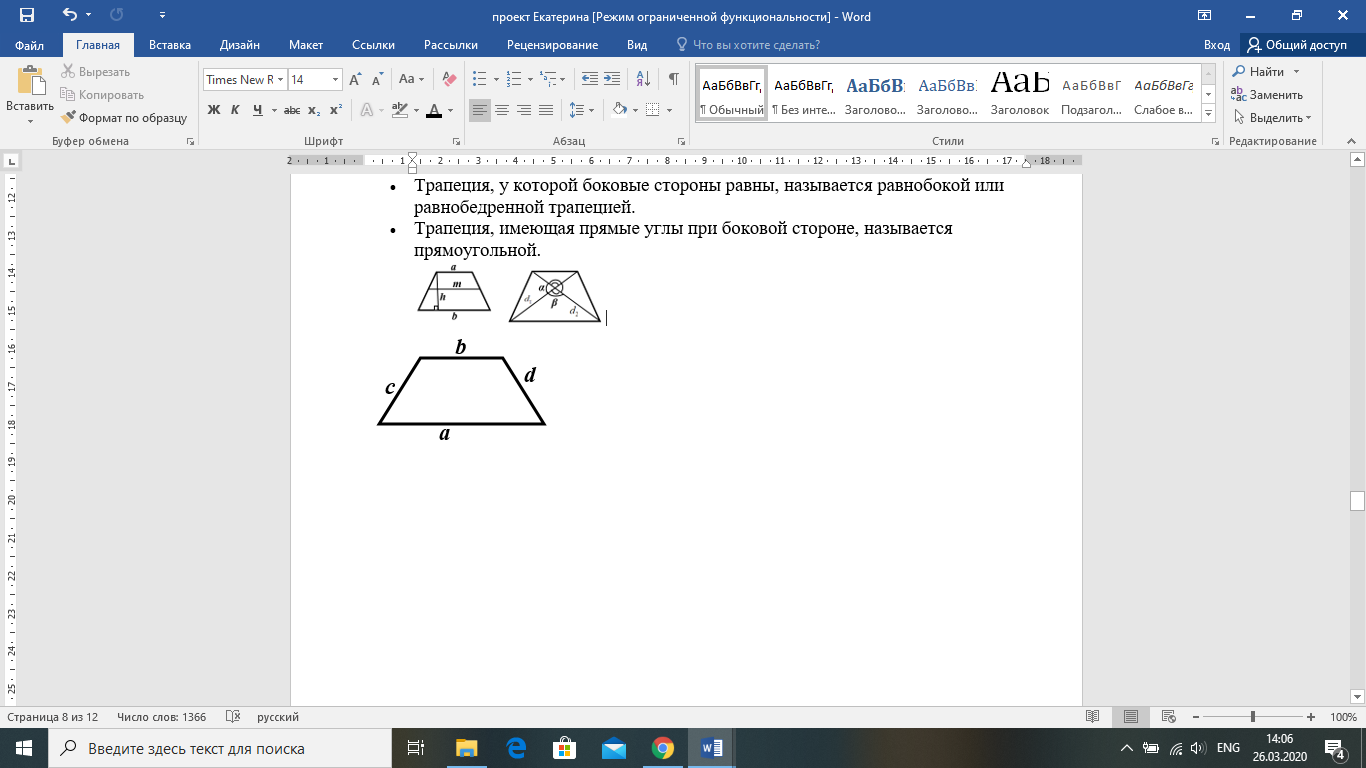
Трапеция — выпуклый четырёхугольник, у которого две стороны параллельны, а две другие не параллельны. Основаниями трапеции называются стороны противоположные и параллельные, а боковыми две другие стороны. Средняя линия трапеции — отрезок, соединяющий середины боковых сторон.

Виды трапеций

• Трапеция, у которой боковые стороны равны, называется равнобокой или равнобедренной трапецией.

• Трапеция, имеющая прямые углы при боковой стороне, называется прямоугольной.

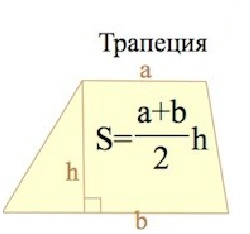
П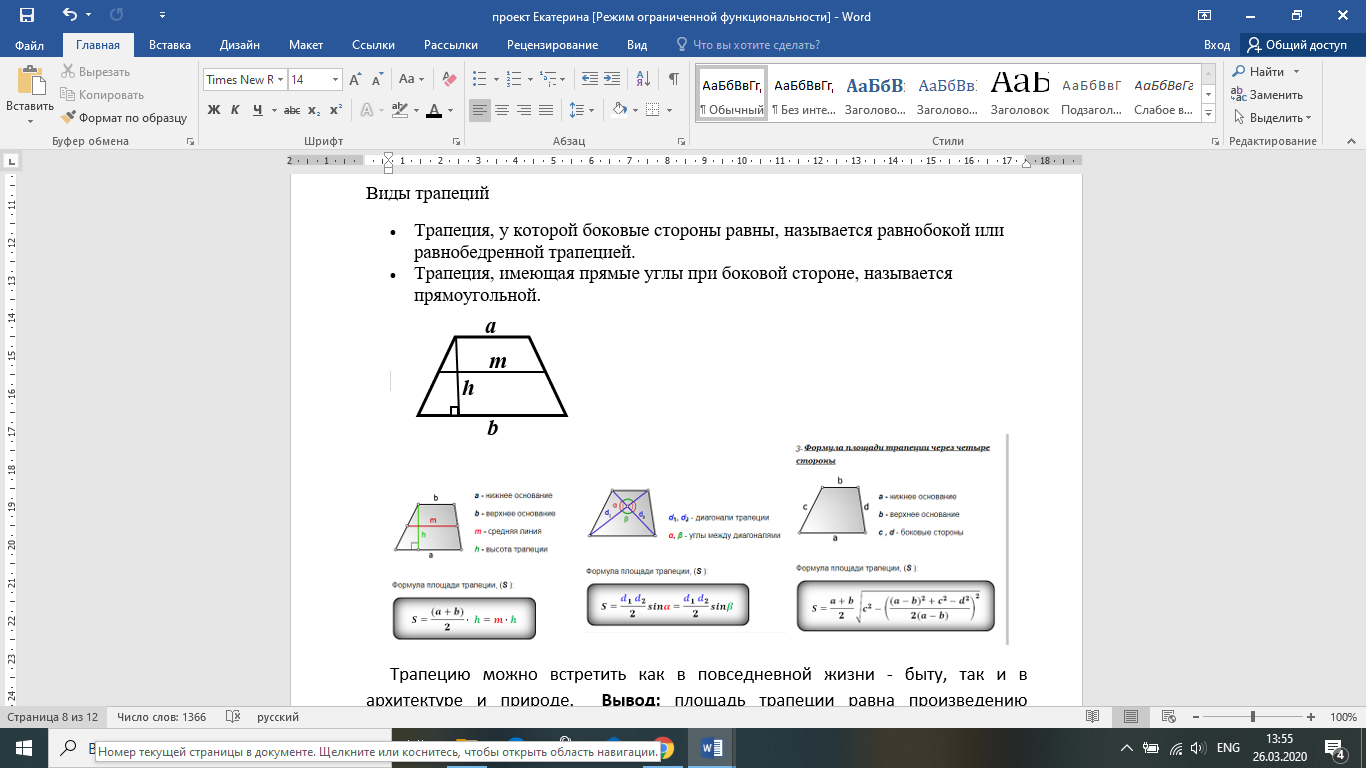 лощадь трапеции равна произведению полусуммы оснований на высоту трапеции.

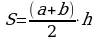, где a, b – основания трапеции, h – высота трапеции.

П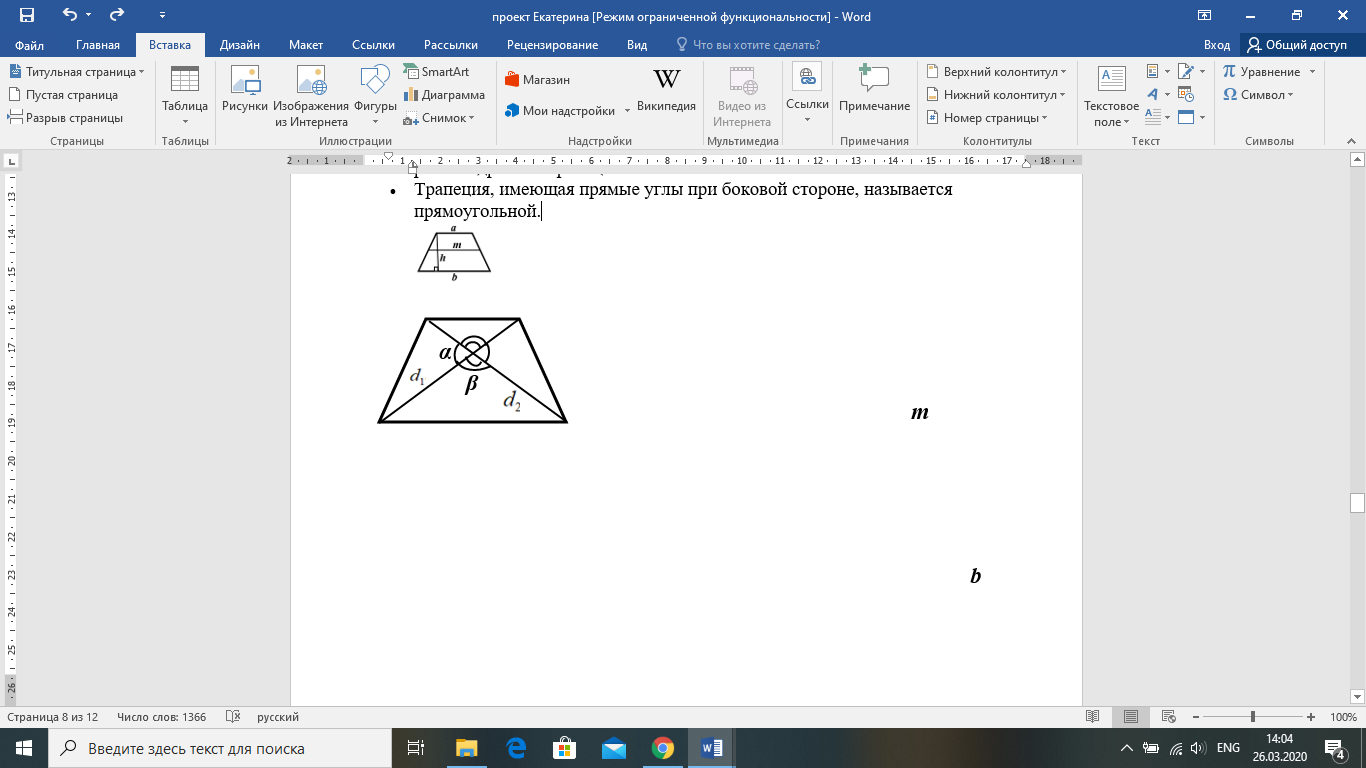 лощадь трапеции равна произведению средней линии на высоту трапеции. 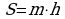, где h – высота трапеции, m – средняя линия трапеции.

Площадь трапеции равна произведению диагоналей трапеции на синус угла между ними деленному на 2.

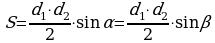
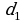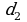, где , – диагонали трапеции, 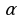, 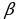– угол между диагоналями.

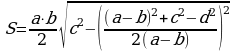, где а, b – основания трапеции, с, d – боковые стороны.

2.7. Круг

Круг – это часть плоскости, все точки которой, расположены на любом расстоянии от определенной точки (центр круга) но не больше заданной длины (радиус).

Чтобы найти площадь круга, нужно знать только его радиус. Но нужно уметь преобразовывать другие исходные величины, чтобы воспользоваться этой формулой.

S=πr² – площадь круга, где π ≈ 3,14, r – радиус круга.

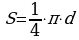, где d – диаметр круга.

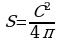
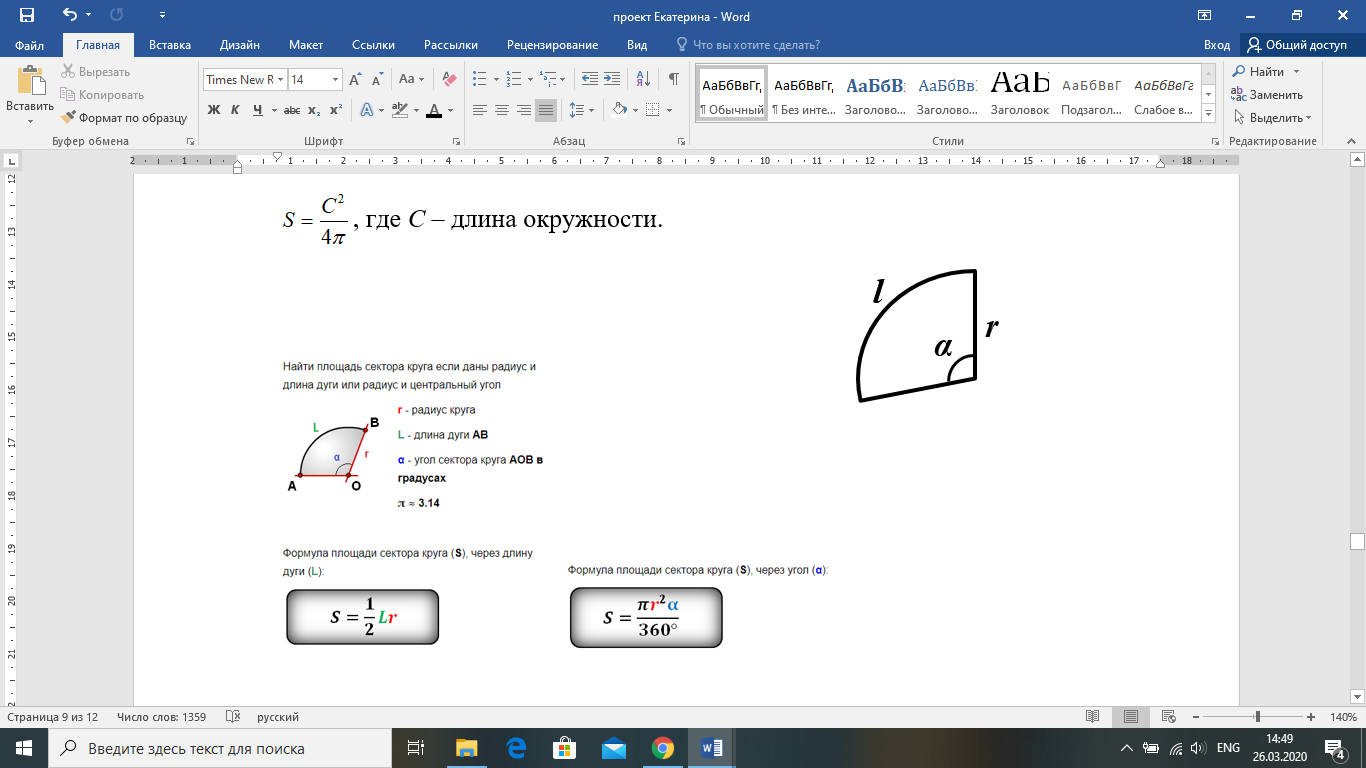, где С – длина окружности.

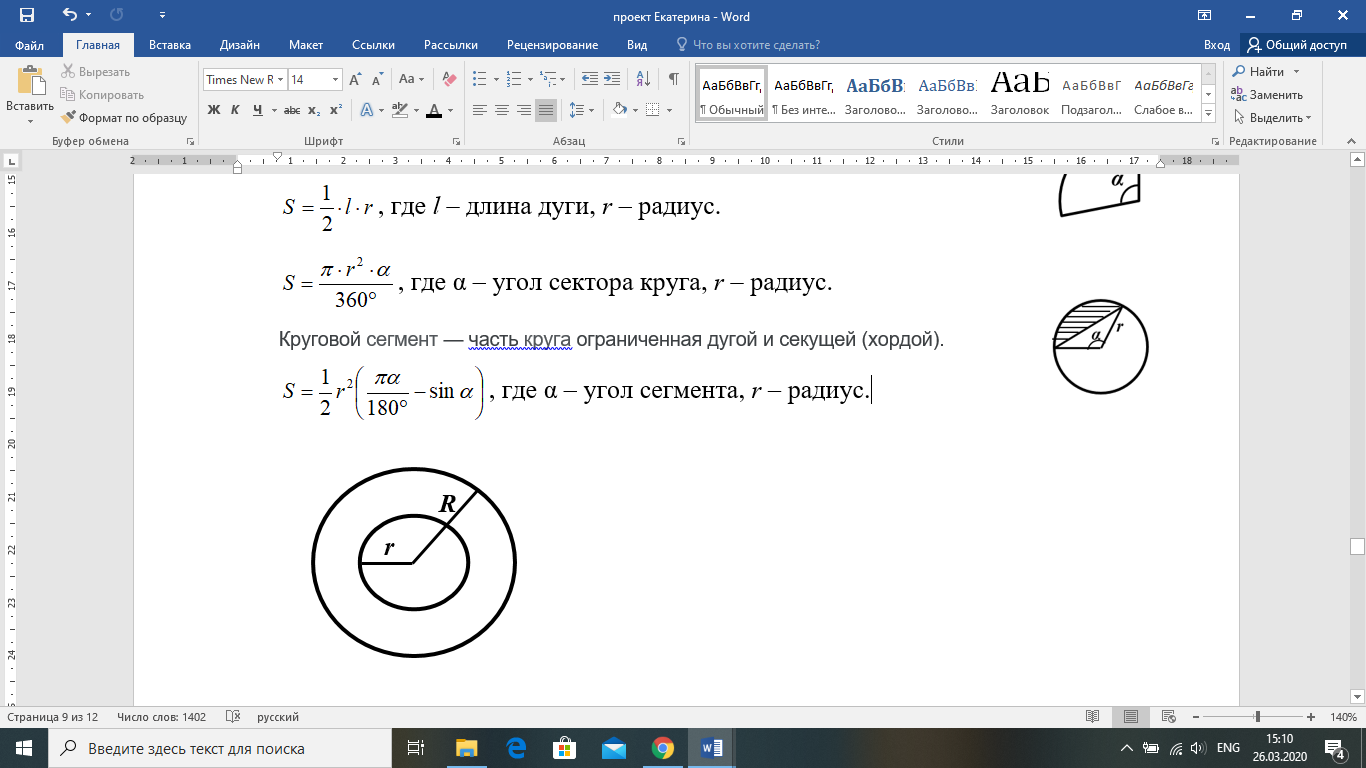
Сектор круга — часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.

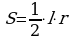, где l – длина дуги, r – радиус.

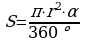
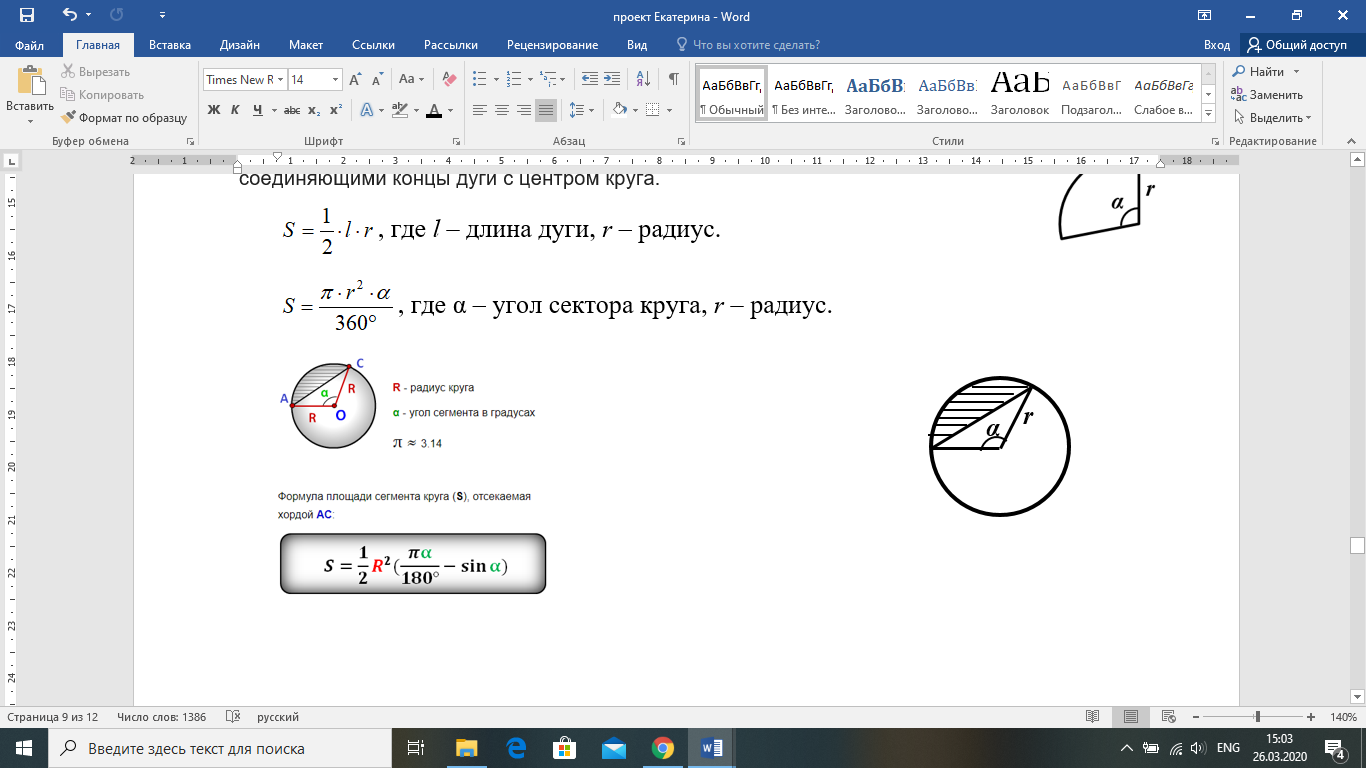, где α – угол сектора круга, r – радиус.

Круговой сегмент — часть круга ограниченная дугой и секущей (хордой).

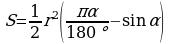
, где α – угол сегмента, r – радиус.

Кольцо — плоская геометрическая фигура, ограниченная двумя окружностями с одним центром.

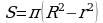, где R – радиус большей окружности, r – радиус меньшей окружности.

Заключение

Умение решать геометрические задачи свидетельствует об одной из самых важных способностей человека – способности понимать текст. Критерием понимания задачи является факт решения задачи. Решая геометрические задачи, мы приучаем себя ориентироваться в ситуациях, становимся более компетентными.

Задачи на нахождение площади представляют в настоящее время интерес для всех людей. В жизни каждый из нас постоянно встречается с необходимостью найти площадь того или иного объекта. Немаловажным является тот факт, что такие задачи выразительно демонстрируют практическую ценность математики.

В ходе выполнения проекта были решены следующие задачи:

Задачи:

1. Изучена литература.

2. Рассмотрены плоские фигуры.

3. Изучены формулы нахождение площадей.

4. Сделана памятка по данной теме.

В ходе работы с проектом я сделала для себя главный вывод: площадь фигуры можно вычислить различными способами и результаты вычислений будут одинаковыми. Но всегда необходимо помнить стандартные формулы нахождения площади плоских фигур, так как они наиболее часто используются не только при решении геометрических задач, но и в нашей жизни.

1. А.В. Погорелов, Геометрия, 7-9 класс. – М.: Просвещение, 2006.

2. Сайт: http://www.fipi.ru

3. Сайт: www.alexlarin.net

Приложение

Основные формулы площадей плоских фигур.