Программа прикладного курса по математике по теме "Задачи с параметрами"

Пояснительная записка

Введение новой формы итоговой аттестации за курс средней школы – Единого Национального Тестирования и широкое использование приёмными комиссиями ВУЗов задач с параметрами в своих экзаменационных материалах ставит перед школой новую задачу – готовить учащихся к решению упражнений данного вида.

Изучение этой темы, ставя перед учениками новые проблемы, стимулирует развитие их математической культуры и навыков аналитического мышления, хорошей техники исследования.

Вместе с тем, в школьном курсе математики эта тема практически не представлена. Восполнить этот пробел возможно за счёт изучения данного прикладного курса.

Особенность этого курса состоит в том, что в процессе занятий учащиеся повторяют ранее изученное, повышают уровень логической подготовки, по-новому видят, анализируют линейные и квадратные многочлены. Программа рассчитана на учащихся 10-11 классов. По мере изучения программного материала усложняются и рассматриваемые в данном курсе вопросы: тригонометрические уравнения и неравенства, содержащие параметр; показательная и логарифмическая функции, соответствующие им параметрические задачи.

Данная программа построена в соответствии с требованиями Государственного образовательного стандарта по математике.

Учебно – тематический план

Тригонометрические уравнения – обзор формул для корней простейших уравнений, классификация тригонометрических уравнений и методов их решения.

Решение тригонометрических уравнений с параметрами (с/р).

Полную информацию смотрите в файле. 

ГУ «Карасорская средняя общеобразовательная школа» Г. Экибастуза Павлодарской области Естественно – математическое направление Математический профиль ЗАДАЧИ С ПАРАМЕТРАМИ прикладной курс по алгебре и началам анализа в 10, 11 классе. Автор программы: учитель математики Гужаковская Татьяна Валентиновна 2013 Пояснительная записка

Введение новой формы итоговой аттестации за курс средней школы – Единого Национального Тестирования и широкое использование приёмными комиссиями ВУЗов задач с параметрами в своих экзаменационных материалах ставит перед школой новую задачу – готовить учащихся к решению упражнений данного вида.

Изучение этой темы, ставя перед учениками новые проблемы, стимулирует развитие их математической культуры и навыков аналитического мышления, хорошей техники исследования.

Вместе с тем, в школьном курсе математики эта тема практически не представлена. Восполнить этот пробел возможно за счёт изучения данного прикладного курса.

Особенность этого курса состоит в том, что в процессе занятий учащиеся повторяют ранее изученное, повышают уровень логической подготовки, по-новому видят, анализируют линейные и квадратные многочлены. Программа рассчитана на учащихся 10-11 классов. По мере изучения программного материала усложняются и рассматриваемые в данном курсе вопросы: тригонометрические уравнения и неравенства, содержащие параметр; показательная и логарифмическая функции, соответствующие им параметрические задачи.

Данная программа построена в соответствии с требованиями Государственного образовательного стандарта по математике.

В результате изучения данного курса обучающиеся должны:

иметь представление:

• линейных уравнениях и неравенствах с параметрами;

• квадратных уравнениях и неравенствах с параметрами;

• показательных, логарифмических, рациональных уравнениях и неравенствах с параметрами;

• тригонометрических уравнениях и неравенствах с параметрами;

• выражениях с модулями и параметрами.

знать:

• аналитические методы решения уравнений и неравенств с параметрами;

• графические методы решения;

• необходимые и достаточные условия в задачах с параметрами.

уметь:

• решать линейные, квадратные, рациональные, иррациональные, тригонометрические, логарифмические и показательные уравнения и неравенства с параметрами;

• пользоваться аналитическими и графическими методами решения заданий с параметрами.

владеть:

• алгоритмами решения уравнений и неравенств с параметрами;

• полным параметрическим анализом многочленов;

• полным параметрическим анализом соотношений с модулем;

• методами условного параметрического анализа.

Курс рассчитан на 68 часов лекционно-практических занятий в 10-11-х классах.

Учебно – тематический план

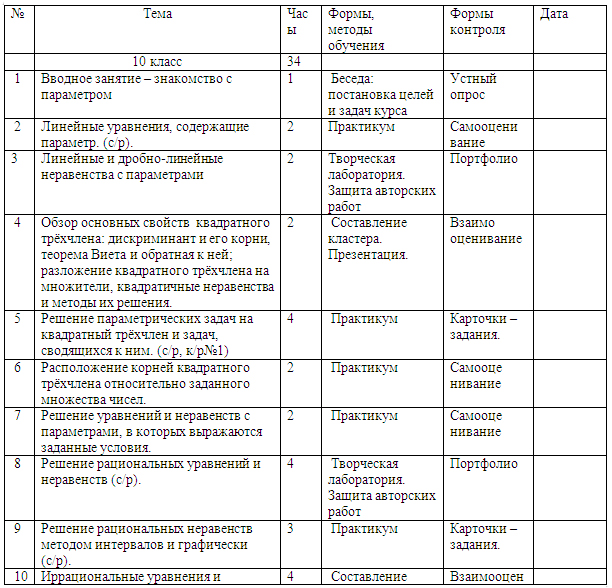
№	Тема	Часы	Формы, методы обучения	Формы контроля	Дата
	10 класс	34
1	Вводное занятие – знакомство с параметром	1	Беседа: постановка целей и задач курса	Устный опрос
2	Линейные уравнения, содержащие параметр. (c/р).	2	Практикум	Самооцени вание
3	Линейные и дробно-линейные неравенства с параметрами	2	Творческая лаборатория. Защита авторских работ	Портфолио
4	Обзор основных свойств квадратного трёхчлена: дискриминант и его корни, теорема Виета и обратная к ней; разложение квадратного трёхчлена на множители, квадратичные неравенства и методы их решения.	2	Составление кластера. Презентация.	Взаимо оценивание
5	Решение параметрических задач на квадратный трёхчлен и задач, сводящихся к ним. (с/р, к/р№1)	4	Практикум	Карточки – задания.
6	Расположение корней квадратного трёхчлена относительно заданного множества чисел.	2	Практикум	Самооце нивание
7	Решение уравнений и неравенств с параметрами, в которых выражаются заданные условия.	2	Практикум	Самооце нивание
8	Решение рациональных уравнений и неравенств (с/р).	4	Творческая лаборатория. Защита авторских работ	Портфолио
9	Решение рациональных неравенств методом интервалов и графически (с/р).	3	Практикум	Карточки – задания.
10	Иррациональные уравнения и неравенства с параметрами (с/р, к/р№2).	4	Составление кластера. Презентация.	Взаимооценивание
11	Тригонометрические уравнения – обзор формул для корней простейших уравнений, классификация тригонометрических уравнений и методов их решения.	2	Практикум	Карточка - задание
12	Решение тригонометрических уравнений с параметрами (с/р).	6	Творческая лаборатория. Защита авторских работ	Портфолио

 Учебно – тематический план

№	Тема	Часы	Формы, методы обучения	Формы контроля	Дата
	11 класс	34
13	Уравнения и неравенства с параметром, содержащие знак модуля (с/р, к/р №3).	4	Творческая лаборатория. Защита авторских работ	Взаимооцени вание.
14	Нахождение числа решений уравнения с параметром графическим способом (с/р).	3	Практикум	Карточки –задания.
15	Системы линейных уравнений с параметрами, способы их решения.	2	Лекция с элементами беседы. Составление алгоритма	Устный ответ
16	Параметрические задачи на касательную к кривой (с/р).	3	Практикум	Карточки – задания.
17	Вычисление наибольшего и наименьшего значений функции в задачах с параметрами (с/р).	4	Творческая лаборатория. Защита авторских работ	Портфо лио
18	Использование монотонности и экстремальных свойств функций тригонометрических, логарифмических и показательных в задачах с параметрами.	3	Составление кластера. Презентация	Взаимооценива ние
19	Необходимые и достаточные условия в задачах с параметрами.	2	Практикум	Самооценивание
20	Логарифмические и показательные уравнения и неравенства, содержащие параметры (с/р,к/р №4).	6	Составление кластера. Презентация	Взаимооцени Вание
21	Задачи с параметрами на Едином Национальном тестировании (с/р).	4	Практикум	Тестиро вание
22	Решение задач по всему курсу.	3	Практикум
24	Итоговое занятие.	1	Зачет

Список литературы для учеников

1. Пособие для подготовки к Единому Национальному тестированию по математике. Алматы, 2005г. И.П. Рустюмова, Т.А. Кузнецова, С.Т. Рустюмова

2. Математика – 1. Учебно – методическое пособие и сборник тестов для поступающих в ВАУЗы. Алматы, 2007г.Исмаил Акйол

3. Математика – 2. Учебно – методическое пособие и сборник тестов для поступающих в ВАУЗы. Алматы, 2007г.Исмаил Акйол

4. Математика для поступающих в ВУЗы. 1 часть. Кокшетау. Н.В. Егоркина

5. Математика для поступающих в ВУЗы. 1 часть. Кокшетау. Н.В. Егоркина

6. Задачи с параметрами. Москва, 2005 г. В.В.Локоть.

7. Джиоев Н.Д. Нахождение графическим способом числа решений уравнения с параметром. - Математика в школе. – 1996-№2-с.54-57.

8. Дорофеев Г.В. О задачах с параметрами, предлагаемых на вступительных экзаменах в ВУЗы. – Математика в школе.-1983 г.-№4- с.36-40.

9. Кочарова К.С.Об уравнениях с параметром и модуле.- Математика в школе.-1995-№2-с.2-4.

Список литературы для учителей

1. Пособие для подготовки к Единому Национальному тестированию по математике. Алматы, 2005г. И.П. Рустюмова, Т.А. Кузнецова, С.Т. Рустюмова

2. Математика – 1. Учебно – методическое пособие и сборник тестов для поступающих в ВАУЗы. Алматы, 2007г.Исмаил Акйол

3. Математика – 2. Учебно – методическое пособие и сборник тестов для поступающих в ВАУЗы. Алматы, 2007г.Исмаил Акйол

4. Математика для поступающих в ВУЗы. 1 часть. Кокшетау. Н.В. Егоркина

5. Математика для поступающих в ВУЗы. 1 часть. Кокшетау. Н.В. Егоркина

6. Иррациональные уравнения и неравенства. С.-Петербург. М, 2008г. А.Х. Шахмейстер

7. Комбинаторика. Статистика, Вероятность. С.-Петербург. М, 2012г. А.Х. Шахмейстер

8. Задачи с параметрами. Москва, 2005 г. В.В.Локоть.

9. Сборник элективных курсов. Математика 8-9 классы. Издательство «Учитель», Волгоград, 2006 г, В.Н. Студенецкая, Л.С. Сагателова

10. Джиоев Н.Д. Нахождение графическим способом числа решений уравнения с параметром. - Математика в школе. – 1996-№2-с.54-57.

11. Дорофеев Г.В. О задачах с параметрами, предлагаемых на вступительных экзаменах в ВУЗы. – Математика в школе.-1983 г.-№4- с.36-40.

12. Кочарова К.С.Об уравнениях с параметром и модуле.- Математика в школе.-1995-№2-с.2-4.

13. Сборник задач по математике для подготовки к вступительным экзаменам, УГНТУ, Уфа 2006 г

ГУ «Карасорская средняя общеобразовательная школа» г. Экибастуза Павлодарской области Естественно – математическое направление Математический профиль ПРАКТИКУМ ПО МАТЕМАТИКЕ прикладной курс по алгебре и началам анализа в 10, 11 классе. Автор программы: учитель математики: Гужаковская Татьяна Валентиновна 2013

Пояснительная записка

Программа рассчитана на 34 часа. Она предназначена для повышения эффективности подготовки учащихся 10 класса к итоговой аттестации математике за курс полной средней школы и предусматривает их подготовку к дальнейшему математическому образованию. Разработана на основе программы по математике для 10 – 11 классов.

Данная программа по математике в 10 классе по теме "Практикум по математике» представляет углубленное изучение теоретического материала укрупненными блоками. Курс рассчитан на учеников общеобразовательного класса, желающих основательно подготовиться к сдаче ЕНТ. В результате изучения этого курса будут использованы приемы парной, групповой деятельности для осуществления элементов самооценки, взаимооценки, умение работать с математической литературой и выделять главное.

Цель курса: на основе коррекции базовых математических знаний учащихся совершенствовать математическую культуру и творческие способности учащихся.

Изучение этого курса позволяет решить следующие задачи:

• формирование у учащихся целостного представления о теме, ее значения в разделе математики, связи с другими темами;

• формирование поисково-исследовательского метода;

• формирование аналитического мышления, развитие памяти, кругозора, умение преодолевать трудности при решении более сложных задач;

• осуществление работы с дополнительной литературой;

• акцентировать внимание учащихся на единых требованиях к правилам оформления различных видов заданий, включаемых в итоговую аттестацию за курс полной общеобразовательной средней школы;

• расширить математические представления учащихся по определённым темам, включённым в программы вступительных экзаменов в другие типы учебных заведений.

Курсу отводится 1 час в неделю. Всего 34 часа.

Умения и навыки учащихся, формируемые курсом:

• навык самостоятельной работы с таблицами и справочной литературой;

• составление алгоритмов решения типичных задач;

• умения решать тригонометрические, показательные и логарифмические уравнения и неравенства;

Особенности курса:

• краткость изучения материала;

• практическая значимость для учащихся;

• нетрадиционные формы изучения материала.

Структура курса

Курс рассчитан на 34 занятия. Включенный в программу материал предполагает изучение и углубление следующих разделов математики:

• Уравнения и неравенства.

• Формулы тригонометрии.

• Тригонометрические функции и их графики.

• Тригонометрические уравнения и неравенства.

• Степень с рациональным показателем.

• Степенная функция.

• Показательная функция.

• Логарифмическая функция.

• Текстовые задачи.

Формы организации учебных занятий

Формы проведения занятий включают в себя лекции, практические работы. Основной тип занятий  комбинированный урок. Каждая тема курса начинается с постановки задачи. Теоретический материал излагается в форме мини - лекции. После изучения теоретического материала выполняются задания для активного обучения, практические задания для закрепления, выполняются практические работы в рабочей тетради, проводится работа с тестами.
Занятия строятся с учётом индивидуальных особенностей обучающихся, их темпа восприятия и уровня усвоения материала.
Систематическое повторение способствует более целостному осмыслению изученного материала, поскольку целенаправленное обращение к изученным ранее темам позволяет учащимся встраивать новые понятия в систему уже освоенных знаний.

Контроль и система оценивания Текущий контроль уровня усвоения материала осуществляется на каждом занятии по результатам выполнения учащимися самостоятельных, практических и тестовых работ. В конце каждой темы учащиеся сдают зачет.

Содержание курса

№ п/п	Тема	Количество часов
1	Уравнения и неравенства.	3
2	Текстовые задачи.	4
3	Формулы тригонометрии.	3
4	Тригонометрические функции и их графики.	2
5	Тригонометрические уравнения и неравенства.	4
6	Степенная функция.	5
7	Показательная функция.	4
8	Логарифмическая функция.	5
9	Задачи с геометрическим содержанием.	4

Содержание программы

Способы решения различных уравнений (линейных, квадратных и сводимых к ним, дробно-рациональных). Способы решения различных неравенств (числовых, линейных, квадратных). Метод интервалов. Область определения выражения.

Тема 2. Текстовые задачи.

Задачи на проценты. Задачи на «движение», на «концентрацию», на «смеси и сплавы», на «работу».

Тема 3. Формулы тригонометрии.

Формулы приведения, сложения, двойных углов и их применение. Применение основных тригонометрических формул к преобразованию выражений.

Тема 4. Тригонометрические функции и их графики.

Обобщить понятие тригонометрических функций; свойства функций и умение строить графики.

Тема 5. Тригонометрические уравнения.

Сформировать умения решать простейшие тригонометрические уравнения; ознакомить с некоторыми приемами решения тригонометрических уравнений.

Тема 6. Степенная функция.

Обобщить понятие степенной функцией с действительным показателем, ее свойства и умение строить ее график; знакомство с разными способами решения иррациональных уравнений; обобщение понятия степени числа и корня n-й степени.

Тема 7. Показательная функция.

Систематизировать понятие показательной функции; ее свойств и умение строить ее график; познакомиться со способами решения показательных уравнений и неравенств.

Тема 8. Логарифмическая функция.

Обобщить понятие логарифмической функции; ее свойства и умение строить ее график; знакомство с разными способами решения логарифмических уравнений и неравенств.

Тема 9. Задачи с геометрическим содержанием.

Действия с геометрическими фигурами, координатами и векторами. Планиметрические задачи на нахождение геометрических величин (длин, углов, площадей).

Учебно – тематический план

№ п/п	Тема	Часы	Формы, методы обучения	Формы контроля	Дата
	Введение
	1. Уравнения и неравенства	3
1	Способы решения линейных, квадратных и дробно-рациональных уравнений.		Лекция с элементами беседы	Устная форма
2	Способы решения линейных, квадратных неравенств. Метод интервалов.		Практикум	Самооцени вание
3	Способы решения систем уравнений и неравенств.		Практикум	Взаимооцени вание
	2. Текстовые задачи	4
4	Решение задач на проценты, на «концентрацию», на «смеси и сплавы».		Практикум	Взаимооцени вание
5	Задачи на «движение», на «работу».		Практикум	Самооценива ние
6	Решение комбинаторных задач.		Составление кластера. Презентация
7	Зачет №1 по теме «Решение текстовых задач и уравнений».
	3. Формулы тригонометрии	3
8	Основные тригонометрические формулы и их применение.		Исследовательская работа
9	Преобразование выражений с помощью формул тригонометрии.		Практикум	Карточки - задания
10	Применение основных тригонометрических формул к преобразованию выражений.		Практикум	Карточки задания
	4. Тригонометрические функции и их графики	2
11	Построение графиков тригонометричес-ких функций.		Лекция с элементами беседы	Устные ответы
12	Исследование тригонометрических функций.		Практикум	Карточки - задания
	5. Тригонометрические уравнения	4
13	Решение простейших тригонометричес-ких уравнений.		Практикум	Самооценивание
14	Решение однородных тригонометрических уравнений.		Практикум	Взаимооценивание
15	Способы решения тригонометрических уравнений		Творческая лаборатория. Защита авторских работ
16	Зачет №2 по теме «Исследование тригонометрических функции и решение тригонометрических уравнений».
	6. Степенная функция	5
17	Степенная функция, ее свойства и график.		Составление кластера Презентация	Взаимооценивание
18	Преобразование степенных и иррациональных выражений.		Практикум	Карточки - задания
19	Решение иррациональных уравнений.		Практикум	Взаимооце нивание
20	Способы решения иррациональных уравнений.		Практикум	Карточки - задания
21	Зачет №3 по теме «Степенная функция».
	7. Показательная функция	4
22	Показательная функция, ее свойства и график.		Составление кластера Презентация	Взаимооце нивание
23	Способы решения показательных уравнений.		Практикум	Карточки - задания
24	Решение показательных неравенств.		Практикум	Взаимооце нивание
25	Зачет №4 по теме «Показательная функция».
	8. Логарифмическая функция	5
26	Применение свойств логарифмов в преобразованиях выражений.		Творческая лаборатория. Защита проектов
27	Логарифмическая функция, ее свойства и график.		Практикум	Карточки - задания
28	Способы решения логарифмических уравнений.		Практикум	Карточки - задания
29	Решение логарифмических неравенств.		Практикум	Самооцени вание
30	Зачет №5 по теме «Логарифмическая функция».
	9. Задачи с геометрическим содержанием	4
31	Действия с геометрическими фигурами, координатами и векторами.		Лекция с элементами беседы	Устный опрос
32	Планиметрические задачи на нахождение геометрических величин (длин, углов, площадей).		Практикум	Взаимооце нивание
33	Зачет №6 по теме «Геометрические задачи».
34	Простейшие стереометрические задачи на нахождение площадей поверхностей многогранников.		Практикум	Карточки - задания
	ИТОГО:	34

Список литературы для учеников

1. Пособие для подготовки к Единому Национальному тестированию по математике. Алматы, 2005г. И.П. Рустюмова, Т.А. Кузнецова, С.Т. Рустюмова

2. Математика – 1. Учебно – методическое пособие и сборник тестов для поступающих в ВАУЗы. Алматы, 2007г.Исмаил Акйол

3. Математика – 2. Учебно – методическое пособие и сборник тестов для поступающих в ВАУЗы. Алматы, 2007г.Исмаил Акйол

4. Математика для поступающих в ВУЗы. 1 часть. Кокшетау. Н.В. Егоркина

5. Математика для поступающих в ВУЗы. 1 часть. Кокшетау. Н.В. Егоркина

6. Задачи с параметрами. Москва, 2005 г. В.В.Локоть.

7. Джиоев Н.Д. Нахождение графическим способом числа решений уравнения с параметром. - Математика в школе. – 1996-№2-с.54-57.

8. Дорофеев Г.В. О задачах с параметрами, предлагаемых на вступительных экзаменах в ВУЗы. – Математика в школе.-1983 г.-№4- с.36-40.

9. Кочарова К.С.Об уравнениях с параметром и модуле.- Математика в школе.-1995-№2-с.2-4.

Список литературы для учителей

1. Пособие для подготовки к Единому Национальному тестированию по математике. Алматы, 2005г. И.П. Рустюмова, Т.А. Кузнецова, С.Т. Рустюмова

2. Математика – 1. Учебно – методическое пособие и сборник тестов для поступающих в ВАУЗы. Алматы, 2007г.Исмаил Акйол

3. Математика – 2. Учебно – методическое пособие и сборник тестов для поступающих в ВАУЗы. Алматы, 2007г.Исмаил Акйол

4. Математика для поступающих в ВУЗы. 1 часть. Кокшетау. Н.В. Егоркина

5. Математика для поступающих в ВУЗы. 1 часть. Кокшетау. Н.В. Егоркина

6. Иррациональные уравнения и неравенства. С.-Петербург. М, 2008г. А.Х. Шахмейстер

7. Комбинаторика. Статистика, Вероятность. С.-Петербург. М, 2012г. А.Х. Шахмейстер

8. Задачи с параметрами. Москва, 2005 г. В.В.Локоть.

9. Сборник элективных курсов. Математика 8-9 классы. Издательство «Учитель», Волгоград, 2006 г, В.Н. Студенецкая, Л.С. Сагателова

10. Джиоев Н.Д. Нахождение графическим способом числа решений уравнения с параметром. - Математика в школе. – 1996-№2-с.54-57.

11. Дорофеев Г.В. О задачах с параметрами, предлагаемых на вступительных экзаменах в ВУЗы. – Математика в школе.-1983 г.-№4- с.36-40.

12. Кочарова К.С.Об уравнениях с параметром и модуле.- Математика в школе.-1995-№2-с.2-4.

13. Сборник задач по математике для подготовки к вступительным экзаменам, УГНТУ, Уфа 2006 г

Пояснительная записка

Настоящая программа написана на основе программы для общеобразовательных школ, гимназий, лицеев.

Программа предназначена для работы с учащимися 11 класса с целью повышения эффективности обучения их математике, предусматривает подготовку их к государственной (итоговой) аттестации по математике за курс полной средней школ. Программа рассчитана на 34 учебных часа. Содержание программы соответствует по тематическому содержанию программе по математике для 5-11 классов общеобразовательных школ.

Прикладной курс «Практикум по математике» в 11 классе представляет собой повторение, обобщение и углубленное изучение теоретического материала укрупненными блоками по наиболее значимым темам: «Выражения», «Уравнения и неравенства», «Функции и графики», «Элементы статистики, комбинаторики и теории вероятностей», «Решение задач по геометрии». Курс рассчитан на учащихся общеобразовательного класса, желающих хорошо подготовиться к ЕНТ и к дальнейшему изучению математики в ВУЗах.

В процессе изучения курса будут использованы приемы индивидуальной, парной, групповой деятельности для осуществления самооценки, взаимоконтроля; развиваться умения и навыки работы с математической литературой и использования интернет-ресурсов.

Цель курса:

• Коррекция и углубление конкретных математических знаний, необходимых для прохождения государственной (итоговой) аттестации за курс средней полной школы в форме экзамена и по материалам ЕНТ, для изучения смежных дисциплин, для продолжения образования.

• Интеллектуальное развитие учащихся, формирование качеств мышления, характерных для математической деятельности и необходимых для продуктивной жизни в обществе.

Задачи:

• Систематическое повторение учебного материала по основным темам курса алгебры и начал анализа и геометрии.

• Оказание практической коррекционной помощи учащимся в изучении отдельных тем предмета.

• Формирование поисково-исследовательского метода.

• Акцентирование внимания учащихся на единых требованиях к правилам оформления решения различных заданий.

• Осуществление тематического контроля на основе мониторинга выполнения учащимися типовых заданий.

• Получение школьниками дополнительных знаний по математике.

• Воспитание культуры личности, отношения к математике как части общечеловеческой культуры, играющей особую роль в общественном развитии.

СОДЕРЖАНИЕ ОБУЧЕНИЯ:

1 Выражения

Числа, корни и степени

1. Степень с натуральным, целым, рациональным показателем

2. Дроби, проценты, рациональные числа

3. Корень степени n 1 и его свойства

Основы тригонометрии

4. Синус, косинус, тангенс и котангенс числа

5. Основные тригонометрические тождества

6. Формулы приведения

Логарифмы

7. Логарифм числа и его свойства.

Преобразования выражений

8. Преобразования алгебраических выражений.

9. Преобразования тригонометрических выражений

10. Преобразование логарифмических выражений.

2 Уравнения и неравенства

Уравнения

11. Квадратные уравнения

12. Рациональные уравнения

13. Иррациональные уравнения

14. Тригонометрические уравнения

15. Показательные уравнения

16. Логарифмические уравнения

17. Системы уравнений с двумя неизвестными

Неравенства

18. Квадратные неравенства

19. Рациональные неравенства

20. Показательные неравенства

21. Логарифмические неравенства

22. Метод интервалов

23. Системы неравенств

3 Функции и графики

24. Основные свойства функций.

25. Функциональная зависимость в реальных процессах.

26. Графический подход к решению задач с параметрами.

4 Элементы статистики, комбинаторики и теории вероятностей

27. Статистические характеристики.

28.Формулы комбинаторики.

29.Вероятностно-комбинаторные задачи.

5 Решение задач по геометрии.

30. Решение треугольников.

31. Практические задачи по геометрии.

32. Многогранники и тела вращения.

6 Итоговое занятие. Контроль и оценка результатов изучения курса.

33. Обобщающий урок по курсу практикума.

34. Тренировочно-диагностическая работа.

ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ:

№ п/п	Разделы, темы	К-во часов
	1 Выражения.	10
1	Числа, корни и степени.	3
2	Основы тригонометрии.	3
3	Логарифмы.	1
4	Преобразования выражений.	3
	2 Уравнения и неравенства.	13
5	Уравнения.	7
6	Неравенства.	6
	3 Функции и графики.	3
	4 Элементы статистики, комбинаторики и теории вероятностей.	3
	5 Решение задач по геометрии.	3
	6 Итоговое занятие. Контроль и оценка результатов изучения курса.	2
	Итого	34

Требования к уровню математической подготовки

выпускников 11 класса

В результате изучения курса учащиеся 11 класса должны уметь:

• находить значения корня натуральной степени, степени с рациональным показателем, логарифма, значения тригонометрических выражений на основе определений и основных свойств, пользоваться оценкой и прикидкой при практических расчетах;

• выполнять тождественные преобразования тригонометрических, иррациональных, степенных, показательных и логарифмических выражений;

• вычислять значения числовых и буквенных выражений, осуществляя необходимые подстановки и преобразования;

• определять значения функции по значению аргумента при различных способах задания функции;

• описывать по графику и в простейших случаях по формуле поведение и свойства функций;

• строить графики линейной, квадратичной, тригонометрических, степенной, показательной и логарифмической функций;

• решать уравнения, простейшие системы уравнений, используя свойства функций и их графиков;

• решать рациональные, тригонометрические, иррациональные, показательные и логарифмические уравнения, их системы;

• решать рациональные, показательные и логарифмические неравенства, их системы;

• составлять уравнения и неравенства по условию задачи;

• использовать для приближенного решения уравнений и неравенств графический метод;

• изображать на координатной плоскости множества решений простейших уравнений и их систем;

• вычислять производные и первообразные элементарных функций;

исследовать в простейших случаях функции на монотонность, находить наибольшие и наименьшие значения функций, строить графики многочленов и простейших рациональных функций с использованием аппарата математического анализа;

• решать геометрические задачи с применением соотношений и пропорциональных отрезков в прямоугольном треугольнике, основных теорем для произвольного треугольника;

• решать геометрические задачи на клетчатой бумаге.

Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:

• построения и исследования простейших математических моделей.

Умения и навыки учащихся, формируемые прикладным курсом:

• навыки коллективной и самостоятельной работы со справочной литературой и таблицами;

• эффективное использование дополнительной литературы и интернет-ресурсов для самообучения и самоконтроля;

• составление и использование алгоритмов решения типичных задач практической направленности;

• умения решать уравнения и неравенства, задачи различного вида;

• умения исследовать элементарные функции при решении разных задач.

учащийся должен знать/понимать

• математические формулы, методы решения уравнений и неравенств, приемы применения их для решения задач;

• как можно функционально описать реальные зависимости;

• основные алгоритмы решения примеров и задач;

• решать задания, приближенные к заданиям ЕНТ.

Методические рекомендации по реализации программы:

Основным дидактическим средством для данного курса являются тексты типовых задач, которые могут быть выбраны из сборников, тренировочных вариантов ЕНТ, интернет-банков заданий, текстов краевых диагностических работ или составлены самим учителем.

Учащиеся обеспечиваются раздаточным материалом, подготовленным на основе предлагаемого ниже списка литературы.

Для повышения эффективности работы учащихся используются мультимедийные ресурсы обучающего и контролирующего характера.

Учебно-тематический план

№ п/п	Разделы, темы	Кол-во часов	Формы, методы обучения	Формы контроля
1	Выражения.	10
	Числа, корни и степени	3
1	Степень с натуральным, целым, рациональным показателем.	1	Составление кластера Презинтация	Взаимооценивание
2	Дроби, проценты, рациональные числа.	1	Практикум	Самооценивание
3	Корень степени n 1 и его свойства.	1	Практикум	Карточки – задания.
	Основы тригонометрии	3
4	Синус, косинус, тангенс и котангенс числа.	1	Лекция с элементами беседы	Устный опрос
5	Основные тригонометрические тождества.	1	Практикум	Карточки – задания
6	Формулы приведения.	1	Практикум	Взаимооценивание
	Логарифмы	1
7	Логарифм числа и его свойства.	1	Практикум	Самооценивание
	Преобразования выражений	3
8	Преобразования алгебраических выражений.	1	Творческая мастерская Защита работ	Взаимооценивание
9	Преобразования тригонометрических выражений	1	Практикум	Карточки – задания.
10	Преобразование логарифмических выражений.	1	Практикум	Самооценивание
2	Уравнения и неравенства	13
	Уравнения.	7
11	Квадратные уравнения	1	Составление кластера Презентация	Взаимооценивание
12	Рациональные уравнения	1	Практикум	Карточки – задания.
13	Иррациональные уравнения	1	Практикум	Самооценивание
14	Тригонометрические уравнения	1	Практикум	Взаимооценивание
15	Показательные уравнения	1	Практикум	Карточки - задания
16	Логарифмические уравнения	1	Практикум	Карточки - задания
17	Системы уравнений с двумя неизвестными	1	Творческая лаборатория Защита работ	Взаимооценивание
	Неравенства	6
18	Квадратные неравенства	1	Составления кластера по теме Презентация	Взаимооценивание
19	Рациональные неравенства	1	Практикум	Карточки - задания
20	Показательные неравенства	1	Практикум	Самооценивание
21	Логарифмические неравенства	1	Практикум	Карточки - задания
22	Метод интервалов	1
23	Системы неравенств	1	Практикум	Взаимооценивание
3	Функции и графики	3
	Элементарное исследование функций	3
24	Основные свойства функций.	1	Составление кластера. Презинтация	Взаимооценивание
25	Функциональная зависимость в реальных процессах.	1	Практикум	Карточки - задания
26	Графический подход к решению задач с параметрами.	1	Практикум	Карточки - задания
4	Элементы статистики, комбинаторики и теории вероятностей	3
27	Статистические характеристики.	1	Лекция с элементами беседы	Устный опрос
28	Формулы комбинаторики.	1	Практикум	Карточки - задания
29	Вероятностно-комбинаторные задачи.	1	Практикум	Карточки - задания
5	Решение задач по геометрии.	3
30	Решение треугольников.	1	Мастер класс
31	Практические задачи по геометрии	1	Практикум	Взаимооценивание
32	Многогранники и тела вращения.	1	Практикум	Самооценивание
6	Итоговое занятие. Контроль и оценка результатов изучения курса	2
33	Тренировочно-диагностическая работа.	1	Практикум	Карточки -задания
34	Обобщающий урок по курсу практикума.	1

Список литературы для учеников

1.Пособие для подготовки к Единому Национальному тестированию по математике. Алматы, 2005г. И.П. Рустюмова, Т.А. Кузнецова, С.Т. Рустюмова

2.Математика – 1. Учебно – методическое пособие и сборник тестов для поступающих в ВАУЗы. Алматы, 2007г.Исмаил Акйол

3.Математика – 2. Учебно – методическое пособие и сборник тестов для поступающих в ВАУЗы. Алматы, 2007г.Исмаил Акйол

4.Математика для поступающих в ВУЗы. 1 часть. Кокшетау. Н.В. Егоркина

5.Математика для поступающих в ВУЗы. 1 часть. Кокшетау. Н.В. Егоркина

6.Задачи с параметрами. Москва, 2005 г. В.В.Локоть.

7.Джиоев Н.Д. Нахождение графическим способом числа решений уравнения с параметром. - Математика в школе. – 1996-№2-с.54-57.

8.Дорофеев Г.В. О задачах с параметрами, предлагаемых на вступительных экзаменах в ВУЗы. – Математика в школе.-1983 г.-№4- с.36-40.

9.Кочарова К.С.Об уравнениях с параметром и модуле.- Математика в школе.-1995-№2-с.2-4

Список литературы для учителей

1. Пособие для подготовки к Единому Национальному тестированию по математике. Алматы, 2005г. И.П. Рустюмова, Т.А. Кузнецова, С.Т. Рустюмова

2. Математика – 1. Учебно – методическое пособие и сборник тестов для поступающих в ВАУЗы. Алматы, 2007г.Исмаил Акйол

3. Математика – 2. Учебно – методическое пособие и сборник тестов для поступающих в ВАУЗы. Алматы, 2007г.Исмаил Акйол

4. Математика для поступающих в ВУЗы. 1 часть. Кокшетау. Н.В. Егоркина

5. Математика для поступающих в ВУЗы. 1 часть. Кокшетау. Н.В. Егоркина

6. Иррациональные уравнения и неравенства. С.-Петербург. М, 2008г. А.Х. Шахмейстер

7. Комбинаторика. Статистика, Вероятность. С.-Петербург. М, 2012г. А.Х. Шахмейстер

8. Задачи с параметрами. Москва, 2005 г. В.В.Локоть.

9. Сборник элективных курсов. Математика 8-9 классы. Издательство «Учитель», Волгоград, 2006 г, В.Н. Студенецкая, Л.С. Сагателова

10. Джиоев Н.Д. Нахождение графическим способом числа решений уравнения с параметром. - Математика в школе. – 1996-№2-с.54-57.

11. Дорофеев Г.В. О задачах с параметрами, предлагаемых на вступительных экзаменах в ВУЗы. – Математика в школе.-1983 г.-№4- с.36-40.

12. Кочарова К.С.Об уравнениях с параметром и модуле.- Математика в школе.-1995-№2-с.2-4.

13. Сборник задач по математике для подготовки к вступительным экзаменам, УГНТУ, Уфа 2006 г