«_____»____________ 2013 г.
Программа учебной дисциплины «Математика » обсуждена и одобрена на заседании Цикловой методической комиссии
Рабочая программа учебной дисциплины «Математика» является частью общеобразовательной подготовки обучающих в учреждениях НПО. Составлена на основе примерной программы среднего (полного) общего образования по математике (профильный уровень) для профессий НПО.
Учебная дисциплина «Математика» относится к циклу общеобразовательной подготовки.
Основу программы составляет содержание, согласованное с требованиями федерального компонента государственного стандарта среднего (полного) общего образования базового уровня.
широту и в то же время ограниченность применения математических методов к анализу
- находить значения корня, степени, логарифма, тригонометрических выражений на
- выполнять преобразования выражений, применяя формулы, связанные со свойствами
степеней, логарифмов, тригонометрических функций.
- вычислять значение функции по значению аргумента при различных способах задания
- определять основные свойства числовых функций, иллюстрировать их на графиках;
- строить графики изученных функций, иллюстрировать по графику свойства элементарных
- находить производные элементарных функций; использовать производную для изучения
- решать рациональные, показательные, логарифмические, тригонометрические уравнения,
- использовать графический метод решения уравнений и неравенств; изображать на
координатной плоскости решения уравнений, неравенств и систем с двумя неизвестными;
- составлять и решать уравнения и неравенства, связывающие неизвестные величины в
текстовых (в том числе прикладных) задачах.
- решать простейшие комбинаторные задачи методом перебора, а также с использованием
известных формул; вычислять в простейших случаях вероятности событий на основе
- распознавать на чертежах и моделях пространственные формы; соотносить трехмерные
- описывать взаимное расположение прямых и плоскостей в пространстве, аргументировать
свои суждения об этом расположении; анализировать в простейших случаях взаимное
- изображать основные многогранники и круглые тела; выполнять чертежи по условиям
задач; строить простейшие сечения куба, призмы, пирамиды; решать планиметрические и
простейшие стереометрические задачи на нахождение геометрических величин (длин,
- использовать приобретенные знания и умения в практической деятельности и повседневной
жизни.
самостоятельной работы обучающегося148 часов.
|
Наименование разделов и тем | Содержание учебного материала, лабораторные работы и практические занятия, самостоятельная работа обучающихся | Объем часов | Уровень освоения |
| Обяз. | ТО | Пр | Ср |
| 1 | 2 | 3 | 4 |
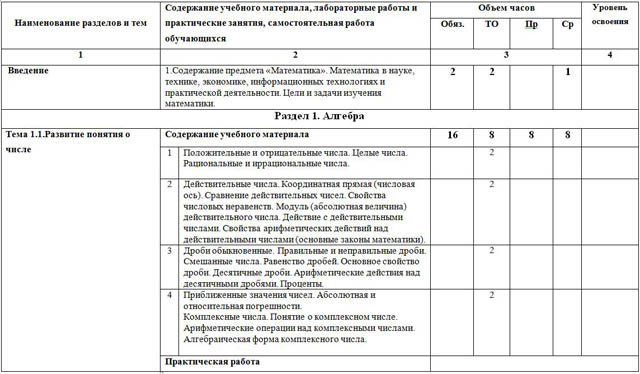
| Введение | 1.Содержание предмета «Математика». Математика в науке, технике, экономике, информационных технологиях и практической деятельности. Цели и задачи изучения математики. | 2 | 2 |
| 1 |
|
| Раздел 1. Алгебра |
| Тема 1.1.Развитие понятия о числе
| Содержание учебного материала | 16 | 8 | 8 | 8 |
|
| 1 | Положительные и отрицательные числа. Целые числа. Рациональные и иррациональные числа. |
| 2 |
|
|
|
| 2 | Действительные числа. Координатная прямая (числовая ось). Сравнение действительных чисел. Свойства числовых неравенств. Модуль (абсолютная величина) действительного числа. Действие с действительными числами. Свойства арифметических действий над действительными числами (основные законы математики). |
| 2 |
|
|
|
| 3 | Дроби обыкновенные. Правильные и неправильные дроби. Смешанные числа. Равенство дробей. Основное свойство дроби. Десятичные дроби. Арифметические действия над десятичными дробями. Проценты. |
| 2 |
|
|
|
| 4 | Приближенные значения чисел. Абсолютная и относительная погрешности. Комплексные числа. Понятие о комплексном числе. Арифметические операции над комплексными числами. Алгебраическая форма комплексного числа.
|
| 2 |
|
|
|
| Практическая работа |
|
| 1 | Выполнить арифметические действия над обыкновенными дробями. |
|
| 2 |
|
|
| 2 | Выполнить арифметические действия над десятичными дробями. |
|
| 2 |
|
|
| 3 | Приближенные вычисления чисел. |
|
| 2 |
|
|
| 4 | Контрольная работа |
|
| 2 |
|
|
| Самостоятельная работа |
|
| 1 | Найти значение числового выражения. |
|
|
| 2 |
|
| 2 | Реферат «Исторические сведения о дробях». |
|
|
| 2 |
|
| 3 | Изучить тему «Сложные проценты». |
|
|
| 2 |
|
| 4 | Задачи на проценты |
|
|
| 2 |
|
| Тема 1.2. Основы тригонометрии. | Содержание учебного материала. | 40 | 16 | 24 | 20 |
|
| 1 | Введение. |
| 2 |
|
|
|
| 2 | Радианная мера угла. Тригонометрические функции (синус, косинус, тангенс, котангенс). |
| 2 |
|
|
|
| 3 | Обратные тригонометрические функции. |
| 2 |
|
|
|
| 4 | Основные тригонометрические тождества, формулы приведения. |
| 2 |
|
|
|
| 5 | Преобразование простейших тригонометрических выражений. |
| 2 |
|
|
|
| 6 | Простейшие тригонометрические уравнения. |
| 2 |
|
|
|
| 7 | Простейшие тригонометрические неравенства. |
| 2 |
|
|
|
| 8 | Решение систем тригонометрических выражений. |
| 2 |
|
|
|
| Практическая работа |
|
| 1 | Определить радианную меру угла. |
|
| 2 |
|
|
| 2 | Определить градусную меру угла. |
|
| 2 |
|
|
| 3 | Вычислить выражение. |
|
| 2 |
|
|
| 4 | Вычислить синус, косинус, тангенс, котангенс. |
|
| 2 |
|
|
| 5 | Упростить тригонометрическое выражение. |
|
| 2 |
|
|
| 6 | Упростить тригонометрическое выражение |
|
| 2 |
|
|
| 7 | Упростить выражение. |
|
| 2 |
|
|
| 8 | Доказать тождество. |
|
| 2 |
|
|
| 9 | Решить тригонометрическое уравнение. |
|
| 2 |
|
|
| 10 | Решить и упростить тригонометрическое уравнение. |
|
| 2 |
|
|
| 11 | Решить систему тригонометрических уравнений. |
|
| 2 |
|
|
| 12 | Контрольная работа |
|
| 2 |
|
|
| Самостоятельная работа. |
|
| 1 | Упростить тригонометрическое выражение. |
|
|
| 2 |
|
| 2 | Доказать тождество. |
|
|
| 2 |
|
| 3 | Вычислить синус, если известно выражения косинуса. |
|
|
| 2 |
|
| 4 | Вычислить косинус, если известно выражения синуса. |
|
|
| 2 |
|
| 5 | Решение тригонометрических уравнений с применением комбинированных способов. |
|
|
| 2 |
|
| 6 | Решение тригонометрических уравнений, содержащие обратные тригонометрические функции. |
|
|
| 2 |
|
| 7 | Решение системы тригонометрических уравнений. |
|
|
| 2 |
|
| 8 | Решение тригонометрических неравенств. |
|
|
| 2 |
|
| 9 | Определить знак тригонометрических выражений. |
|
|
| 2 |
|
| 10 | Изучить тригонометрические величины: секанс угла и косеканс угла. Задания на сварку под углом. Расчет синуса и косинуса угла. Измерения при сварке фигур треугольной формы |
|
|
| 2 |
|
| Тема 1.3. Функции, и их свойства и график. Степенные, показательные, логарифмические и тригонометрические функции.
| Содержание учебного материала. | 22 | 8 | 14 | 11 |
|
| 1 | Определение и свойства функции. |
| 2 |
|
|
|
| 2 | Виды функции. |
| 2 |
|
|
|
| 3 | Определение синус, косинус, тангенс, котангенс. Знаки тригонометрических функций по четвертям числовой окружности. Свойства тригонометрических функций. |
| 2 |
|
|
|
| 4 | Преобразование графиков. |
| 2 |
|
|
|
| Практическая работа |
|
| 1 | Определить область определения функции аналитически. |
|
| 2 |
|
|
| 2 | Построить график функции. |
|
| 2 |
|
|
| 3 | Исследовать функцию на четность и нечетность. |
|
| 2 |
|
|
| 4 | Исследовать функцию и построить график. |
|
| 2 |
|
|
| 5 | Способы построения графика квадратной функции. |
|
| 2 |
|
|
| 6 | Записать уравнение линейной функции. |
|
| 2 |
|
|
| 7 | Контрольная работа |
|
| 2 |
|
|
| Самостоятельная работа |
|
| 1 | По графикам указать свойства функции. |
|
|
| 2 |
|
| 2 | Укажите периодичность и не периодичность функции. |
|
|
| 2 |
|
| 3 | На каком из рис. изображены графики функции. |
|
|
| 2 |
|
| 4 | Найти область определения функции. |
|
|
| 2 |
|
| 5 | Заполни пропуски. |
|
|
| 2 |
|
| 6 | Найдите длину интервала, являющейся областью определения функции. Задачи с производственным содержанием по теме «Показательная функция»
|
|
|
| 1 |
|
| Тема 1.4. Корни, степени и логарифмы. | Содержание учебного материала | 36 | 14 | 22 | 18 |
|
| 1 | Степень натурального числа с натуральным показателем. Степень действительного числа с натуральным показателем. Свойства степеней. Степень с нулевым и отрицательным целым показателем. |
| 2 |
|
|
|
| 2 | Одночлен и многочлен. Преобразование суммы и разности многочленов. |
| 2 |
|
|
|
| 3 | Целые рациональные выражения. Дробные рациональные выражения. Возведения рациональных дробей в степень. |
| 2 |
|
|
|
| 4 | Корень п-й степени из действительного числа. Основные свойства корней. Внесение множителя под корень. Вынесение множителя из-под корня. |
| 2 |
|
|
|
| 5 | Освобождение дроби от иррациональности в знаменатель дроби или в числитель дроби. Подобные радикалы. Приведения подкоренного выражения к целому виду. |
| 2 |
|
|
|
| 6 | Степень действительного числа с рациональным показателем. |
| 2 |
|
|
|
| 7 | Степень действительного числа с действительным показателем. Свойства степени действительного числа с действительными показателями. |
| 2 |
|
|
|
| Практическая работа |
|
|
|
|
|
| 1 | Вычислить арифметический корень из числа. |
|
| 2 |
|
|
| 2 | Решить показательные уравнения. |
|
| 2 |
|
|
| 3 | Вычислить выражения. |
|
| 2 |
|
|
| 4 | Вычислить выражения. |
|
| 2 |
|
|
| 5 | Упростить выражения. |
|
| 2 |
|
|
| 6 | Вычислить показательное выражение |
|
| 2 |
|
|
| 7 | Упростить выражения. |
|
| 2 |
|
|
| 8 | Вычислить логарифмическое выражение |
|
| 2 |
|
|
| 9 | Вычислить логарифмическое выражение |
|
| 2 |
|
|
| 10 | Выразить логарифм через натуральный. |
|
| 2 |
|
|
| 11 | Контрольная работа. |
|
| 2 |
|
|
| Самостоятельная работа. |
|
|
|
|
|
| 1 | Изучить натуральную степень комплексного числа |
|
|
| 2 |
|
| 2 | Изучить корень п-й степени из комплексного числа. |
|
|
| 2 |
|
| 3 | Узнать о происхождении терминов и обозначений. |
|
|
| 2 |
|
| 4 | Реферат «Из истории логарифмов». |
|
|
| 2 |
|
| 5 | Изучить применение логарифмов в геометрии. |
|
|
| 2 |
|
| 6 | Изучить преобразование выражений, содержащей степени с дробными показателями. |
|
|
| 2 |
|
| 7 | Изучить преобразование выражений, содержащие степени. |
|
|
| 2 |
|
| 8 | Изучить преобразование выражений, содержащие логарифмы. |
|
|
| 2 |
|
| 9 | Реферат «Применение логарифмов в профессии сварщик». |
|
|
| 2 |
|
| Раздел 2. Начала математического анализа. |
| Тема 2.1. Начала математического анализа. |
Содержание учебного материала | 34 | 14 | 20 | 17 |
|
| 1 | Определение последовательности. Возрастание и убывания последовательности. Определение арифметической прогрессии. Свойства арифметической прогрессии. |
| 2 |
|
|
|
| 2 | Определение геометрической прогрессии. Понятие о пределе последовательности. Сумма бесконечной геометрической прогрессии. |
| 2 |
|
|
|
| 3 | Предел функции. |
| 2 |
|
|
|
| 4 | Производная. Приращения аргумента. Приращение функции. Определение производной. Формулы дифференцирования. Таблица производных. Уравнение касательной к графику функции. |
| 2 |
|
|
|
| 5 | Дифференцирования суммы, произведения, частного. Сложная функция и ее дифференцирования. Физический смысл производной. |
| 2 |
|
|
|
| 6 | Вторая производная и ее физический смысл. Касательная к графику функции. Применение производной к исследованию функции на монотонность, экстремумы. Общая схема построения графика функции. |
| 2 |
|
|
|
| 7 | Первообразная и интеграл. |
| 2 |
|
|
|
| Практическая работа |
|
| 1 | Вычисление арифметической прогрессии. |
|
| 2 |
|
|
| 2 | Задачи на вычисление арифметической прогрессии. |
|
| 2 |
|
|
| 3 | Задачи на вычисление геометрической прогрессии. |
|
| 2 |
|
|
| 4 | Определить производные функции. |
|
| 2 |
|
|
| 5 | Определить производную сложной функции. |
|
| 2 |
|
|
| 6 | Составить уравнение касательной к графику функции. |
|
| 2 |
|
|
| 7 | Исследовать функцию и построить график. |
|
| 2 |
|
|
| 8 | Задачи на нахождения наименьшего и наибольшего значения функции. |
|
| 2 |
|
|
| 9 | Определить приращение функции. |
|
| 2 |
|
|
| 10 | Контрольная работа « Элементы дифференциального исчисления» |
|
| 2 |
|
|
| Самостоятельная работа |
|
| 1 | Выполнить тест «Прогрессия» |
|
|
| 1 |
|
| 2 | Нахождение производной сложной функции. |
|
|
| 1 |
|
| 3 | Исследовать функцию и построить график. |
|
|
| 1 |
|
| 4 | Привести примеры применения интеграла в физике и геометрии. |
|
|
| 1 |
|
| 5 | Решение задач с применением второй производной. |
|
|
| 1 |
|
| 6 | Решение задач на движение. |
|
|
| 1 |
|
| 7 | Найти коэффициент наклона касательной к графику функции. |
|
|
| 1 |
|
| 8 | Найти угловой коэффициент касательной к графику функции. |
|
|
| 1 |
|
| 9 | Указать абсциссу точки графика функции, в которой угловой коэффициент равен нулю. |
|
|
| 1 |
|
| 4 | Найти абсциссу точки. |
|
|
| 2 |
|
| 5 | Найти тангенс угла наклона касательной, проведенной к графику функции. |
|
|
| 2 |
|
| 6 | Вычислить производную сложной тригонометрической функции. |
|
|
| 1 |
|
| 7 | Вычислить производную сложной степенной функции. |
|
|
| 1 |
|
| 8 | Вычислить производную произведения функций. |
|
|
| 1 |
|
| 9 | Задачи на построение графиков, на нахождение промежутков возрастания и убывания функций
|
|
|
| 1 |
|
| Тема 2.2. Уравнения и неравенства. |
Содержание учебного материала | 30 | 12 | 18 | 15 |
|
| 1 | Определения уравнения. Корни уравнений. Равносильность уравнений. Квадратные уравнения. Неполные квадратные уравнения. |
| 2 |
|
|
|
| 2 | Теорема Виета. Уравнения, содержащие переменную под знаком модуля. Посторонние корни. |
| 2 |
|
|
|
| 3 | Уравнения с переменной в знаменателе. Область определения уравнения. |
| 2 |
|
|
|
| 4 | Рациональные уравнения. Решение уравнения р(х)= 0 методом: разложения на множители; введения новой переменной. Биквадратное уравнения. Решение задач с помощью составляющих уравнений и систем уравнений. |
| 2 |
|
|
|
| 5 | Иррациональные уравнения. Показательные уравнения. Логарифмические уравнения. Тригонометрические уравнения. |
| 2 |
|
|
|
| 6 | Система уравнений. Уравнения с двумя переменными. Логарифмические неравенства. Показательные неравенства. Тригонометрические неравенства. |
| 2 |
|
|
|
| Практическая работа |
|
|
|
|
|
| 1 | Решение квадратных уравнений |
|
| 2 |
|
|
| 2 | Решение неполных квадратных уравнений |
|
| 2 |
|
|
| 3 | Решение биквадратных, трехчленных уравнений. |
|
| 2 |
|
|
| 4 | Решение рациональных и дробно-рациональных уравнений методом ведения новой переменной. |
|
| 2 |
|
|
| 5 | Решить иррациональное уравнение. |
|
| 2 |
|
|
| 6 | Решить систему уравнений. |
|
| 2 |
|
|
| 7 | Решить линейные неравенства. |
|
| 2 |
|
|
| 8 | Решить систему неравенств, приводимые к линейным и методом интервалов. |
|
| 2 |
|
|
| 9 | Решение показательных, логарифмических неравенств. |
|
| 1 |
|
|
| 10 | Контрольная работа к разделу «Уравнения и неравенства». |
|
| 1 |
|
|
| Самостоятельная работа |
|
|
|
|
|
| 1 | Решение задач методом разложения на множители. |
|
|
| 2 |
|
| 2 | Решите иррациональные уравнения. |
|
|
| 2 |
|
| 3 | Решите показательные уравнения. Решите показательные неравенства. |
|
|
| 2 |
|
| 4 | Решить систему уравнений с двумя переменными. |
|
|
| 2 |
|
| 5 | Решите систему тригонометрических уравнений. |
|
|
| 2 |
|
| 6 | Решите систему показательных уравнений. |
|
|
| 2 |
|
| 7 | Решите систему логарифмических уравнений. |
|
|
| 2 |
|
| 8 | Задачи на составление уравнений
|
|
|
| 1 |
|
| Раздел 3. Комбинаторика, статистика и теория вероятности. |
| Тема 3.1. Элементы комбинаторики.
|
Содержание учебного материала | 6 | 2 | 4 | 3 |
|
| 1 | Основные понятия комбинаторики. Элементы комбинаторики. Задачи на перебор вариантов. Задачи на подсчет числа размещений, перестановок, сочетаний. Свойства биноминальных коэффициентов. Формула бинома Ньютона. Треугольник Паскаля. |
| 2 |
|
|
|
| Практическая работа |
|
| 1 | Решение комбинаторных задач методом: перебор вариантов. |
|
| 2 |
|
|
| 2 | Решение комбинаторных задач методом: правило умножения. |
|
| 1 |
|
|
| 3 | Контрольная работа. |
|
| 1 |
|
|
| Самостоятельная работа |
|
| 1 | Придумать задачу на комбинаторное правило умножения и оформить ее на альбомном листе. |
|
|
| 2 |
|
| 2 | Доклад на тему «Комбинаторика в профессии сварщик» |
|
|
| 1 |
|
| Тема 3.2. Элементы теории вероятности. Элементы математической статистики. | Содержание учебного материала | 6 | 2 | 4 | 3 |
|
| 1 | Предмет и задачи математической статистики. Определение вероятности: испытание, событие, случайные величины. Вероятность событий, действие над событиями. Число сочетаний, размещений и перестановок. |
| 2 |
|
|
|
| Практическая работа. |
|
| 1 | Решение задач по теории вероятности. |
|
| 2 |
|
|
| 2 | Решение задач по статистике. |
|
| 1 |
|
|
| 3 | Контрольная работа |
|
| 1 |
|
|
| Самостоятельная работа |
|
| 1 | Изучить изобретение греческого скульптора Фидия. |
|
|
| 2 |
|
| 2 | Доклад на тему «Статистические данные о профессии сварщик в Горнозаводске» |
|
|
| 1 |
|
| Раздел 4. Геометрия. |
| Тема 4.1. Координаты и векторы. |
Содержание учебного материала |
26 |
10 |
16 |
13 |
|
| 1 | Декардовые координаты на плоскости и в пространстве. Координаты середины отрезка, расстояние между точками. |
| 2 |
|
|
|
| 2 | Уравнения фигур. |
| 2 |
|
|
|
| 3 | Векторы и операции с ними. Понятие векторы. Равенство векторов. Сложение векторов. Правило параллелепипеда сложения векторов. |
| 2 |
|
|
|
| 4 | Разность векторов. Умножение вектора на число. Скалярное произведение векторов. Разложение вектора на составляющие. |
| 2 |
|
|
|
| 5 | Координаты вектора. |
| 2 |
|
|
|
| Практическая работа |
|
| 1 | Вычисления расстояний между двумя точками. |
|
| 2 |
|
|
| 2 | Вычисление абсолютной величины вектора. |
|
| 2 |
|
|
| 3 | Вычисления скалярного произведения векторов. |
|
| 2 |
|
|
| 4 | Вычисления угла между векторами. |
|
| 2 |
|
|
| 5 | Вычислить вектор и его абсолютную величину. |
|
| 2 |
|
|
| 6 | Вычислить вектор на число. |
|
| 2 |
|
|
| 7 | Вычислить координаты векторов. |
|
| 2 |
|
|
| 8 | Составить уравнение фигур. |
|
| 1 |
|
|
| 9 | Контрольная работа |
|
| 1 |
|
|
| Самостоятельная работа |
|
| 1 | Изучить «прямоугольный базис» |
|
|
| 2 |
|
| 2 | Вычислить координаты середины отрезков. |
|
|
| 2 |
|
| 3 | Вычислить расстояние между точками. |
|
|
| 2 |
|
| 4 | Написать уравнение окружности и сферы, прямой и плоскости. |
|
|
| 2 |
|
| 5 | Выполнить тест по теории: «Векторы». |
|
|
| 2 |
|
| 6 | Доказать признак перпендикулярности векторов. |
|
|
| 2 |
|
| 7 | На координатной плоскости начертить деталь с размерами 1 : 10 |
|
|
| 1 |
|
| Тема 4.2. Прямые и плоскости в пространстве. | Содержание учебного материала | 10 | 4 | 6 | 5 |
|
| 1 | Перпендикулярность прямой и плоскости. Перпендикулярность плоскостей, параллельность плоскостей. |
| 2 |
|
|
|
| 2 | Параллельность прямой и плоскости. Пересекающиеся плоскости. Геометрическое преобразование фигур. |
| 2 |
|
|
|
| Практическая работа |
|
| 1 | Решения задач с доказательствами. |
|
| 2 |
|
|
| 2 | Решение задач «Угол между прямыми» |
|
| 1 |
|
|
| 3 | Решение задач «Угол между прямой и плоскостью». Решение задач «Угол между плоскостями». |
|
| 2 |
|
|
| 5 | Контрольная работа |
|
| 1 |
|
|
| Самостоятельная работа |
|
| 1 | Выполнить опорный конспект по теме: «Параллельность прямых и плоскостей», «Перпендикулярность прямых и плоскостей», «Перпендикулярность плоскостей». |
|
|
| 2 |
|
| 2 | Выполнить опорный конспект «Введение в стереометрию. Аксиомы. Следствия». |
|
|
| 2 |
|
| 3 | Зачет по теории: «Перпендикулярность прямых и плоскостей», «Перпендикулярность плоскостей, двугранный угол». «Параллельность прямых и плоскостей». Задачи на тему вертикальная и горизонтальная сварка |
|
|
| 1 |
|
| Тема 4.3. Многогранники | Содержание учебного материала | 30 | 12 | 18 | 15 |
|
| 1 | Вершины, ребра, грани многогранника. Развертка. |
| 2 |
|
|
|
| 2 | Многогранные углы. Выпуклые многогранники. Теорема Эйлера. |
| 2 |
|
|
|
| 3 | Призма. Прямая и наклонная призма. Правильная призма. |
| 2 |
|
|
|
| 4 | Параллелепипед. Куб. Пирамида. Правильная пирамида. Усеченная пирамида. Тетраэдр. |
| 2 |
|
|
|
| 5 | Симметрии в кубе, в параллелепипеде, в призме и пирамиде. Представление о правильных многогранниках. |
| 2 |
|
|
|
| 6 | Сечение куба, призмы, пирамиды. |
| 2 |
|
|
|
| Практическая работа |
|
| 1 | Определить диагонали параллелепипеда. |
|
| 2 |
|
|
| 2 | Определить ребро куба. |
|
| 2 |
|
|
| 3 | Определить высоту пирамиды. |
|
| 2 |
|
|
| 4 | Определить боковые ребра пирамиды. |
|
| 2 |
|
|
| 5 | Определить грани геометрических фигур. |
|
| 2 |
|
|
| 6 | Построить сечение пирамиды. |
|
| 2 |
|
|
| 7 | Построить сечение параллелепипеда, куба. |
|
| 2 |
|
|
| 8 | Построить сечение призмы. |
|
| 2 |
|
|
| 9 | Построить сечение усеченных фигур. |
|
| 1 |
|
|
| 10 | Контрольная работа |
|
| 1 |
|
|
| Самостоятельная работа |
|
| 1 | Зачет по теории: «Многогранники» |
|
|
| 2 |
|
| 2 | Выполнить развертку призмы, куба. |
|
|
| 2 |
|
| 3 | Выполнить развертку пирамиды, параллелепипеда. |
|
|
| 2 |
|
| 4 | Выполнить развертку наклонной призмы. |
|
|
| 2 |
|
| 5 | Реферат: «Открытие Леонарда Эйлера». |
|
|
| 2 |
|
| 6 | Выполнить развертку любого правильного многогранника. |
|
|
| 2 |
|
| 7 | Изучить тему: «Триангуляция многоугольников и многогранников». |
|
|
| 2 |
|
| 8 | Определить количество материала, необходимого для изготовления многогранников (пирамида, призма, куб …)
|
|
|
| 1 |
|
| Тема 4.4. Тела и поверхности вращения. | Содержание учебного материала | 22 | 6 | 16 | 11 |
|
| 1 | Понятие о поверхностях и телах вращения. Цилиндр. |
| 2 |
|
|
|
| 2 | Конус. Усеченный конус. |
| 2 |
|
|
|
| 3 | Осевые сечение и сечения, параллельные основанию. |
| 1 |
|
|
|
| 4 | Шар. Части шара и сферы. |
| 1 |
|
|
|
| Практическая работа |
|
| 1 | Выполнить развертку цилиндра. |
|
| 2 |
|
|
| 2 | Выполнить развертку конуса, усеченного конуса. |
|
| 2 |
|
|
| 3 | Выполнить развертку шарового сегмента. |
|
| 2 |
|
|
| 4 | Выполнить развертку шарового сектора. |
|
| 2 |
|
|
| 5 | Вычислить площадь развертки цилиндра. |
|
| 2 |
|
|
| 6 | Вычислить площадь развертки конуса. |
|
| 2 |
|
|
| 7 | Вычислить площадь развертки частей шара. |
|
| 2 |
|
|
| 8 | Контрольная работа |
|
| 2 |
|
|
| Самостоятельная работа |
|
| 1 | Зачет по теории: «Тела вращения». |
|
|
| 2 |
|
| 2 | Определить радиус у тел вращения. |
|
|
| 2 |
|
| 3 | Определить образующую у тел вращения. |
|
|
| 2 |
|
| 4 | Снять замеры развертки цилиндра. |
|
|
| 2 |
|
|
| 5 | Снять замеры развертки конуса. |
|
|
| 2 |
|
| 6 | Площади фигур |
|
|
| 1 |
|
| Тема 4.5. Измерения в геометрии. | Содержание учебного материала | 16 | 4 | 12 | 8 |
|
| 1 | Понятие объема фигур. Объем призмы. Объем пирамиды. Объем усеченной пирамиды. |
| 1 |
|
|
|
| 2 | Объем цилиндра. Объем конуса. Объем шара. Объем частей шара. |
| 2 |
|
|
|
| 3 | Площади поверхностей круглых фигур: цилиндра, конуса. |
| 1 |
|
|
|
| Практическая работа |
|
| 1 | Решение задач: определить поверхность параллелепипеда по трем измерениям. |
|
| 2 |
|
|
| 2 | Решение задач: определить площадь диагонального сечения. |
|
| 2 |
|
|
| 3 | Решение задач: определить объем геометрических фигур. |
|
| 2 |
|
|
| 4 | Решение задач: определить площадь основания пирамиды. |
|
| 2 |
|
|
| 5 | Решение задач: определить объем геометрических фигур. |
|
| 2 |
|
|
| 6 | Контрольная работа |
|
| 2 |
|
|
| Самостоятельная работа |
|
| 1 | Изучить «Вписанные многоугольники» |
|
|
| 2 |
|
| 2 | Изучить «Описанные многоугольники» |
|
|
| 2 |
|
| 3 | Изучить «Вневписанная окружность» |
|
|
| 2 |
|
| 4 | Задачи на нахождение площади.
|
|
|
| 2 |
|
Реализация учебной дисциплины требует наличия учебного кабинета математики; мастерских не требует; лабораторий не требует.
Оборудование учебного кабинета: рабочая доска, наглядные пособия (учебники, разных типов, опорные конспекты, карточки).
Оборудование мастерской и рабочих мест мастерской не предусмотрено.
Оборудование лабораторий и рабочих мест лабораторий не предусмотрено.
1. Ш.А. Алимов и др. Алгебра и начала анализа 10 (11) кл. – М., 2000.
2. Л.С. Атанасян и др. Геометрия. 10 (11) кл. – М., 2000.
3. М.И. Башмаков. Алгебра и начала математического анализа (базовый уровень). 10 кл. – М., 2005.
4. М.И. Башмаков. Математика (базовый уровень). 10-11 кл. – М., 2005.
5. А.Н. Колмогоров и др. Алгебра и начала анализа. 10 (11) кл. – М., 2000.

 Получите свидетельство
Получите свидетельство Вход
Вход











 Программа по математике (60.72 КB)
Программа по математике (60.72 КB)
 0
0 542
542 40
40 Нравится
0
Нравится
0



