Применение иерархических систем

Применение иерархических систем

для структурного анализа

Суровцева Н.Н., Клейменов В.Ф.

Иркутский национальный исследовательский технический университет,

Иркутск, Россия

Одним из инструментариев в теории информационных систем являются иерархические информационные системы. Категория пожилых людей имеет сложную структуру, разбивается на большое количество групп, как пересекающихся между собой, так и не имеющих пересечения. При этом многим группам присущи одинаковые функции, возможно, с различными значениями (см., например [1, 2]). Так как страты с течением времени могут изменяться, появляются новые или исчезают уже имеющиеся, то исходную решетку полезно представлять себе потенциально бесконечной, а само множество страт в виде иерархической системы. Дадим необходимые определения.

Определение 1. Упорядоченным множеством L называется множество, на котором определено бинарное отношение x≤y, удовлетворяющее для любых элементов x, y, z из L следующим условиям: 1. x≤x (рефлексивность), 2. если x≤y и y≤x, то x=y (антисимметричность), 3. если x≤y и y≤z, то x≤z (транзитивность). Элемент a упорядоченного множества L называется точной верхней (нижней) гранью элементов x и y этого множества, если x≤a, y≤a (a≤x, a≤y) и для любого b, такого, что x≤b, y≤b (b≤x, b≤y) имеет место, a≤b (b≤a). Точная верхняя грань элементов x, y обозначается x y, а точная нижняя x y. Упорядоченное множество L, в котором для любых элементов этого множества определена точная верхняя и точная нижняя грань называется решеткой.

Определение 2. Подмножество I решетки L будем называть иерархией, если для любых двух элементов множества I определена их точная верхняя грань.

Элементы иерархических систем будем называть стратами. Для каждой страты могут быть дополнительно определены некоторые свойства или условия (например, численность, размер выплаты и т.д.).

Рассмотрим пример иерархической системы для социальной группы пожилых людей. При этом такое свойство, как численность страт будем рассматривать по доступным нам данным (2009 год), а динамика изменения численности страт, изменения различных выплат будет рассмотрена в §4.

Пример 1. Обозначим переменными S_i следующие страты: S₀ – Пенсионеры, S₁ – Инвалиды ВОВ, S₂ – Ветераны ВОВ (кроме тружеников тыла), S₃ – Вдовы ИВОВ, УВОВ, S₄ – Труженики тыла, S₅ – Ветераны труда, S₆ – Реабилитированные лица и лица признанные пострадавшие от политических репрессий, S₇ – Пенсионеры не относящиеся к льготным категориям.

Используя операции объединения и пересечения, из исходных страт можно построить более сложную иерархическую систему. Например, S₈ включает в себя группу пенсионеров имеющие категории Ветераны ВОВ, Вдовы ИВОВ, УВОВ; в S₁₁Вдовы ИВОВ, УВОВ, Труженики тыла, Ветеран труда; в S₁₅ входят категории Ветераны труда, реабилитированные лица и лица признанные пострадавшие от политических репрессий. Таким образом, получаем следующую иерархию.

S₀

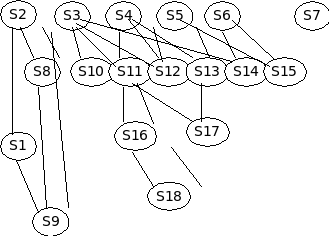
Страты S_1,…,S₁₈ удовлетворяют следующим соотношениям:

S₁ S₂, S₁∩S₃≠Ø, S₃∩S₂≠Ø, S₂∩S₄≠Ø, S₄∩S₃≠Ø, S₄∩S₅≠Ø, S₆∩S_i≠Ø,

S₇∩S_i≠Ø, S₈=S₂∩S₃, S₁₀ S₃, S₁₆=S₁₁∩S_12.

Следующие два определения понадобятся нам для дальнейших исследований.

Определение 3. Два эквивалентных условия для элементов x, y, z решетки L называются дистрибутивностью:

1. x (y z) = (x y) (x z)

2. x (y z)=(x y) (x z)

Определение 4. Для элементов x, y, z решетки L условие, определенное следующим образом: если x≤z, то x (y z)= (x y) z, называется модулярностью.

Если условия 1, 2 выполняются для любых элементов x, y, z решетки L, то эта решетка называется дистрибутивной, а если для любых элементов x, y, z выполняется условие модулярности, то решетка называется модулярной [3]. Любая дистрибутивная решетка модулярна, но обратное не верно. Кроме того, существуют решетки для которых не выполняется условие модулярности, а значит и дистрибутивности. В иерархических системах существуют страты x, y, z, для которых не выполняется условия 1, 2 и условие модулярности, то есть справедливо следующее утверждение.

Утверждение 1. Существует немодулярная решетка, содержащаяся в построенной выше иерархической системе.

Доказательство. Обозначим через S₀ - страту пожилых людей, являющихся либо УВОВ, либо инвалидами 1 группы, S₁ – страту пожилых людей являющихся УВОВ, S₂ – страту пожилых людей инвалиды 1 группы, S₃ – страту пожилых людей ИВОВ, S₄ – страту пожилых инвалидов 1 группы УВОВ. Тогда выполняются следующие равенства: S₀ =S₁ S₂, S₃ ≤ S₁, S₄ =S₂ S₃.

Докажем, что для элементов S₁, S₂, S₃ не выполняется тождество модулярности. Действительно, S₃≤S₁, рассмотрим элемент S₃ (S₂ S₁). Так как S₂ S₁= S₄, а S₃ S₄=S₃, то S₃ (S₂ S₁)=S₃. С другой стороны, вычислим элемент (S₃ S₂) S₁. Так как S₃ S₂= S₀, а S₀ S₁= S₁, то (S₃ S₂) S₁=S₁. Таким образом, S₃ (S₂ S₁)≠(S₃ S₂) S₁, более точно S₃ (S₂ S₁)S₃ S₂) S₁, что и доказывает немодулярность построенной решетки.

Замечание. Отметим, что внеся даже небольшие изменения в построении примера из утверждения 1, можно получить модулярную решетку.

Пример 2. Пусть S₀ – страта пожилых людей являющихся либо инвалидами, либо людьми имеющими высшее образование, S₁ – пожилые люди инвалиды, S₂ – пожилые люди с высшим образованием, S₃ – пожилые люди инвалиды 1 группы, S₄ – пожилые инвалиды с высшим образованием, S₅ – пожилые инвалиды 1 группы с высшим образованием. Тогда S₀=S₁ S₂, S₃≤S_1, S₄=S₁ S₂, S₅=S₂ S₃. Рассмотрим элемент S₃ (S₂ S₁), получим S₃ S₂= S₀ и S₀ S₁= S₁. Таким образом, S₃ (S₂ S₁)=(S₃ S₂) S₁ и модулярность, для элементов S₁, S₂, S₃ выполняется.

Можно отметить, что большинство подрешеток в иерархии страт все - таки удовлетворяют условию модулярности. Более того, в любой иерархии можно построить подрешетку удовлетворяющую условию не только модулярности, но и дистрибутивности.

Утверждение 2. В любой иерархии существует последовательность страт S_i , S_i , … S_i , которые образуют дистрибутивную подрешетку.

Доказательство. Определим страту S_i следующим образом. S_i - страта пожилых людей, возраст которых не больше I лет. Тогда получим последовательность страт S_i S_i+1S_i+2S_i+k , где i – возраст самых молодых людей, i+k - возраст самых старых людей. Данная последовательность является линейно упорядоченной и, по утверждению леммы из [1] стр. 25, является дистрибутивной решеткой.

Список литературы

1. М. Месарович, Д. Мако Д, Такахара И., Теория иерархических многоуровневых систем «Мир», М., 1973г., 344с.

2. Г. Биркгоф., Теория решеток, «Наука», М., 1984г., 566с.

3. Суровцева Н.Н., Клейменов В.Ф. О модулярных решетках в иерархии страт // Успехи современного естествознания. - 2010. - № 9. - С. 204-205.