Разработка урока «Применение уравнения окружности к решению задач»
Тема урока: Применение уравнения окружности к решению задач
Цели:
Образовательные: Показать связь между алгеброй и геометрией.
Уметь:
– Находить уравнение окружности ; приводить формулу к стандартному виду.
– Применять современные ИКТ для оформления результатов исследования.
– В комплексе применять полученные знания
Воспитательные: Формирование критического мышления и навыков работы в группе.
Развивающие: Приобретение навыков работы с большими объёмами информации.
Уметь:
–Видеть проблему и наметить пути её решения.
–Кратко излагать свои мысли устно и письменно.
Тип урока: Обобщение и оценка знаний.
Оборудование: ПК , мультимедийный проектор, экран, оценочные листы для учителя и учащихся.
План урока:
1. Вступительное слово учителя – 3 мин.
2. Актуализация знаний учащихся (общеклассная дискуссия), составления алгоритма приведения уравнения окружности к стандартному виду – 10 мин.
3. Самостоятельная работа обучающего характера – 7 мин.
4. Закрепление полученного алгоритма. Рассматривается на примере задачи Аполлония Пергского, (260-170 гг. до н.э.), объяснение учителя – 7 мин.
5. Защита творческой работы учащихся теме: «Уравнение окружности. Загадочная формула». Обсуждение – 15 мин.
6. Подведение итогов. Задание на дом – 3 мин.
Ход урока:
1. Вступительное слово
На последних уроках геометрии мы познакомились с еще одним способом решения задач методом координат.
Алгебра и геометрия, которые сейчас большинство школьников воспринимают как совершенно разные науки, на самом деле очень близки. С помощью метода координат можно было бы изложить весь курс геометрии используя только числа и алгебраические операции.
Задавая фигуры уравнением и выражая в координатах геометрические соотношения, мы применяем алгебру к геометрии. Так мы поступили, когда выразили через координаты основную геометрическую величину – расстояние между точками, а затем, когда вывели уравнение окружности и прямой.
Пользуясь координатами, можно истолковывать уравнения и неравенства геометрически и таким образом применять геометрию к алгебре и анализу. Графическое изображение функций – первый пример такого применения метода координат.
Метод координат в соединении с алгеброй составляет раздел геометрии, называемый аналитической геометрией.
Сегодня мы поговорим об уравнении окружности и проследим, как алгебра помогает в решении геометрических задач и наоборот.
2. Актуализация знаний
На доске написаны уравнения. Какие фигуры они задают? Общеклассная дискуссия сопровождается презентацией (Приложение 2. – «Применение уравнения окружности к решению задач»).
Слайд 3 презентации
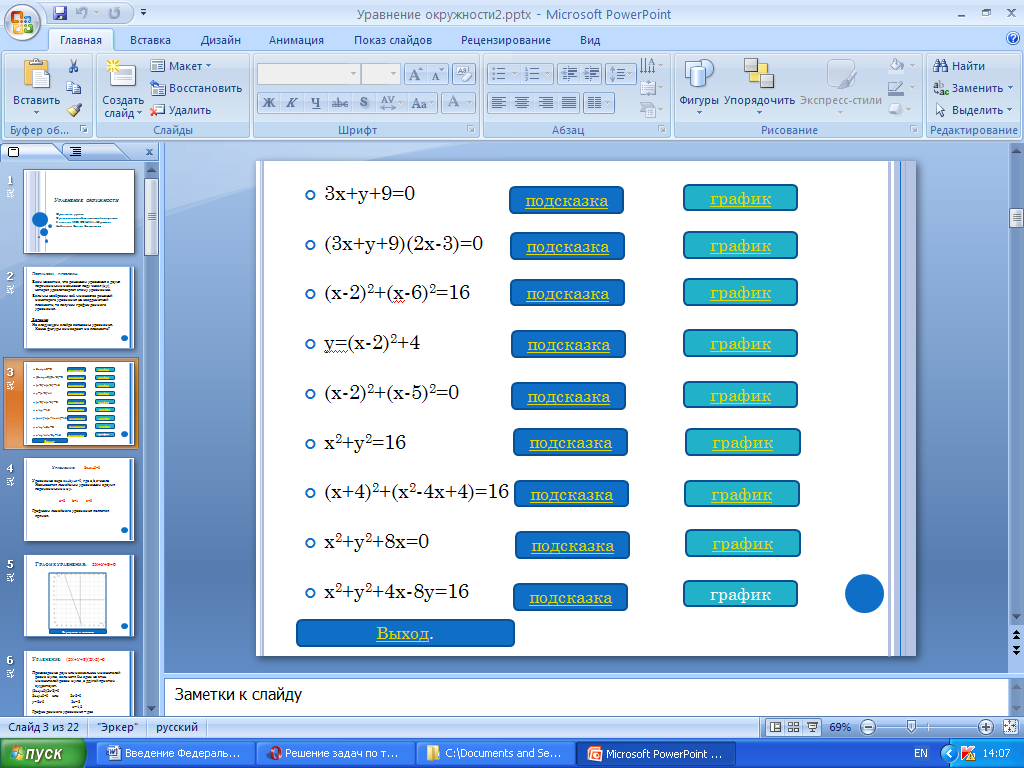
3. Закрепление
Самостоятельная работа, взаимопроверка. Правильные ответы записаны на откидной доске.
Карточки для самостоятельной работы
1 вариант
| 2 вариант |
| (Х+5)2+(у-6)2=1 | (Х-9)2+(у-2)2=25 |
| (Х-2)2+(у2-2у+1)=1 | (Х+4)2+(у2-6у+9)=25 |
| Х2+у2-6х+2у=2 | Х2+4х+у2-4у=2 |
Задание: выясните, будет ли данные уравнения задавать окружность, если да, то укажите радиус и координаты центра.
4.Следующую задачу решает учитель
Задача: Что представляет собой множество точек плоскости, отношение расстояний от которых до двух данных точек есть величина постоянная?
Решение: Впервые эту задачу сформулировал и решил Аполлоний Пергский, (260-170 гг. до н.э.)
Решение получилось очень сложное – поскольку применены геометрические приемы. Однако в работах французского математика Рене Декарта эта задача решена более элегантно. Декарт применил метод координат.
Я предлагаю посмотреть на это решение. Итак, пусть даны две точки ,А и В и некоторое положительное число k, равное отношению расстояний до точки М.
1случай. Если k=1,тогда множество точек М есть серединный перпендикуляр к отрезку АВ.
2 случай. Пусть k целое не отрицательное число не равное 1
Для удобства решения возьмем k=2 , т.е. МА: МВ=2.
Введем систему прямоугольных координат. Совместим начало отсчета с точкой В. В качестве положительной полуоси x возьмем луч ВА. (рис.2)
Тогда получим следующие координаты точек: В(0,0), А(a,0), М(x,y). Пусть a=3 опять для простоты рассуждений.
Тогда, пользуясь формулами расстояния между двумя точками, запишем:
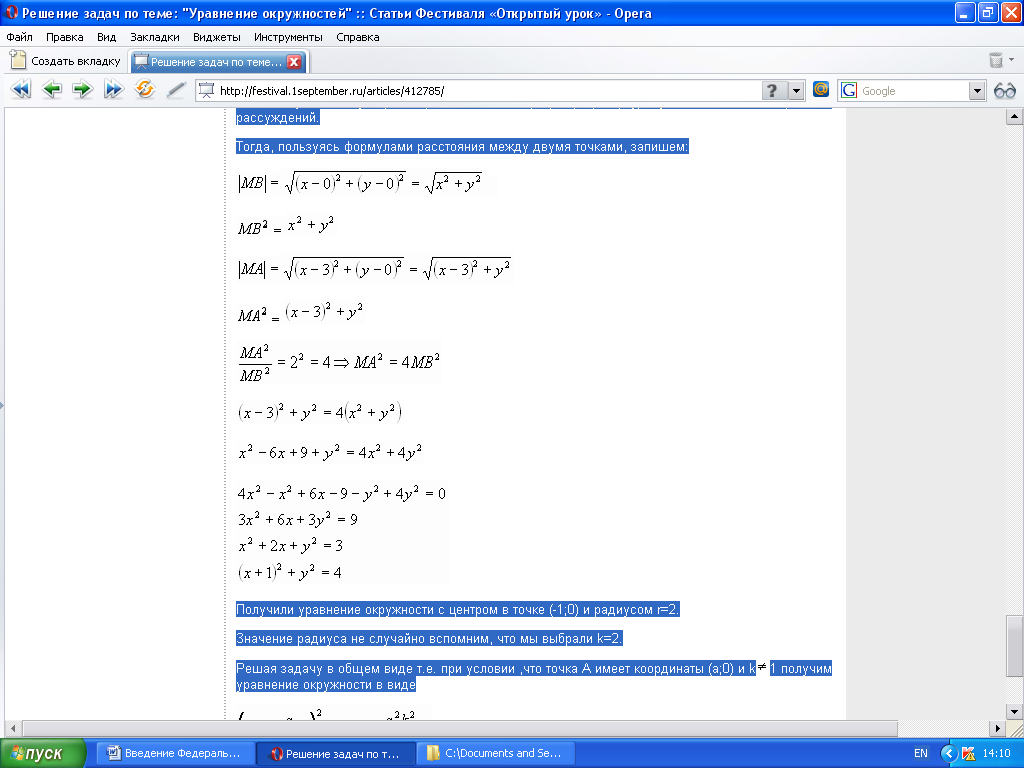
Получили уравнение окружности с центром в точке (-1;0) и радиусом r=2.
Значение радиуса не случайно вспомним, что мы выбрали k=2.
Решая задачу в общем виде т.е. при условии ,что точка А имеет координаты (a;0) и k≠1 получим уравнение окружности в виде:
Такая окружность называется окружностью Апполония.
Окружность Апполония
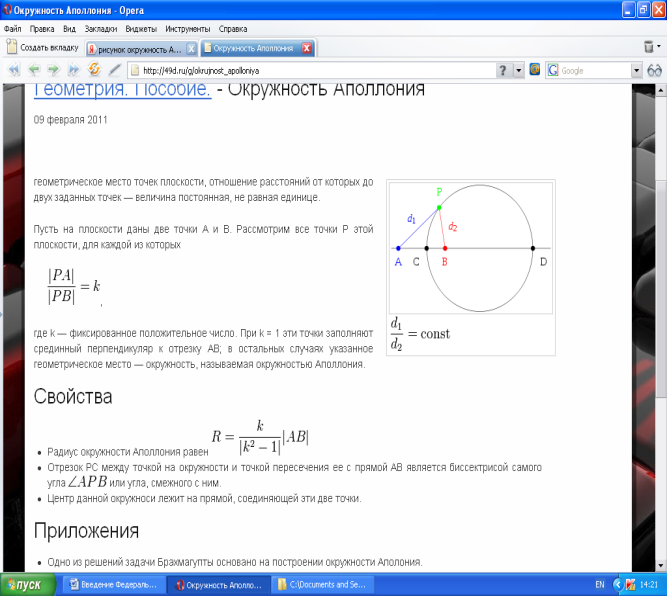
Таким образом, мы решили геометрическую задачу алгебраическим методом.
5. Защита проекта
За неделю до урока группа учащихся получает индивидуальное задание выполнить проект: «Уравнение окружности. Загадочная формула».
Требования к презентации
1. Общие:
1.1. Количество слайдов – не менее 6, не более 10
1.2. Обязательные слайды: тема и авторы; цели; выводы; используемые источники информации (не менее 3)
2. Содержание:
2.1. Факты изложены чётко, кратко и доступно.
2.2. Наличие целей работы и соответствующих целям выводов
3. Оформление:
3.1. Единая цветовая схема.
3.2. Размер шрифта: для заголовка–не менее 36, для текста –18.
3.3. Количество эффектов анимации – не более 3 на слайд.
3.4. Использование картинок, фотографий, видео, а также таблиц, схем и диаграмм.
Карточка с предварительным заданием группе
Предварительное задание группе:
| Тема проекта: «Уравнение окружности. Загадочная формула». |
| Примерное содержание проекта: |
Окружность как модель устройства мира. Решение алгебраической задачи с помощью геометрии на примере задачи Германа Минковского (1864-1909 г). Применение алгебраических и геометрических методов решения задач в жизненных ситуациях. |
| Возможные информационные источники: |
Математический энциклопедический словарь. Аналитическая геометрия. М., «Советская энциклопедия»,1988 Сикорский К. П.Дополнительные главы по курсу математики. М.,Просвещение,1969 Сайт «Устье Речи», http://ustierechi.ucoz.ru/publ/14-1-0-169 Сайт bestreferat.ru http://www.bestreferat.ru/referat-135774.html |
| Результаты своей работы представить в виде презентации, выполненной в Power Point. |
Сейчас рассмотрим обратный вариант – решение алгебраической задачи с помощью геометрии. На уроке будет представлена защита творческой работы, которую выполнила группа учащихся класса. После презентации 2–3 минуты даётся на обсуждение.
Схема обсуждения :
– Перечислить три наиболее сильные стороны представленной презентации.
– Перечислить два момента, требующих доработки.
– Внести свои предложения по усовершенствованию проекта (если такие есть).
– Сделать итоговый вывод и выставить общий балл за выступление на основании листов оценивания.
Критерии оценки проекта
1) обоснованность актуальности темы проекта и предлагаемых решений;
2) объем, полнота разработок, самостоятельность, законченность;
3) уровень творчества, оригинальность раскрытия темы;
4) дизайн, стиль, соответствие стандартным требованиям, структура текста, качество схем, рисунков, диаграмм, анимации и др.;
5) качество доклада;
6) проявление глубины и широты знаний по излагаемой теме.
Лист оценивания презентаций
| Оценивайте каждый критерий по 5–ти бальной системе. Сложите баллы в каждой колонке и разделите на 5 (количество критериев), округлите полученный результат до целого числа.
|
| Критерии | Баллы |
Представленные факты точны, полезны и актуальны. |
|
Использована научная терминология |
|
Презентация логично выстроена |
|
В презентации поставлены цели, они достигнуты, сделаны соответствующие выводы. |
|
Использование картинок, видео, звука обосновано, логично, соответствует моменту. |
|
| Сумма баллов |
|
| Оценка |
|
6. Итак, подведём итоги
Судя по содержанию вашей презентации объёму переработанного материала, тема усвоена хорошо. Вы убедились, что в окружающей нас действительности возникает много различных ситуаций, связанных с решением геометрических и задач. Это делает мир вокруг нас красивым и гармоничным.
Результаты вашей работы мы подведём на следующем уроке выведением среднего балла за все этапы работы над проектом.
Подведение итогов. Задание на дом: Повторение материала по теме: «Метод координат в пространстве».


 Получите свидетельство
Получите свидетельство Вход
Вход

















 Применение уравнения окружности к решению задач (конспект) (0.49 MB)
Применение уравнения окружности к решению задач (конспект) (0.49 MB)
 0
0 949
949 91
91 Нравится
0
Нравится
0


