Презентация "Загадочное число ПИ"

Загадочное число

Исследовательская работа

Выполнила

ученица 9 класса

Селянской школы

Нелидовского района

Поликарпова Екатерина

Руководитель: Соловьева Т.А.

ЦЕЛИ И ЗАДАЧИ

Цель:

Расширить свои знания о необычном

математическом числе ПИ.

Задачи:

• Собрать информацию об истории появления

числа ПИ.

2. Рассмотреть интересные факты, связанные

с числом ПИ.

3. Провести мини-исследование о числе ПИ.

Загадочное число

Используется

в математике и в повседневной

жизни.

История числа «ПИ»

• Как утверждают современные ученые, впервые число Пи начали применять в Египте около 1700 года до нашей эры. Оказывается, два понятия - египетские пирамиды и число Пи связаны невидимыми и прочными нитями. Пирамиды строго ориентированы по сторонам света, все их размеры связаны со значением числа Пи с точностью до нескольких знаков после запятой, а главная усыпальница состоит из треугольников, благодаря которым прославился Пифагор.
• Как утверждают современные ученые, впервые число Пи начали применять в Египте около 1700 года до нашей эры.
• Оказывается, два понятия - египетские пирамиды и число Пи связаны невидимыми и прочными нитями.
• Пирамиды строго ориентированы по сторонам света, все их размеры связаны со значением числа Пи с точностью до нескольких знаков после запятой, а главная усыпальница состоит из треугольников, благодаря которым прославился Пифагор.

• Архимед, возможно, первым предложил математический способ вычисления π. Для этого он вписывал в окружность и описывал около неё правильные многоугольники. Принимая диаметр окружности за единицу, Архимед рассматривал периметр вписанного многоугольника как нижнюю оценку длины окружности, а периметр описанного многоугольника как верхнюю оценку. Рассматривая правильный 96-угольник, Архимед получил оценку .

• Около 265 года н. э. математик Лю Хуэй из царства Вэй предоставил простой и точный итеративный алгоритм (англ.) с любой степенью точности. Он самостоятельно провёл вычисление для 3072-угольника и получил приближённое значение для π по следующему принципу:

• Впервые обозначением этого числа греческой буквой π воспользовался британский математик Уильям Джонс (1706), а общепринятым оно стало после работ Леонарда Эйлера. Это обозначение происходит от начальной буквы греческих слов περιφέρεια — окружность, периферия и περίμετρος — периметр.
• Впервые обозначением этого числа греческой буквой π воспользовался британский математик Уильям Джонс (1706), а общепринятым оно стало после работ Леонарда Эйлера. Это обозначение происходит от начальной буквы греческих слов περιφέρεια — окружность, периферия и περίμετρος — периметр.

Трансцендентность

• π — трансцендентное число, это означает, что оно не может быть корнем какого-либо многочлена с целыми коэффициентами. Транцендентность числа π была доказана в 1882 году профессором Кенигсбергского, а позже Мюнхенского университета Линдеманом. Доказательство упростил Феликс Клейн в 1894 году.
• Поскольку в евклидовой геометрии площадь круга и длина окружности являются функциями числа π, то доказательство трансцендентности π положило конец спору о квадратуре круга, длившемуся более 2,5 тысяч лет.

Компьютер и число π.

• 1949 год - 2037 десятичных знаков
• 1958 год - 10000 десятичных знаков
• 1961 год - 100000 десятичных знаков
• 1973 год - 10000000 десятичных знаков
• 1986 год - 29360000 десятичных знаков
• 1987 год - 134217000 десятичных знаков
• 1989 год - 1011196691 десятичный знак
• 1991 год - 2260000000 десятичных знаков
• 1994 год - 4044000000 десятичных знаков
• 1995 год - 4294967286 десятичных знаков
• 1997 год - 51539600000 десятичных знаков
• 1999 год - 206158430000 десятичных знаков.

В 2011 году ученые смогли вычислить значение числа π с точностью в 10 триллионов цифр после запятой!

Применение числа ПИ

В современной математике число ПИ—это не только отношение окружности к диаметру, оно входит в большое число различных формул, в том числе и в формулы неевклидовой геометрии. Число ПИ одна из фундаментальных математических констант. Оно встречается во многих уравнениях различных направлений науки:

• в уравнениях гравитационного поля Эйнштейна;
• в уравнениях, связанных с образованием радуги;
• в уравнениях, описывающих распространение зыби при падении дождевой капли в воду;
• в уравнениях нормального распределения Гаусса;
• в задачах навигации и т.д.

Астрономия. Космонавтика. Архитектура. Строительство. Машиностроение. Навигация. Кораблевождение. Физика. Электроника. Электротехника. Теория вероятностей. Информационные технологии.

Число ПИ в жизни школьника

• Алгебра: - иррациональное и трансцендентное число;
• Тригонометрия: - радианное измерение углов;
• Планиметрия: - длина окружности и её дуги; площадь круга и её частей;
• Стереометрия: - объём шара и частей; - объём цилиндра, конуса и усечённого конуса; - площадь поверхности цилиндра, конуса и сферы;
• Теория вероятностей: - формула Стирлинга для вычисления факториала;
• Физика: - теория относительности; - квантовая механика; - ядерная физика.

Мнемонические правила

Чтобы нам не ошибаться, Надо правильно прочесть: Три, четырнадцать, пятнадцать, Девяносто два и шесть.

Три, четырнадцать, пятнадцать,

Девять, два, шесть, пять, три, пять,

Чтоб наукой заниматься,

Это каждый должен знать.

Памятник числу «пи» на ступенях перед зданием Музея искусств в Сиэтле.

Неофициальный праздник «День числа ПИ» отмечается 14 марта

• Отношение длины берега к расстоянию между истоком и устьем примерно равно 3,14.
• Символ ПИ используется в математических формулах на протяжении 250 лет.
• Самое полезное и самое неуловимое число. В книге «Fractals for the Classroom» говорится: «Число Пи захватывает умы гениев науки и математиков-любителей во всем мире».
• Английский математик Август де Морган назвал как-то «ПИ» «…загадочным числом 3,14159…, которое лезет в дверь, в окно и через крышу».

Интересные факты

Вывод

• π - это одно из множества представителей иррациональных чисел;
• π — математическая константа, выражающая отношение длины окружности к длине её диаметра. Обозначается буквой греческого алфавита π.
• Число π впервые возникло в геометрии как отношение длины окружности к длине её диаметра, однако оно появляется и в других областях математики.
• Число π иррационально и трансцендентно.

Литература:

• Бохан К.А. и др. Курс математического анализа т. II. – М.: Просвещение 1972
• А.В. Жуков «Вездесущее число», «О числе»,
• Кымпан Ф. История числа р. – М.: Наука Гл. ред. Физ.- мат. Лит.,
• Райк А.Е. Очерки по истории математики в древности.
• Звонкин А. Что такое ПИ.
• Калейдоскоп Число ПИ
• Http://ru.wikipedia.org/wiki/ Число_ПИ
• Интернет ресурсы

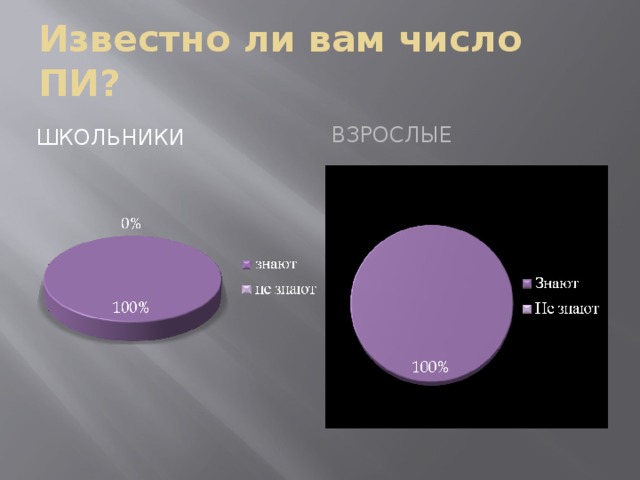
Известно ли вам число ПИ?

Взрослые

Школьники

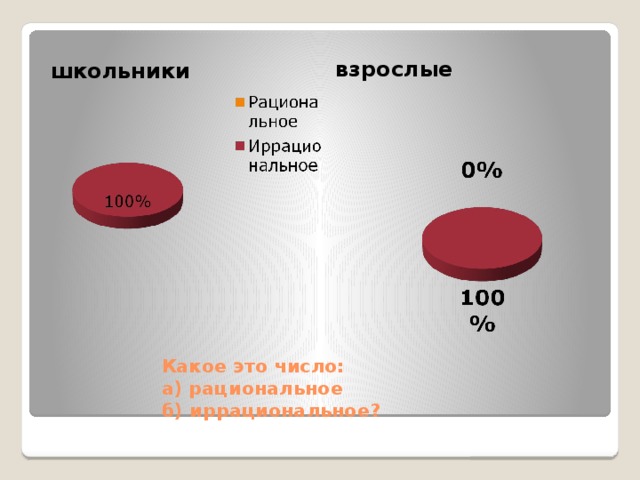
школьники

взрослые

Какое это число: а) рациональное б) иррациональное?

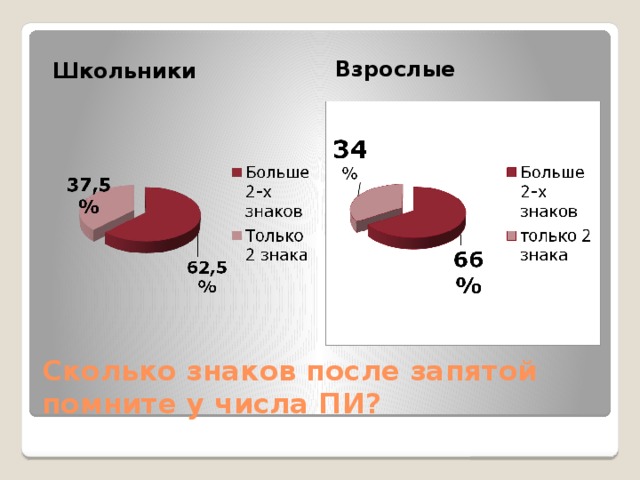
Взрослые

Школьники

Сколько знаков после запятой помните у числа ПИ?

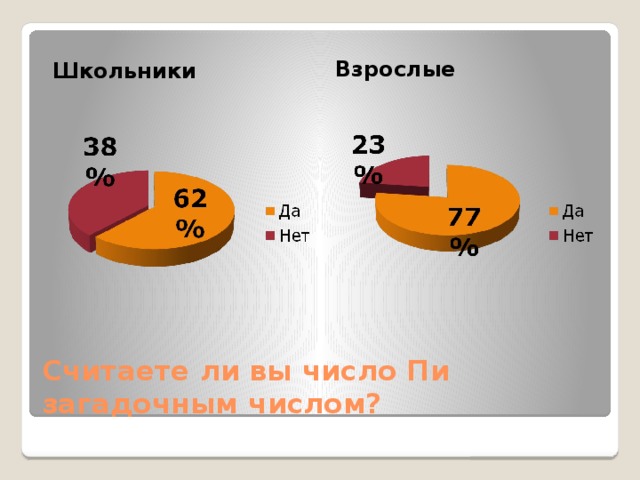
Взрослые

Школьники

Считаете ли вы число Пи загадочным числом?

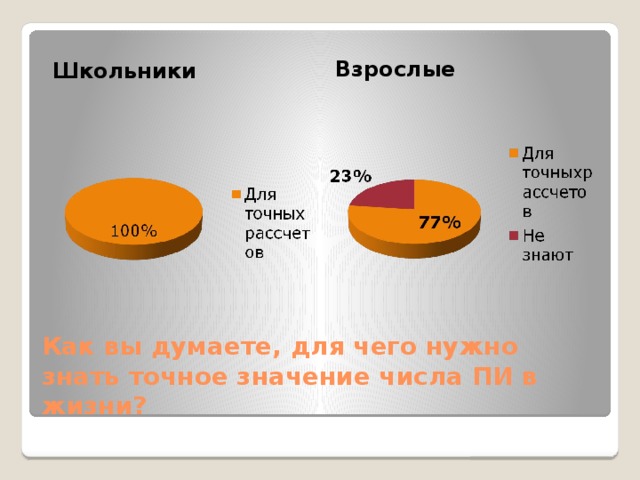
Взрослые

Школьники

Как вы думаете, для чего нужно знать точное значение числа ПИ в жизни?

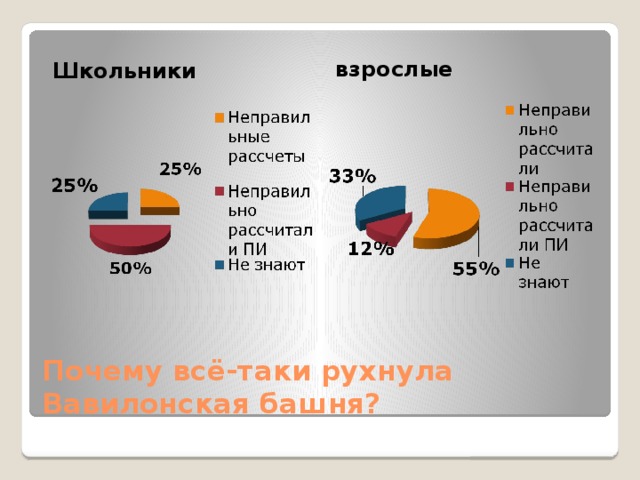
взрослые

Школьники

Почему всё-таки рухнула Вавилонская башня?

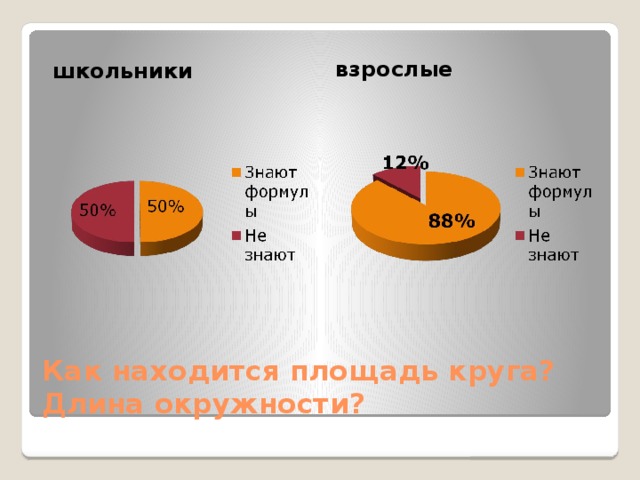
взрослые

школьники

Как находится площадь круга? Длина окружности?

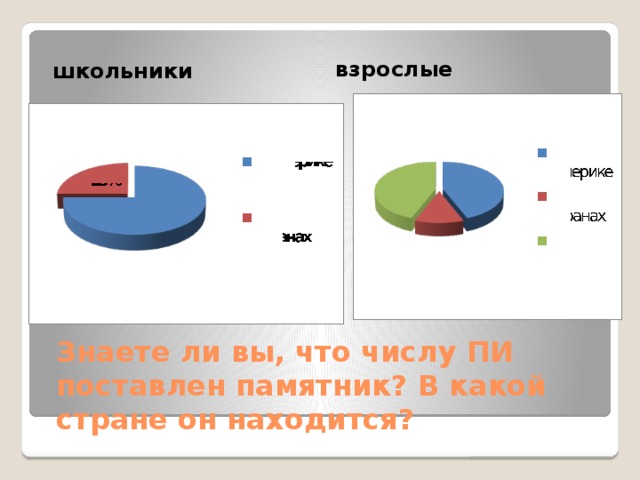
взрослые

школьники

Знаете ли вы, что числу ПИ поставлен памятник? В какой стране он находится?