Получите свидетельство
Вход
«Расстояние от точки до плоскости. Теорема о трех перпендикулярах»
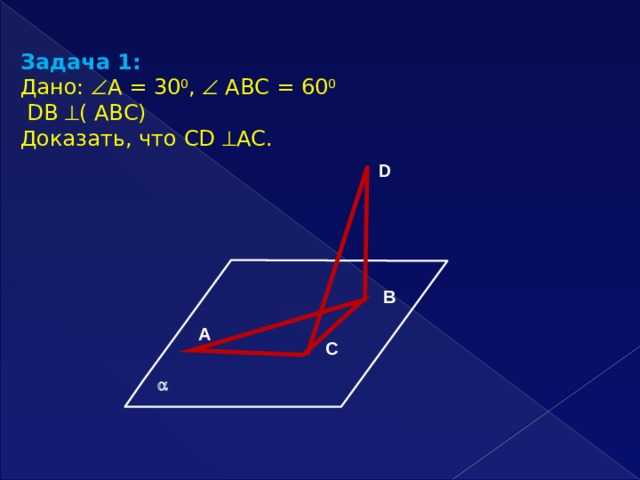
Задача 1:
Дано: А = 30 0 , АВС = 60 0
DВ ( АВС)
Доказать, что СD АС.
D
В
А
С
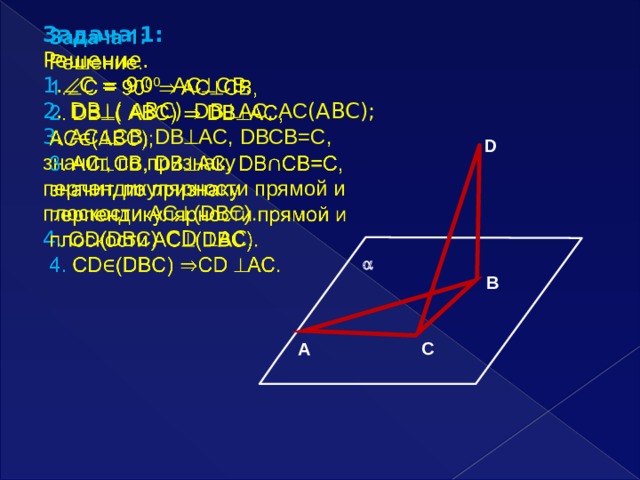
Задача 1:
Решение.
1 . С = 90 0 AC СB,
2 . DВ ( АВС) DВ AC, AC (ABC);
3 . AC СB, DВ AC, DВСB=C, значит, по признаку перпендикулярности прямой и плоскости AC (DBC).
4. СD(DBC) СD АС.
D
В
С
А
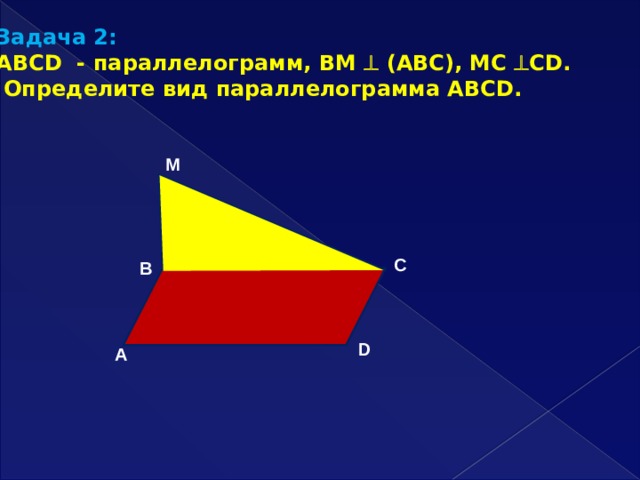
Задача 2:
ABCD - параллелограмм, ВМ (АВС), МС СD.
Определите вид параллелограмма АВСD.
M
C
B
D
A
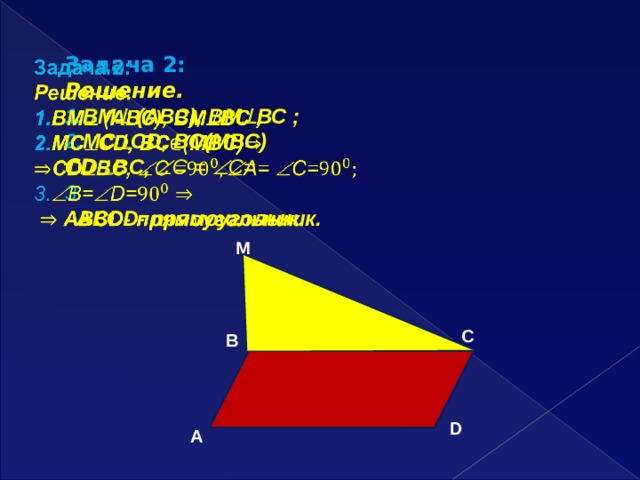
Задача 2:
Решение.
1. ВМ (АВС), ВМ ВС ;
2. МС СD, BC(MBC)
CD BC, C = C=
3.
АВСD- прямоугольник.
M
C
B
D
A
1 . Угол между прямыми равен 90˚. Как называются такие прямые?
Перпендикулярные.
2. Верно ли утверждение: «прямая называется перпендикулярной плоскости, если она перпендикулярна некоторой прямой, лежащей в этой плоскости»
Да.
3. Сформулируйте признак перпендикулярности прямой и плоскости.
Если прямая перпендикулярна двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна к этой плоскости.
4. Как определяется расстояние от точки до прямой на плоскости?
А
- Как длина перпендикуляра, проведенного из точки к данной прямой.
а
Н
М
5. Как называются отрезки АМ, АН?
АМ – наклонная к прямой а;
АН – перпендикуляр, проведенный из точки А к прямой а.
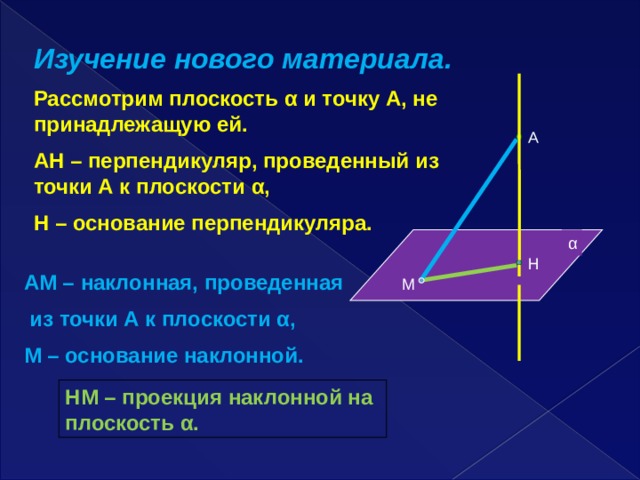
Изучение нового материала.
Рассмотрим плоскость α и точку А, не принадлежащую ей.
АН – перпендикуляр, проведенный из точки А к плоскости α,
Н – основание перпендикуляра.
А
α
Н
АМ – наклонная, проведенная
из точки А к плоскости α,
М – основание наклонной.
М
НМ – проекция наклонной на плоскость α.
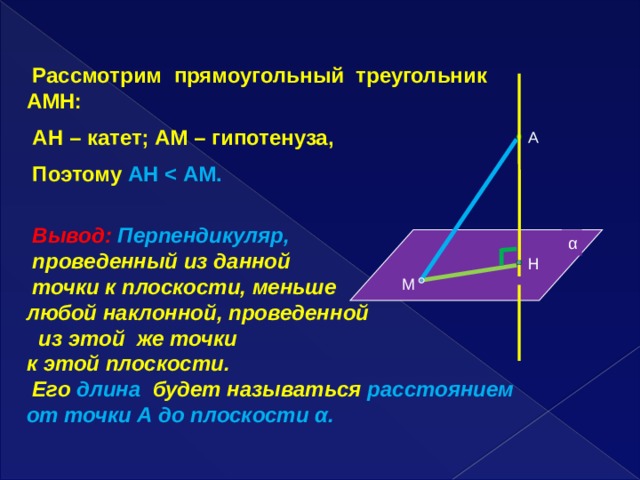
Рассмотрим прямоугольный треугольник АМН:
АН – катет; АМ – гипотенуза,
Поэтому АН
Вывод: Перпендикуляр,
проведенный из данной
точки к плоскости, меньше
любой наклонной, проведенной
из этой же точки
к этой плоскости.
Его длина будет называться расстоянием
от точки А до плоскости α.
А
α
Н
М
Расстояние от лампочки до земли…
6 м
М
а
Если прямая параллельна плоскости, то все точки прямой равноудалены от этой плоскости.
β
N
α
(Доказательство приведено в задаче
№ 144.
Изучить самостоятельно дома)
Расстояние от произвольной точки прямой до плоскости называется расстоянием между прямой и параллельной ей плоскостью.
АА1 = ММ1. Расстоянием между параллельными плоскостями называется расстояние от произвольной точки одной плоскости до другой плоскости. " width="640"
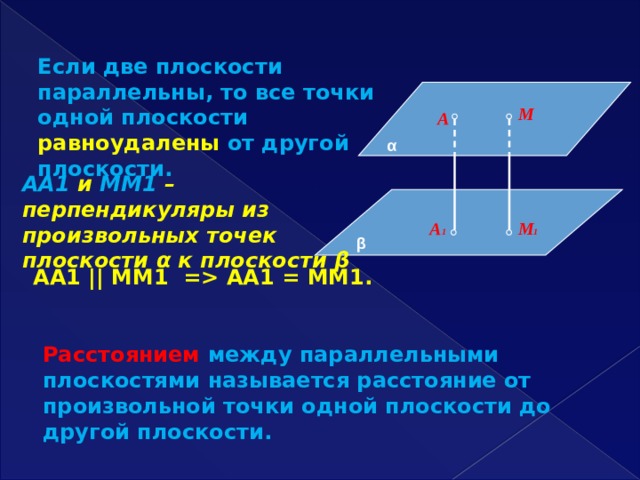
Если две плоскости параллельны, то все точки одной плоскости равноудалены от другой плоскости.
М
А
α
АА1 и ММ1 – перпендикуляры из произвольных точек плоскости α к плоскости β
М 1
А 1
β
АА1 || ММ1 = АА1 = ММ1.
Расстоянием между параллельными плоскостями называется расстояние от произвольной точки одной плоскости до другой плоскости.
М
а
Если две прямые скрещивающиеся, то через каждую из них проходит плоскость, параллельная другой прямой, и притом только одна.
β
в
N
α
Расстояние между одной из скрещивающихся прямых и плоскостью, проходящей через другую прямую параллельно первой, называется расстоянием между скрещивающимися прямыми, MN.
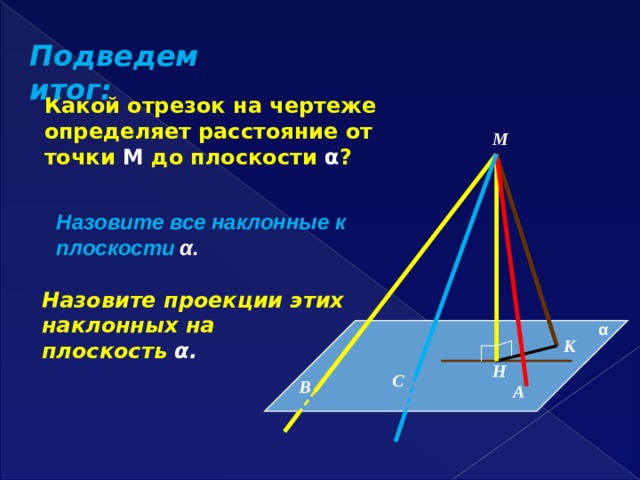
Подведем итог:
Какой отрезок на чертеже определяет расстояние от точки М до плоскости α ?
М
Назовите все наклонные к плоскости α.
Назовите проекции этих наклонных на плоскость α.
α
К
Н
С
В
А
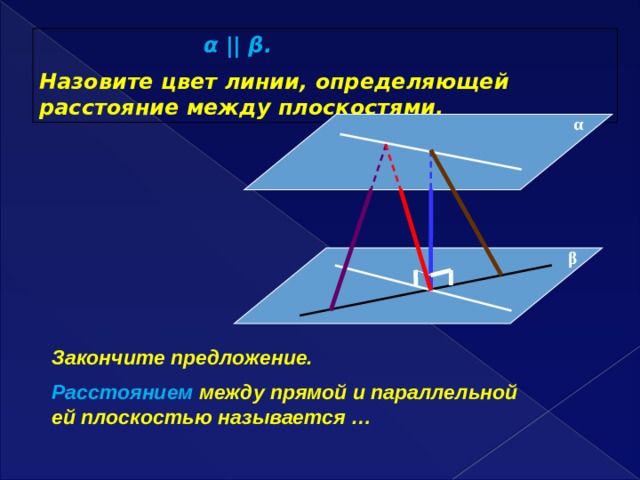
α || β.
Назовите цвет линии, определяющей расстояние между плоскостями.
α
β
Закончите предложение.
Расстоянием между прямой и параллельной ей плоскостью называется …
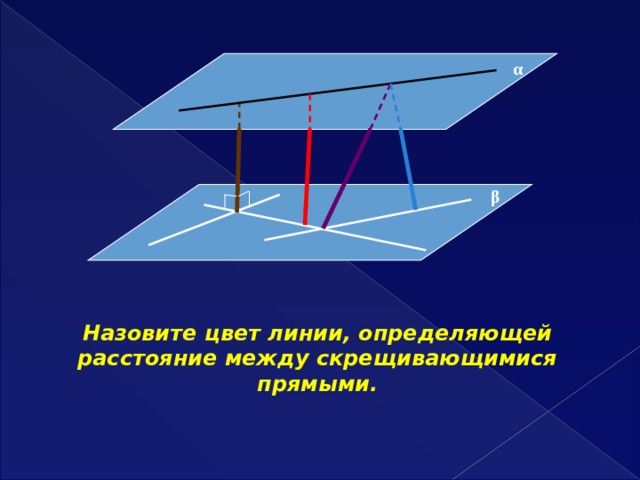
α
β
Назовите цвет линии, определяющей расстояние между скрещивающимися прямыми.
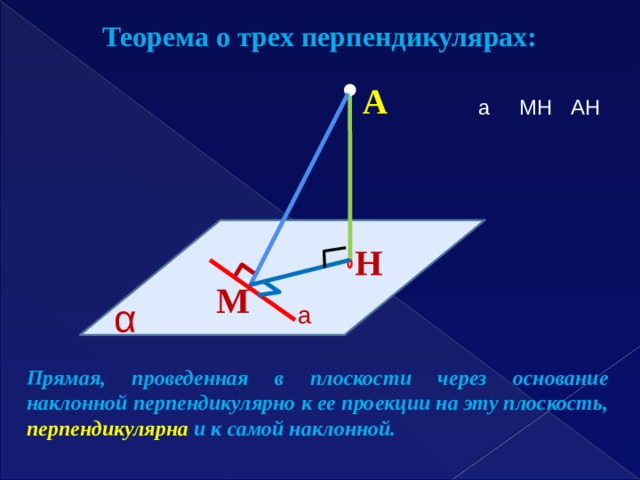
Теорема о трех перпендикулярах:
A
а МH АH
H
М
α
а
Прямая, проведенная в плоскости через основание наклонной перпендикулярно к ее проекции на эту плоскость, перпендикулярна и к самой наклонной.
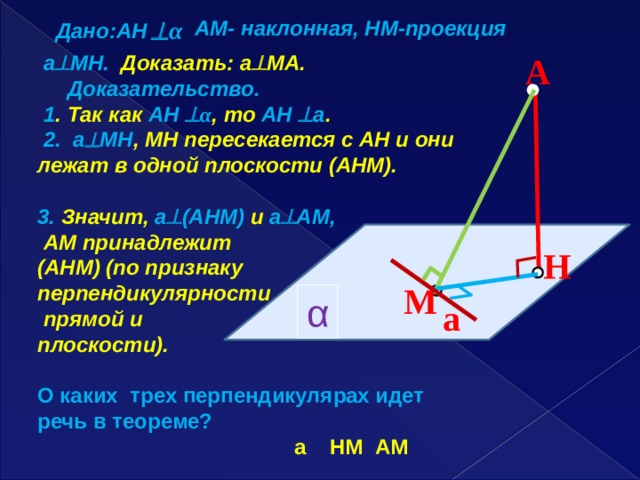
α
AM- наклонная, HM-проекция
Дано:AH
A
а МH. Доказать: а МА.
Доказательство.
1 . Так как АН α , то АН а .
2. а МН , МН пересекается с АН и они лежат в одной плоскости (АНМ).
3. Значит, а (АНМ) и а АМ,
АМ принадлежит
(АНМ) (по признаку
перпендикулярности
прямой и
плоскости).
О каких трех перпендикулярах идет речь в теореме?
а НМ АМ
H
М
α
а
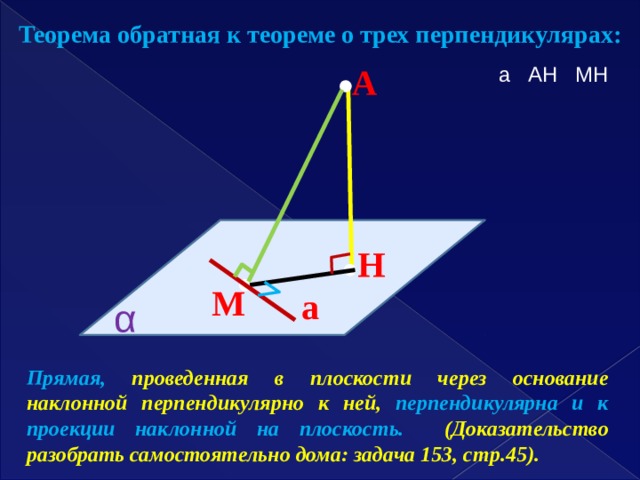
Теорема обратная к теореме о трех перпендикулярах:
A
а AH МH
H
М
а
α
Прямая, проведенная в плоскости через основание наклонной перпендикулярно к ней, перпендикулярна и к проекции наклонной на плоскость. (Доказательство разобрать самостоятельно дома: задача 153, стр.45).
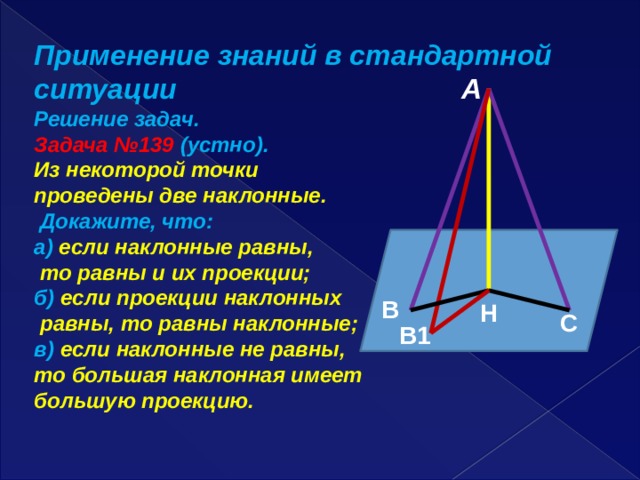
Применение знаний в стандартной ситуации A
Решение задач.
Задача №139 (устно).
Из некоторой точки
проведены две наклонные.
Докажите, что:
а) если наклонные равны,
то равны и их проекции;
б) если проекции наклонных Bb
равны, то равны наклонные;
в) если наклонные не равны,
то большая наклонная имеет
большую проекцию.
B
H
C
B1
AC. Доказать: а)ВН=НС; б) АВ=АС; в)В1НCH. Доказательство: Рассмотрим треугольники АВН и АСН, АН-… а) АВ=АС… треугольники…, Значит, ВН= … ; б) эти треугольники равны, но уже по двум… АВ=АС ; в) АВ1AC . По теореме Пифагора В1Н= HC=; В1НCH . А B H C B1 " width="640"
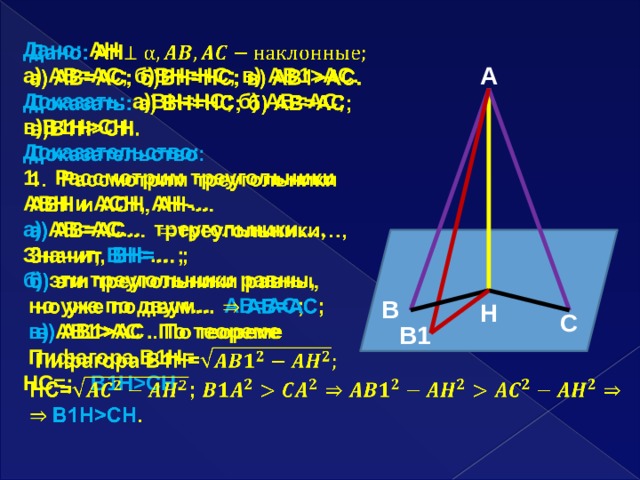
Дано: AH
а) АВ=АС; б)ВН=НС; в) АВ1AC.
Доказать: а)ВН=НС; б) АВ=АС;
в)В1НCH.
Доказательство:
- Рассмотрим треугольники
АВН и АСН, АН-…
а) АВ=АС… треугольники…,
Значит, ВН= … ;
б) эти треугольники равны,
но уже по двум… АВ=АС ;
в) АВ1AC . По теореме
Пифагора В1Н=
HC=; В1НCH .
А
B
H
C
B1
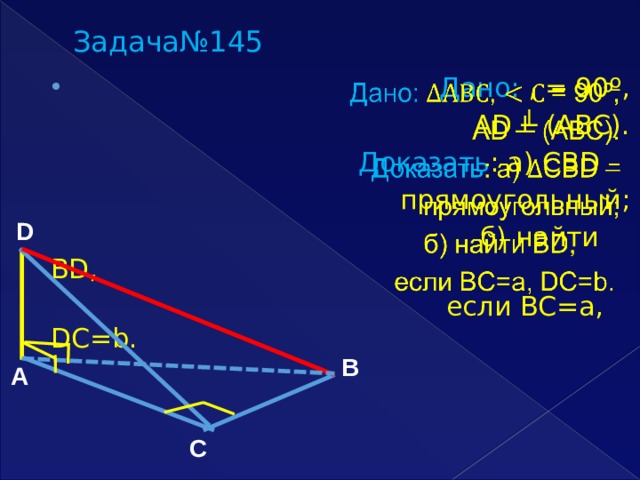
Задача№145
Дано: , = 90º,
AD ┴ (АВС).
Доказать : а) CBD –
прямоугольный;
б) найти BD,
если BC=a, DC=b.
D
B
A
C
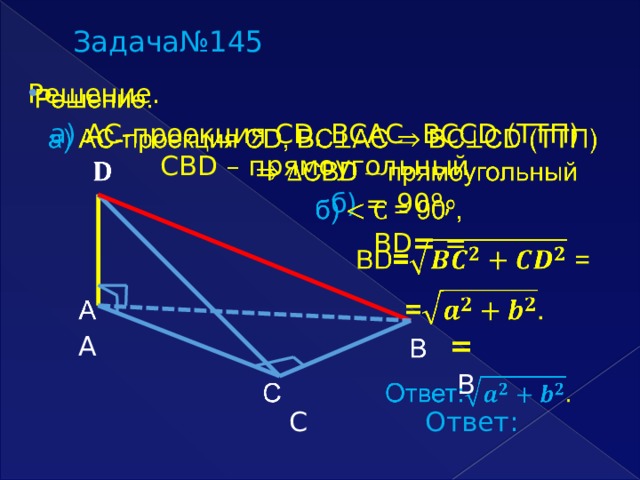
Задача№145
Решение.
а) АС-проекция CD, BCAC BCCD (ТТП) CBD – прямоугольный
б) = 90º,
BD = =
А =
В
С Ответ:
Презентация "Теорема о трех перпендикулярах" (518.13 KB)
0
537
97
Нравится
0
