
Температурная графическая модель значения выражения
Температурная графическая модель значения выражения
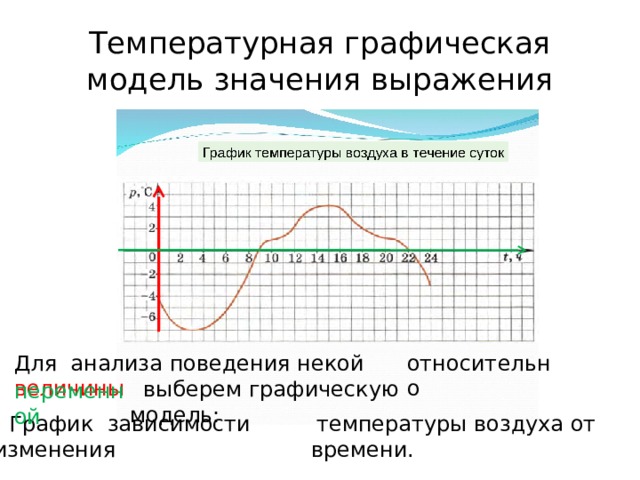
Для анализа поведения некой величины
относительно
выберем графическую модель:
переменной
График зависимости изменения
температуры воздуха от времени.
Температурная графическая модель значения выражения
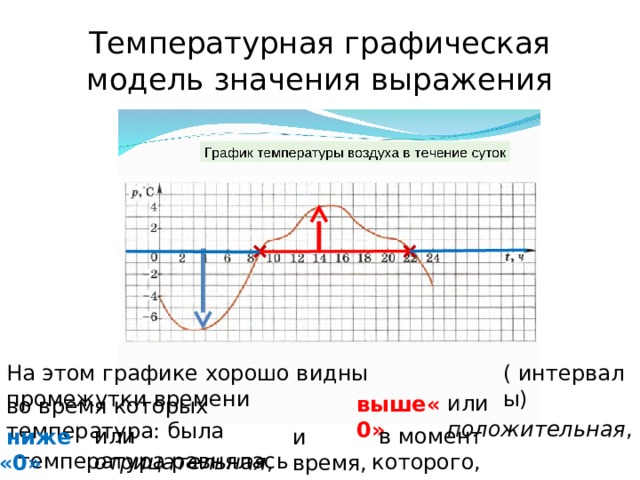
На этом графике хорошо видны промежутки времени
( интервалы)
или положительная ,
выше«0»
во время которых температура: была
или отрицательная ,
в момент которого,
ниже «0»
и время,
температура равнялась нулю.

Температурная графическая модель значения выражения
на координатной плоскости,
Аналогичным образом ,
мы можем построить линию поведения
любой другой зависимой величины.
Такую величину принято обозначать
Y
буквой латинского алфавита :
с указанием в скобках величин
Y ( x )=
от которых она зависит:
(или) фразы
С записью математического выражения
Х
содержащей
Например Y ( х ) = 5 X -15
Температурная графическая модель значения выражения (схематическое построение)
Для примера воспользуемся выражением с предыдущего слайда
Для схематичного определения положительных и отрицательных интервалов выполняем ряд простых действий .
Во многих алгебраических задачах нам не требуется точного построения линии поведения величины на координатной плоскости.
А нужно лишь представление о том, на каких интервалах величина положительна,
Назовём это схематичным определением положительных и отрицательных интервалов.
а на каких отрицательна
Y ( х ) = 5 X -15
В результате получаем.
Что на интервале от -∞ до 3 выражение принимает отрицательные значения
5 X -15=0
- Находим ТПЗ – точки перемены знака выражения.
Они совпадают с корнями уравнения в котором выражение приравнивается к нулю.
2. Чертим числовую прямую и наносим на неё ТПЗ=3. она делит прямую на два луча (интервала)
Берём произвольные значения на каждом интервале
X = 15/ 5
( например левее ТПЗ Х=1,
а правее Х=5)
X =
X =3
а на интервале от 3 до +∞ - положительные
Y ( х ) = 5 ▪1 -15 = -10
X =
-∞
+∞
1
1
3
5
Y ( х ) = 5 ▪5 -15 = +10
5
и подставляя их в выражение Y ( х ) = 5 X -15 . определяем знак получившихся значений
 0 (+) У(-1)= 3(-1)²+12(-1)= -9У(-5)= 3(-5)²+12(-5)= 150(+) " width="640"
0 (+) У(-1)= 3(-1)²+12(-1)= -9У(-5)= 3(-5)²+12(-5)= 150(+) " width="640"
Рассмотрим схематическое построение графической
модели несимметричного выражения
У(х)= 3х²+12х
1. Приравниваем выражение 0 и находим ТПЗ
(корни данного выражения)
по формуле ДКН: Х₁=0 и Х₂=-в/а
3х²+12х=0
Х₁=0
Х₂= -12/3= -4
Рисуем числовую прямую и наносим на неё ТПЗ Х₁=0 и Х₂= -4
I
III
II
-∞
+∞
-5
-4
1
0
-1
2.Получаем 3 интервала нумеруем их справа на лево.
Почему именно так, мы рассмотрим позднее.
II- от -4 до 0
III- от -∞до-4
I - от 0 до +∞
3.Назначаем на них произвольные значения переменной
на II- Х=-1
на I Х=1
на III- Х= -5
4. подставляя эти значения в выражения находим знаки интервалов
У(1)= 3(1)²+12(1)= 150 (+)
У(-1)= 3(-1)²+12(-1)= -9
У(-5)= 3(-5)²+12(-5)= 150(+)
 0 (+) У(-1)= 3(-1)²+12(-1)= -9У(-5)= 3(-5)²+12(-5)= 150(+) " width="640"
0 (+) У(-1)= 3(-1)²+12(-1)= -9У(-5)= 3(-5)²+12(-5)= 150(+) " width="640"
Рассмотрим схематическое построение графической
модели несимметричного выражения без теории
У(х)= 3х²+12х
ДКН: Х₁=0 и Х₂=-в/а
3х²+12=0
Х₂= -12/3= -4
Х₁=0
I
II
III
-∞
+∞
-5
1
-4
0
-1
У(1)= 3(1)²+12(1)= 150 (+)
У(-1)= 3(-1)²+12(-1)= -9
У(-5)= 3(-5)²+12(-5)= 150(+)

 Получите свидетельство
Получите свидетельство Вход
Вход












 Презентация "Температурная графическая модель значения выражения" (642.57 KB)
Презентация "Температурная графическая модель значения выражения" (642.57 KB)
 0
0 136
136 2
2 Нравится
0
Нравится
0


