Презентация "Решение экономических задач в Excel "

Решение экономических задач в Excel

Полезные хитрости, которые облегчат работу с Excel

Функции в Excel

Функции  — программы , которые можно вызывать по имени для выполнения определенных действий.

( Функции представляют собой заранее определенные формулы, которые выполняют вычисления по заданным величинам, называемым аргументами, и в указанном порядке)

Пример:

Функция

=ОСТАТ(5; 2)

Описание

Результат

Остаток от деления 5 на 2

1

Формулы могут включать функции. Функции могут вводиться в таблицу в составе формул либо отдельно. Функцию так же, как и число, можно считать частным случаем формулы.

Синтаксис функции

= ИМЯ_ФУНКЦИИ ( аргумент1;аргумент2 ;…)

Например:

= КОРЕНЬ (9) – расчет корня квадратного числа 9

= СЕГОДНЯ () – определение текущей даты, данные не нужны

= SIN (С8) – расчет синуса угла, заданного в ячейке С8

Скобки — обязательная принадлежность функции, даже если у нее нет аргументов, например функция =ПИ() — 3,1416... (Если аргументов нет, то скобки остаются пустыми.)

Если аргументов несколько, то один аргумент от другого отделяется точкой с запятой .

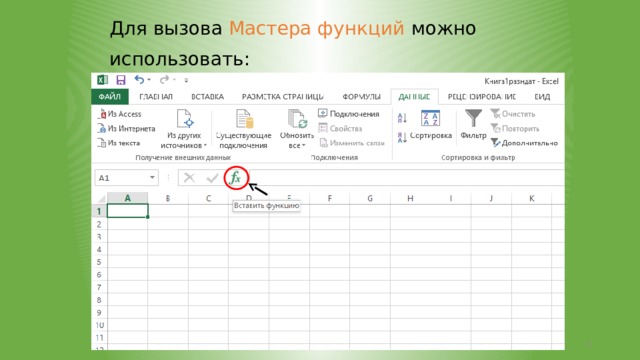
Для вызова Мастера функций можно использовать:

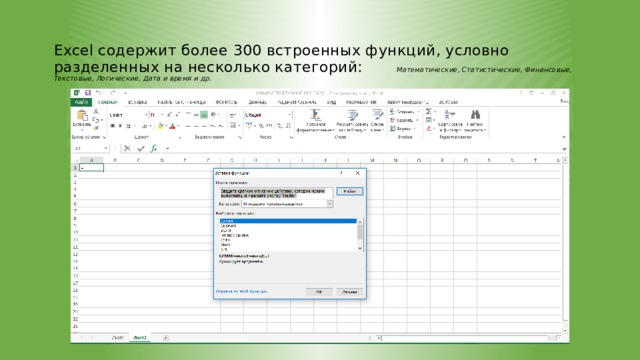
Excel содержит более 300 встроенных функций, условно разделенных на несколько категорий: Математические, Статистические, Финансовые, Текстовые, Логические, Дата и время и др.

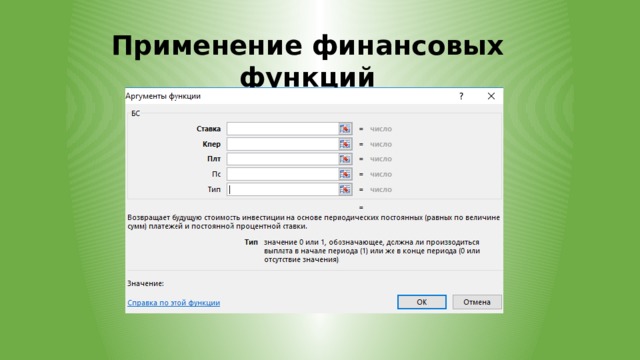
Применение финансовых функций

Аргументы финансовых функций:

БС – будущая (конечная) сумма

Ставка – процентная ставка за 1 период выплат

КПЕР – кол-во периодов выплаты (вклада, кредита)

ПЛТ – размер выплат за 1 период

ПС – начальное значение суммы

Тип – выплата в конце (0) или начале периода (1)

Очень важно! Запомните правило:

Если мы платим деньги, даже если помещаем их на свой счет в банке, и в нашем кошельке деньги уменьшаются , то соответствующий аргумент будет иметь знак « - ».

Если деньги платят нам , даже если мы получаем их со своего счета в банке, и в нашем кошельке деньги увеличиваются , то аргумент будет иметь знак « + ».

КПЕР – сколько раз будут производиться платежи.

Например, если вы выплачиваете кредит 2 года каждый месяц, то КПЕР=2×12=24.

Если вы выплачиваете этот же кредит один раз в год, то КПЕР=2.

СТАВКА – процентная ставка за период.

Например, если вы берете кредит под 12% годовых и выплачиваете его каждый месяц, то СТАВКА=12%÷12мес.=1%.

А если за этот же кредит вы будете расплачиваться только один раз в год, то

СТАВКА=12%.

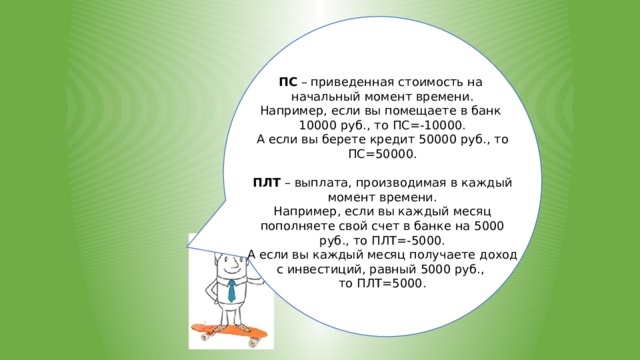
ПС – приведенная стоимость на

начальный момент времени.

Например, если вы помещаете в банк

10000 руб., то ПС=-10000.

А если вы берете кредит 50000 руб., то ПС=50000.

ПЛТ – выплата, производимая в каждый момент времени.

Например, если вы каждый месяц пополняете свой счет в банке на 5000 руб., то ПЛТ=-5000.

А если вы каждый месяц получаете доход с инвестиций, равный 5000 руб.,

то ПЛТ=5000.

Функция БС (ставка;кпер;плт ;[пс];[тип] )

возвращает будущую стоимость инвестиций на основе периодических постоянных платежей и процентной ставки.

Пример 1. Мы помещаем 20000 руб. в банк с начислением 7% годовых. Начисления проводятся каждый месяц.

Вопрос:

Сколько денег окажется на нашем счету через 5 лет?

Мы помещаем 20000 руб. в банк с начислением 7% годовых. Начисления проводятся каждый месяц.

Решение задачи

• Определяем ставку за 1 период, который у нас равен

1 месяцу:

7% в год / 12 мес.

• Определяем количество периодов начисления процентов:

5 лет  12 мес=60.

• Аргумент ПЛТ=0, т.к. в течение 5 лет мы вклад не пополняем и деньги не забираем.
• Аргумент ПС будет иметь знак «-», т.к. первоначально мы вкладываем деньги, а не получаем их.

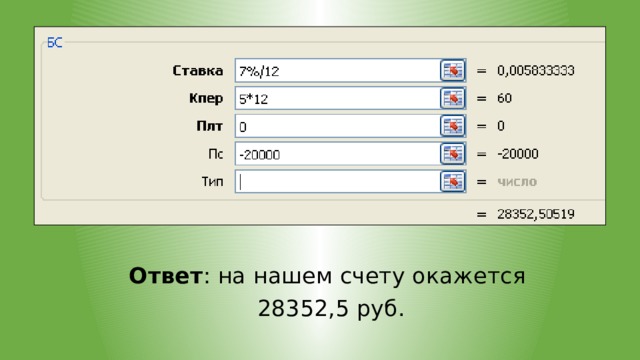
Ответ : на нашем счету окажется

28352,5 руб.

Функция ПС ( ставка; кпер; плт; [бс]; [тип] )

возвращает приведенную к начальному времени стоимость инвестиций.

Пример 2. Мы хотим накопить 100000 руб. через 5 лет, вложив в банк под 9% годовых определенную сумму. Проценты будут начисляться каждый месяц.

Вопрос:

Какую сумму мы должны положить в банк?

Мы хотим накопить 100000 руб. через 5 лет, вложив в банк под 9% годовых определенную сумму. Проценты будут начисляться каждый месяц.

Решение

• Определяем ставку за 1 период, который у нас равен 1 месяцу:

9% в год / 12 месяцев.

• Определяем количество периодов начисления процентов:

5 лет  12 мес.=60.

• Аргумент ПЛТ=0, т.к. размер периодических платежей=0.
• Аргумент БС=100000 – это та сумма, которую мы хотим получить через 5 лет.

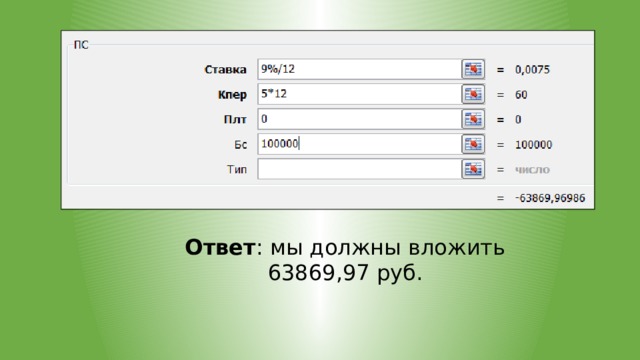
Ответ : мы должны вложить 63869,97 руб.

Функция ПЛТ (ставка; кпер; плт; [бс]; [тип])

возвращает сумму постоянных периодических платежей при условии неизменной процентной ставки.

Пример 3. Мы берем ипотеку 1000000 руб. Годовая ставка - 12%. Хотим полностью рассчитаться с банком за 15 лет, выплачивая долг каждый месяц.

Вопрос:

Чему будут равны наши платежи?

Мы берем ипотеку 1000000 руб. Годовая ставка - 12%. Хотим полностью рассчитаться с банком за 15 лет, выплачивая долг каждый месяц.

Решение

• Определяем ставку за 1 период, который у нас равен

1 месяцу:

12% в год / 12 месяцев.

• Определяем количество выплат:

15 лет  12 мес.=180.

• Аргумент ПС=1000000 – сумма, которую мы берем в долг.
• Аргумент БС=0 – через 15 лет наш долг должен быть равен 0 рублей.

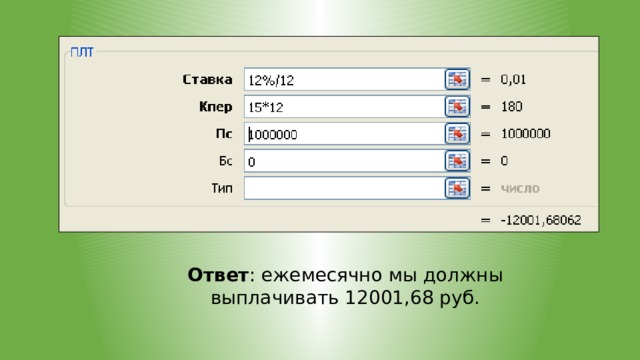
Ответ : ежемесячно мы должны выплачивать 12001,68 руб.

Функция КПЕР (ставка;плт;пс;[бс];[тип])

возвращает количество периодов выплат при постоянных платежах и неизменной процентной ставке.

Пример 4. Человек, начиная с 18-летнего возраста, начинает каждый месяц вкладывать в банк 3000 руб. Годовая ставка банка 8%.

Вопрос:

В каком возрасте человек станет миллионером?

Человек, начиная с 18-летнего возраста, начинает каждый месяц вкладывать в банк 3000 руб.

Годовая ставка банка 8%.

Решение

• Определяем величину процентной ставки за период: 8%/12 мес.=0,66%.

• Аргумент ПЛТ=-3000 – сумма, которую человек ежемесячно добавляет на свой счет.
• Аргумент БС=1000000 – человек хочет стать миллионером!
• Аргумент ПС=0 – накапливать деньги человек будет начинать с нуля.

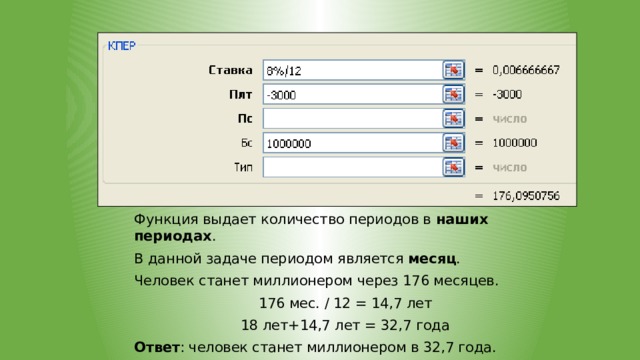
Функция выдает количество периодов в наших периодах .

В данной задаче периодом является месяц .

Человек станет миллионером через 176 месяцев.

176 мес. / 12 = 14,7 лет

18 лет+14,7 лет = 32,7 года

Ответ : человек станет миллионером в 32,7 года.