Презентация " Практические приложения подобия треугольников"

Теория без практики мертва или бесплодна, практика без теории невозможна или пагубна. Для теории нужны знания, для практики, сверх того, и умения.

Тема. Практические приложения подобия треугольников.

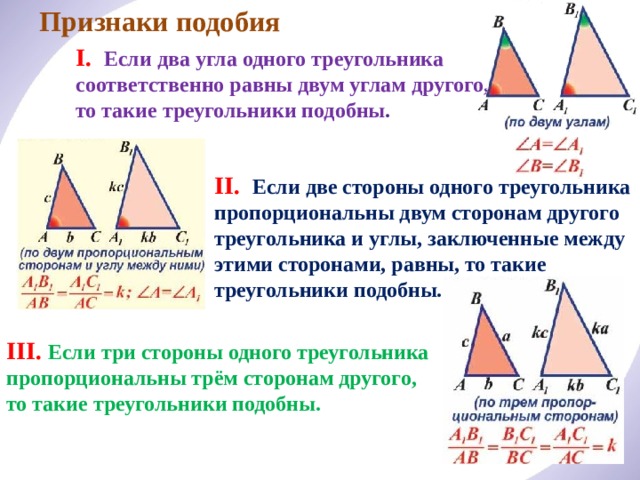
Признаки подобия

I. Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны .

II. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны.

III. Если три стороны одного треугольника пропорциональны трём сторонам другого, то такие треугольники подобны.

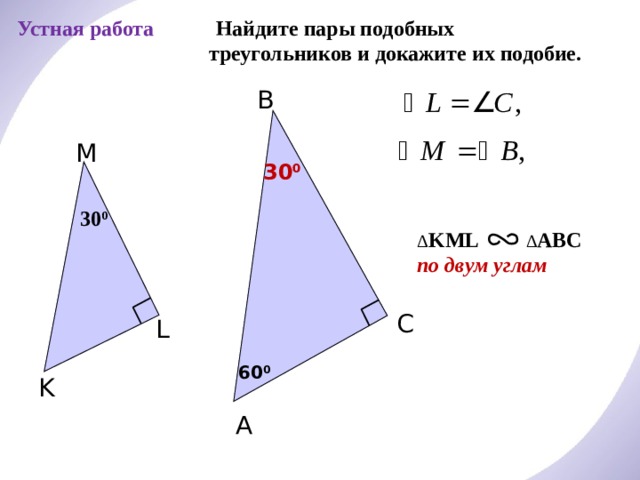
Устная работа

Найдите пары подобных треугольников и докажите их подобие.

B

M

30 0

30 0

Δ KML ∆ ABC

по двум углам

C

С.М. Саврасова, Г.А. Ястребинецкий «Упражнения по планиметрии на готовых чертежах»

L

60 0

K

A

4

40 0

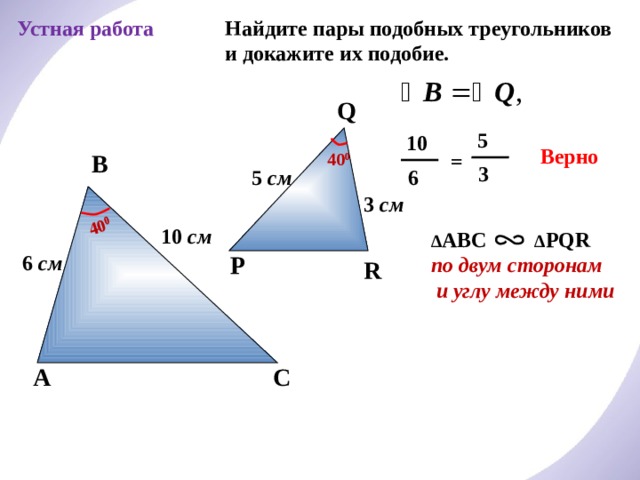
Найдите пары подобных треугольников и докажите их подобие.

Устная работа

Q

5

10

Верно

40 0

=

В

3

5 см

6

3 см

10 см

∆ ABC ∆ PQR

по двум сторонам

и углу между ними

Р

6 см

R

С.М. Саврасова, Г.А. Ястребинецкий «Упражнения по планиметрии на готовых чертежах»

С

А

5

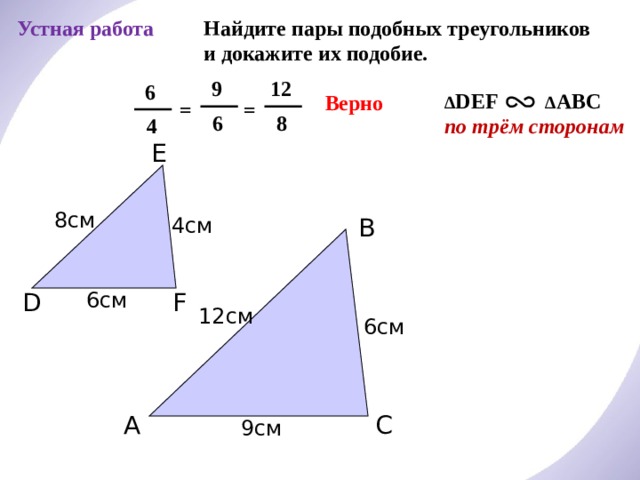
Устная работа

Найдите пары подобных треугольников и докажите их подобие.

12

9

6

∆ DEF ∆ ABC

по трём сторонам

Верно

=

=

8

6

4

E

8см

4см

B

6см

F

D

12см

С.М. Саврасова, Г.А. Ястребинецкий «Упражнения по планиметрии на готовых чертежах»

6см

C

A

9см

6

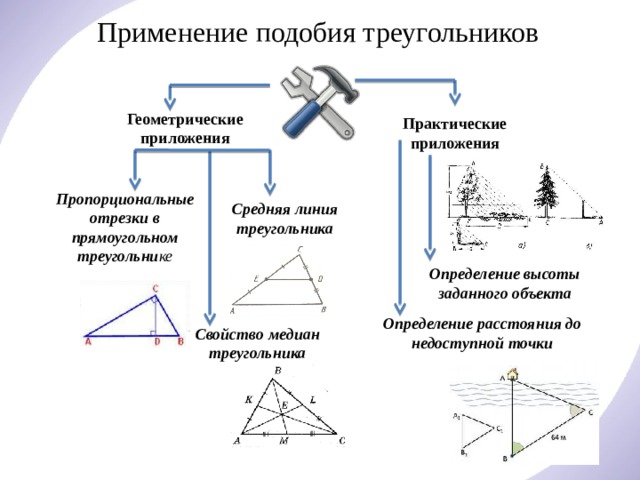
Применение подобия треугольников

Геометрические приложения

Практические приложения

Пропорциональные отрезки в прямоугольном треугольни ке

Средняя линия треугольника

Определение высоты заданного объекта

Определение расстояния до недоступной точки

Свойство медиан треугольника

Если высказывание истинно – отвечаем “Да”, если ложно – “Нет”

• Два треугольника подобны, если их углы соответственно равны и сходственные стороны пропорциональны.
• Два равносторонних треугольника всегда подобны.
• Если три стороны одного треугольника соответственно пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.
• Стороны одного треугольника имеют длины 3, 4, 6 см, стороны другого треугольника равны 9, 14, 18 см. Подобны ли эти треугольники?
• Периметры подобных треугольников относятся как квадраты сходственных сторон.
• Если два угла одного треугольника равны 60° и 50° , а два угла другого треугольника равны 50° и 80°, то такие треугольники подобны.
• Два прямоугольных треугольника подобны, если имеют по равному острому углу.
• Два равнобедренных треугольника подобны, если их боковые стороны пропорциональны.
• Если отрезки гипотенузы, на которые она делится высотой, проведенной из вершины прямого угла, равны 2 и 8 см, то эта высота равна 4 см.
• Если медиана треугольника равна 9 см, то расстояние от вершины треугольника до точки пересечения медиан равно 6 см.

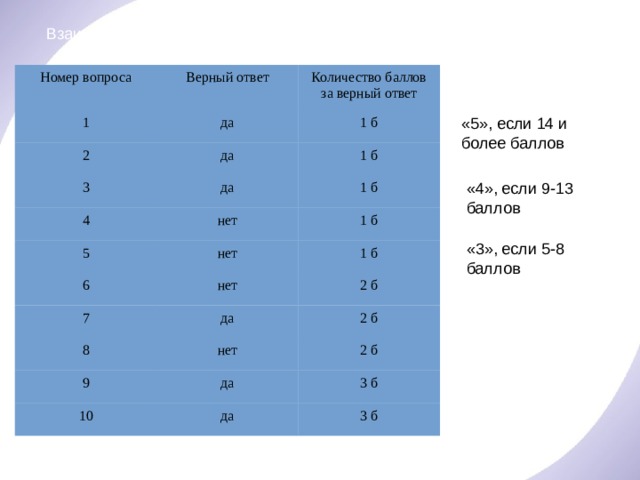
Взаимопроверка

Номер вопроса

Верный ответ

1

да

2

Количество баллов за верный ответ

1 б

да

3

1 б

4

да

1 б

нет

5

1 б

нет

6

нет

1 б

7

2 б

8

да

2 б

нет

9

2 б

да

10

3 б

да

3 б

«5», если 14 и более баллов

«4», если 9-13 баллов

«3», если 5-8 баллов

Всё ли в природе можно измерить?

Возможно ли измерить недоступное?

Немного истории

Египтяне задали греческому мудрецу Фалесу задачу: найти высоту одной из пирамид. Фалес нашел простое и красивое решение. Он воткнул в землю вертикально палку и сказал: « Когда тень от этой палки будет той же длины, что и сама палка, тень от пирамиды будет иметь ту же длину, что и высота пирамиды ».

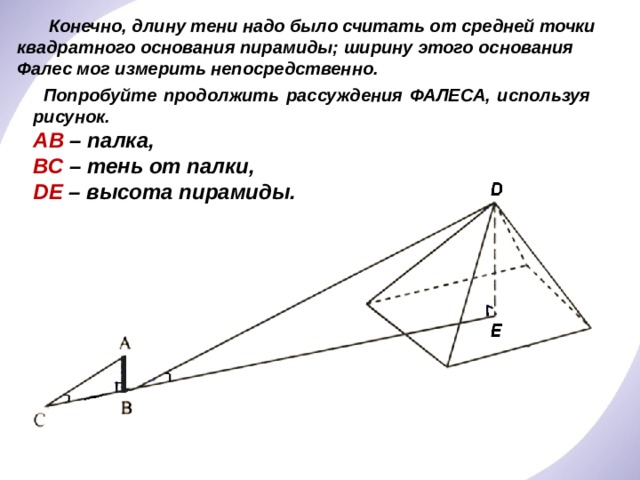
Конечно, длину тени надо было считать от средней точки квадратного основания пирамиды; ширину этого основания Фалес мог измерить непосредственно.

Попробуйте продолжить рассуждения ФАЛЕСА, используя рисунок.

АВ – палка,

ВС – тень от палки,

DЕ – высота пирамиды.

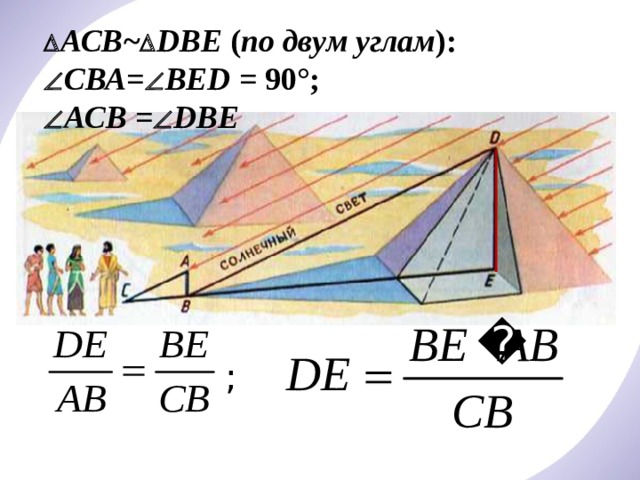
 АСВ ~  DВE ( по двум углам ):

 СВА =  ВED = 90°;

 АСВ =  DВЕ

;

И змерение высоты скалы героями книги Жюля Верна «Таинственный остров»

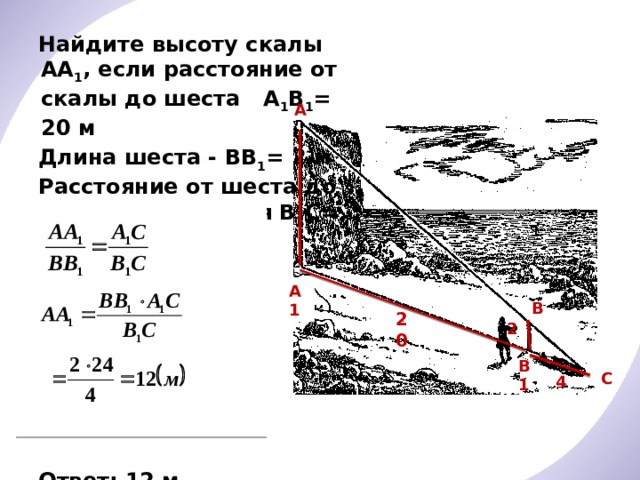
Найдите высоту скалы АА 1 , если расстояние от скалы до шеста А 1 В 1 = 20 м

Длина шеста - ВВ 1 = 2 м

Расстояние от шеста до

точки наблюдения В 1 С= 4 м

Решение:

Ответ: 12 м

А

А1

В

20

2

В1

С

4

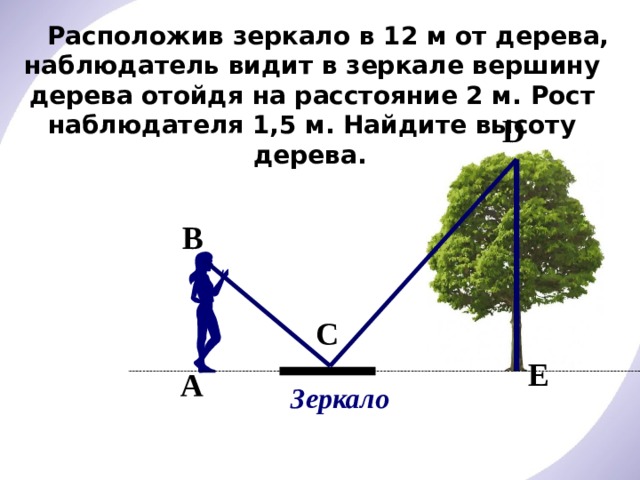
Расположив зеркало в 12 м от дерева, наблюдатель видит в зеркале вершину дерева отойдя на расстояние 2 м. Рост наблюдателя 1,5 м. Найдите высоту дерева.

D

В

C

E

А

Зеркало

D

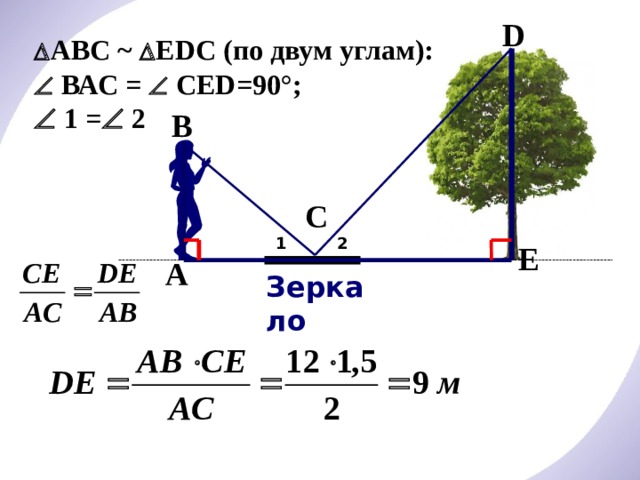
 АВС ~  ЕDС (по двум углам):

 ВАС =  СED=90°;

 1 =  2

В

С

2

1

E

А

Зеркало

Тень дерева равна 10 метров, рост мальчика равен 1,5 метра, а его тень 3 метра. Найдите высоту дерева.

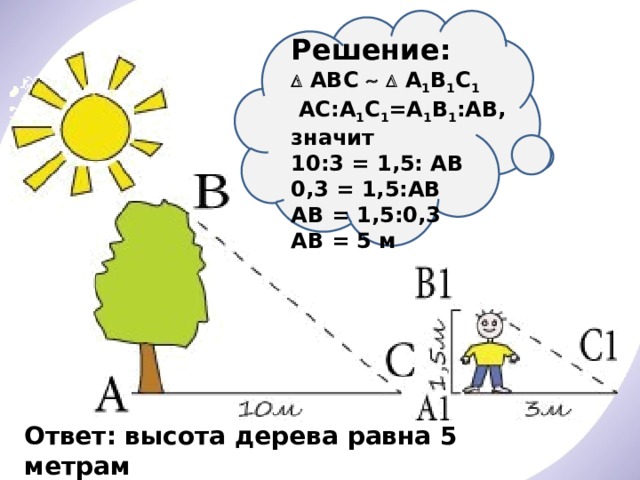
Решение:

 АВС   А 1 В 1 С 1

AC:A 1 C 1 =A 1 B 1 :AB, значит

10:3 = 1,5: AB

0,3 = 1,5:AB

AB = 1,5:0,3

AB = 5 м

Ответ: высота дерева равна 5 метрам

Длина тени человека ростом 1,7 равна 2,55 м. Длина тени Эйфелевой башни 486м. Найти высоту Эйфелевой башни.

Решение: ∆ АBC ∼ ∆ A 1 B 1 C 1 ;т.к ∠BCA=∠B 1 C 1 A= 90° ∠BAC=∠B 1 A 1 C 1 , т.к. свет падает в один и тот же момент под прямым углом. 1,7 = x 2,55 486 x= 1,7·486 2,55 х=324 Ответ: 324 м высота Эйфелевой башни.

Рефлексия

• Что больше всего запомнилось на уроке?

«Я запомнил, что …»

• Что удивило?

«Оказывается, что …»

• Что понравились больше всего?

«Мне понравилось …»