Презентация по теме системы линейных уравнений

Системы двух линейных уравнений с двумя неизвестными

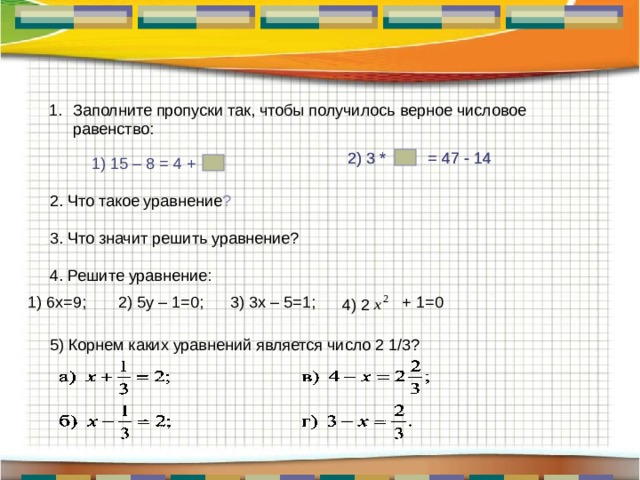
• Заполните пропуски так, чтобы получилось верное числовое равенство:

2) 3 *

= 47 - 14

2) 3 *

= 47 - 14

1) 15 – 8 = 4 +

2. Что такое уравнение ?

3. Что значит решить уравнение?

4. Решите уравнение:

1) 6х=9;

2) 5у – 1=0;

3) 3х – 5=1;

+ 1=0

4) 2

5) Корнем каких уравнений является число 2 1/3?

Задача. Обозначив за х первое число и за у второе число, составьте соотношение по следующим условиям:

а) первое число на 5 больше второго:

х – у = 5

б) сумма квадрата первого числа и удвоенного второго числа равна 17:

в) утроенное произведение чисел равно 24:

3ху = 24.

г) разность куба первого числа и половины второго числа равна 12:

Это примеры уравнений

с двумя неизвестными

Примеры уравнений с двумя неизвестными:

В чем отличия уравнений первого и второго столбиков?

Как в общем виде можно записать примеры второго столбца?

• линейные уравнения

с двумя неизвестными

ах + b у = с

Уравнения с двумя переменными обладают такими же свойствами, как и уравнения с одной переменной, а значит, при их решении можно выполнять аналогичные преобразования.

Благодаря этому появляется возможность выражать в таких уравнениях одну переменную через другую.

Задача . В двух седьмых классах учится 57 школьников. В 7а классе на 5 школьников больше, чем в 7б классе. Сколько учащихся в каждом классе?

Пусть в 7а – х учащихся, в 7б – у учащихся, тогда

х + у = 57,

х – у = 5

По условию задачи составили два линейных уравнения с двумя переменными (или неизвестными).

Необходимо найти такие значения переменных х и у, при которых каждое из уравнений будет верным равенством, т.е.найти общее решение этих уравнений.

Пара чисел х=31 и у=26 удовлетворяет каждому уравнению, так как при их подстановке получаем верные числовые равенства.

х + у = 57

- система двух линейных уравнений с двумя неизвестными

х – у = 5

Что будет решением системы двух уравнений с двумя неизвестными?

Что значит решить системы уравнений?

№ 619 .

Как, не решая систему уравнений, определить, сколько решений она имеет?

- Рассмотрим систему:

- Выразим из каждого уравнения у через х:

! Уравнения задаются линейными функциями.

Угловые коэффициенты прямых, являющихся графиками этих функций, различны.

Значит прямые пересекаются и система имеет единственное решение.

Если

к1 ≠ к2

Графики

пересекаются

Если

к1 = к2,

b 1 ≠ b 2

Система имеет единственное решение

Графики параллельны

Если

к1=к2,

b1=b2

Система не имеет решений

Графики совпадают

Система имеет бесконечно много решений

(по рядам) Выяснить, сколько решений имеет система.

1.

2.

3.

ПРОВЕРКА :

к1 = к2= - 0,5

b 1 ≠ b 2

к1=к2,

b1=b2

к1

к2

Система имеет единственное

решение

Система имеет бесконечно

много решений

Система не имеет решений

Является ли решением системы уравнений

пара (3;1) пара (2;2)

верно

верно

неверно

верно

(3;1) не является решением

(2;2) является решением

Итог урока

Дай определение:

• линейное уравнение с двумя неизвестными;

• системы уравнений;
• решение системы двух линейных уравнений с двумя неизвестными