Презентация по геометрии "Построение сечений тетраэдра и параллелепипеда"

Построение сечений тетраэдра и параллелепипеда

Автор : Крылова Алина Викторовна,

учитель математики

МБОУ «Видновская СОШ №2»

Ленинский г. о. Московской области

2020 г.

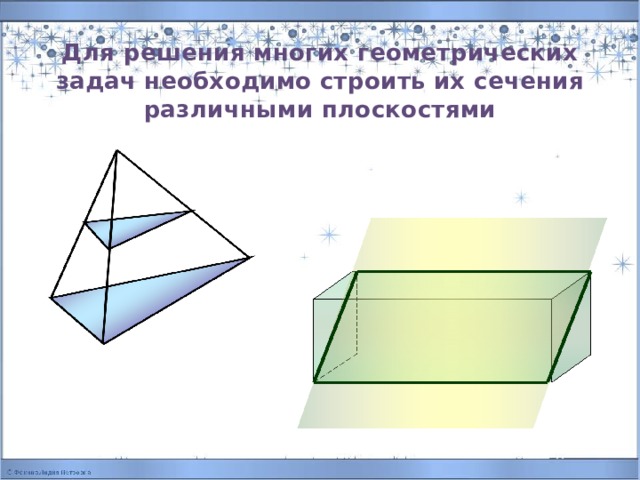
Для решения многих геометрических задач необходимо строить их сечения различными плоскостями

Сечение тетраэдра и параллелепипеда

Секущей плоскостью тетраэдра или параллелепипеда называется любая плоскость, по обе стороны от которой имеются точки данного тетраэдра или параллелепипеда.

Секущая плоскость пересекает грани тетраэдра (параллелепипеда) по отрезкам

• Многоугольник, сторонами которого являются данные отрезки, называется сечением тетраэдра (параллелепипеда).

Построение сечений

• Для построения сечения нужно построить точки пересечения секущей плоскости с ребрами и соединить их отрезками.

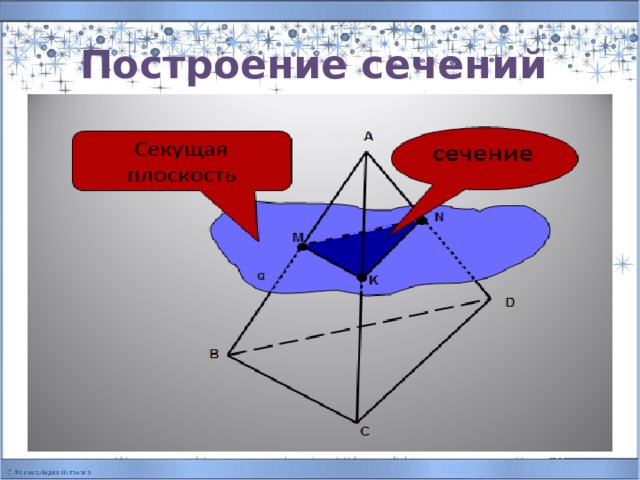
Построение сечений

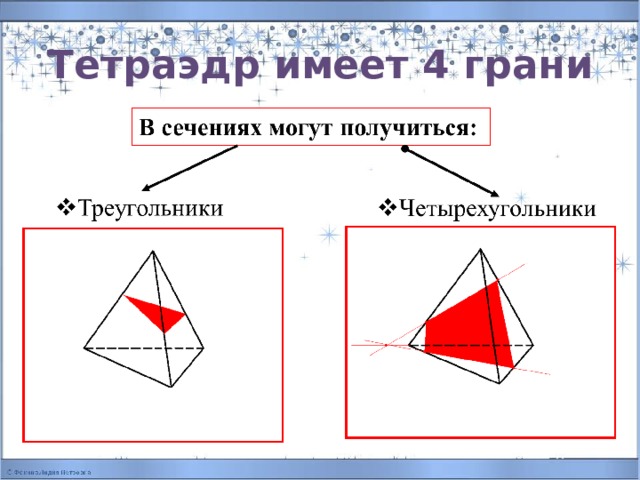
Тетраэдр имеет 4 грани

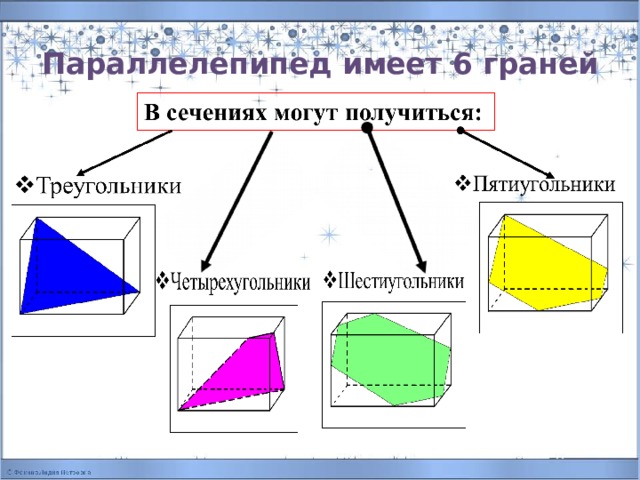
Параллелепипед имеет 6 граней

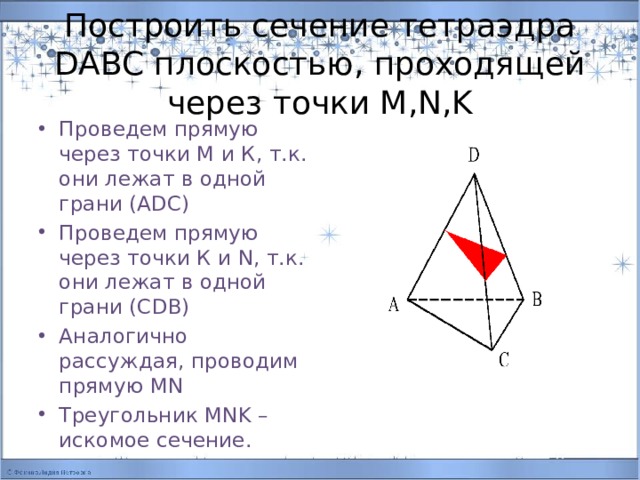
Построить сечение тетраэдра DABC плоскостью, проходящей через точки M,N,K

• Проведем прямую через точки М и К, т.к. они лежат в одной грани (АDC)
• Проведем прямую через точки К и N, т.к. они лежат в одной грани (СDB)
• Аналогично рассуждая, проводим прямую MN
• Треугольник MNK –искомое сечение.

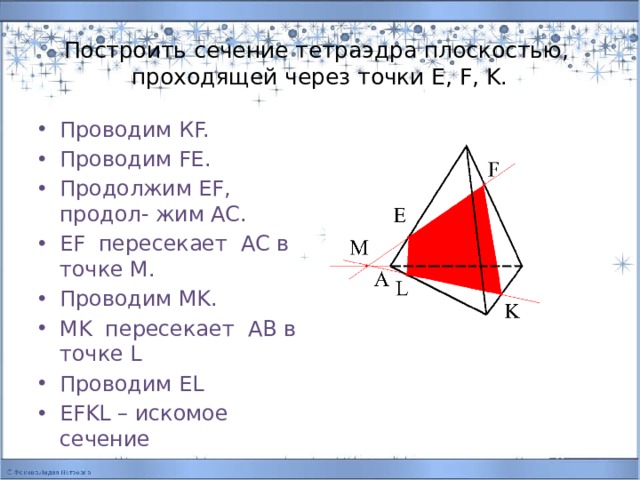
Построить сечение тетраэдра плоскостью, проходящей через точки E, F, K.

• Проводим КF.
• Проводим FE.
• Продолжим EF, продол- жим AC.
• EF пересекает AC в точке М.
• Проводим MK.
• MK пересекает AB в точке L
• Проводим EL
• EFKL – искомое сечение

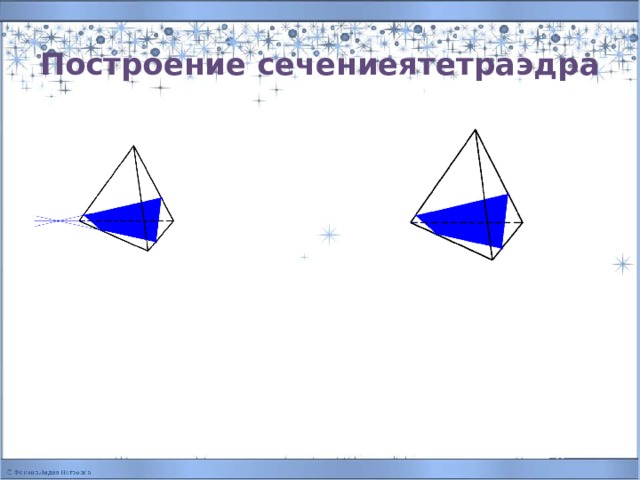
Построение сечениеятетраэдра

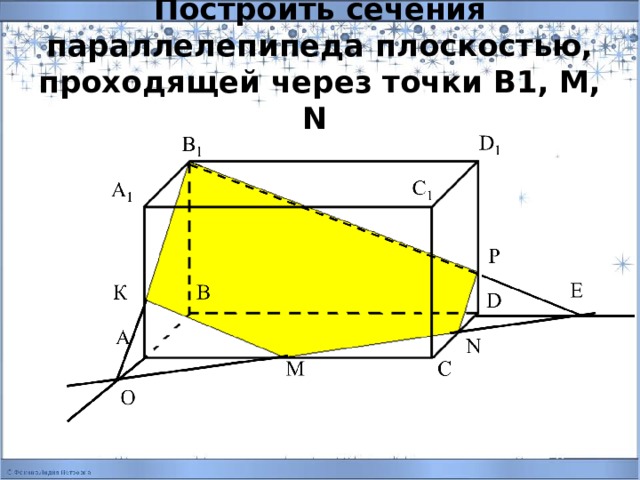
Построить сечения параллелепипеда плоскостью, проходящей через точки В1, М, N

План построения

1. MN

2.Продолжим MN,ВА

3.MN ∩ BA=O

4. В1О

5. В1О ∩ А1А=К

6. КМ

7. Продолжим MN и BD

8. MN ∩ BD=E

9. В1E

10. B1Е ∩ D1D=P , PN

11. KB1PNM – сечение.

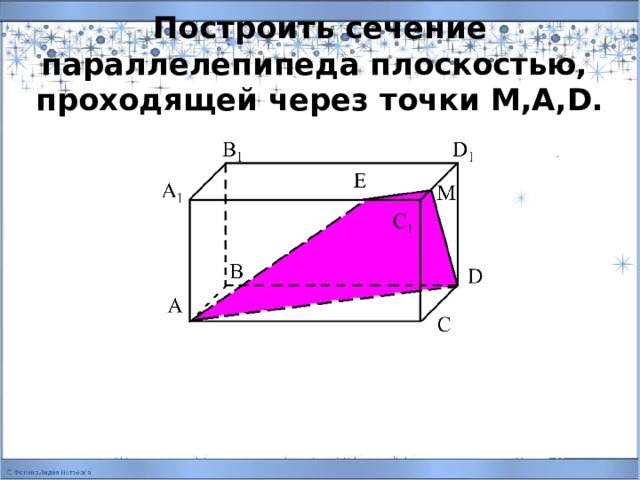
Построить сечение параллелепипеда плоскостью, проходящей через точки M,A,D.

План построения

1. AD

2. MD

3. ME//AD, т.к. (ABC)//(A1B1C1)

4. AE

5. AEMD – сечение.

СПАСИБО ЗА ВНИМАНИЕ!