Презентация НПК "Первые шаги в науку"

Научно практическая конференция школьников. «Первые шаги в науку.»

Направление : математика

Название работы : Решение старинных задач .

Автор работы : Мучкаев Василий Анатольевич

Место выполнения работы : Муниципальное бюджетное

образовательное учреждение « Среднее общеобразовательная

школа № 8 имени Номто Очирова», г. Элиста.

  Руководитель: Шаваева В. Э.

2017г.

Оглавление

Введение…………………………………………………………..3 стр.

Глава 1. Изучить различные старинные задачи…………….4стр.

. 1. Кому пасти овец?................................................... 5 стр.

2.На мельнице………………………………………….4 стр.

3. Воз сена…………………………………………….7 стр.

4. .На охоте …………………………………………….8 стр.

5. Мальчики и яблоки……………………………...9 стр.

6. № 190 …………………………………………..10 стр.

Глава 2. Сравнить методы решения задач из старых

учебников математики с современными

способами решения….………..…………………11 стр.

Глава 3. Вывод …………………………………………..…12 стр.

Заключение………………………………………………....13 стр.

Список литературы…………………………………………14 стр.

Цель:

Изучить различные виды старинных задач разных стран.

Сравнить методы решения задач из старых учебников математики с современными способами решения.

Сделать вывод.

Задачи:

- Познакомиться с решениями старинных задач, предложенных авторами первых учебников математики;

-разобрать решение старинных задач с применением современных для нас способов: составляя уравнения, системы уравнений.

-продолжить работу по развитию логического мышления, умению анализировать условия задания, сопоставлять данные факты, делать выводы и отстаивать свою точку зрения.

Гипотеза: В озможно ли решать старинные задачи современными способами ? Предмет исследования: Решение старинных задач . Методы исследования: Анализ литературы, интернет- источников. Разбор решения задач, предлагаемые авторами источников. Поиски решения этих же задач с помощью современных методов. Анализ результатов.

Математика - самая древняя из наук, она была и остается необходимой людям. Слово «математика» греческого происхождения. Оно означает «наука», «размышления». В древности часто полученные знания, открытия старались сохранить в тайне. Например, в школе Пифагора запрещено было делиться своими записями с непифогорцами. За нарушение этого правила один из учеников, требовавший свободного обмена знаниями, - Гиппас был изгнан из школы. Сторонников Гиппаса стали называть математиками, т.е. приверженцами науки. Все без исключения начинают изучать основы математики уже с первых классов школы, потому что эта наука нужна всем, особенно сейчас, когда математика проникла во все отрасли знаний – физику и химию, науки о языке и медицину, астрономию и биологию и т.д. Математики учат вычислительные машины сочинять стихи и музыку, измерять размеры атомов и проектировать плотины электростанций. Математика необходима в любой профессии, какую бы не выбрали для себя. Но кроме того, вы могли заметить: это и очень интересная и удивительная наука. Любите ее. Если даже вы и не станете математиками, знания пригодятся вам в любой отрасли производства.  

Задача 1 . « Кому пасти овец?»

У пятерых крестьян – Ивана, Петра, Якова, Михаила и Герасима – было 10 овец. Не могли они найти пастуха, чтобы пасти овец, и говорит Иван остальным: « Будем братцы, пасти овец по очереди- по столько, сколько каждый из нас имеет овец». По сколько дней должен каждый крестьянин пасти овец, если известно, что у Ивана в два раза меньше овец, чем у Петра, у Якова в два раза меньше, чем у Ивана; Михаил имеет овец в два раза больше, чем Яков, а Герасим – вчетверо меньше, чем Петр?

: Решение, предложенное автором :

а) Из условия следует, что и у Ивана и у Михаила вдвое больше овец, чем у Якова, у Петра вдвое больше, чем у Ивана, и, значит, вчетверо больше, чем у Якова. Но тогда у Герасима столько же овец, сколько имеет их Яков. Общее число овец поэтому в (2+4+1+2+1) = 10 раз больше, чем число овец у Якова. Отсюда следует, что у Якова 1 овца, тогда и у Ивана и у Михаила по 2 овцы, у Петра 4 и у Герасима 1 овца. Соответственно столько же дней должен пасти овец каждый из них.

б)Эту задачу можно решить иначе.

Поскольку Герасим имеет вчетверо меньше овец,чем Петр, то у Петра либо 4 овцы, либо 8 овец.

Если у Петра 8 овец, то у Герасима 2 овцы.

Поскольку 8+2 = 10 и так как еще овец имеют

Иван, Яков и Михаил, то общее число овец уже будет больше 10. Следовательно, у Петра 4 овцы,

а тогда у Герасима одна овца, у Ивана в два раза

меньше, чем у Петра, т. е. 2 овцы, у Якова в два

раза меньше, чем у Ивана, т. е. одна овца, а

у Михаила две овцы, поскольку у него в

два раза больше, чем у Якова.

Решение с помощью уравнения: Пусть - х овец было у Ивана .

Зная, что у пятерых крестьян 10 овец, составим и решим уравнение:

=10

5х = 10

х = 2

У Ивана -2 овцы.

У Петра - 4 овцы.

У Якова -1 овца.

У Михаила - 2 овцы.

У Герасима -1 овца.

Ответ : У Ивана -2 овцы, у Петра – 4 овцы, у Якова --1 овца, у Михаила – 2 овцы , у Герасима -1 овца.

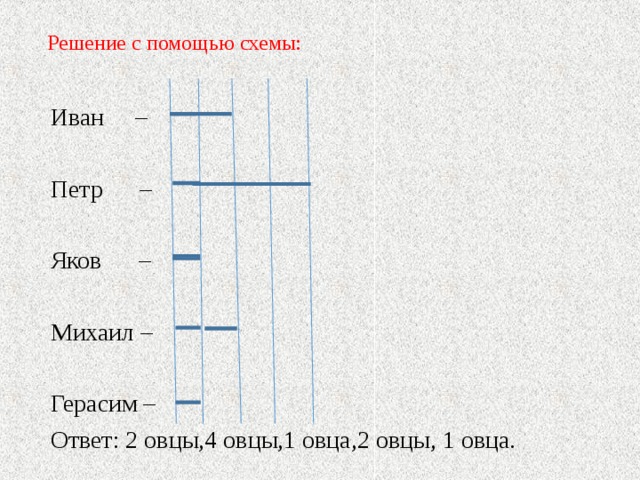
Решение с помощью схемы:

Иван –

Петр –

Яков –

Михаил –

Герасим –

Ответ: 2 овцы,4 овцы,1 овца,2 овцы, 1 овца.

Задача 2 . « На охоте .»

(из книги С.Н. Олехник, Ю.В. Нестеренко, М.К. Потапов

«Старинные занимательные задачи.»)

Пошел охотник на охоту с собакой. Идут они лесом, и вдруг собака увидела зайца. За сколько скачков собака догонит зайца, если расстояние от собаки до зайца равно 40 скачкам собаки и расстояние, которое пробегает собака за 5 скачков, заяц пробегает за 6 скачков?

(В задаче подразумевается, что скачки делаются одновременно и зайцем и собакой.)

Решение, предложенное автором : Если заяц сделает 6 скачков, то и собака сделает 6 скачков, но собака за 5 скачков из 6 пробежит то же расстояние, что заяц за 6 скачков. Следовательно, за 6 скачков собака приблизится к зайцу на расстояние равное одному скачку. Поскольку в начальный момент расстояние между зайцем и собакой было равно 40 скачкам, то собака догонит зайца через 40•6 = 240 скачков.

Решение с помощью уравнения : Пусть х – время погони.

животное

скорость

собака

время погони

5 прыжков

заяц

пройденное расстояние

х

6 прыжков

5х

х

6х

Расстояние пройдено зайцем на 40 прыжков меньше, чем пробежала собака.

Зная, что собака находилась в 40 прыжках от зайца, составим и решим уравнение:

6х = 5х + 40;

х= 40;

5•40 + 40 = 240(скачков).

Ответ : 240 скачков

Задача 3 . « На мельнице.»

На мельнице имеется три жернова. На первом из них за сутки можно смолоть 60 четвертей зерна, на втором 54 четверти, а на третьем 48 четвертей. Некто хочет смолоть 81 четверть зерна за наименьшее время на этих трех жерновах.

За какое наименьшее время можно смолоть зерно и сколько для этого на каждый жернов надо зерна насыпать?

Решение, предложенное автором :

Ясно, что все три жернова должны работать одинаковое время, потому что простой любого из 3-х жерновов увеличивает время помола зерна. Поскольку за сутки все три жернова вместе могут смолоть 60+54+48 = 162 четверти зерна, а надо смолоть 81 четверть, то жернова должны работать 12 часов и за это время на первом жернове надо смолоть 30 четвертей, на втором 27 четвертей, а на третьем 24 четверти зерна.

Решение с помощью уравнения : Пусть х часов работают все три жернова вместе

Задача 4 . « Воз сена.»

Лошадь съедает воз сена за месяц,

коза – за два месяца,

овца – за три месяца.

За какое время лошадь, коза и овца вместе съедят такой же воз сена?

Решение, предложенное автором :

Решение с помощью уравнения : Пусть х- часть месяца

Задача 5 « Мальчики и яблоки.»

Трое мальчиков имеют по некоторому количеству яблок.

Первый из мальчиков дает другим столько яблок, сколько

каждый из них имеет. Затем второй мальчик дает двум

другим столько яблок, сколько каждый из них теперь

имеет; в свою очередь и третий дает каждому из двух

других столько, сколько есть у каждого в этот момент.

После этого у каждого из мальчиков оказывается по 8

яблок.

Сколько яблок было вначале у каждого мальчика?

Решение, предложенное автором :

Так как в конце у каждого из мальчиков оказывается по 8 яблок, а непосредственно перед тем третий дал первому и второму столько, сколько они имели, то перед последней передачей яблок первый и второй мальчики имели по 4 яблока, а третий – 16 яблок. Но тогда перед второй передачей первый мальчик имел – 2 яблока, третий 8 яблок, а следовательно, второй мальчик 4+ 2+ 8 = 14 яблок. Таким образом, сначала у второго мальчика было 7 яблок, у третьего 4 яблока, а у первого

2 + 7 + 4 = 13 яблок.

Решение с помощью системы уравнений : Пусть x - яблок у первого мальчика, y - яблок у первого мальчика. z - яблок у первого мальчика.  

Составим систему уравнений и решим ее:

4х - 4у –4 z = 8; х =13

– 2 x + 6у - 2 z =8; у = 7

– x - у + 7 z = 8 z = 4

Ответ : Вначале у каждого мальчика было :

у I - 13 яблок, у II - 7 яблок, у III – 4 яблока.

Задача 6. А.В.Шевкин «Текстовые задачи » Москва «Просвещение» 1997 №190 Из « Всеобщей арифметики» И.Ньютона.

Двенадцать быков съедают 3 югера ( югер –

древняя римская мера площади около 2500 м 2 )

пастбища за 4 недели; 21 бык съедает 10 югеров

такого же пастбища за 9 недель.

Сколько быков съедят траву на 24 югерах пастбища за 18 недель?

Задача интересна тем, что, кроме первоначального запаса травы, нужно учитывать объем травы, прирастающей ежедневно.

Для простоты считается, что первоначальный объем травы на каждом югере одинаков, что трава растет равномерно, т.е. ежедневно прирастает один и тот же объем травы на каждом югере, а каждый бык съедает в день один и тот же одинаковый для всех быков объем травы. Пусть первоначальный запас травы на каждом югере равен t ед. (здесь и далее объем травы измеряется некоторой общей для всех величин единицей). В день вырастает на каждом югере х ед., а 1 бык съедает в день y ед. Пусть b быков за 18 недель съедят всю траву на лугу в 24 югера. На лугу в 3 югера первоначальный запас травы составлял 3 t ед.. выросло за 4 недели 3 13 х ед., весь этот объем травы быки съели. Но 12 быков за 4 недели съели 124 y = 48 y ед. составим уравнение:

3 t + 13 1 /3 х = 48 y .

Заключение:

• Рассматривая решения, предложенные авторами старых учебников, я пришел к выводу, что эти задачи можно решать современными способами.

Результат :

Закончив свой проект хочу сказать, что я познакомился со старинными задачами. Также хотел бы сказать что решение любых задач развивает логику и смекалку, которая понадобится в жизни ,например как мне когда я помогал строить дом моему дяде, который попросил меня помочь ему с чертежами. Я не сразу понял как составить чертёж дома, но полистав учебник геометрии я научился этому. И так мы с вами изучили виды старинных задач, проанализировали содержание задач на прикладной характер и привели примеры старинных задач которые без проблем решили.

Вывод:

«Кто с детских лет занимается математикой, тот развивает внимание, тренирует свой мозг, свою волю, воспитывает настойчивость и упорство в достижении цели».

А. Маркушевич

Так как математика в настоящее время широко проникает в повседневную жизнь, все более внедряется в традиционно далекие от нее области. Компьютеризация общества, внедрение современных информационных технологий требует математической грамотности человека почти на каждом рабочем месте. Это предполагает и конкретные математические знания, и определенный стиль мышления, вырабатываемый математикой. Решение задач различными способами способствует углублению знаний, развитию логического мышления, расширяет кругозор.

Источники информации и литература

Олехник С.Н. Старинные занимательные задачи. Москва. 1988г.

Глейзер Г. И. История математики в школе. М., Просвещение, 1982

Депман И.Я., Виленкин Н.Я. за страницами учебника математики. Пособие для учащихся 5-7 класса средней школы- М.: Просвещение,1989г.

Перельман Я.И. Занимательная алгебра. М.1980г.

Нагибин Ф.Ф., Капин Е.С. Математическая шкатулка. Пособие для учащихся 4-8 класса средней школы.- М.: Просвещение.1988г.

http://kopilkaurokov.ru/

http:// i gr a emsdetmy .ru