Презентация на тему "Замечательные точки и прямые треугольника"

СОДЕРЖАНИЕ

Точка Торричелли

Ортоцентр

Точка пересечения медиан

Прямая Симпсона

Точка пересечения биссектрис

Окружность Эйлера

Точка пересечения серединных перпендикуляров

Для перехода к слайду № 35 ( свойства замечательных точек и прямых треугольника) сделайте клик по кнопке «Треугольник».

Прямая Эйлера

Точки, симметричные ортоцентру относительно сторон треугольника

Точки Фейербаха

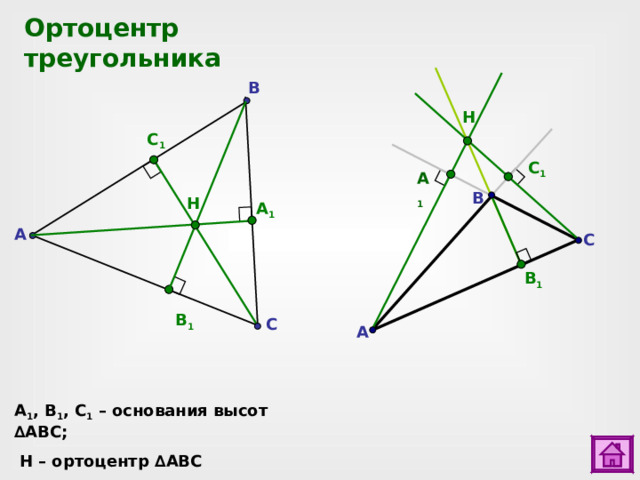
Ортоцентр треугольника

B

H

C 1

C 1

A 1

B

H

A 1

A

C

B 1

B 1

C

A

A 1 , B 1 , C 1 – основания высот ∆ ABC ;

H – ортоцентр ∆ ABC

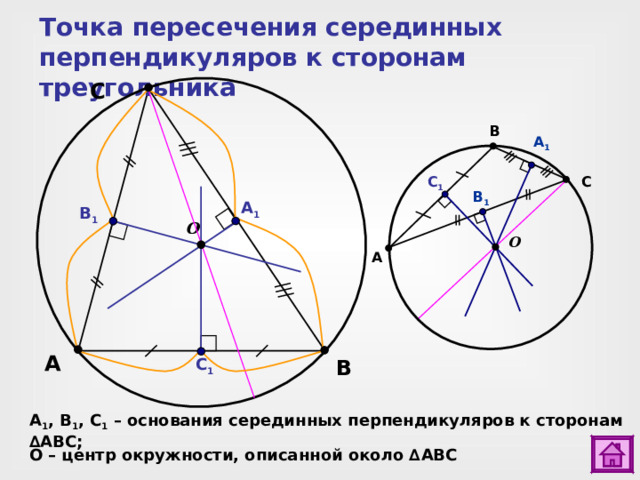
Точка пересечения серединных перпендикуляров к сторонам треугольника

C

B

A 1

C

C 1

B 1

А 1

В 1

О

О

A

A

B

С 1

A 1 , B 1 , C 1 – основания серединных перпендикуляров к сторонам ∆ ABC ;

О – центр окружности, описанной около ∆ ABC

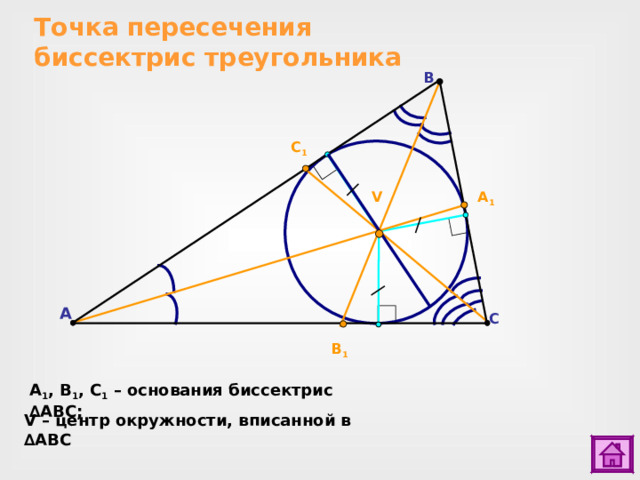
Точка пересечения биссектрис треугольника

B

C 1

V

A 1

A

C

B 1

A 1 , B 1 , C 1 – основания биссектрис ∆ ABC ;

V – центр окружности, вписанной в ∆ ABC

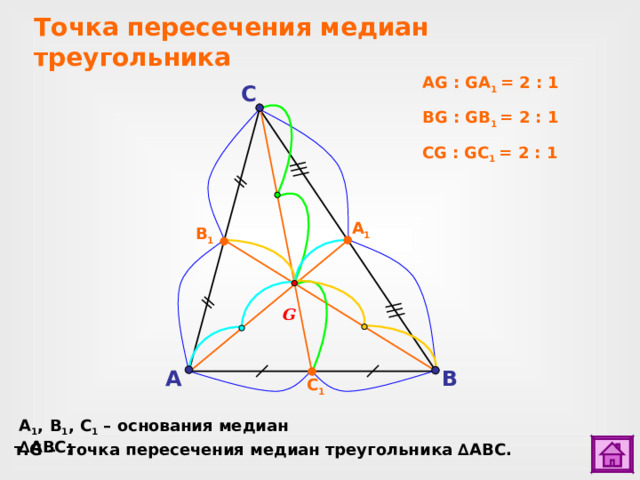
Точка пересечения медиан треугольника

AG : GA 1 = 2 : 1

C

BG : GB 1 = 2 : 1

CG : GC 1 = 2 : 1

А 1

В 1

G

B

A

С 1

A 1 , B 1 , C 1 – основания медиан ∆ ABC ;

т. G – т очка пересечения медиан треугольника ∆ ABC .

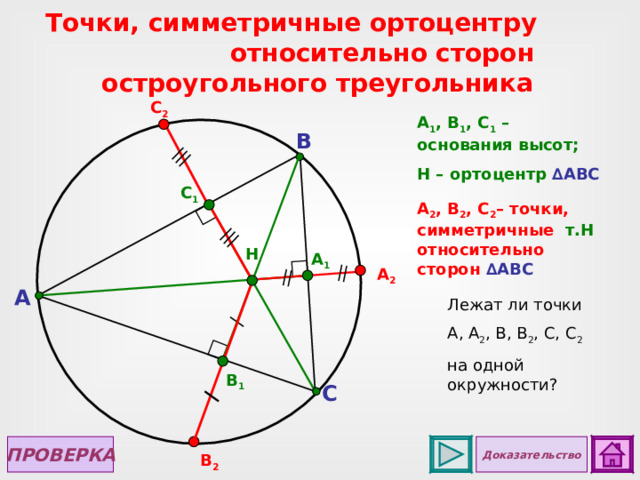
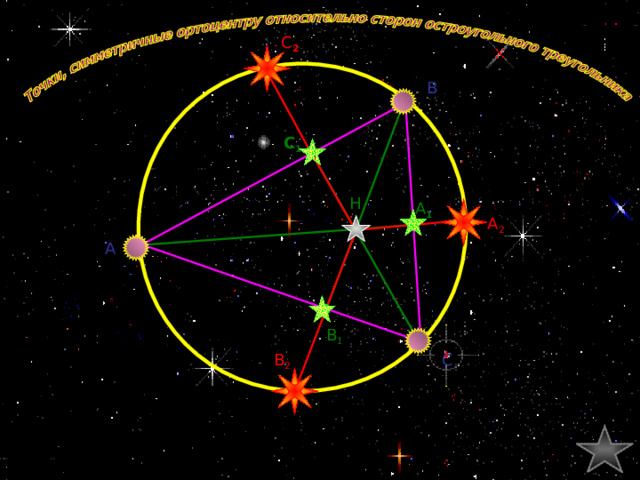
Точки, симметричные ортоцентру относительно сторон остроугольного треугольника

C 2

A 1 , B 1 , C 1 – основания высот;

H – ортоцентр ∆ ABC

B

C 1

A 2 , B 2 , C 2 – точки, симметричные т.Н относительно сторон ∆ ABC

H

A 1

А 2

A

Лежат ли точки

А, А 2 , В, В 2 , С, С 2

на одной окружности?

Для просмотра чертежа в случае с тупоугольным треугольником сделайте клик по управляющей кнопке «Далее».

B 1

C

ПРОВЕРКА

Доказательство

B 2

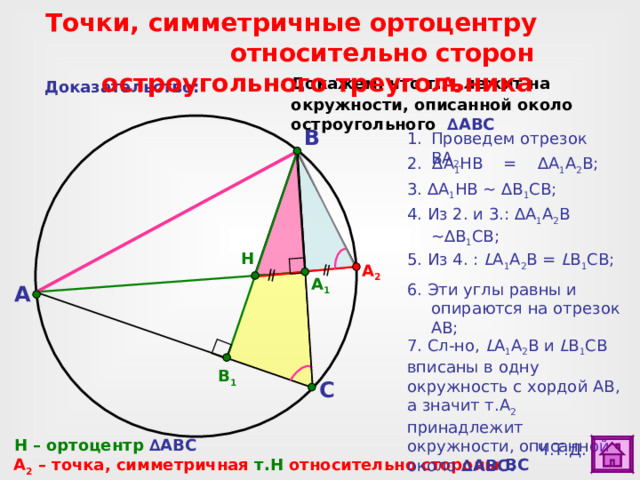
Точки, симметричные ортоцентру относительно сторон остроугольного треугольника

Докажем, что т. А 2 лежит на окружности, описанной около остроугольного ∆ ABC

Доказательство:

B

• Проведем отрезок ВА 2.

2. ∆ A 1 HB = ∆ A 1 A 2 В ;

3. ∆ A 1 HB ~ ∆ B 1 СВ ;

4. Из 2. и 3.: ∆ A 1 A 2 В ~ ∆ B 1 СВ;

H

5. Из 4 . : L A 1 A 2 В = L B 1 СВ;

А 2

A 1

6. Эти углы равны и опираются на отрезок АВ;

A

1) ∆ A 1 HB , ∆ A 1 A 2 В и ∆ B 1 СВ можно выделить дополнительно. Для этого сделайте клик по внутренней области треугольника.

2) Для перехода к слайду № 26 сделайте клик по кнопке «астроном».

7. Сл-но , L A 1 A 2 В и L B 1 СВ вписаны в одну окружность с хордой АВ, а значит т.А 2 принадлежит окружности, описанной около ∆ ABC .

B 1

C

H – ортоцентр ∆ ABC

Ч.Т.Д.

A 2 – точка, симметричная т.Н относительно стороны BC

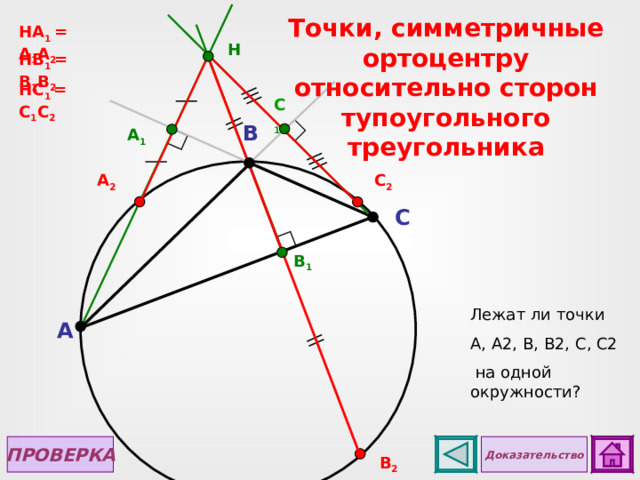
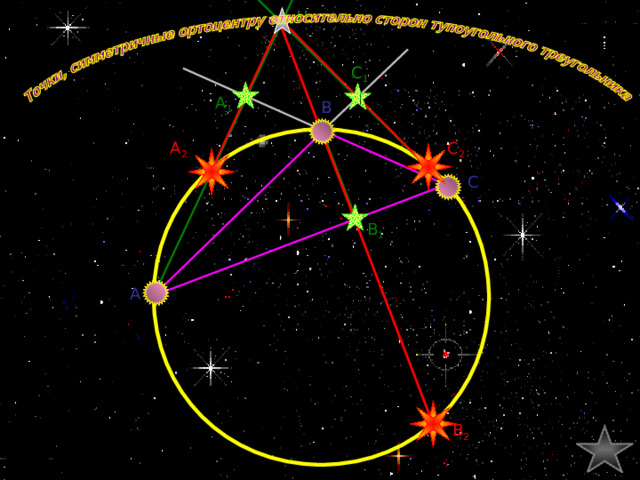
Точки, симметричные ортоцентру относительно сторон тупоугольного треугольника

НА 1 = А 1 А 2

H

Н B 1 = B 1 B 2

Н C 1 = C 1 C 2

C 1

B

A 1

C 2

А 2

C

B 1

Лежат ли точки

А, А2, В, В2, С, С2

на одной окружности?

Для просмотра чертежа в случае с остроугольным треугольником сделайте клик по управляющей кнопке «Назад».

A

ПРОВЕРКА

Доказательство

В 2

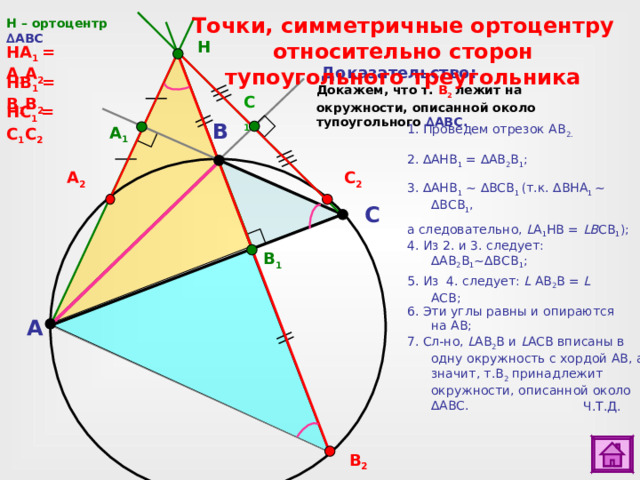
Точки, симметричные ортоцентру относительно сторон тупоугольного треугольника

H – ортоцентр ∆ ABC

H

НА 1 = А 1 А 2

Доказательство:

Н B 1 = B 1 B 2

Докажем, что т. В 2 лежит на окружности, описанной около тупоугольного ∆ ABC .

C 1

Н C 1 = C 1 C 2

B

1. Проведем отрезок АВ 2.

A 1

2. ∆ AHB 1 = ∆ A В 2 В 1 ;

C 2

А 2

3. ∆ AHB 1 ~ ∆ВСВ 1 (т.к. ∆ВНА 1 ~ ∆ B СВ 1 ,

а следовательно, L A 1 НВ = L В СВ 1 );

C

4. Из 2. и 3. следует: ∆ A В 2 В 1 ~ ∆ B СВ 1 ;

B 1

5. Из 4. следует: L A В 2 В = L АСВ;

6. Эти углы равны и опираются на АВ;

1) ∆ A 1 HB , ∆ A В 1 В 2 и ∆ B 1 СВ можно выделить дополнительно. Для этого сделайте клик по внутренней области треугольника.

2) Для перехода к слайду № 27 сделайте клик по кнопке «астроном».

A

7. Сл-но , L A В 2 В и L АСВ вписаны в одну окружность с хордой АВ, а значит, т.В 2 принадлежит окружности, описанной около ∆А B С.

Ч.Т.Д.

В 2

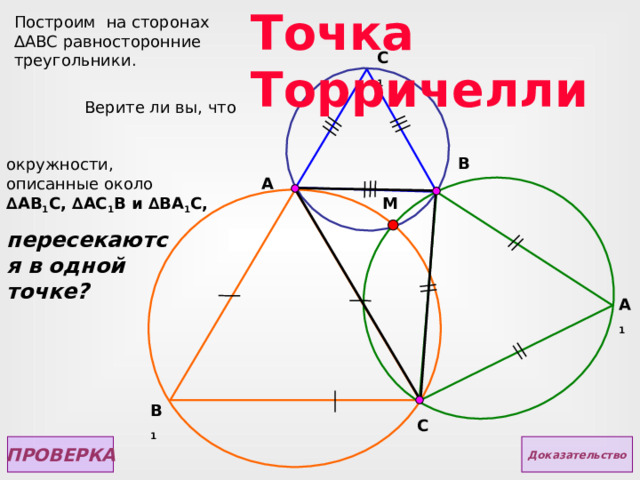
Точка Торричелли

Построим на сторонах ∆АВС равносторонние треугольники.

C 1

Верите ли вы, что

B

окружности, описанные около ∆ AB 1 C, ∆ AC 1 В и ∆ B А 1 C ,

A

M

пересекаются в одной точке?

A 1

B 1

C

ПРОВЕРКА

Доказательство

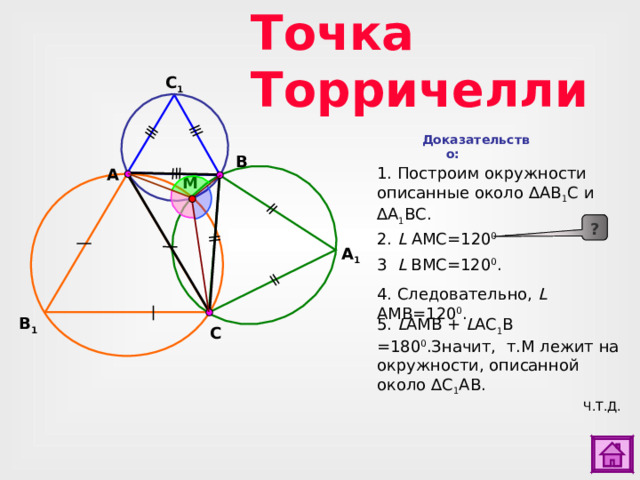
Точка Торричелли

C 1

Доказательство:

B

1 . Построим окружности описанные около ∆АВ 1 С и ∆А 1 ВС.

A

M

?

2. L AMC =120 0

A 1

3 L BMC =120 0 .

4. Следовательно, L AMB =120 0 .

• Для доказательства пункта 2. сделайте клик по кнопке «?»..

2) Для перехода к слайду № 28 сделайте клик по кнопке «астроном».

B 1

5. L AMB + L A С 1 B =180 0 .Значит, т.М лежит на окружности, описанной около ∆ С 1 АВ.

C

Ч.Т.Д.

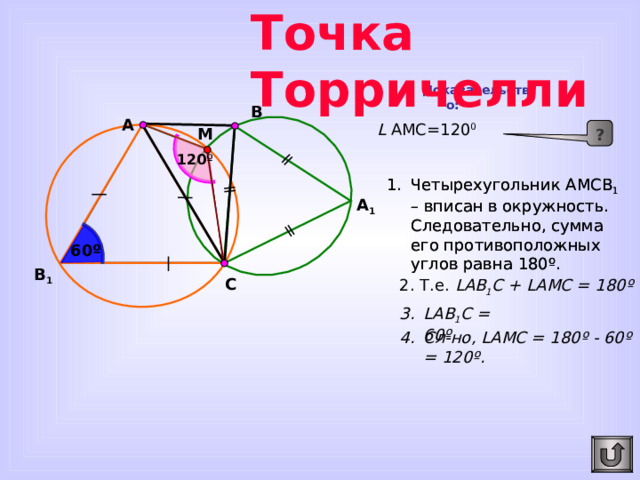
Точка Торричелли

Доказательство:

B

A

L AMC =120 0

?

M

120 º

• Четырехугольник АМСВ 1 – вписан в окружность. Следовательно, сумма его противоположных углов равна 180 º .

• Четырехугольник АМСВ 1 – вписан в окружность. Следовательно, сумма его противоположных углов равна 180 º .

A 1

60 º

B 1

C

2. Т.е. L АВ 1 С + L А M С = 180 º

• L АВ 1 С = 60 º

Для перехода к предыдущему слайду сделайте клик по управляющей кнопке «Возврат».

• Сл-но, L А M С = 180 º - 60 º = 120 º .

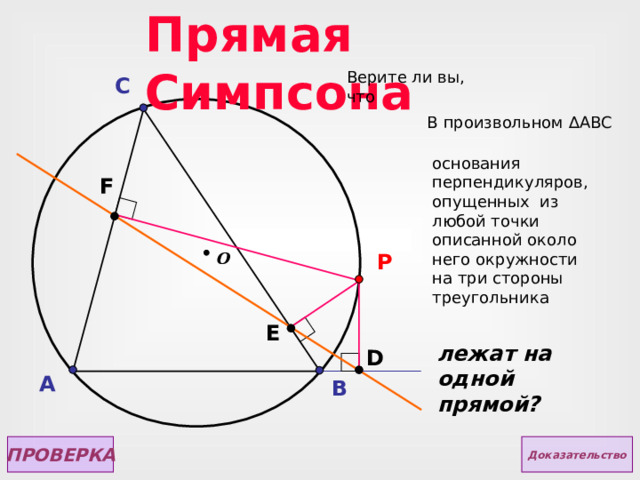
Прямая Симпсона

Верите ли вы, что

C

В произвольном ∆ АВС

основания перпендикуляров, опущенных из любой точки описанной около него окружности на три стороны треугольника

F

P

О

E

лежат на одной прямой?

D

A

B

ПРОВЕРКА

Доказательство

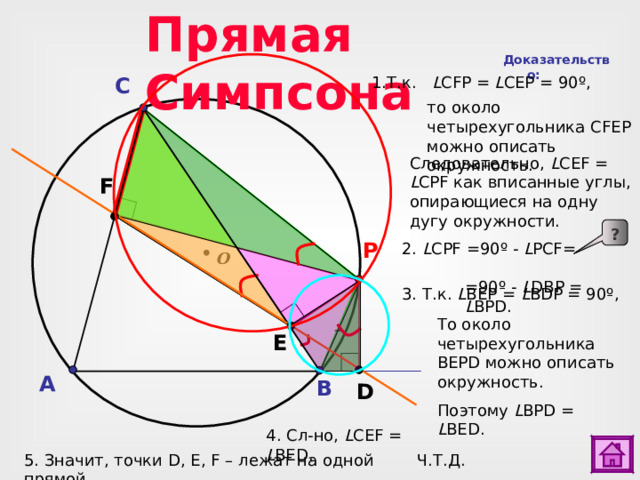
Прямая Симпсона

Доказательство:

1.Т.к. L CFP = L CEP = 90 º ,

C

то около четырехугольника CF Е P можно описать окружность.

Следовательно, L CEF = L CPF как вписанные углы, опирающиеся на одну дугу окружности.

F

?

P

2. L CPF =90 º - L PCF= = 90º - L DBP = L BPD.

О

3. Т.к. L BEP = L BDP = 90 º,

• Для доказательства пункта 2. сделайте клик по кнопке «?»..

2) Для перехода к слайду № 29 сделайте клик по кнопке «астроном».

То около четырехугольника BEPD можно описать окружность.

E

A

B

D

Поэтому L BPD = L BED.

4 . Сл-но, L CEF = L BED.

5. Значит, точки D , E , F – лежат на одной прямой.

Ч.Т.Д.

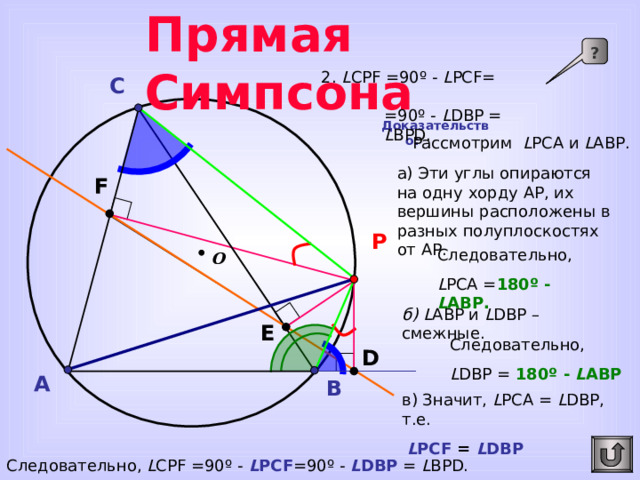
Прямая Симпсона

?

2. L CPF =90 º - L PCF= = 90º - L DBP = L BPD.

C

Доказательство:

Рассмотрим L PC А и L А BP.

а) Эти углы опираются на одну хорду AP , их вершины расположены в разных полуплоскостях от AP .

F

P

Следовательно,

L PC А = 180 º - L А BP .

О

б) L А BP и L DBP – смежные.

Для перехода к предыдущему слайду сделайте клик по управляющей кнопке «Возврат».

E

Следовательно,

L DBP = 180 º - L А BP

D

A

B

в) Значит, L PC А = L DBP , т.е.

L PCF = L DBP

Следовательно, L CPF =90 º - L PCF =90º - L DBP = L BPD.

- середины его сторон А 1 , В 1 , С 1 ;

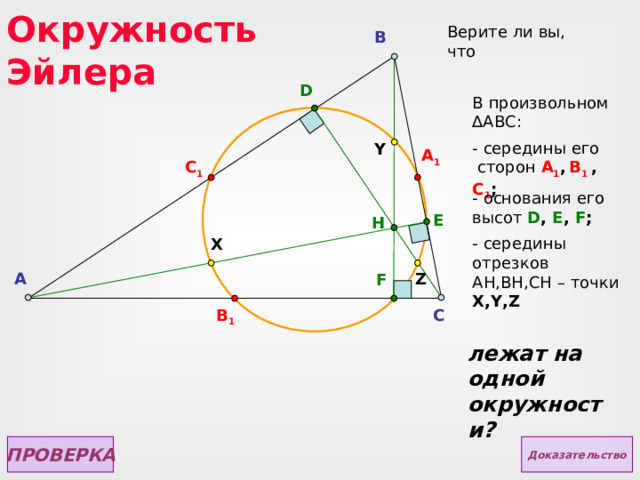
Окружность Эйлера

Верите ли вы, что

B

D

В произвольном ∆ АВС:

Y

A 1

C 1

- основания его высот D , E , F ;

E

H

- середины отрезков AH,BH,CH – точки X,Y,Z

X

Z

A

F

B 1

C

лежат на одной окружности?

ПРОВЕРКА

Доказательство

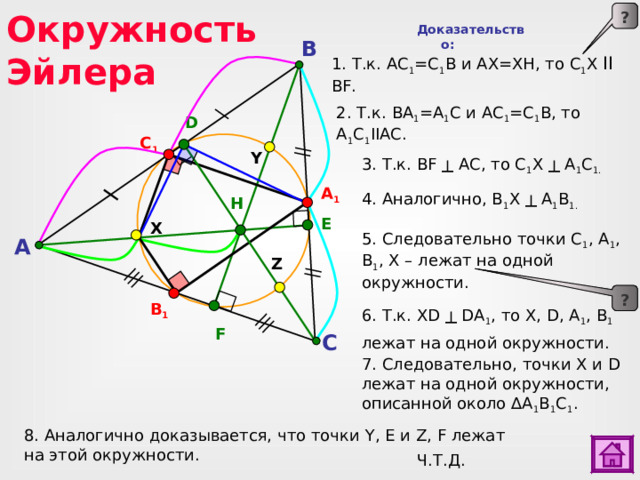
Окружность Эйлера

?

Доказательство:

B

1. Т.к. АС 1 =С 1 В и АХ=ХН, то С 1 Х II BF .

2 . Т.к. ВА 1 =А 1 С и АС 1 =С 1 В, то А 1 С 1 IIAC .

D

C 1

3 . Т.к. BF ┴ AC , то С 1 Х ┴ А 1 С 1.

Y

4. Аналогично, В 1 Х ┴ А 1 В 1.

A 1

H

E

X

5. Следовательно точки С 1 , А 1 , В 1 , Х – лежат на одной окружности.

A

Z

6. Т.к. XD ┴ DA 1 , то X , D , A 1 , B 1 лежат на одной окружности.

?

B 1

• Для доказательства пунктов 2 и 5. сделайте клик по соответствующей кнопке «?»..

2) Для перехода к слайду № 30 сделайте клик по кнопке «астроном».

F

C

7. Следовательно, точки X и D лежат на одной окружности, описанной около ∆ А 1 В 1 С 1 .

8. Аналогично доказывается, что точки Y , E и Z , F лежат на этой окружности.

Ч.Т.Д.

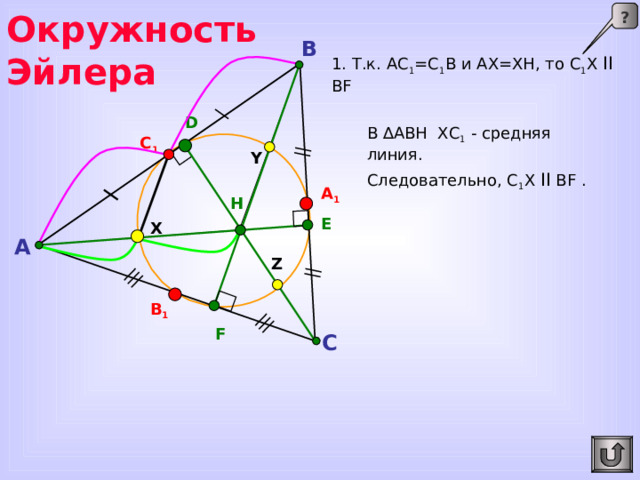
Окружность Эйлера

?

B

1. Т.к. АС 1 =С 1 В и АХ=ХН, то С 1 Х II BF

D

В ∆ АВН ХС 1 - средняя линия.

C 1

Y

Следовательно, С 1 Х II BF .

A 1

H

E

X

A

Z

B 1

Для перехода к предыдущему слайду сделайте клик по управляющей кнопке «Возврат».

F

C

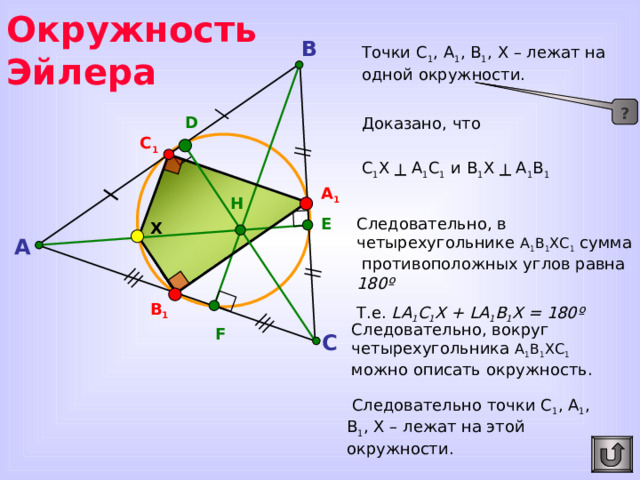
Окружность Эйлера

B

Точки С 1 , А 1 , В 1 , Х – лежат на одной окружности.

?

D

Доказано, что

С 1 Х ┴ А 1 С 1 и В 1 Х ┴ А 1 В 1

C 1

A 1

H

Следовательно, в четырехугольнике А 1 В 1 ХС 1 сумма противоположных углов равна 180 º

Т.е. L А 1 С 1 Х + L А 1 В 1 Х = 180 º

E

X

A

B 1

Для перехода к предыдущему слайду сделайте клик по управляющей кнопке «Возврат».

Следовательно, вокруг четырехугольника А 1 В 1 ХС 1 можно описать окружность.

F

C

Следовательно точки С 1 , А 1 , В 1 , Х – лежат на этой окружности.

20

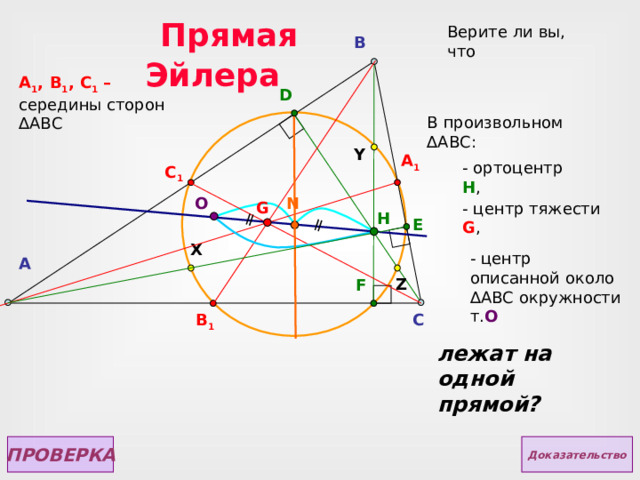
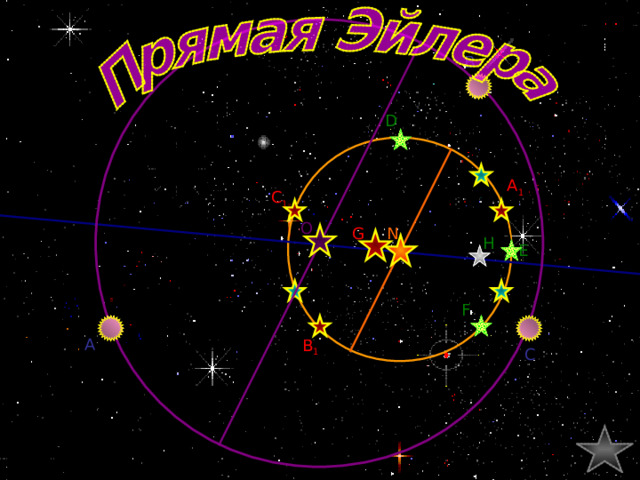
Прямая Эйлера

Верите ли вы, что

B

A 1 , B 1 , C 1 – середины сторон ∆АВС

D

В произвольном ∆ АВС:

Y

A 1

- ортоцентр H ,

C 1

N

O

G

- центр тяжести G ,

H

E

X

- центр описанной около ∆ АВС окружности т. O

A

Z

F

B 1

C

лежат на одной прямой?

ПРОВЕРКА

Доказательство

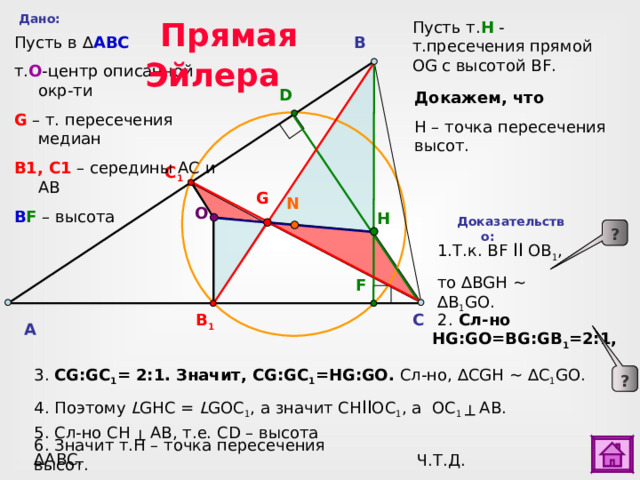
Прямая Эйлера

Дано:

Пусть т. Н - т.пресечения прямой OG с высотой BF.

Пусть в ∆ АВС

т. O -центр описанной окр-ти

G – т. пересечения медиан

В1, С1 – середины АС и АВ

B F – высота

B

D

Докажем, что

Н – точка пересечения высот.

C 1

G

N

О

H

Доказательство:

?

1.Т.к. BF II OB 1 ,

то ∆ BGH ~ ∆ B 1 GO .

F

• Для доказательства пунктов 1 и 2. сделайте клик по соответствующей кнопке «?»..

2) Для перехода к слайду № 31 сделайте клик по кнопке «астроном».

2. Сл-но HG : GO=BG : GB 1 = 2:1,

B 1

C

A

3. CG : GC 1 = 2:1. Значит, CG : GC 1 =HG : GO . Сл-но, ∆С GH ~ ∆С 1 GO .

?

4. Поэтому L GH С = L GO С 1 , а значит СН II OC 1 , а ОС 1 ┴ АВ .

5. C л-но СН ┴ АВ, т.е. CD – высота ∆А B С.

6. Значит т.Н – точка пересечения высот.

Ч.Т.Д.

20

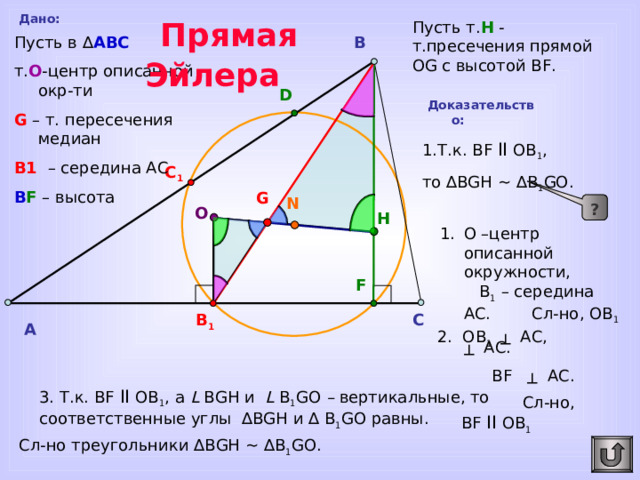
Прямая Эйлера

Дано:

Пусть т. Н - т.пресечения прямой OG с высотой BF.

Пусть в ∆ АВС

т. O -центр описанной окр-ти

G – т. пересечения медиан

В1 – середина АС

B F – высота

B

D

Доказательство:

1.Т.к. BF II OB 1 ,

то ∆ BGH ~ ∆ B 1 GO.

C 1

G

N

?

О

H

• О –центр описанной окружности, В 1 – середина АС. Сл-но, ОВ 1 ┴ АС.

F

Для перехода к предыдущему слайду сделайте клик по управляющей кнопке «Возврат».

B 1

C

2. ОВ 1 ┴ АС, BF ┴ АС. Сл-но, BF II OB 1

A

3. Т.к. BF II OB 1 , а L BGH и L B 1 GO – вертикальные, то соответственные углы ∆ BGH и ∆ B 1 GO равны.

Сл-но треугольники ∆ BGH ~ ∆ B 1 GO .

20

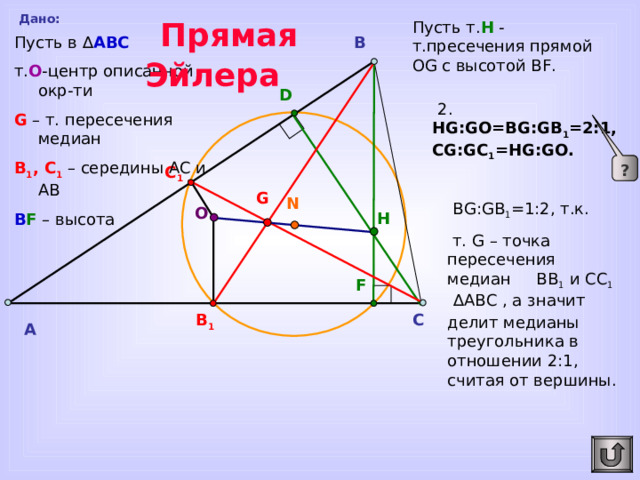
Прямая Эйлера

Дано:

Пусть т. Н - т.пресечения прямой OG с высотой BF.

Пусть в ∆ АВС

т. O -центр описанной окр-ти

G – т. пересечения медиан

В 1 , С 1 – середины АС и АВ

B F – высота

B

D

2. HG : GO=BG : GB 1 = 2:1, CG : GC 1 =HG : GO .

?

C 1

G

N

BG : GB 1 =1 :2, т.к.

т. G – точка пересечения медиан ВВ 1 и СС 1 ∆А B С , а значит делит медианы треугольника в отношении 2:1, считая от вершины.

О

H

F

Для перехода к предыдущему слайду сделайте клик по управляющей кнопке «Возврат».

C

B 1

A

20

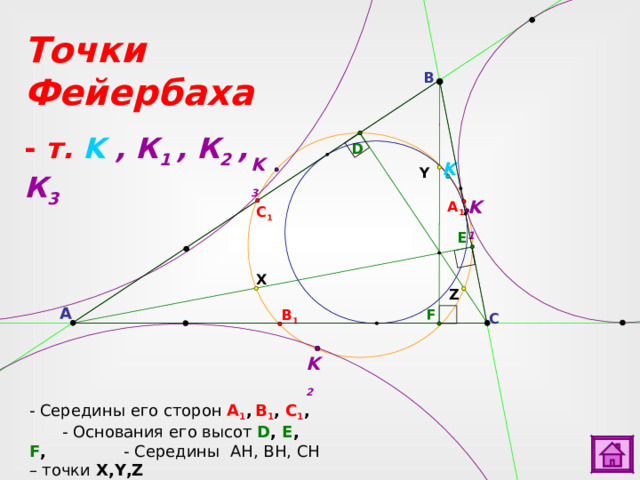
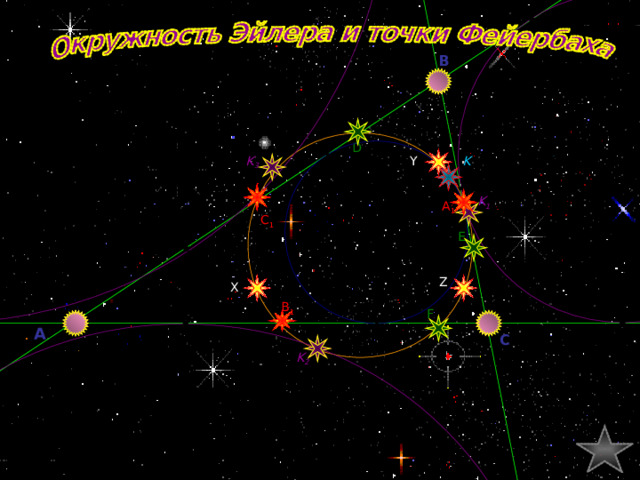
Точки Фейербаха

- т. K , К 1 , К 2 , К 3

B

D

K 3

K

Y

K 1

A 1

C 1

E

X

Z

A

F

B 1

Для перехода к слайду № 32 сделайте клик по кнопке «астроном».

C

K 2

- Середины его сторон А 1 , В 1 , С 1 , - Основания его высот D , E , F , - Середины AH, BH, CH – точки X,Y,Z

20

C 2

B

C 1

H

A 1

А 2

A

Для перехода к предыдущему слайду сделайте клик по управляющей кнопке «Звезда».

B 1

B 2

C

26

H

C 1

A 1

B

C 2

А 2

C

B 1

A

Для перехода к предыдущему слайду сделайте клик по управляющей кнопке «Звезда».

В 2

27

D

A 2

A 1

C

Для перехода к предыдущему слайду сделайте клик по управляющей кнопке «Звезда».

B

A 3

27

C

F

P

О

E

Для перехода к предыдущему слайду сделайте клик по управляющей кнопке «Звезда».

D

A

B

27

B

D

C 1

Y

A 1

H

X

E

A

Z

Для перехода к предыдущему слайду сделайте клик по управляющей кнопке «Звезда».

B 1

F

C

30

B

D

Y

A 1

C 1

O

N

G

H

E

X

Z

F

Для перехода к предыдущему слайду сделайте клик по управляющей кнопке «Звезда».

A

B 1

C

30

B

D

K

K 3

Y

Y

K 1

A 1

C 1

E

X

Z

X

Z

B 1

F

Для перехода к предыдущему слайду сделайте клик по управляющей кнопке «Звезда».

A

C

K 2

32

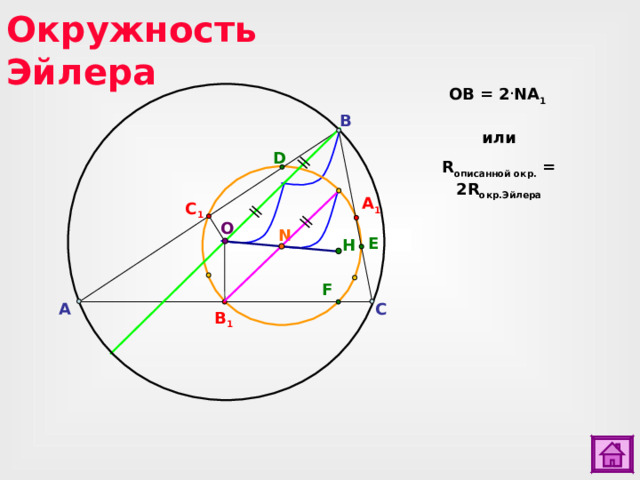
Окружность Эйлера

OB = 2 . NA 1

B

или

R описанной окр. = 2 R окр.Эйлера

D

A 1

C 1

O

N

E

H

F

A

C

B 1

• Для доказательства пунктов 2 и 5. сделайте клик по соответствующей кнопке «?»..

2) Для перехода к слайду № 32 сделайте клик по кнопке «астроном».

32

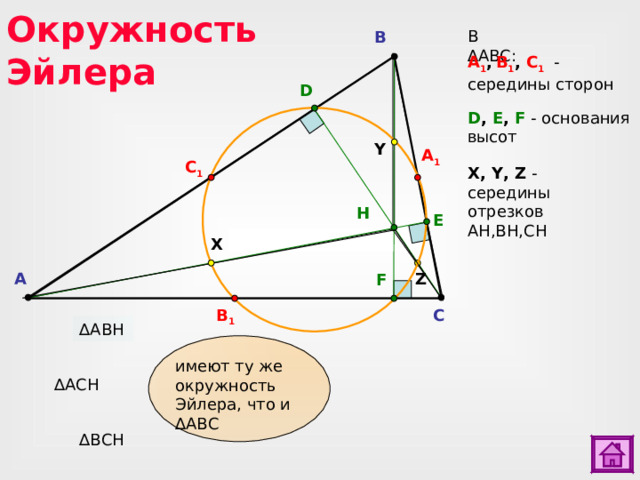
А 1 , В 1 , С 1 - середины сторон

Окружность Эйлера

В ∆ АВС:

B

D

D , E , F - основания высот

Y

A 1

C 1

X, Y, Z - середины отрезков AH,BH,CH

H

E

X

Z

A

F

B 1

C

∆ АВ H

имеют ту же окружность Эйлера, что и ∆АВС

∆ АС H

∆ ВС H

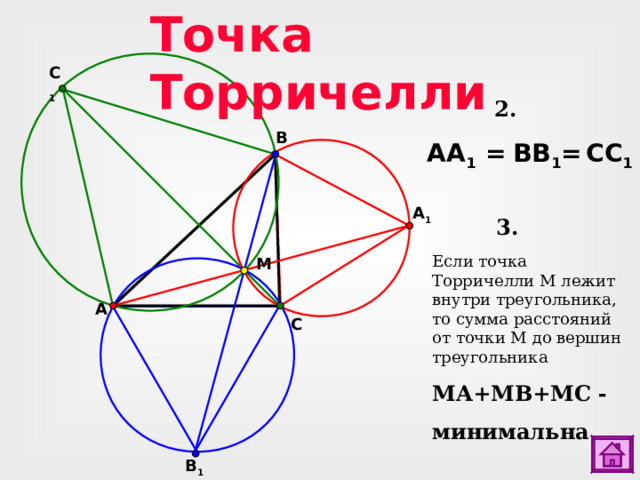
Точка Торричелли

C 1

2.

B

=

CC 1

BB 1

AA 1

=

A 1

3.

Если точка Торричелли М лежит внутри треугольника, то сумма расстояний от точки М до вершин треугольника

M А+ M В+ M С -

минимальна

M

A

C

B 1

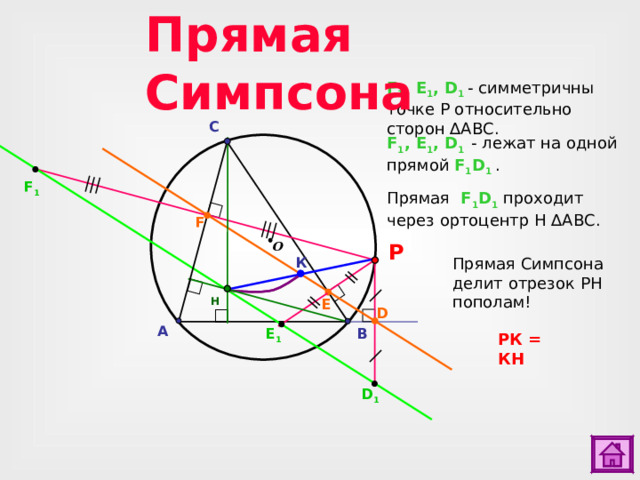
Прямая Симпсона

F 1 , E 1 , D 1 - симметричны точке Р относительно сторон ∆АВС.

C

F 1 , E 1 , D 1 - лежат на одной прямой F 1 D 1 .

F 1

Прямая F 1 D 1 проходит через ортоцентр Н ∆АВС.

F

О

P

Прямая Симпсона делит отрезок РН пополам!

К

H

E

D

A

E 1

B

РК = КН

D 1

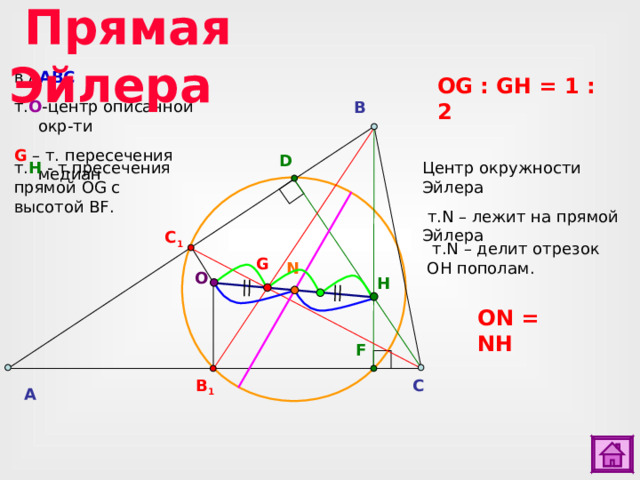
Прямая Эйлера

в ∆ АВС

т. О -центр описанной окр-ти

G – т. пересечения медиан

OG : GH = 1 : 2

B

D

Центр окружности Эйлера

т. N – лежит на прямой Эйлера

т. Н - т.пресечения прямой OG с высотой BF.

C 1

т. N – делит отрезок OH пополам.

G

N

O

H

ON = NH

F

B 1

C

A

34