Презентация к уроку "Решение систем линейных уравнений методом сложения"

Решение систем линейных уравнений методом сложения

Учитель математики

МАОУ гимназии №25 г.Краснодара

Найда С.Н.

Решение систем линейных уравнений методом сложения

Алгебра. 7 класс

Решить систему уравнений с двумя переменными – это значит найти такую пару чисел, которая будет являться решением и первого, и второго уравнения одновременно.

Методы решения систем линейных уравнений:

1. Графический;

2. Подстановки;

3. Сложения.

2x + 4x = 7 + 5

6x = 12

x = 2

4·2 + 5y = 5

5y = -3

y = - 0,6 Ответ: ( 2; -0,6)

Если обе части уравнения умножить или разделить на одно и то же, не равное 0 число, то получим уравнение, равносильное данному.

-6у -8у = 24 -10

-14у = 14

у = -1

9х – 8 =10

х = 2 Ответ: (2; -1).

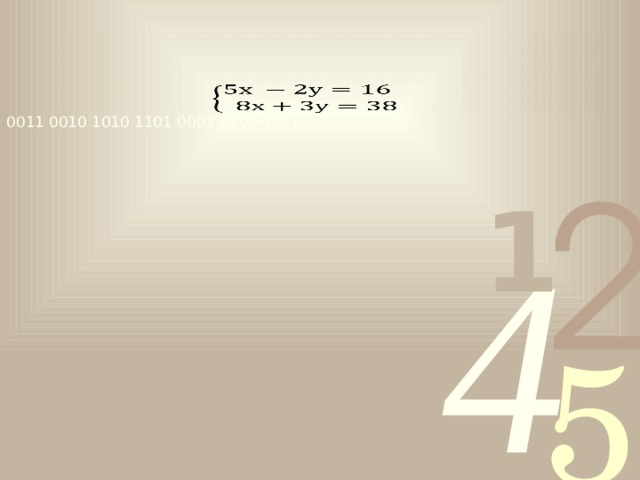
31х = 124

х = 4

5 ·4 -2у =16

-2у = -4

у = 2 Ответ: (4; 2)

Алгоритм решения системы линейных уравнений методом сложения:

• Подобрав «выгодные» множители, преобразовать одно или оба уравнения системы так, чтобы коэффициенты при одной из переменных стали противоположными числами;
• Сложить почленно левые и правые части уравнений;
• Решить полученное уравнение с одной переменной;
• Подставить найденное значение переменной в любое уравнение исходной системы;
• Вычислить значение второй переменной;
• Записать ответ.