Презентация к уроку геометрии 9 класс "Теорема синусов"

Урок геометрии. Тема «Теорема синусов»

Учитель математики МОУ Китовская СШ

Коровкина Надежда Михайловна

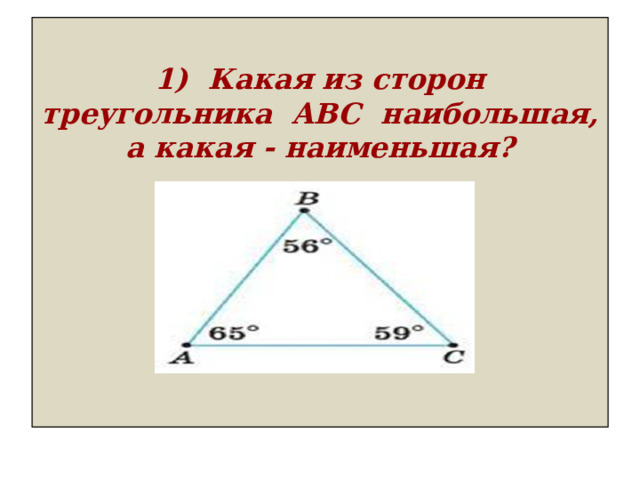
1) Какая из сторон треугольника  ABC  наибольшая, а какая - наименьшая?

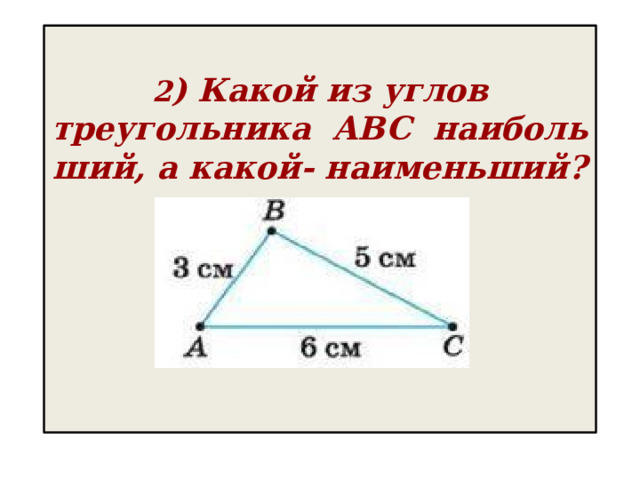
2 ) Какой из углов треугольника  ABC  наибольший, а какой- наименьший?

Проблемная ситуация. Найти расстояние от точки A до недоступной точки B, если

АС = 50 м,  ∠ CAB  = 80 ° и  ∠ ACB  = 72 °  

Тема: « Теорема синусов»  

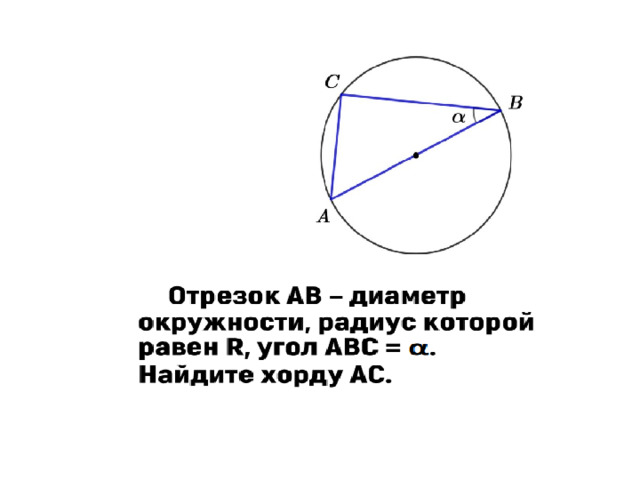
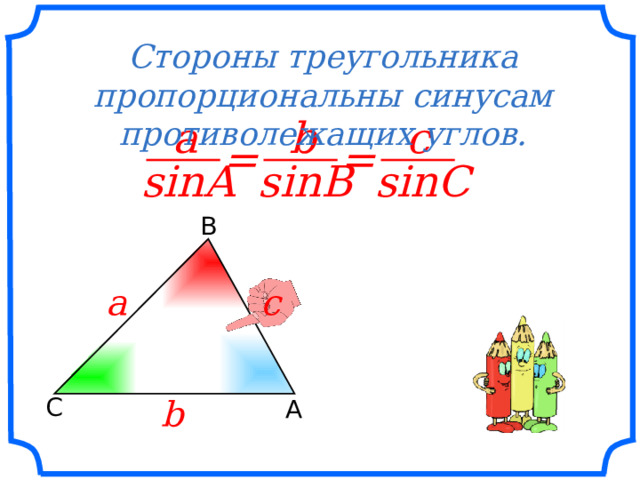
Стороны треугольника пропорциональны синусам противолежащих углов.

b

c

a

=

=

sinB

sinC

sinA

В

c

a

«Геометрия 7-9» Л.С. Атанасян и др.

b

C

A

10

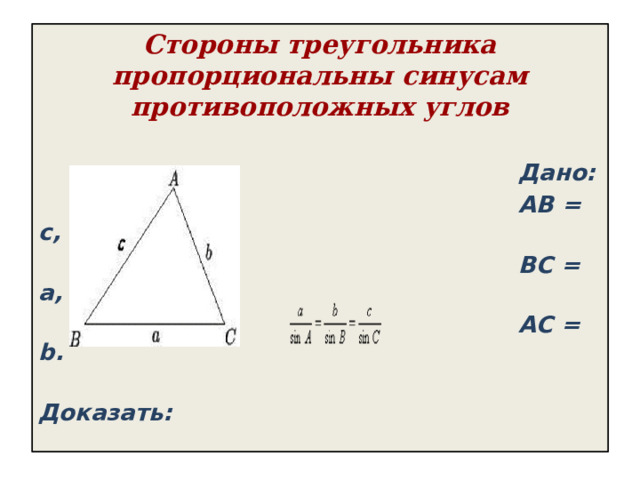
Стороны треугольника пропорциональны синусам противоположных углов

Дано:

AB = c,

BC = a,

AC = b.

Доказать:

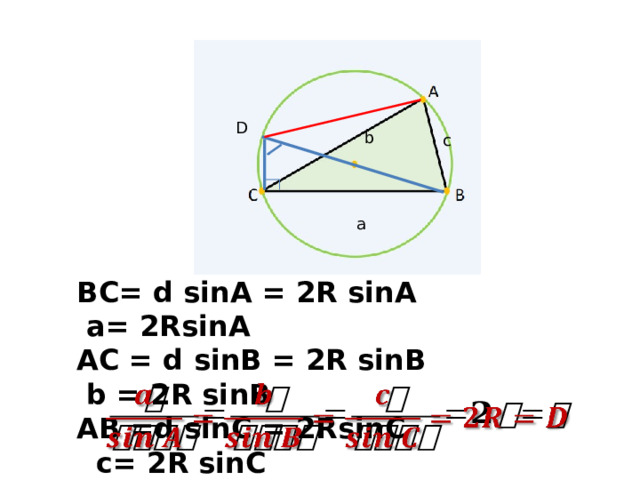
D

b

c

a

BC= d sinA = 2R sinA a= 2RsinA

AC = d sinB = 2R sinB b = 2R sinB

AB =d sinC = 2RsinC c= 2R sinC

Следствие из теоремы синусов

где R – радиус окружности, описанной около ∆ АВС

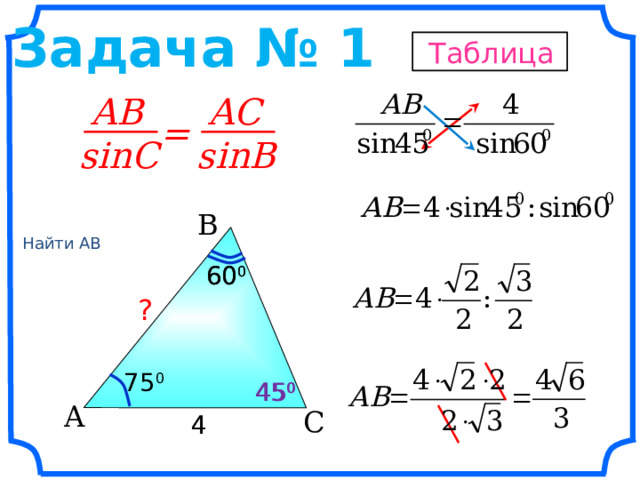
Задача № 1

Таблица

AC

AB

=

sinB

sinC

B

Найти АВ

60 0

60 0

?

Гаврилова Н.Ф. «Поурочные разработки по геометрии: 9 класс». – М.: ВАКО, 2007. – 320 с. – (В помощь школьному учителю)

75 0

45 0

45 0

A

C

4

4

16

Проблемная ситуация. Найти расстояние от точки A до недоступной точки B, если

АС = 50 м,  ∠ CAB  = 80 ° и  ∠ ACB  = 72 °  

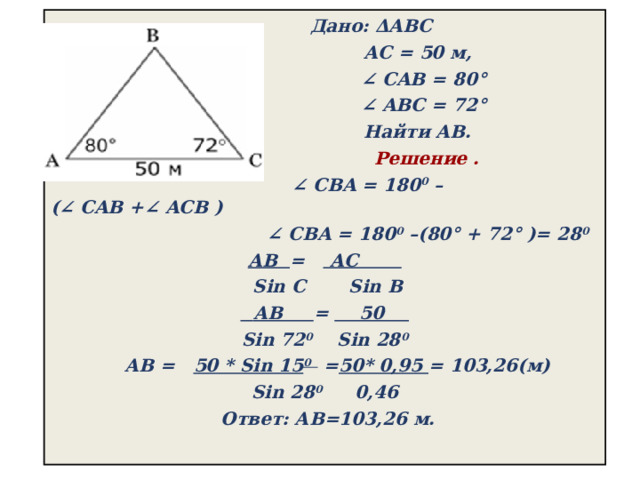
Дано: ΔABC

АС = 50 м, 

∠  CAB = 80° 

∠  ABС = 72° 

Найти AB.

Решение .

∠  CBA = 180 0  –(∠ CAB +∠ ACB )

∠  CBA = 180 0  –(80° + 72° )= 28 0

АВ = АС

Sin C Sin В

АВ = 50

Sin 72 0 Sin 28 0  

АВ = 50 * Sin 15 0 = 50* 0,95 = 103,26(м)

Sin 28 0 0,46

Ответ: АВ=103,26 м.

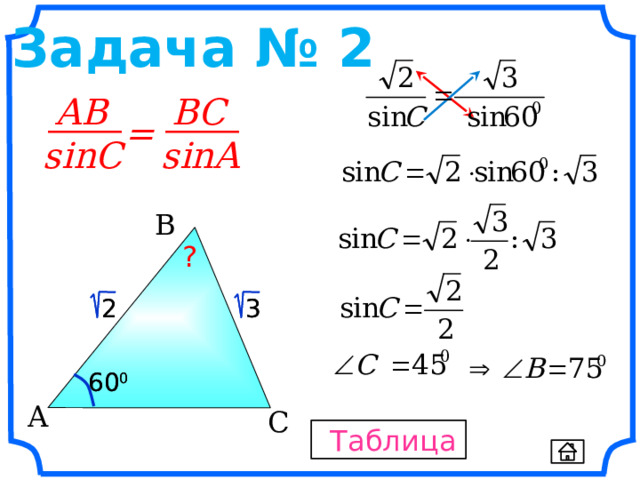
Задача № 2

AB

BC

=

sinC

sinA

B

?

2

3

3

2

Гаврилова Н.Ф. «Поурочные разработки по геометрии: 9 класс». – М.: ВАКО, 2007. – 320 с. – (В помощь школьному учителю)

60 0

60 0

A

C

Таблица

19

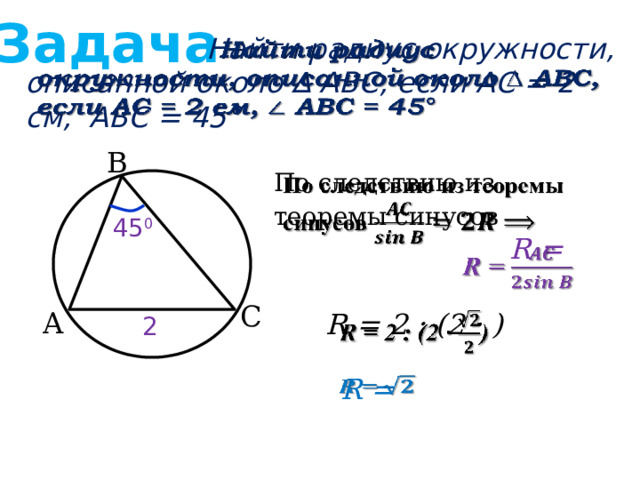
Задача

Найти радиус окружности, описанной около ∆ АВС, если АС = 2 см, АВС = 45°

В

По следствию из теоремы синусов

R =

45 0

С

A

R = 2 : (2 · )

2

R =