Презентация "Интегральное исчисление"

Министерство сельского хозяйства Российской Федерации ФГОУ СПО «Славянский сельскохозяйственный техникум» Электронное учебное пособие Интегральное исчисление

г. Славянск –на- Кубани.

2006г.

Неопределенный интеграл.

1. Сведения из истории о происхождении терминов и обозначений.

2. Интеграл.

3. Дифференциальное и интегральное исчисление.

4. Определение неопределенного интеграла.

5. Геометрический смысл неопределенного интеграла.

6. Основные свойства неопределённого интеграла.

7. Таблица интегралов основных элементарных функций.

8. Методы интегрирования.

9. Непосредственное интегрирование.

10. Метод подстановки ( замена переменной).

11. Метод интегрирования по частям.

12. Применение определенного интеграла.

Сведения из истории о происхождении терминов и обозначений.

Интеграл (от лат. I nteger - целый)-одно из важнейших понятий математики, возникшее в связи с потребностью,

с одной стороны отыскивать функцию по их производным (Например, находить функцию, выражающую путь , пройденный движущейся точкой, по скорости этой точки,

а с другой – измерять площади, объемы, длины дуг, работу сил за определенный промежуток времени и т. п.

Интеграл

В 1655 году английский математик Д. Валлис в "Арифметике бесконечного" впервые рассматривает определённый интеграл как общий предел верхних и нижних интегральных сумм. Ещё более чётко понятие определённого интеграла встречается в трудах Б.Паскаля . Современное определение предела встречается уже в 1880 году у немецкого математика К.Вейерштрасса.

Символ интеграла "удлинённая буква S" был введён Лейбницем в 1686 году, а сам термин "интеграл" был предложен И. Бернулли в 1696 году и одобрен, хотя и неохотно, Лейбницем, который до этого пользовался выражением "сумма".

Дифференциальное и интегральное исчисление

В 1670 году английскому математику И. Барроу впервые удалось установить чисто геометрически взаимоотношение между проведением касательных и квадратурой (задачей вычисления площади фигур). Ньютон пришёл к понятию производной, исходя из вопросов механики. Свои результаты в этой области он изложил в трактате "Метод флюксий и бесконечных рядов" в 1671 году.

Официальным годом рождения дифференциального исчисления считают 1684 год. В мае этого года была опубликована первая печатная работа, в которой излагаются основные понятия и методы дифференциального исчисления. Это была знаменитая статья Лейбница "Новый метод максимумов и минимумов", опубликованная в лейпцигском журнале.

В 1686 году появилась первая печатная работа по интегральному исчислению - статья Лейбница "О глубокой геометрии и анализе неделимых".

Первый систематический печатный курс дифференциального исчисления опубликовал в 1696 году французский математик Ф. Лопиталь под названием "Анализ бесконечно малых".

Символ ∫ введен Лейбницем . Этот знак является изменением латинской буквы S (первой буквы слова сумма). Само слово интеграл придумал Я. Бернулли (1690г.). Вероятно, оно происходит от латинского integer , которое переводится как приводить в прежнее состояние, восстанавливать. Лейбниц Эйлер

Название первообразная функция заменило более раннее « примитивная функция», которую ввел Лагранж (1 797г.). Само понятие выделил Лейбниц , обозначение ввел К. Фурье (1768-1830), пределы указал уже Эйлер . Ньютон Архимед

Определение неопределенного интеграла.

Функция F(x) в данном промежутке называется первообразной функцией для Функции f(x) или интегралом от f(x) , если во всем этом промежутке f(x) является производной для функции F(x) или, что то же , f(x)dx служит для F(x) дифференциалом F’(x)=f(x) или dF(x)=f(x)dx .

Множество всех первообразных для функции f(x) на промежутке (a;b) называется неопределенным интегралом и обозначается ∫ f(x)dx . Если F(x) первообразная для f(x) , то ∫ f(x)dx = F(x)+c ,

где с-произвольное число, постоянное интегрирование.

f(x) –подынтегральная функция,

x -переменная интегрирования,

символ f(x)dx обозначает совокупность всех

первообразныч функций.

Восстановление функции по ее производной или что тоже самое вычисление неопределенного интеграла по данной подынтегральной функции называется интегрированием этой функции.

• Интегрирование есть операция обратная для производной функции, поэтому правильность нахождения неопределенного интеграла проверка дифференцированием полученного выражения

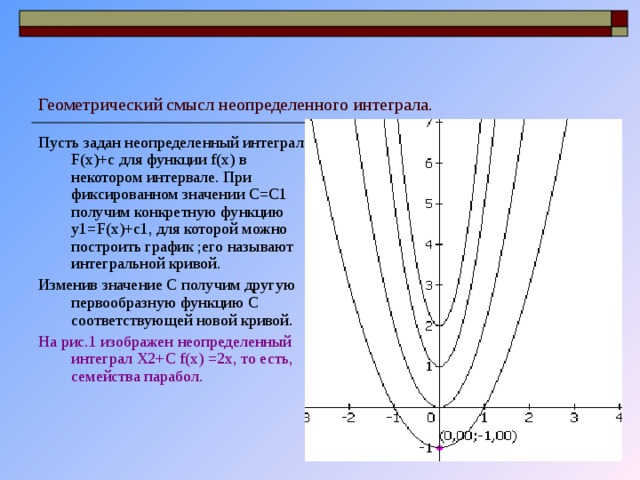
Геометрический смысл неопределенного интеграла.

Пусть задан неопределенный интеграл F(x)+c для функции f(x) в некотором интервале. При фиксированном значении C=C1 получим конкретную функцию y1=F(x)+c1 , для которой можно построить график ;его называют интегральной кривой.

Изменив значение C получим другую первообразную функцию С соответствующей новой кривой.

На рис.1 изображен неопределенный интеграл X2+C f(x) =2x , то есть, семейства парабол.

Основные свойства неопределённого интеграла.

1. Вид неопределённого интеграла не зависит от того, какой

буквой обозначена переменная интегрирования.

∫ 2 x dx = x 2 +c или ∫ 2 t dt = t 2 +c

2. Неопределённый интеграл обладает свойством линейности:

∫ ( k 1 f(x)+k 2 v(x))dx= k 1 ∫ f(x) dx+k 2 ∫ v(x) dx , где k 1 , k 2 = const .

Интеграл от суммы равен сумме интегралов от этих функций и постоянный множитель можно вынести за знак интегралов .

3 . ( ∫ f(x )dx ) ′ =f(x) ,

т.е. производная от неопределенного интеграла по переменной интегрирования равняется подынтегральной функции.

4. ∫ d(f(x))=f(x)+C

5. d ∫ f(x)dx=F(x)dx

Свойства 4 и 5 полезно запоминать так: знаки дифференциала ( d ) и интеграла (∫), стоящие рядом, взаимно уничтожаются( ведь d и

∫ -символы двух взаимнообратных функций.)

Таблица интегралов основных элементарных функций.

Методы интегрирования

• Непосредственное интегрирование
• Метод подстановки ( замена переменной)
• Метод интегрирования по частям

Непосредственное интегрирование

Интегрирование, которое можно произвести с помощью свойств и таблицы интегралов(после преобразования подынтегральных выражений, если необходимо), будем называть непосредственным интегрированием.

Примеры непосредственного интегрирования:

Метод подстановки ( замена переменной)

Суть этого метода состоит в том, чтобы введя новую переменную, получить интеграл, первообразная которого легко находиться. В основном, для каждого конкретного интеграла замена переменной

( подстановка) подбирается индивидуально. Первообразные почти всех рассмотренных ранее интегралов можно найти методом подстановки. Возможности этого метода рассмотрим на примерах.

Метод интегрирования по частям

Если подынтегральная функция является произведением степенной и показательной функции (степенной и тригонометрической, степенной и логарифмической, показательной и степенной и т. п.), то первообразные таких интегралов следует находить по частям, т. е. по формуле

∫ udv=uv- ∫ vdu

Интегрирования по частям

Пример:

Определенный интеграл.

1. Задачи приводящие к понятию определенного интеграла.

2. Определение определенного интеграла.

3. Свойства определенного интеграла.

4. Вычисление определенного интеграла.

5. Формула Ньютона -Лейбница.

6. Замена переменной интегрирования в определенном интеграле.

7. Интегрирование по частям.

8. Применение определенного интеграла к решению прикладных задач.

Задачи приводящие к понятию определенного интеграла.

Задача1.

Пусть материальная точка М движется прямолинейно неравномерно по закону v=v (t) . Найти путь, пройденный точкой за время от T 1 до T 2 .

Рассмотрим частный случай, когда движение равномерно, т.е. V (t)=const=v* .

Решение:

Путь пройденный материальной точкой М за время от T 1 до T 2

определяется по формуле: AB= ∆ S= v*(t 1 –t 2 )= v* ∆ t . Если v=v (t) , т. е. скорость есть функция от времени, то применим идею определенного интегрирования ( суммирования), которая состоит в следующем: Разобьем временной отрезок AB произвольным образом на n отрезков:

Определение определенного интеграла.

Определенным интегралом называется предел , к которому стремится n -я интегральная сумма (А) при стремлении к нулю длины наибольшего частичного интервала.

Замечание. Подразумевается, что этот предел существует и не зависит ни от способа разбиения отрезка [a, b] на n частей, ни от способа выбора точек . Числа А и называется пределами интегрирования ( нижний и верхний).

Формула Ньютона -Лейбница.

Определенный интеграл есть приращение первообразной функции при изменении переменной интегрирования x от a до b .

Формула Ньютона –Лейбница.

Правило: Чтобы вычислить определенный интеграл

достаточно:

1.Найти неопределенный интеграл от данной функции, положив с=0;

2. Подставив в выражение первообразной вместе аргумента x сначала верхний предел b , затем нижний предел a , из первого результата вычесть второй.

Свойства определенного интеграла. Понятие «определенного интеграла»введено для случая» а

. Пусть b

. Если функция f (x) интегрируема на [a, b] , то функция k f (x) , где k –постоянная,

также интегрируема на этом отрезке, при этом

Свойства определенного интеграла. Понятие «определенного интеграла»введено для случая» а

. Если две функции f (x) и g (x) интегрируемы на [a, b] , то их сумма и разность также интегрируема на [a, b] и имеет место равенство

Замена переменной в определенном интеграле производится по формуле

Пример 1 . Найти

1.Находим неопределенный интеграл, полагая с=0. Имеем

2 .Вычисляем приращение первообразной :

При наличии навыка запись решения примера должна выглядеть так:

Пример 2 . Найти

Этот интеграл вычисляется с помощью замены:

И при , а при

Поэтому

Пример3. Найти

Этот интеграл следует вычислять по частям, т.е. по формуле

Пусть

тогда

Поэтому

Приложение определенного интеграла.

1.Площадь плоской фигуры.

2. Вычисление объема тела по известным площадям поперечных сечений.

3.Вычисление объема тела вращения.

4.Работа совершаемая переменной силой.

5.Прирост численной популяции.

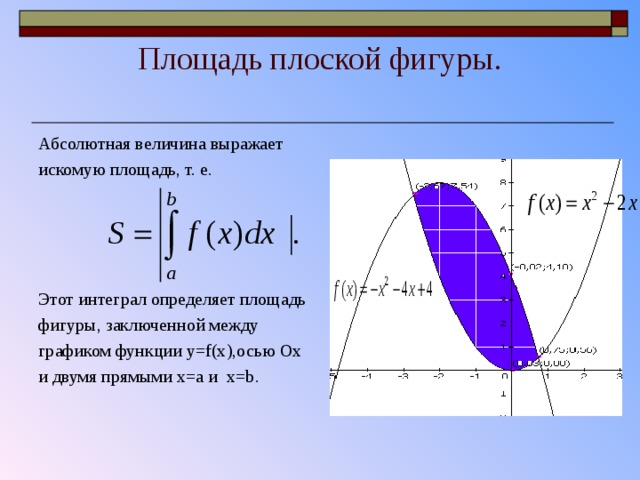
Площадь плоской фигуры.

Абсолютная величина выражает

искомую площадь, т. е.

Этот интеграл определяет площадь

фигуры, заключенной между

графиком функции y=f(x), осью Ox

и двумя прямыми x=a и x=b.

Площадь плоской фигуры.

Если график функции y=f(x) на интервале

[a,b] несколько раз пересекает ось Ox , то

необходимо вычислять площади

фигур, расположенных выше оси Ox , а

также площади фигур, которые

лежат ниже оси Ox , и сложить их

абсолютные величины. Так,

площадь заштрихованной фигуры равна

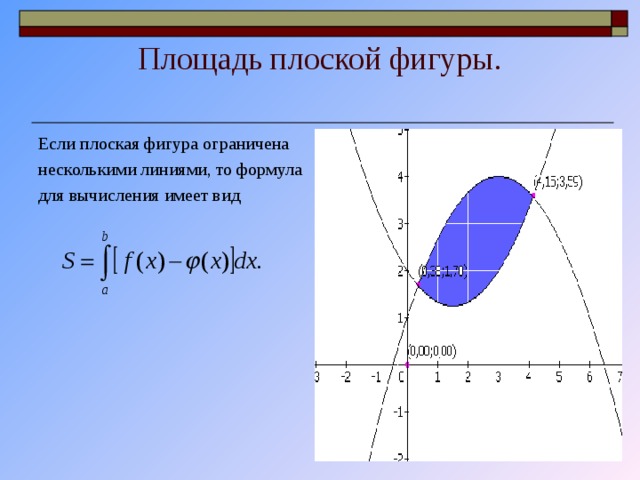
Площадь плоской фигуры.

Если плоская фигура ограничена

несколькими линиями, то формула

для вычисления имеет вид

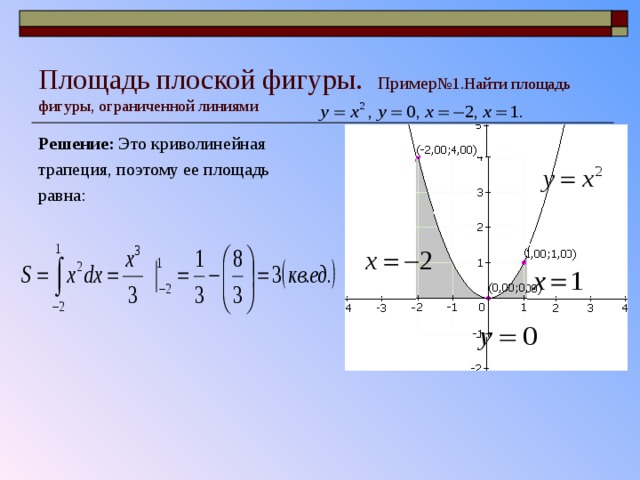
Площадь плоской фигуры. Пример №1.Найти площадь фигуры, ограниченной линиями

Решение: Это криволинейная

трапеция, поэтому ее площадь

равна:

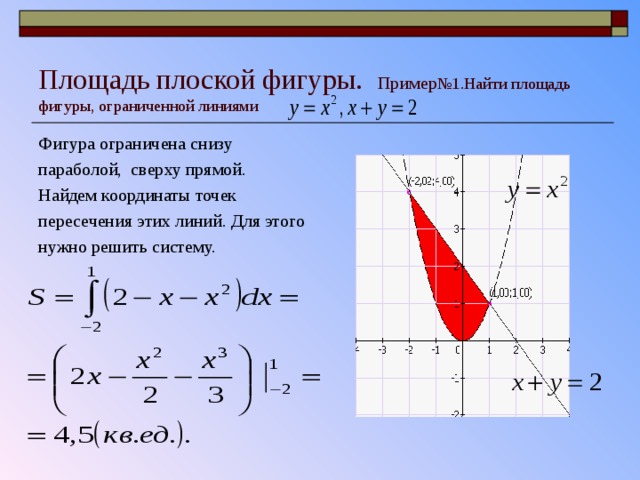
Площадь плоской фигуры. Пример №1.Найти площадь фигуры, ограниченной линиями

Фигура ограничена снизу

параболой, сверху прямой.

Найдем координаты точек

пересечения этих линий. Для этого

нужно решить систему.

Вычисление объема тела по известным площадям поперечных сечений.

Если площадь сечения плоскостью, перпендикулярной оси Ox , может быть выражена как функция от х, т.е. в виде S=S (x) (a

Вычисление объема тела вращения.

Пусть вокруг оси Ox вращается

криволинейная трапеция,

ограниченная линиями:

Тогда объем полученного тела

вращения можно найти по формуле:

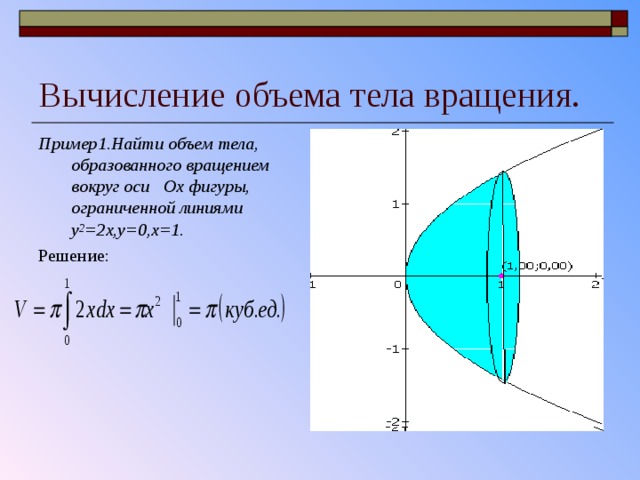
Вычисление объема тела вращения.

Пример1.Найти объем тела, образованного вращением вокруг оси Ox фигуры, ограниченной линиями y 2 =2x,y=0,x=1.

Решение:

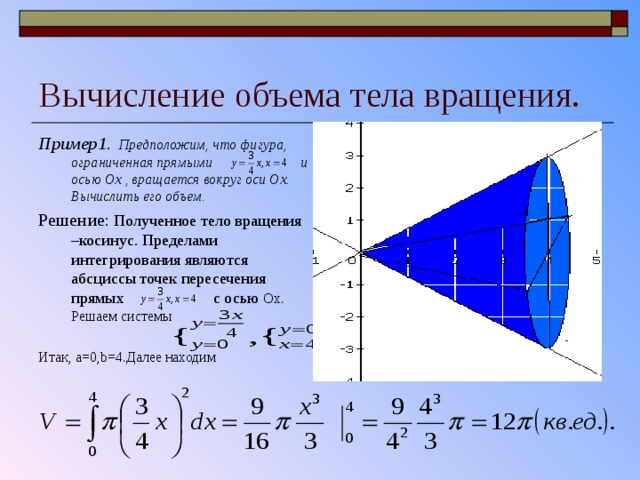
Вычисление объема тела вращения.

Пример1. Предположим, что фигура, ограниченная прямыми и осью Ox , вращается вокруг оси Ox . Вычислить его объем.

Решение: Полученное тело вращения –косинус. Пределами интегрирования являются абсциссы точек пересечения прямых с осью Ox . Решаем системы

Итак, а=0, b=4. Далее находим

Работа совершаемая переменной силой .

Пусть на материальную точку в положительном направлении оси Ox действует сила F(x) , в результате чего точка перемещается из положения х = а

в положение х = b . Найдем совершаемую при этом работу. ( Если величина силы меняется в зависимости от точки приложения, то эта формула непригодна.)

Вывод: Величина работы, совершаемой переменной силой, направление которой совпадает с направлением движения, равна определенному интегралу от величины силы по длине пути.

Работа совершаемая переменной силой .

Пример1. Какую работу надо совершить, чтобы растянуть пружину на 4 см., если известно , что от нагрузки в 1Н она растягивается на 1см?

(См. справочный материал.)

Решение:

Согласно закону Гука , сила Х Н, растягивающая пружина на х м , равна Х= k x. коэффициент пропорциональности k найдем из условия: если х=0,01м, то Х=1Н; следовательно, k =1\0,01=100 и Х=100х. Тогда

Прирост численной популяции.

Пусть известна скорость v (t) роста некоторой популяции. Требуется найти прирост численности за время от до T . Если скорость роста постоянна, то

Прирост популяции равен определенному интегралу от скорости по интервалу времени ее размножения.

Заключение.

Данное методическое пособие может быть использовано преподавателями и студентами при подготовке к занятиям по теме «Интегральное исчисление», а также при проектировании курсовых проектов студентов агрономического и бухгалтерского отделения.