Презентация по математике "Объем шара и площадь сферы"

В работе предоставлен исторический материал.

Формула для вычисления объема шара была открыта древнегреческим ученым Архимедом, который разработал методы нахождения площадей, поверхностей и объемов различных фигур и тел.

Для доказательства теоремы  об объеме шара использовали метод координат, который ввел в геометрию Р. Декарт.

В презентации рассматриваются вопросы:  вывод формулы объема шара, объем шарового сегмента, понятие шарового слоя, площади сферы. Приведены примеры задач на нахождение объема шара.

Архимед

Формула для вычисления объема шара была открыта древнегреческим ученым Архимедом. Родом из Сиракуз (Сицилия). Разработал предвосхитившие интегральное исчисление методы нахождения площадей, поверхностей и объемов различных фигур и тел. В основополагающих трудах по статике и гидростатике (закон Архимеда) дал образцы применения математики в естествознании и технике. Автор многих изобретений (архимедов винт, определение состава сплавов взвешиванием в воде, системы для поднятия больших тяжестей, военные метательные машины).

Объем шара радиуса R равен 4/3ПR³

Объем шара и площадь сферы

Архимед

Формула для вычисления объема шара была открыта древнегреческим ученым Архимедом. Родом из Сиракуз (Сицилия). Разработал предвосхитившие интегральное исчисление методы нахождения площадей, поверхностей и объемов различных фигур и тел. В основополагающих трудах по статике и гидростатике (закон Архимеда) дал образцы применения математики в естествознании и технике. Автор многих изобретений (архимедов винт, определение состава сплавов взвешиванием в воде, системы для поднятия больших тяжестей, военные метательные машины).

Объем шара

Теорема.

Объем шара радиуса R равен

4/3П R 3

Доказательство:

Рассмотрим шар радиуса R с центром в точке О и выберем ось Ох произвольным образом. Сечение шара плоскостью, перпендикулярной к оси Ох и проходящей через точку М этой оси, является кругом с центром в точке М. Обозначим радиус этого круга r площадь через S ( x ). Выразим S ( x ) через x и R . Из прямоугольного треугольника ОМС находим

Р. Декарт

Для доказательства использовали метод координат, который ввел в геометрию Р. Декарт. Декартова система координат, прямолинейная система координат на плоскости или в пространстве (обычно с одинаковыми масштабами по осям). Сам Р. Декарт в "Геометрии" (1637) употреблял только систему координат на плоскости. В математике Декарт первым ввел понятие переменной и функции, заложил основы аналитической геометрии, которые были представлены в его работе «Геометрия» (1637). Переменная величина у Декарта выступала в двойной форме: как отрезок переменной длины и постоянного направления – текущая координата точки, описывающей своим движением кривую, и как непрерывная числовая переменная, пробегающая совокупность чисел, выражающих этот отрезок. Двоякий образ переменной обусловил взаимопроникновение геометрии и алгебры. У Декарта действительное число трактовалось как отношение любого отрезка к единичному, хотя сформулировал такое определение лишь И. Ньютон; отрицательные числа получили у Декарта реальное истолкование в виде направленных ординат. Декарт значительно улучшил систему обозначений, введя общепринятые знаки для переменных величин (x, у, z,...) и коэффициентов (a, b, с,...), а также обозначения степеней (х4, a5,...). Запись формул у Декарта почти ничем не отличается от современной.

Объем шарового сегмента

Шаровым сегментом называется часть шара, отсекаемая от него какой- нибудь плоскостью.

Круг, получившийся в сечении, называется основанием каждого из этих сегментов, а длины отрезков АВ и ВС диаметра АС, перпендикулярного к секущей плоскости, называется высотами сегментов.

V шарового сегмента вычисляется по формуле:

Применяя основную формулу для вычисления объемов тел при а = R - h , b= r, получим

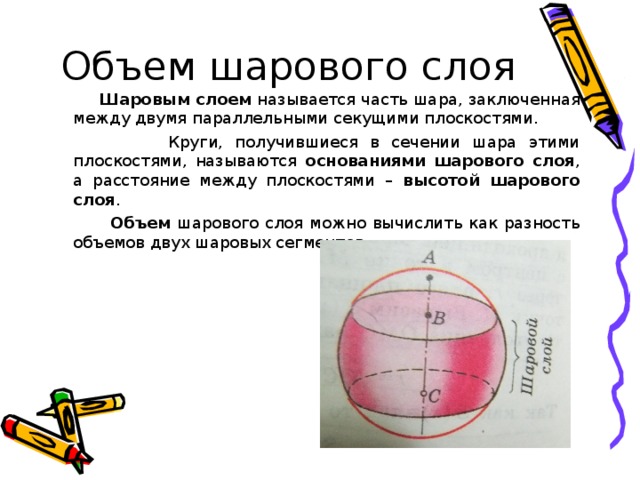
Объем шарового слоя

Шаровым слоем называется часть шара, заключенная между двумя параллельными секущими плоскостями.

Круги, получившиеся в сечении шара этими плоскостями, называются основаниями шарового слоя , а расстояние между плоскостями – высотой шарового слоя .

Объем шарового слоя можно вычислить как разность объемов двух шаровых сегментов.

Объем шарового сектора.

Шаровым сектором называется тело, полученное вращением кругового сектора с углом, меньшим 90, вокруг прямой, содержащей один из ограничивающих круговой сектор радиусов. Шаровой сектор состоит из шарового сегмента и конуса.

V шарового сектора вычисляется по формуле

Площадь сферы

S сферы радиуса R

Рассмотрим сферу радиуса R с центром в точке О и описанный около нее многогранник, имеющий n граней.

Соединив центр О сферы отрезками со всеми вершинами многогранника, получим n пирамид с общей вершиной О, основаниями которых являются грани многогранника, а высоты – радиусы сферы, проведенные в точки касания граней многогранника со сферой.

V всего описанного многогранника равен:

Задача № 1

На надгробном камне могилы Архимеда в Сиракузах изображен цилиндр с вписанным в него шаром. Это символ открытия формул объема шара и площади сферы, а также важного вывода, что «объем шара, вписанного в цилиндр, в … раз меньше объема цилиндра и что также относятся поверхности этих тел».

Найти:

1)отношение объема шара к объему цилиндра;

2)отношение площади шара к площади поверхности цилиндра.

Задача № 2

Из деревянного равностороннего цилиндра выточен наибольший возможный шар. Сколько процентов материала сточено?

Спасибо за внимание! Подготовила учитель математики Радовня Т.Л