Презентация "График линейной функции, его свойства и формулы"

График линейной функции, его свойства и формулы

Понятие функции

Функция  — это зависимость «y» от «x», где «x» является переменной или аргументом функции, а «y» — зависимой переменной или значением функции

Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения

Понятие функции

График функции  — это объединение всех точек, когда вместо «x» можно подставить произвольные значения и найти координаты этих точек

Понятие линейной функции

Линейная функция  — это функция вида y = kx + b , где х — независимая переменная, k, b — некоторые числа

При этом k — угловой коэффициент, b — свободный коэффициент

Если известно конкретное значение х, можно вычислить соответствующее значение у

Понятие линейной функции

Нам дана функция: у = 0,5х - 2. Значит

если х = 0, то у = -2

если х = 2, то у = -1

если х = 4, то у = 0

и т. д.

Понятие линейной функции

Для удобства результаты можно оформлять в виде таблицы

Графиком линейной функции является прямая линия

Для его построения достаточно двух точек , координаты которых удовлетворяют уравнению функции

Угловой коэффициент отвечает за угол наклона прямой, свободный коэффициент — за точку пересечения графика с осью ординат

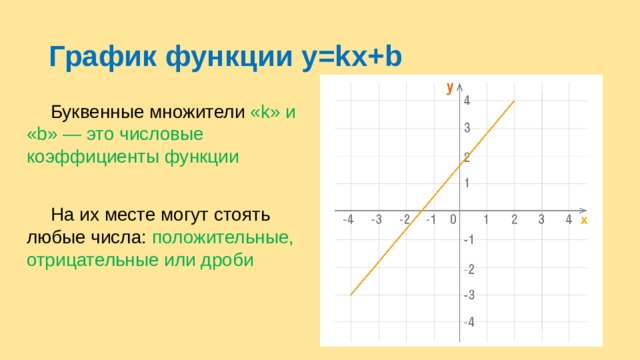
График функции y=kx+b

Буквенные множители «k» и «b» — это числовые коэффициенты функции

На их месте могут стоять любые числа: положительные, отрицательные или дроби

Давайте потренируемся и определим для каждой функций, чему равны числовые коэффициенты «k» и «b»

Может показаться, что в функции « y = 0,2x » нет числового коэффициента «b», но это не так

В данном случае он равен нулю

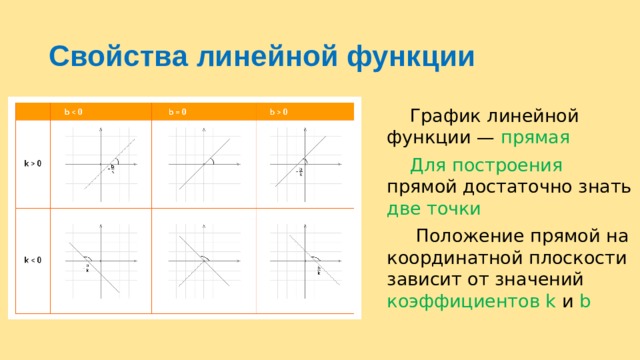
Свойства линейной функции

График линейной функции — прямая

Для построения прямой достаточно знать две точки

Положение прямой на координатной плоскости зависит от значений коэффициентов k и b

0 , то график наклонен вправо если k Коэффициент b отвечает за сдвиг графика вдоль оси OY если b 0 , то график функции y = kx + b получается из y = kx со сдвигом на b единиц вверх вдоль оси OY если b " width="640"

Свойства линейной функции

В уравнении функции y = kx + b коэффициент k отвечает за наклон графика функции

• если k 0 , то график наклонен вправо
• если k

Коэффициент b отвечает за сдвиг графика вдоль оси OY

• если b 0 , то график функции y = kx + b получается из y = kx со сдвигом на b единиц вверх вдоль оси OY
• если b

Есть два частных случая линейной функции

Если b = 0 , то уравнение примет вид « y = kx ». Такая функция называется прямой пропорциональностью . График — пряма я, которая проходит через начало координат .

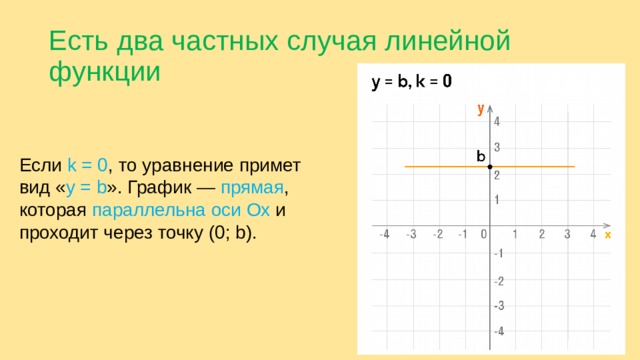
Есть два частных случая линейной функции

Если k = 0 , то уравнение примет вид « y = b ». График — прямая , которая параллельна оси Ох и проходит через точку (0; b).

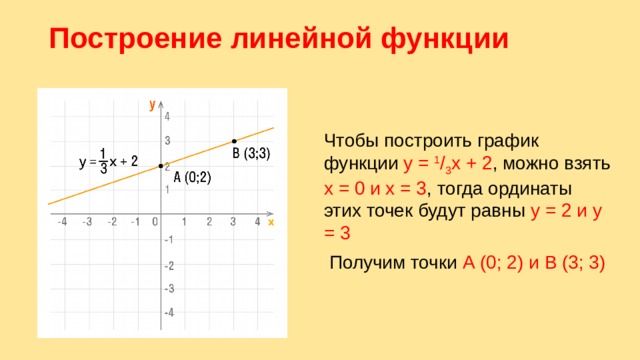
Построение линейной функции

Чтобы построить график функции y =  1 / 3 x + 2 , можно взять х = 0 и х = 3 , тогда ординаты этих точек будут равны у = 2 и у = 3

Получим точки А (0; 2) и В (3; 3)

Построение линейной функции

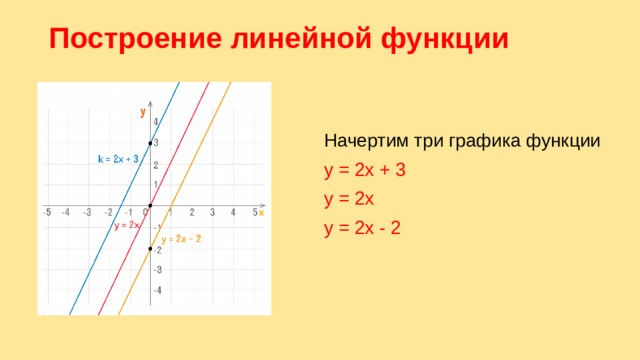
Начертим три графика функции

y = 2x + 3

y = 2x

y = 2x - 2

Ссылка на источник

• https://skysmart.ru