Векторы в пространстве
Выполнила
Ученица 11 класса «а»
МБУ ОО СОШ №1
Котова Мария
Руководитель Никитина Е.Г.
Понятие вектора
- Вектор – это отрезок, для которого указано, какой из его концов считается началом, а какой – концом.
- Направление вектора на рисунках отмечается стрелкой.
- Любая точка пространства также может рассматриваться как вектор. Такой вектор называется нулевым.
а
- Два ненулевых вектора называются коллинеарными , если они лежат на одной прямой или на параллельных прямых.
- Если два ненулевых вектора коллинеарны и если при этом их лучи соноправлены, то векторы сонаправлены , а если эти лучи не являются соноправленными, то векторы называются противоположно направленными .
АВ
CD
Векторы АВ и CD сонаправлены ( AB CD)
AB
Векторы АВ и CD противоположно направлены (AB CD)
CD
Равенство векторов
- Векторы называются равными , если они сонаправлены и их длины равны.
На рисунке AE=DK, так как
AE DK и AE = DK , а AB DC,
так как AB DC
От любой точки можно отложить
вектор, равный данному и притом
только один.
N
K
E
C
D
M
A
B
Сложение векторов
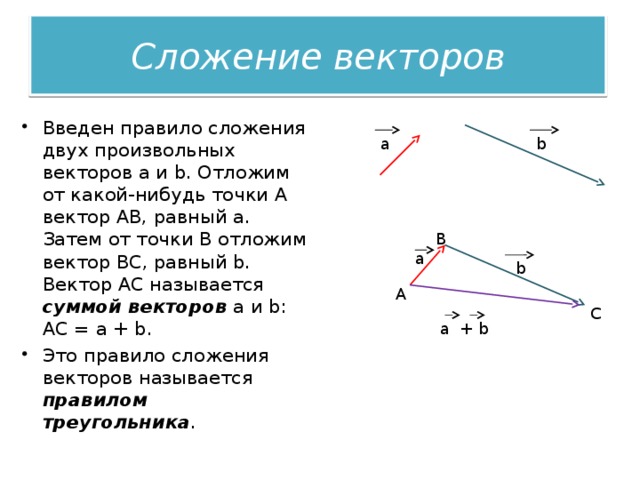
- Введен правило сложения двух произвольных векторов a и b. Отложим от какой-нибудь точки А вектор АВ, равный а. Затем от точки В отложим вектор ВС, равный b. Вектор АС называется суммой векторов a и b: АС = a + b.
- Это правило сложения векторов называется правилом треугольника .
а
b
B
а
b
A
C
a + b
a + b
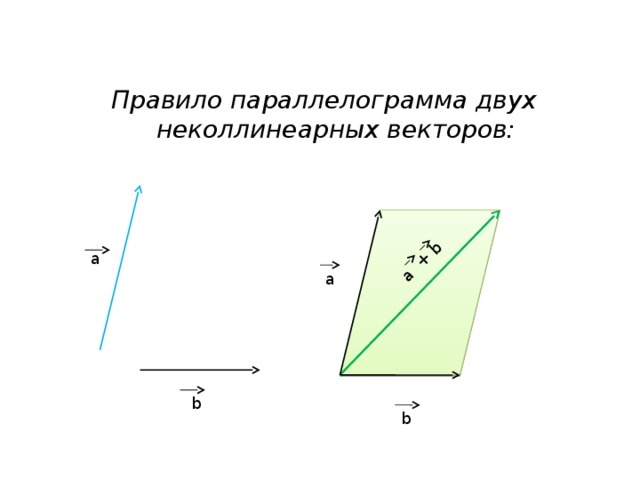
Правило параллелограмма двух неколлинеарных векторов:
а
а
b
b
Вычитание векторов
- Разностью векторов а и b называется такой вектор, сумма которого с вектором b равна вектору а . Разность векторов можно найти по формуле:
а – b = a + ( -b )
b
а
-b
a - b
а
Сумма нескольких векторов
Сложение нескольких векторов в пространстве выполняется так же, как и на плоскости: первый вектор складывается со вторым, затем их сумма – с третьим вектором и т.д. Из законов сложения векторов следует, что сумма нескольких векторов не зависит от того, в каком порядке они складываются.
а
b
a + b + c
с
с
а
b
0. Произведением нулевого вектора на любое число считается нулевой вектор. а Для любых векторов а, b и любых чисел k, l справедливы равенства: (kl) a = k (la) (сочетательный закон) k (a + b) = ka + kb (первый распределительный закон) (k + l) a = ka + la (второй распределительный закон) 2а " width="640"
Умножение вектора на число
Произведением ненулевого вектора а на число k называется такой вектор b, длина которого равна k * a , причем векторы а и b сонаправлены при k0.
Произведением нулевого вектора на любое число считается нулевой вектор.
а
Для любых векторов а, b и любых чисел k, l справедливы равенства:
- (kl) a = k (la) (сочетательный закон)
- k (a + b) = ka + kb (первый распределительный закон)
- (k + l) a = ka + la (второй распределительный закон)
2а
Компланарные векторы
- Векторы называются компланарными , если при откладывании их от одной и той же точки они будут лежать в одной плоскости.
- Если вектор с можно разложить по векторам а и b, т.е. представить в виде:
с = xa + yb ,
где x и y – некоторые числа, то векторы а, b и с компланарны.
Правило параллелепипеда
- Для сложения трех некомпланарных векторов можно пользоваться правилом параллелепипеда .
- Пусть а, b, с – некомпланарные векторы. Отложим от произвольной точки О пространства векторы ОА = а, ОВ = b, ОС = с и построим параллелепипед так, чтобы отрезки ОА, ОВ, ОС были его ребрами. Тогда диагональ OD этого параллелепипеда изображает сумму векторов а, b, c: OD = а + b + c. Действительно, OD = OE + ED = (OA + AE) + ED = OA + OB + OC = a + b + c.
D
G
C
F
c
Е
В
b
А
О
а
Разложение вектора по трем некомпланарным векторам
- Если вектор р представлен в виде:
p = xa + yb + zc,
Где x, y, z – некоторые число, то говорят, что вектор р разложен по векторам а, b и с . Числа x, y, z называются коэффициентами разложения .
Теорема:
Любой вектор можно разложить по трем некомпланарным векторам, причем коэффициенты разложения определяются единственным образом.
Получите свидетельство
Вход
Презентация по математике "Векторы в пространстве" (81.41 КB)
0
1848
169
Нравится
0
