Презентация по математике "Тетраэдр и параллелепипед. Построение сечений"

Какую тему изучали на прошлом уроке?

Тетраэдр и параллелепипед.

Как называется раздел геометрии, в котором изучают многогранники? (Стереометрия)

Какие многогранники вы знаете?

- Куб, цилиндр, шар, конус, пирамида, параллелепипед.

Что называется тетраэдром?

Поверхность, составленная из четырех треугольников называется тетраэдром.

Что называется параллелепипедом?

Параллелепипедом называется фигура, которая состоит из шести параллелограммов.

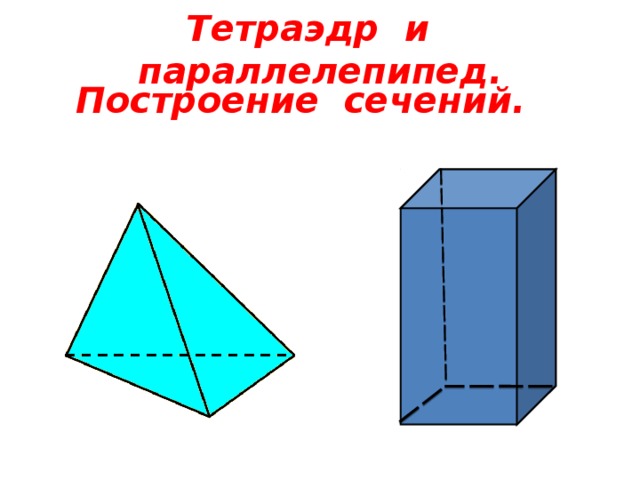
Тетраэдр и параллелепипед.

Построение сечений.

Какую тему изучали на прошлом уроке?

Тетраэдр и параллелепипед.

Как называется раздел геометрии, в котором изучают многогранники?

Стереометрия

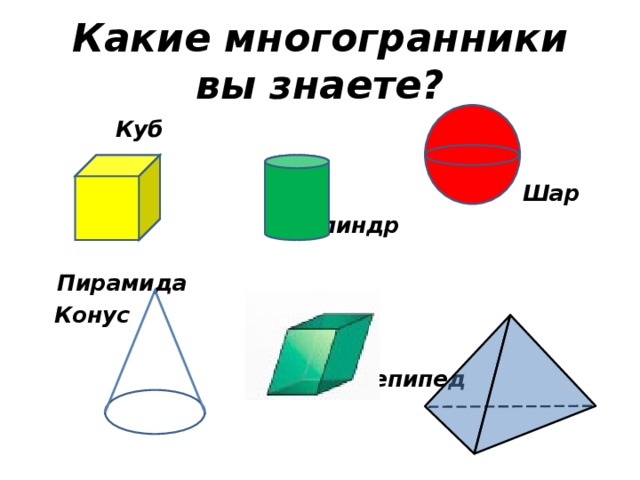
Какие многогранники вы знаете?

Куб

Шар

Цилиндр

Пирамида

Конус

Параллелепипед

Сегодня поговорим о многогранниках:

тетраэдре и параллелепипеде.

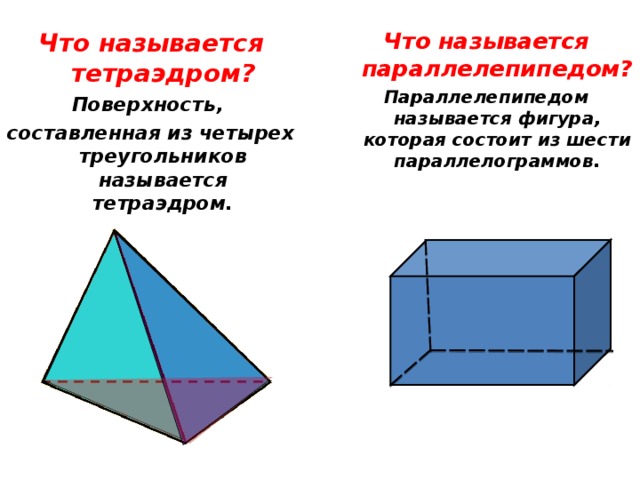
Что называется тетраэдром?

Что называется параллелепипедом?

Параллелепипедом называется фигура, которая состоит из шести параллелограммов.

Поверхность,

составленная из четырех треугольников называется тетраэдром.

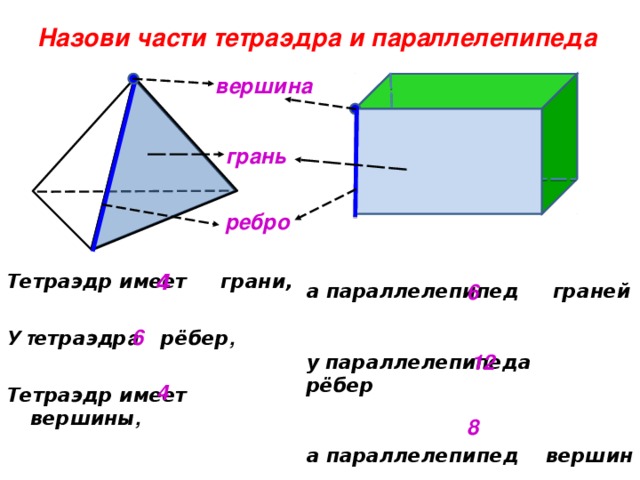
Назови части тетраэдра и параллелепипеда

вершина

грань

ребро

4

Тетраэдр имеет грани,

У т етраэдр а рёбер ,

Тетраэдр имеет вершины ,

6

а параллелепипед граней

у параллелепипеда рёбер

а параллелепипед вершин

6

12

4

8

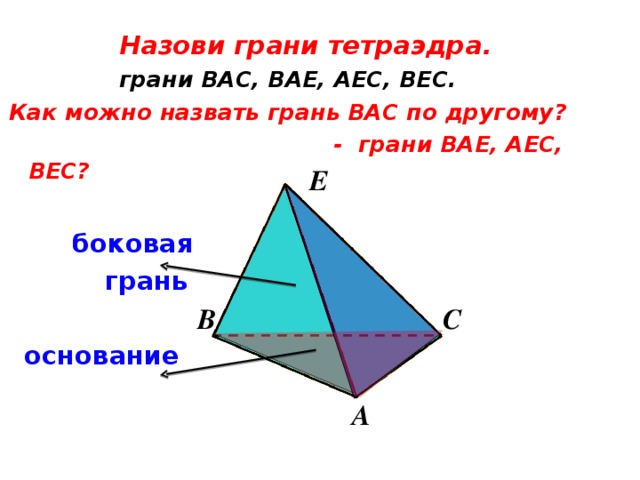
Назови грани тетраэдра.

грани ВАС, ВАЕ, АЕС, ВЕС.

Как можно назвать грань ВАС по другому?

- грани ВАЕ, АЕС, ВЕС?

боковая

грань

основание

Е

B

С

А

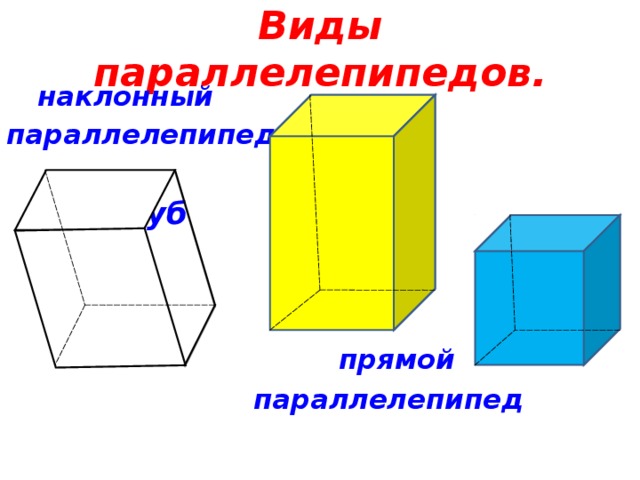
Виды параллелепипедов.

наклонный

параллелепипед

Куб

прямой

параллелепипед

Свойства параллелепипеда:

1. Противоположные грани параллелепипеда

параллельны и равны.

2. Диагонали параллелепипеда

пересекаются в одной точке

и делятся этой точкой пополам.

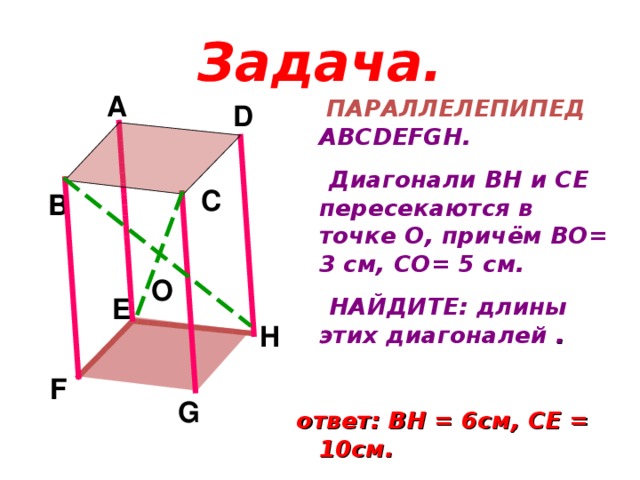
Задача.

A

ПАРАЛЛЕЛЕПИПЕД ABCDEFGH .

Диагонали В H и CE пересекаются в точке О, причём ВО= 3 см, СО= 5 см.

НАЙДИТЕ: длины этих диагоналей .

ответ: ВН = 6см, СЕ = 10см.

D

C

B

О

E

H

F

G

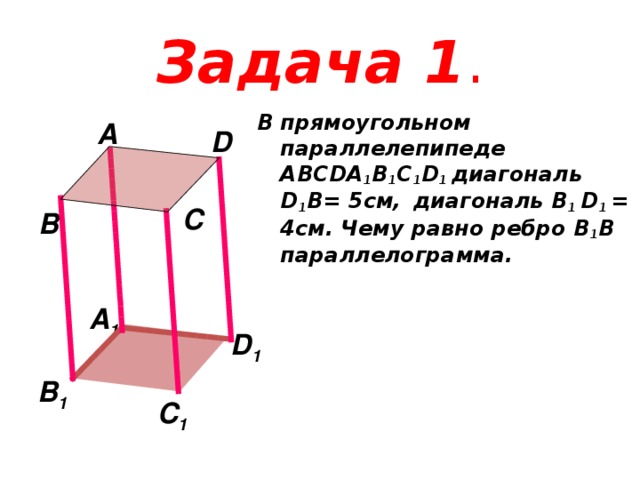
Задача 1 .

В прямоугольном параллелепипеде ABCDA 1 B 1 C 1 D 1 диагональ D 1 В= 5см, диагональ B 1 D 1 = 4см. Чему равно ребро B 1 B параллелограмма.

A

D

C

B

A 1

D 1

B 1

C 1

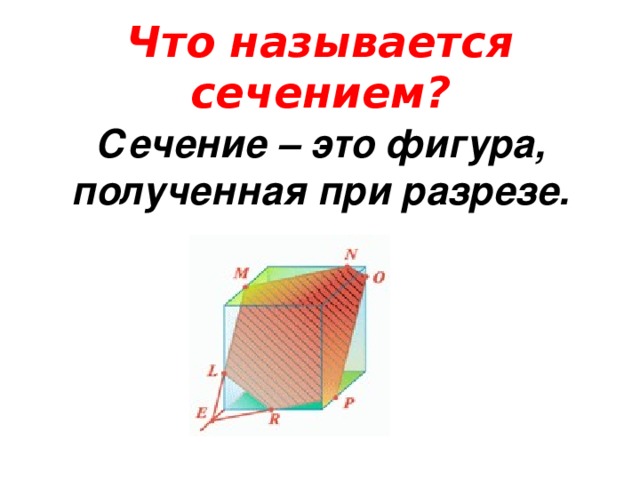
Что называется сечением?

Сечение – это фигура, полученная при разрезе.

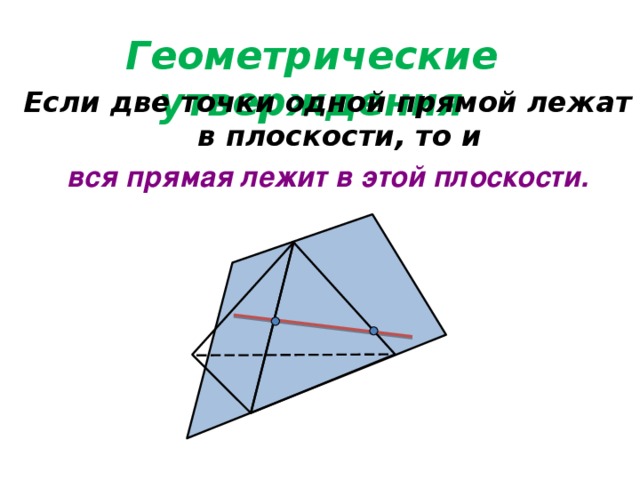
Геометрические утверждения

Если две точки одной прямой лежат в плоскости, то и

вся прямая лежит в этой плоскости.

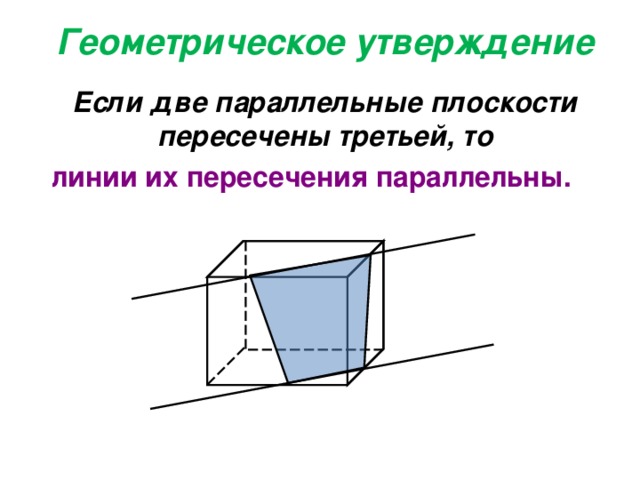
Геометрическое утверждение

Если две параллельные плоскости пересечены третьей, то

линии их пересечения параллельны.

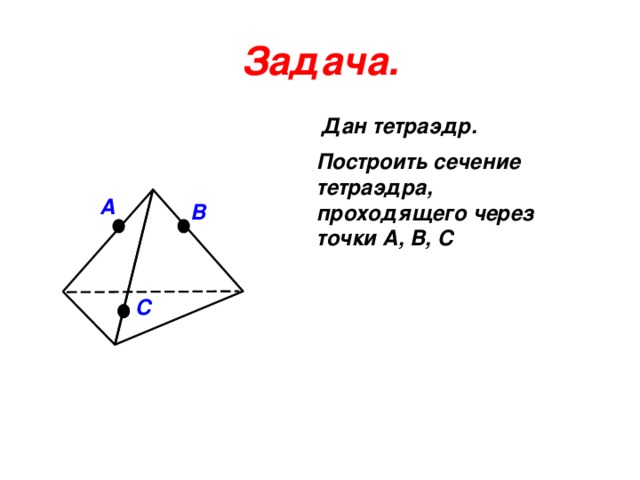
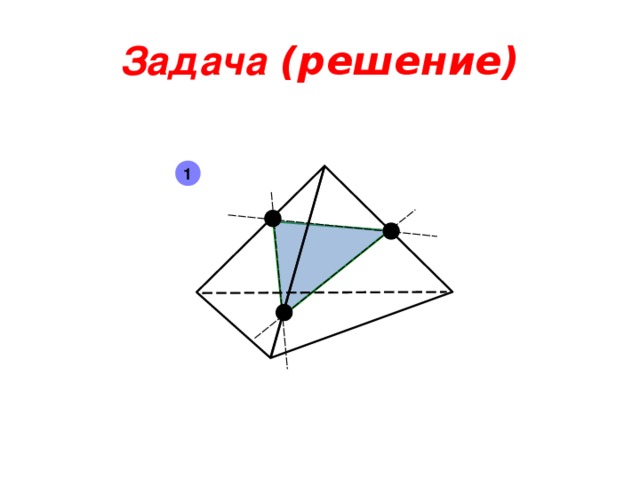
Задача.

Дан тетраэдр.

Построить сечение

тетраэдра,

проходящего через

точки A, B, C

A

B

C

Задача ( решение)

1

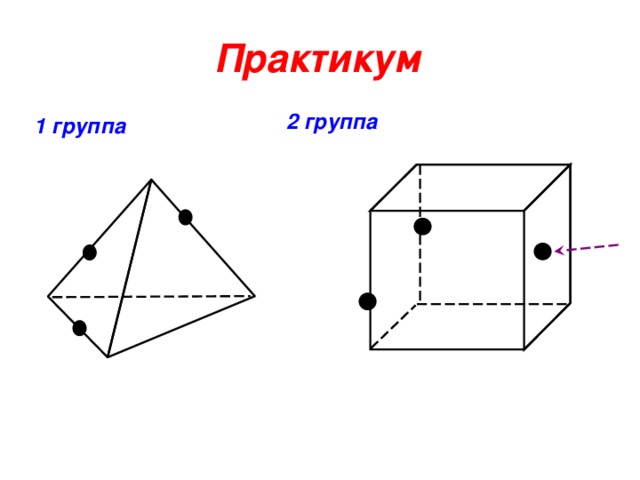
Практикум

2 группа

1 группа

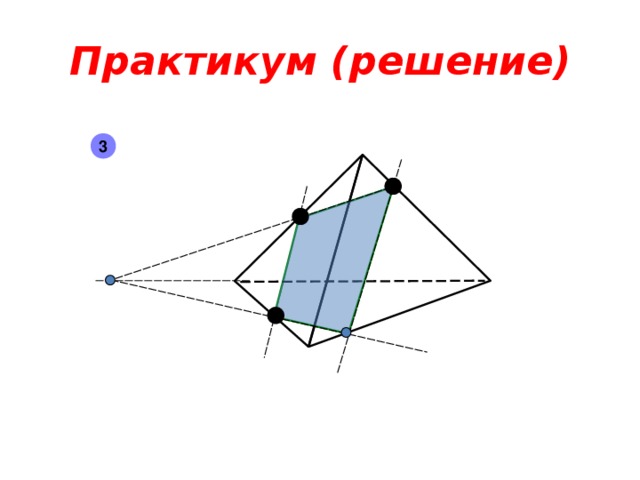
Практикум ( решение)

3

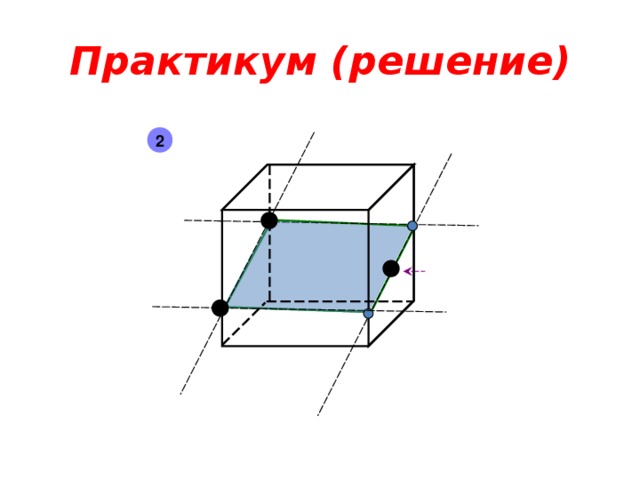
Практикум ( решение)

2

Домашнее задание.

• Повторить по тетради.
• Построить тетраэдр EDFK

Записать все его ребра, грани и вершины.

• Построить сечение фигуры.

Итог урока.

• Чем сегодня занимались на уроке?
• Вам урок понравился?