Математик так же, как художник или поэт, создает узоры. И если его узоры более устойчивы, то лишь потому, что они созданы из идей...
Г.Х. Харди
Подготовила: учитель математики Кужелева О. А.
При решении широкого класса задач с параметром довольно часто оказывается полезным графический метод.
Решение задач с параметром графическим методом имеет ряд особенностей. Он основан на нахождении всех точек данной плоскости, координаты которых удовлетворяют заданному в условии задачи соотношению.
Графический метод обладает целым рядом преимуществ перед аналитическим: он более нагляден и понятен в случаях, когда необходимо ответить на качественный вопрос или провести анализ множества решений. Однако следует помнить, что универсальных методов и приёмов, пригодных для любой математической задачи, не существует. Поэтому, приступая к анализу той или иной задачи, необходимо выбрать наиболее эффективный из возможных способов её решения.
Цель:
- показать применение графического метода при решении задач с параметром;
- показать наглядность использования ИКТ при решении задач с помощью «живых графиков»;
- рассмотреть решение заданий С5 для подготовки к ЕГЭ.
Движение прямой вдоль оси Оу и число решений системы.
Справочный материал
у= k х+ b – линейная функция, Г – прямая
k – угловой коэффициент, k = tg α
b – точка пересечения Г с Оу
Если х = 0, то у = b , прямая параллельная Ох
{
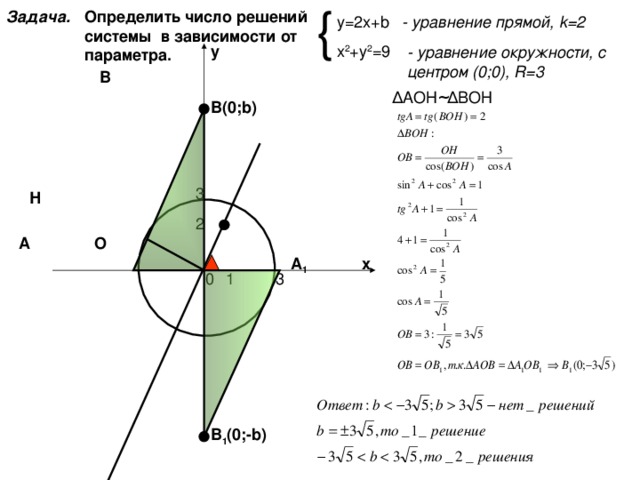
Определить число решений системы в зависимости от параметра.
Задача.
у=2х+ b
х 2 +у 2 =9
- уравнение прямой, k =2
у
- уравнение окружности, с центром (0;0), R=3
В
Δ АОН ~ Δ ВОН
В(0; b )
Н
А
О
А 1
х
В 1 (0;- b )
0, следовательно k 0; Если угол тупой, тогда tg α 0, следовательно k ; Если α = 90 º , то tg90º - не существует, следовательно не существует k. " width="640"
Угловой коэффициент прямой и число решений системы.
Справочный материал
у= k х+ b – линейная функция, Г – прямая
k – угловой коэффициент, k = tg α
Если угол острый, тогда tg α 0, следовательно k 0;
Если угол тупой, тогда tg α 0, следовательно k ;
Если α = 90 º , то tg90º - не существует, следовательно не существует k.
{
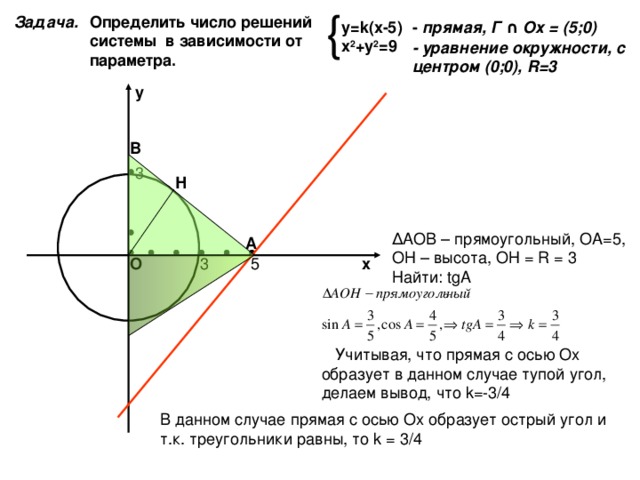
Определить число решений системы в зависимости от параметра.
Задача.
у= k( х -5)
х 2 +у 2 =9
- прямая, Г ∩ Ох = (5;0)
- уравнение окружности, с центром (0;0), R=3
у
В
Н
Δ АОВ – прямоугольный, ОА=5, ОН – высота, ОН = R = 3 Найти: tgA
А
х
О
Учитывая, что прямая с осью Ох образует в данном случае тупой угол, делаем вывод, что k=-3/4
В данном случае прямая с осью Ох образует острый угол и т.к. треугольники равны, то k = 3/4
{
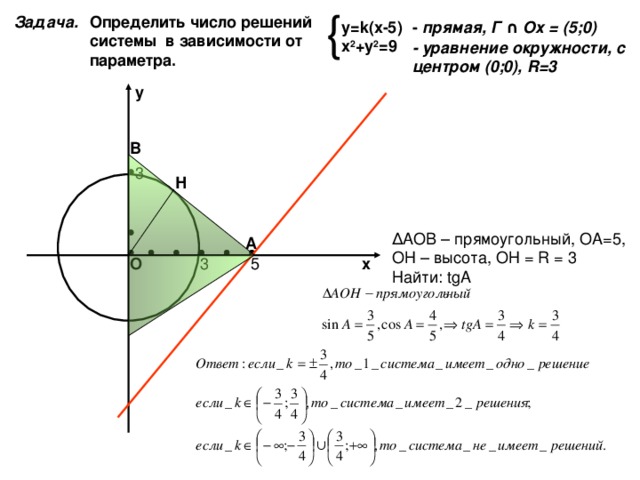
Задача.
Определить число решений системы в зависимости от параметра.
- прямая, Г ∩ Ох = (5;0)
у= k( х -5)
х 2 +у 2 =9
- уравнение окружности, с центром (0;0), R=3
у
В
Н
Δ АОВ – прямоугольный, ОА=5, ОН – высота, ОН = R = 3 Найти: tgA
А
О
х
Плавающая окружность и число решений системы.
Справочный материал.
(х – х 0 ) 2 + (у –у 0 ) 2 = R 2
(х 0 ;у 0 ) – координаты центра окружности
(х;у) – координаты точки, принадлежащей окружности
R – радиус окружности
{
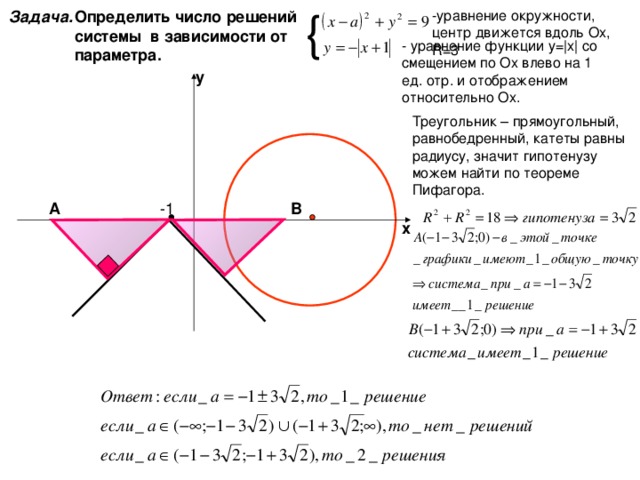
-уравнение окружности, центр движется вдоль Ох, R=3
Определить число решений системы в зависимости от параметра.
Задача.
- уравнение функции у= | х | со смещением по Ох влево на 1 ед. отр. и отображением относительно Ох.
у
Треугольник – прямоугольный, равнобедренный, катеты равны радиусу, значит гипотенузу можем найти по теореме Пифагора.
А
В
х
Движение параболы вдоль Оу и число решений системы
Справочный материал.
у = ах 2 + b х+с,
С помощью выделения полного квадрата получим у= k (х-х 0 ) 2 +у 0 , где (х 0 ;у 0 ) -координаты вершины параболы
-1 -0,5х 2 + b =-3х+3; у х 2 -6х+6-2 b=0 ; D=0 ; b = -1,5 2 решения будем иметь до момента касания параболы со вторым лучом «галочки» 3 решения получим при касании параболы и луча у=3х+9, при х -1 -0,5х 2 + b=3x+9 x 2 +6x+18-2b=0 D=0 ; b = 4,5 х 4 решения до момента прохождения параболы через точку (-1;6) В момент прохождения параболы через точку (-1;6) имеем: -0,5(-1)2+ b=6; b = 6,5 (3 реш.) При дальнейшем увеличении b графики будут иметь 2 общие точки, соответственно система – 2 решения " width="640"
{
Задача.
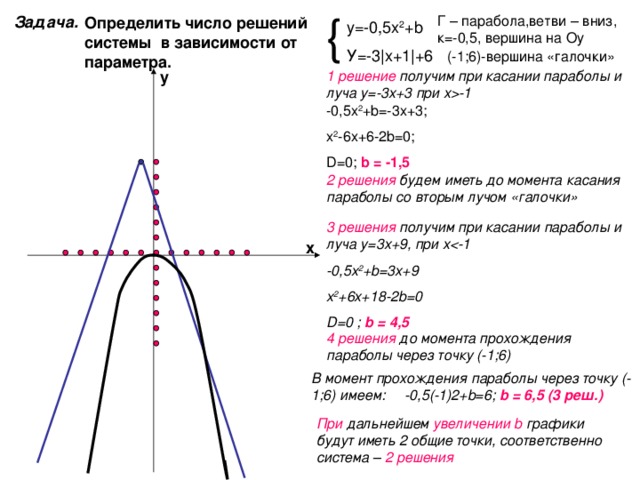
Г – парабола,ветви – вниз, к=-0,5, вершина на Оу
Определить число решений системы в зависимости от параметра.
у=-0,5х 2 + b
У=-3 | х+1 | +6
(-1;6)-вершина «галочки»
1 решение получим при касании параболы и луча у=-3х+3 при х -1 -0,5х 2 + b =-3х+3;
у
х 2 -6х+6-2 b=0 ;
D=0 ; b = -1,5
2 решения будем иметь до момента касания параболы со вторым лучом «галочки»
3 решения получим при касании параболы и луча у=3х+9, при х -1
-0,5х 2 + b=3x+9
x 2 +6x+18-2b=0
D=0 ; b = 4,5
х
4 решения до момента прохождения параболы через точку (-1;6)
В момент прохождения параболы через точку (-1;6) имеем: -0,5(-1)2+ b=6; b = 6,5 (3 реш.)
При дальнейшем увеличении b графики будут иметь 2 общие точки, соответственно система – 2 решения
График модуля меняет угловой коэффициент и число решений системы.
Справочный материал.
у = k | х-а | + b
(a;b) – координаты вершины «галочки»
k – угловой коэффициент лучей «галочки»
0 ; одно решение Два решения , если луч «галочки» проходит через точку (0;-2), т.е. р | 0+2 | -3=-2; р=0,5 Одно решение х " width="640"
{
Задача.
Определить число решений системы в зависимости от параметра.
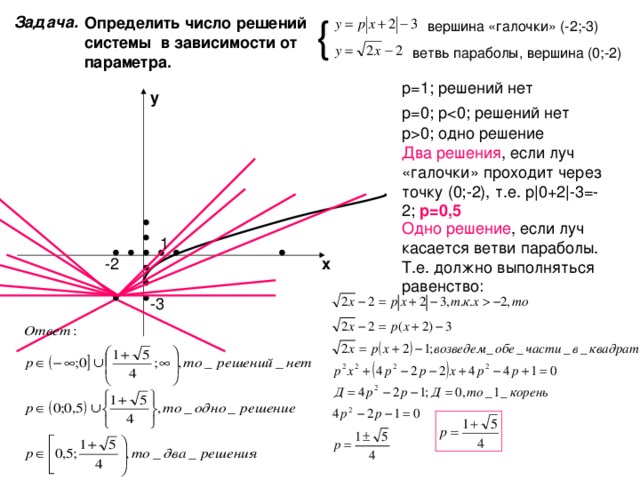
вершина «галочки» (-2;-3)
ветвь параболы, вершина (0;-2)
у
р=0; р
р 0 ; одно решение
Два решения , если луч «галочки» проходит через точку (0;-2), т.е. р | 0+2 | -3=-2; р=0,5
Одно решение
х
Окружность с фиксированным центром меняет радиус и число решений системы.
Справочный материал.
(х-а) 2 +(у- b) 2 =R 2
(a,b) -координаты центра
R - радиус
x 2 +y 2 =c 2 – уравнение окружности с центром в начале координат
(0;0) – координаты центра
R= |c| , с – принимает как положительные, так и отрицательные значения.
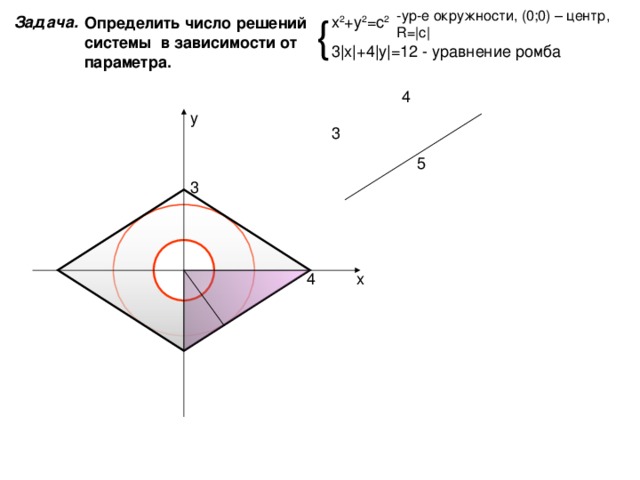
- ур-е окружности, (0;0) – центр, R= |c|
{
х 2 +у 2 =с 2
3 | х | +4 | у | =12
Задача.
Определить число решений системы в зависимости от параметра.
4
y
3
5
3
x
4
0 { Ур-е окружности, (5 ; 4)- центр, R=3 2 2 2 2 2 Ур-е окр.,(-2;0)-центр, R= |a| D Δ АВС-прямоугольный, АС=4; ВС=7. А М х 2 случай. х { Н В Ур-е окружности, (-5 ; 4)- центр, R=3 С (х + 5) 2 +(у-4) 2 =9 (х+2) 2 +у 2 =а 2 Δ МНВ - прямоугольный, МН=4;НВ=3; след. МВ=5 Найди ошибку! " width="640"
{
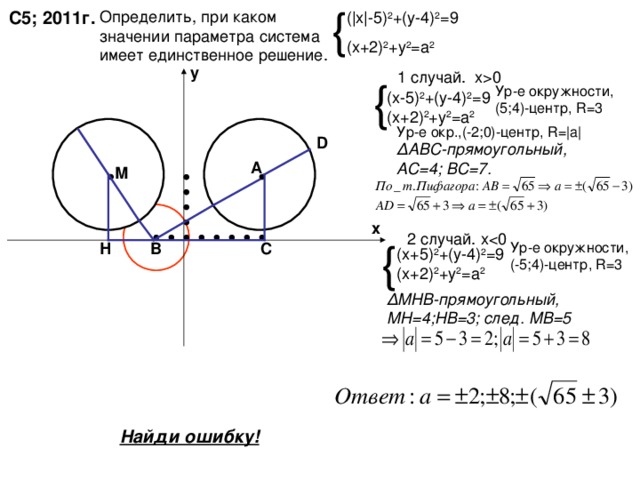
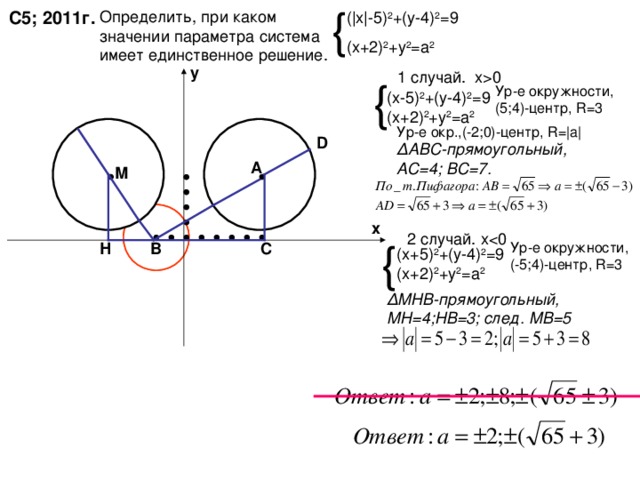
С5; 2011г.
( | х | -5) 2 +(у-4) 2 =9
(х+2) 2 +у 2 =а 2
у
1 случай. х 0
{
Ур-е окружности, (5 ; 4)- центр, R=3
2 2
2 2 2
Ур-е окр.,(-2;0)-центр, R= |a|
D
Δ АВС-прямоугольный, АС=4; ВС=7.
А
М
х
2 случай. х
{
Н
В
Ур-е окружности, (-5 ; 4)- центр, R=3
С
(х + 5) 2 +(у-4) 2 =9
(х+2) 2 +у 2 =а 2
Δ МНВ - прямоугольный, МН=4;НВ=3; след. МВ=5
Найди ошибку!
0 { Ур-е окружности, (5 ; 4)- центр, R=3 2 2 2 2 2 Ур-е окр.,(-2;0)-центр, R= |a| D Δ АВС-прямоугольный, АС=4; ВС=7. А М х 2 случай. х { Н С В Ур-е окружности, (-5 ; 4)- центр, R=3 (х + 5) 2 +(у-4) 2 =9 (х+2) 2 +у 2 =а 2 Δ МНВ - прямоугольный, МН=4;НВ=3; след. МВ=5 " width="640"
{
С5; 2011г.
( | х | -5) 2 +(у-4) 2 =9
(х+2) 2 +у 2 =а 2
у
1 случай. х 0
{
Ур-е окружности, (5 ; 4)- центр, R=3
2 2
2 2 2
Ур-е окр.,(-2;0)-центр, R= |a|
D
Δ АВС-прямоугольный, АС=4; ВС=7.
А
М
х
2 случай. х
{
Н
С
В
Ур-е окружности, (-5 ; 4)- центр, R=3
(х + 5) 2 +(у-4) 2 =9
(х+2) 2 +у 2 =а 2
Δ МНВ - прямоугольный, МН=4;НВ=3; след. МВ=5
1 2ax + |x 2 -8x + 7 | 1 |x 2 -8x + 7 | -2ax + 1 у Рассмотрим обе части неравенства как функции и построим их графики. 1) у = |x 2 -8x + 7 | - график – парабола, часть параболы для у х а = 0,5 2 2 1 2 2 2 1 2 " width="640"
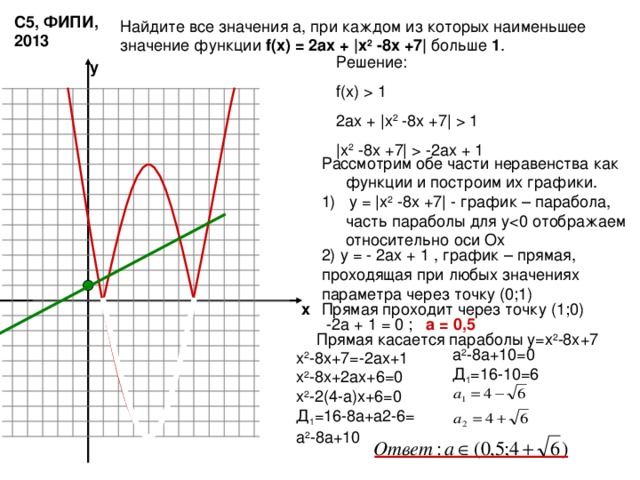
С5, ФИПИ, 2013
Найдите все значения а, при каждом из которых наименьшее значение функции f(x) = 2ax + |x 2 -8x + 7 | больше 1 .
Решение:
f(x) 1
2ax + |x 2 -8x + 7 | 1
|x 2 -8x + 7 | -2ax + 1
у
Рассмотрим обе части неравенства как функции и построим их графики.
1) у = |x 2 -8x + 7 | - график – парабола, часть параболы для у
х
а = 0,5
2
2 1
2 2 2 1 2
Вариант 1
Найдите все положительные значения параметра а, при которых система имеет единственное решение
Вариант 2
Найдите все значения параметра а, при каждом из которых система имеет ровно три различных решения
Вариант 3
Найдите все значения а, при каждом из которых наименьшее значение функции f (х) = 2ах + | х 2 – 8х + 15 | больше 1.
Ответы:
Получите свидетельство
Вход
Презентация по математике "Решение задач с параметром" (0.42 MB)
0
858
111
Нравится
0
