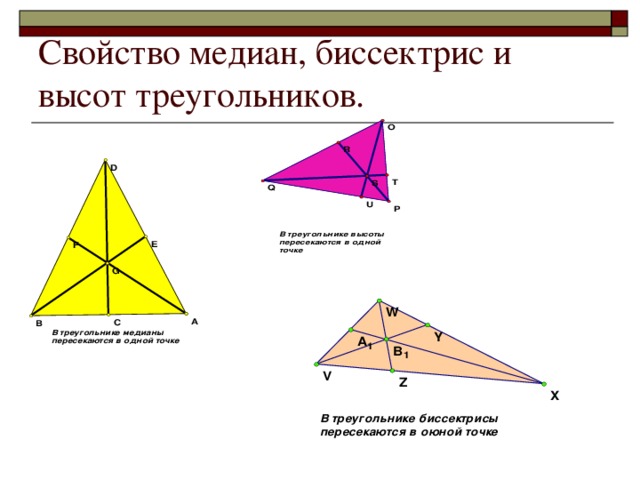
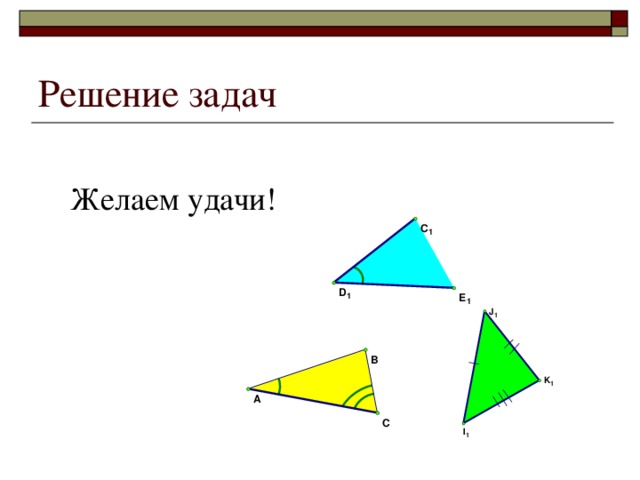
В начале урока вспомним, что такое треугольник, исторические сведения о нем. Рассмотрим виды треугольников. Также познакомимся с высотой, медианой и биссектрисой треуголиника, их свойствами. Затем рассмотрим три вида равенства треугольника и для закрепления материала, приступим к решению задач.

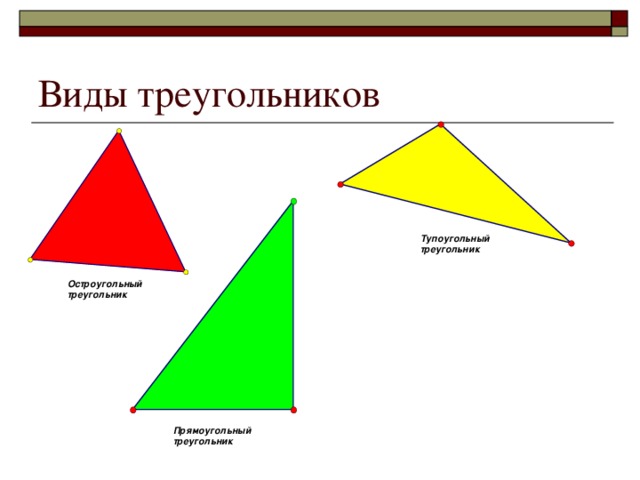
Треугольник - простейшая плоская фигура. Три вершины и три стороны. Изучение треугольника породило науку – тригонометрию. Эта наука возникла из практических потребностей при измерении земельных участков, составлении карт на местности, конструировании машин и механизмов.
Первое упоминание о треугольнике и его свойствах мы находим в египетских папирусах
Открытия в геометрии треугольника есть и в нашем веке
Так, в 1904 году американский математик Ф.Морли доказал , что если из каждой вершины треугольника провести лучи, делящие соответствующий угол на три равные части(трисектрисы угла,) то точки пересечения смежных трисектрис углов являются вершинами равностороннего треугольника. Доказательство этого утверждения было под силу и древнегреческим математикам , но они прошли мимо этого факта, видимо, потому, что тогда было принято рассматривать лишь построения при помощи циркуля и линейки, а с помощью этих инструментов такое деление сделать не возможно.

 Получите свидетельство
Получите свидетельство Вход
Вход








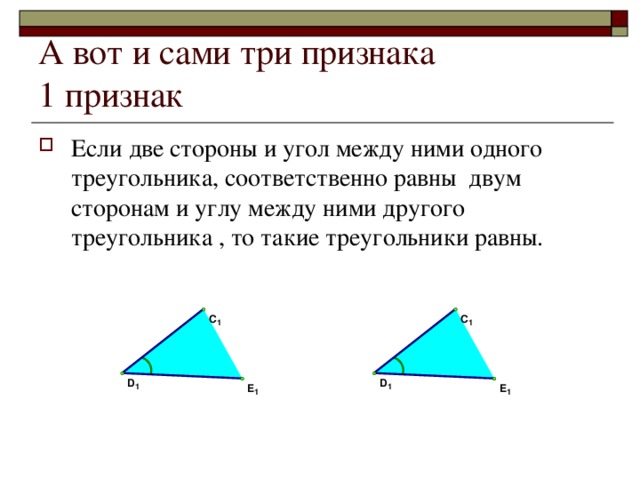











 Презентация по математике "Признаки равенства треугольников" (0.22 MB)
Презентация по математике "Признаки равенства треугольников" (0.22 MB)
 0
0 421
421 57
57 Нравится
0
Нравится
0


