
Подготовка к ЕГЭ по математике Теория и практика. Задание В9.

Для решения данной группы задач необходимо знать:
- таблицу производных и правила дифференцирования
- геометрический смысл производной
- свойства производной для исследования функций
- физический (механический) смысл производной
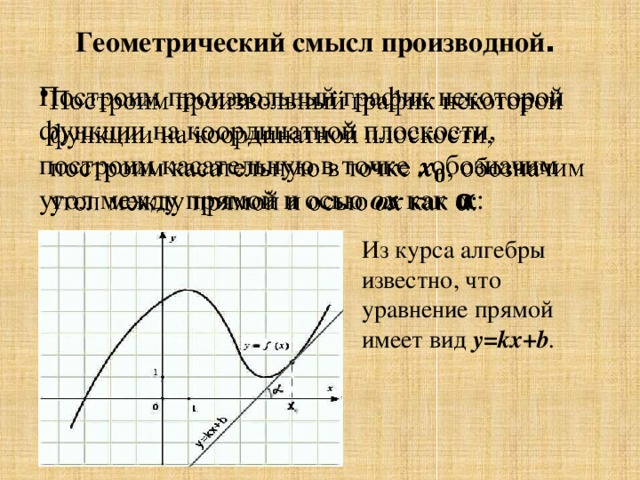
Геометрический смысл производной .
Построим произвольный график некоторой функции на координатной плоскости, построим касательную в точке , обозначим угол между прямой и осью ox как α :
Из курса алгебры известно, что уравнение прямой имеет вид y=kx+b .

Геометрический смысл производной .
Производная функции в точке есть угловой коэффициент касательной к графику этой функции в этой точке.
В этом и состоит геометрический смысл производной. То есть производная функции в точке равна угловому коэффициенту k касательной :′(x)=k . А угловой коэффициент в свою очередь равен тангенсу угла α, то есть: ′(x)=k =tg α.

Геометрический смысл производной .
По свойству тангенса:
при 0 имеет положительное значение (значит производная имеет положительное значение)
при α=0 tgα равен нулю (значит производная равна нулю)
при 90 tgα имеет отрицательное значение (значит производная имеет отрицательное значение)

Задания на применение геометрического смысла производной
- Прямая y=7x-5 параллельна касательной к графику функции y= . Найдите абсциссу точки касания.
- Прямая y=-4x-11 является касательной к графику функции . Найдите абсциссу точки касания.
- Прямая y= 3x+4 является касательной к графику функции = . Найдите c .
- Прямая y=3x+1 является касательной к графику функции y= . Найдите a .
- Прямая y=-5x+8 является касательной к графику функции y=28x+15 . Найдите b , учитывая, что абсцисса точки касания больше 0.

Физический (механический) смысл производной.
Пусть задан закон движения материальной точки x(t) вдоль координатной оси, где x координата движущейся точки, t – время. Скорость в определённый момент времени – это производная координаты по времени . В этом и состоит механический смысл производной .
V(t)=x‘(t)

Физический (механический) смысл производной.
Таким образом, физический смысл производной это скорость. Это может быть скорость движения, скорость изменения какого либо процесса (например роста бактерий), скорость совершения работы (и так далее, прикладных задач множество).

Задания на применение физического смысла производной.
- Материальная точка движется прямолинейно по закону x(t)= (где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). В какой момент времени (в секундах) ее скорость была равна 2 м/с?
- Материальная точка движется прямолинейно по закону x(t)= - (где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). Найдите ее скорость (в м/с) в момент времени с.

Свойства производной для исследования функций
Если значение производной в определённой точке из некоторого интервала имеет положительное значение( 0 ), то график функции на этом интервале возрастает.
Если значение производной в определённой точке из некоторого интервала имеет отрицательное значение ( 90 ) , то график функции на этом интервале убывает.
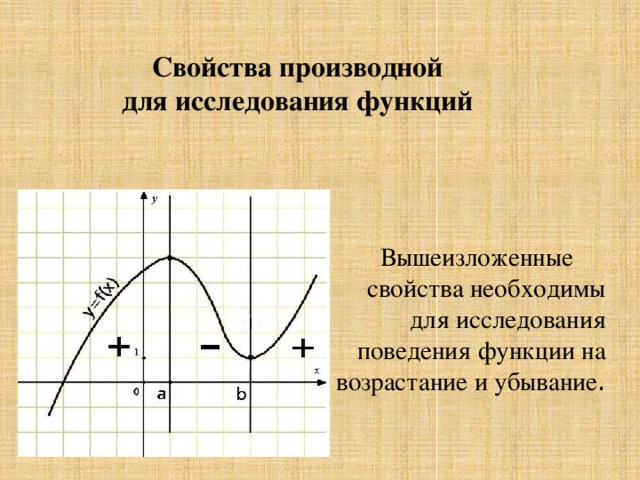
Свойства производной для исследования функций
Вышеизложенные свойства необходимы для исследования поведения функции на возрастание и убывание .

Свойства производной для исследования функций
Точки, в которых функция меняет своё поведение с возрастания на убывание (и наоборот, с убывания на возрастание), называются экстремумами. Их ещё называют точками максимума (минимума) функции. Производная в этих точках равна нулю. Касательные в этих точках параллельны оси ox.

Какие выводы мы можем сделать, когда дан график функции?
- Можем определить интервалы возрастания (убывания) функции, знак производной на этом интервале.
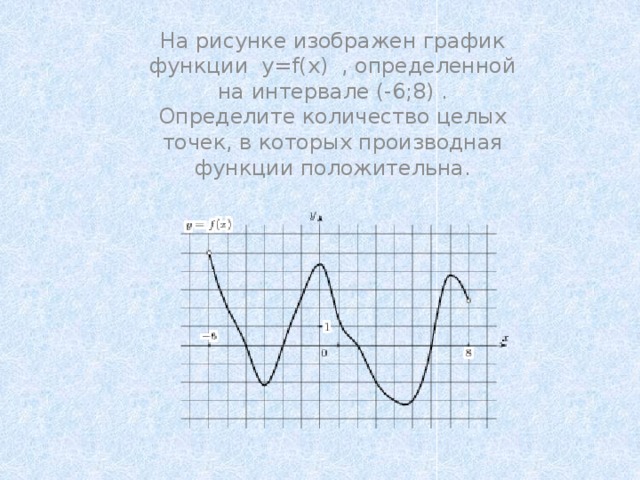
На рисунке изображен график функции y=f(x) , определенной на интервале (-6;8) . Определите количество целых точек, в которых производная функции положительна.
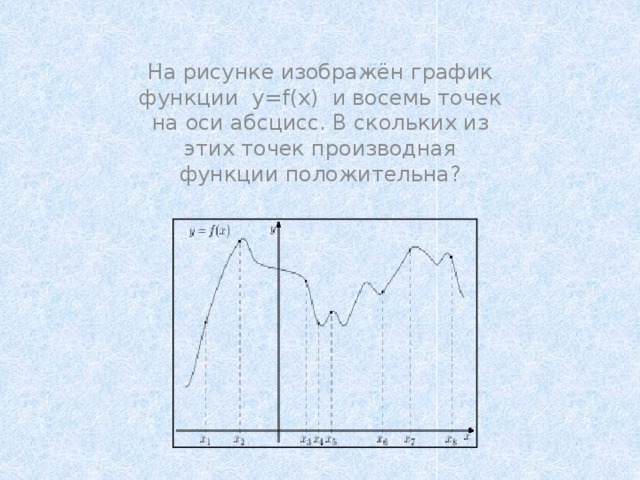
На рисунке изображён график функции y=f(x) и восемь точек на оси абсцисс. В скольких из этих точек производная функции положительна?

Какие выводы мы можем сделать, когда дан график функции?
2. Можем определить точки максимума (минимума) функции (если задан масштаб), их количество.
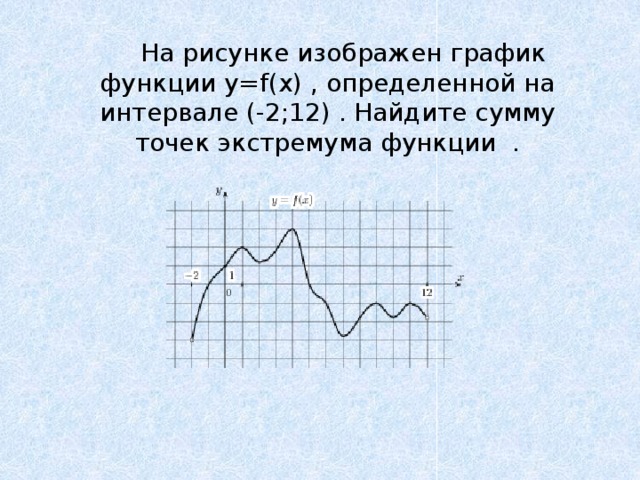
На рисунке изображен график функции y=f(x) , определенной на интервале (-2;12) . Найдите сумму точек экстремума функции .

Какие выводы мы можем сделать, когда дан график функции?
4.Можем определить количество точек, в которых производная равна нулю.
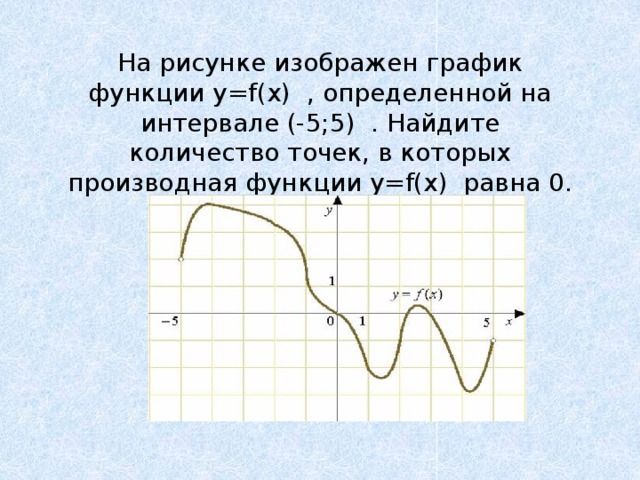
На рисунке изображен график функции y=f(x) , определенной на интервале (-5;5) . Найдите количество точек, в которых производная функции y=f(x) равна 0.

Какие выводы мы можем сделать, когда дан график функции?
5. Количество касательных к графику функции, параллельных оси ox .
6. Количество касательных, параллельных какой-либо данной прямой.
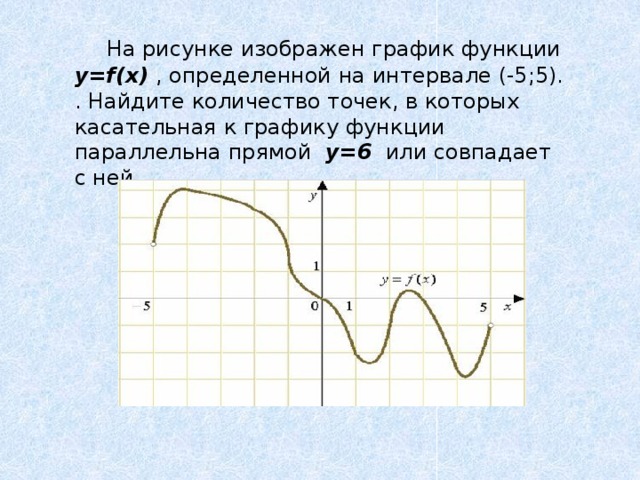
На рисунке изображен график функции y=f(x) , определенной на интервале (-5;5). . Найдите количество точек, в которых касательная к графику функции параллельна прямой y=6 или совпадает с ней.

Какие выводы мы можем сделать, когда дан график функции?
7. Значение производной функции в некоторой точке, если даны две точки, через которые проходит касательная.
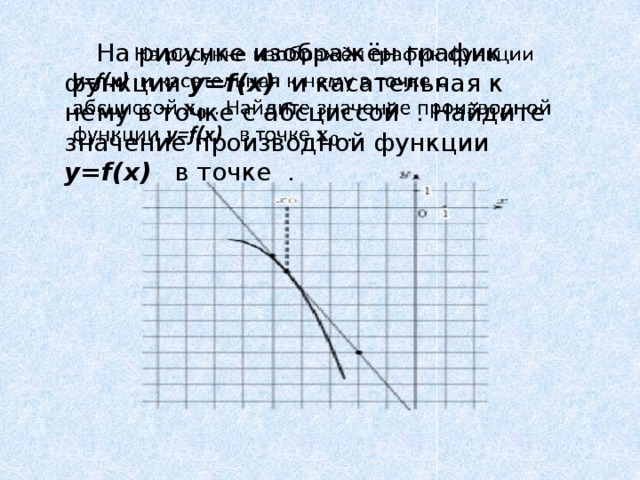
На рисунке изображён график функции y=f(x) и касательная к нему в точке с абсциссой . Найдите значение производной функции y=f(x) в точке .

Какие выводы мы можем сделать, когда дан график функции?
8. В какой из точек графика функции значение производной наименьшее (наибольшее).
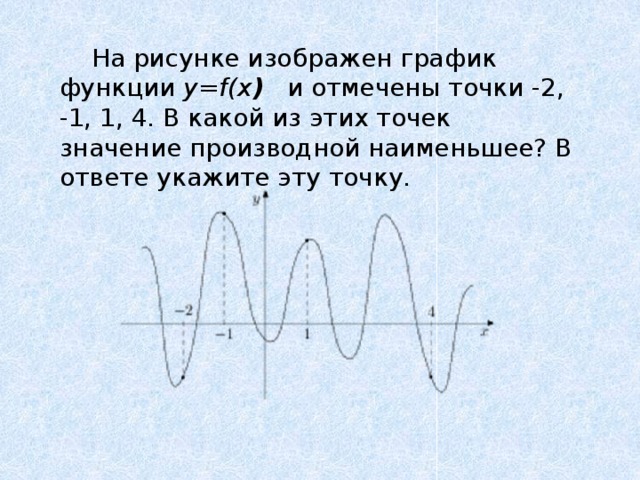
На рисунке изображен график функции y=f(x ) и отмечены точки -2, -1, 1, 4. В какой из этих точек значение производной наименьшее? В ответе укажите эту точку.
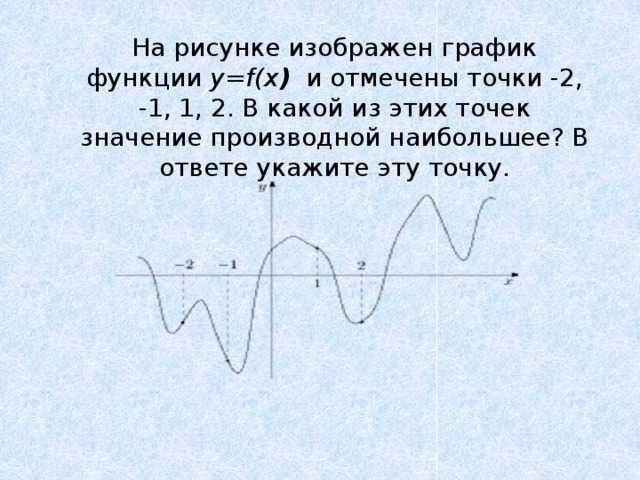
На рисунке изображен график функции y=f(x ) и отмечены точки -2, -1, 1, 2. В какой из этих точек значение производной наибольшее? В ответе укажите эту точку.

Какие выводы мы можем сделать, когда дан график производной функции?
1. Можем определить интервалы, на которых функция возрастает (убывает).
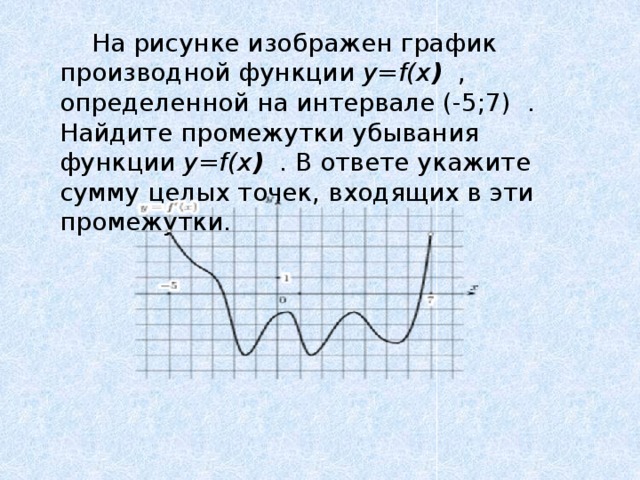
На рисунке изображен график производной функции y=f(x ) , определенной на интервале (-5;7) . Найдите промежутки убывания функции y=f(x ) . В ответе укажите сумму целых точек, входящих в эти промежутки.
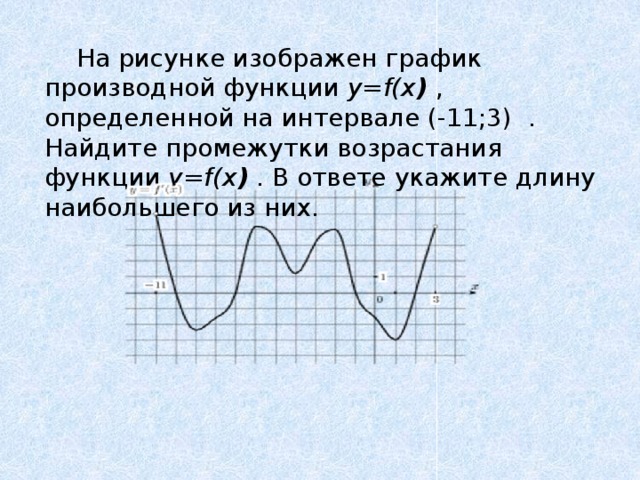
На рисунке изображен график производной функции y=f(x ) , определенной на интервале (-11;3) . Найдите промежутки возрастания функции y=f(x ) . В ответе укажите длину наибольшего из них.

Какие выводы мы можем сделать, когда дан график производной функции?
2. Точки минимума (максимума) функции.
3. Количество точек минимума (максимума) функции.
4. Количество экстремумов функции.
![На рисунке изображен график производной функции y=f(x ) , определенной на интервале (-4;8) . Найдите точку экстремума функции на отрезке [-2;6]](https://fsd.videouroki.net/html/2014/10/29/98690319/img30.jpg)
На рисунке изображен график производной функции y=f(x ) , определенной на интервале (-4;8) . Найдите точку экстремума функции на отрезке [-2;6]
![На рисунке изображен график производной функции y=f(x ) , определенной на интервале (-18;6) . Найдите количество точек минимума функции на отрезке [-13;1] .](https://fsd.videouroki.net/html/2014/10/29/98690319/img31.jpg)
На рисунке изображен график производной функции y=f(x ) , определенной на интервале (-18;6) . Найдите количество точек минимума функции на отрезке [-13;1] .
![На рисунке изображен график производной функции y=f(x ) , определенной на интервале (-11;11) . Найдите количество точек экстремума функции y=f(x ) на отрезке [-10;10] .](https://fsd.videouroki.net/html/2014/10/29/98690319/img32.jpg)
На рисунке изображен график производной функции y=f(x ) , определенной на интервале (-11;11) . Найдите количество точек экстремума функции y=f(x ) на отрезке [-10;10] .

Какие выводы мы можем сделать, когда дан график производной функции?
5. Можем определить точки, в которых функция приобретает максимальное (минимальное) значение на заданном интервале.
![На рисунке изображен график производной функции y=f(x ) , определенной на интервале (-8;4) . В какой точке отрезка [-7;-3] y=f(x ) принимает наименьшее значение.](https://fsd.videouroki.net/html/2014/10/29/98690319/img34.jpg)
На рисунке изображен график производной функции y=f(x ) , определенной на интервале (-8;4) . В какой точке отрезка [-7;-3] y=f(x ) принимает наименьшее значение.
![На рисунке изображен график производной функции y=f(x ) , определенной на интервале (-8;3) . В какой точке отрезка [-3;-2] y=f(x ) принимает наибольшее значение.](https://fsd.videouroki.net/html/2014/10/29/98690319/img35.jpg)
На рисунке изображен график производной функции y=f(x ) , определенной на интервале (-8;3) . В какой точке отрезка [-3;-2] y=f(x ) принимает наибольшее значение.

Какие выводы мы можем сделать, когда дан график производной функции?
6. Можем найти абсциссу точки, в которой касательная к графику параллельна оси абсцисс или совпадает с ней.
7. Можем найти количество точек, в которых касательная к графику функции параллельна прямой или совпадает с ней.
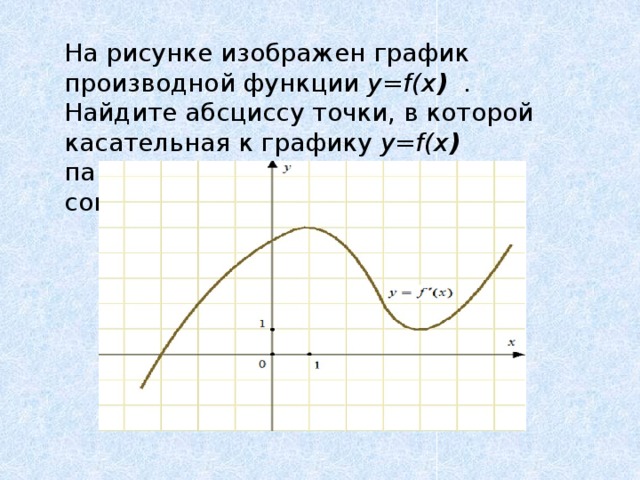
На рисунке изображен график производной функции y=f(x ) . Найдите абсциссу точки, в которой касательная к графику y=f(x ) параллельна оси абсцисс или совпадает с ней.
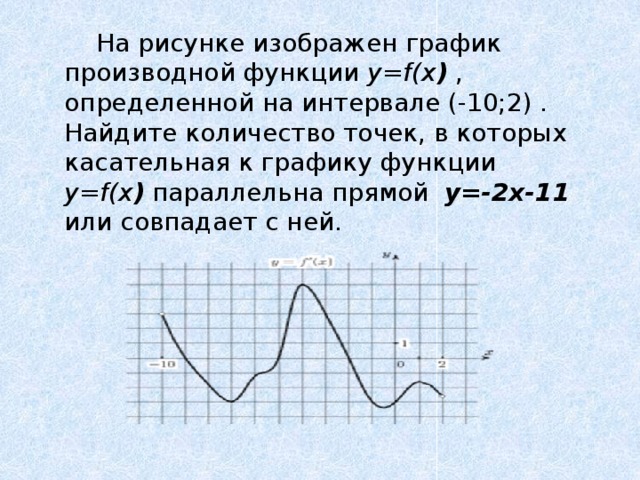
На рисунке изображен график производной функции y=f(x ) , определенной на интервале (-10;2) . Найдите количество точек, в которых касательная к графику функции y=f(x ) параллельна прямой y=-2x-11 или совпадает с ней.


 Получите свидетельство
Получите свидетельство Вход
Вход

































![На рисунке изображен график производной функции y=f(x ) , определенной на интервале (-4;8) . Найдите точку экстремума функции на отрезке [-2;6]](https://fsd.videouroki.net/html/2014/10/29/98690319/img30.jpg)
![На рисунке изображен график производной функции y=f(x ) , определенной на интервале (-18;6) . Найдите количество точек минимума функции на отрезке [-13;1] .](https://fsd.videouroki.net/html/2014/10/29/98690319/img31.jpg)
![На рисунке изображен график производной функции y=f(x ) , определенной на интервале (-11;11) . Найдите количество точек экстремума функции y=f(x ) на отрезке [-10;10] .](https://fsd.videouroki.net/html/2014/10/29/98690319/img32.jpg)

![На рисунке изображен график производной функции y=f(x ) , определенной на интервале (-8;4) . В какой точке отрезка [-7;-3] y=f(x ) принимает наименьшее значение.](https://fsd.videouroki.net/html/2014/10/29/98690319/img34.jpg)
![На рисунке изображен график производной функции y=f(x ) , определенной на интервале (-8;3) . В какой точке отрезка [-3;-2] y=f(x ) принимает наибольшее значение.](https://fsd.videouroki.net/html/2014/10/29/98690319/img35.jpg)












 Презентация по математике "Подготовка к ЕГЭ. Графики функции, производных функций. Исследование функций" (1.43 MB)
Презентация по математике "Подготовка к ЕГЭ. Графики функции, производных функций. Исследование функций" (1.43 MB)
 0
0 1259
1259 84
84 Нравится
0
Нравится
0


