
Разложение многочленов на множители.
Обобщающий урок по теме «Разложение на множители»
7 КЛАСС
В.И. Синявский. ГУО «Гимназия № 19 г. Минска»

Немного теории
Разложить многочлен на множители значит представить его в виде произведения более простых многочленов.
Существует несколько способов разложения:
- Вынесение общего множителя за скобки
- Способ группировки
- С помощью формул сокращенного умножения
Сначала убедимся в том что разложение на множители –вещь полезная.
Вам предлагают решить уравнение 2х 2 +х-6=0.
Для таких уравнений имеется специальное правило решения, но вы его пока еще не знаете.
Как быть?

Воспользуемся разложением многочлена на множители: 2х 2 +х –6=(2х-3)(х+2)
Тогда заданное уравнение можно переписать в виде:
(2х-3) (х+2)=0
Произведение равно нулю, если один из множителей равен нулю. Значит,
либо 2х-3=0,
либо х+2=0.
Из первого уравнения х=1,5, а из второго уравнения х=-2.
Уравнение решено, оно имеет два корня: 1,5 и –2.

Рассмотрим другую ситуацию
Пусть нужно найти значение числового выражения
53 2 -47 2
61 2 -39 2
Самое эффективное решение – дважды воспользоваться формулой разности квадратов:
53 2 -47 2 = (53-47)(53+47) = 6 •100 = 6 = 3
61 2 -39 2 (61-39)(61+39) 22•100 22 11
Разложение на множители позволило нам сократить дробь. Позднее мы оценим это и при выполнении действий с алгебраическими дробями.

Таким образом, разложение многочлена на множители используется для решения уравнений, для преобразования числовых и алгебраических выражений. Применяется оно и в других ситуациях, как, скажем, в следующем довольно трудном, но красивом примере, где ключ к успеху опять-таки в разложении на множители .
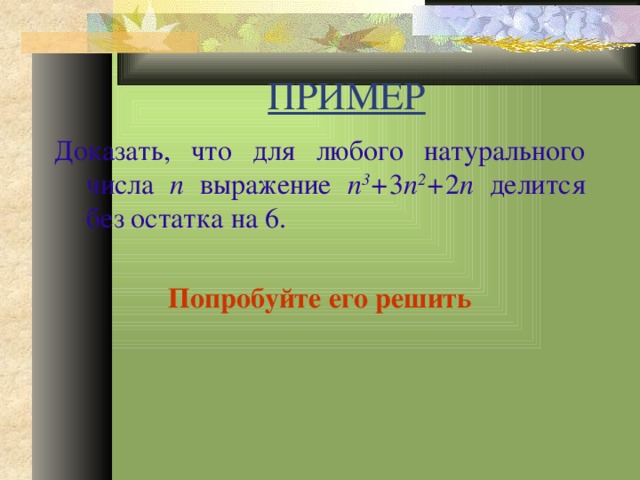
ПРИМЕР
Доказать, что для любого натурального числа n выражение n 3 + 3 n 2 + 2 n делится без остатка на 6.
Попробуйте его решить
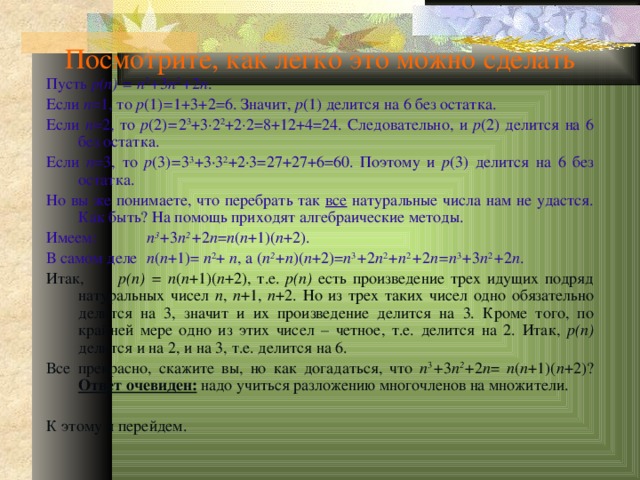
Посмотрите, как легко это можно сделать
Пусть p(n) = n 3 + 3 n 2 + 2 n .
Если n =1, то p (1) = 1+3+2=6. Значит, p (1) делится на 6 без остатка.
Если n =2, то p (2) = 2 3 +3 ·2 2 +2·2=8+12+4=24. Следовательно, и p (2) делится на 6 без остатка.
Если n =3, то p (3) = 3 3 +3·3 2 +2·3=27+27+6=60. Поэтому и p (3) делится на 6 без остатка.
Но вы же понимаете, что перебрать так все натуральные числа нам не удастся. Как быть? На помощь приходят алгебраические методы.
Имеем: n 3 + 3 n 2 + 2 n = n ( n +1)( n +2).
В самом деле n ( n +1)= n 2 + n , а ( n 2 +n )( n +2)= n 3 + 2 n 2 +n 2 + 2 n=n 3 + 3 n 2 + 2 n .
Итак, p(n) = n ( n +1)( n +2), т.е. p(n) есть произведение трех идущих подряд натуральных чисел n , n +1, n +2. Но из трех таких чисел одно обязательно делится на 3, значит и их произведение делится на 3. Кроме того, по крайней мере одно из этих чисел – четное, т.е. делится на 2. Итак, p(n) делится и на 2, и на 3, т.е. делится на 6.
Все прекрасно, скажите вы, но как догадаться, что n 3 + 3 n 2 + 2 n = n ( n +1)( n +2)? Ответ очевиден: надо учиться разложению многочленов на множители.
К этому и перейдем.

Вынесение общего множителя за скобки Алгоритм отыскания общего множителя нескольких одночленов
- Найти наибольший общий делитель коэффициентов всех одночленов, входящих в многочлен, - он и будет общим числовым множителем (разумеется, это относится только к случаю целочисленных коэффициентов).
- Найти переменные, которые входят в каждый член многочлена, и выбрать для каждой из них наименьший (из имеющихся) показатель степени.
- Произведение коэффициента, найденного на первом шаге, является общим множителем, который целесообразно вынести за скобки.

Пример Разложить на множители: - x 4 y 3 - 2 x 3 y 2 + 5 x 2 .
Воспользуемся сформулированным алгоритмом .
- Наибольший общий делитель коэффициентов –1, -2 и 5 равен 1.
- Переменная x входит во все члены многочлена с показателями соответственно 4, 3, 2; следовательно, можно вынести за скобки x 2 .
- Переменная y входит не во все члены многочлена; значит, ее нельзя вынести за скобки.
Вывод: за скобки можно вынести x 2 . Правда, в данном случае целесообразнее вынести - x 2 . Получим:
-x 4 y 3 - 2 x 3 y 2 + 5 x 2 =-x 2 (x 2 y 3 + 2 xy 2 - 5).
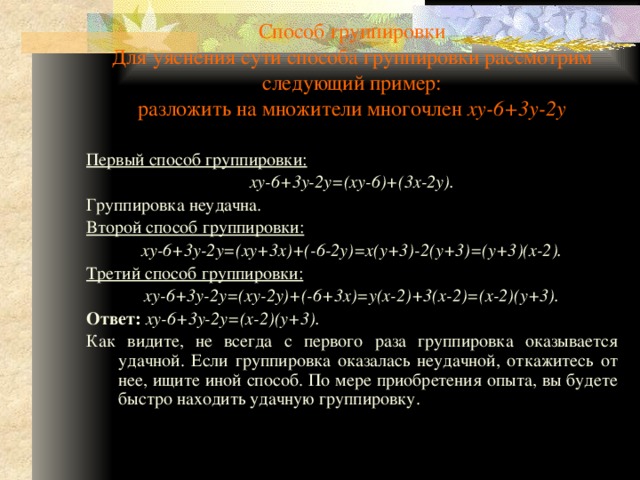
Способ группировки Для уяснения сути способа группировки рассмотрим следующий пример: разложить на множители многочлен xy-6+3y-2y
Первый способ группировки:
xy-6+3y-2y=(xy-6)+(3x-2y).
Группировка неудачна.
Второй способ группировки:
xy-6+3y-2y=(xy+3x)+(-6-2y)=x(y+3)-2(y+3)=(y+3)(x-2).
Третий способ группировки:
xy-6+3y-2y=(xy-2y)+(-6+3x)=y(x-2)+3(x-2)=(x-2)(y+3).
Ответ: xy-6+3y-2y=(x-2)(y+3).
Как видите, не всегда с первого раза группировка оказывается удачной. Если группировка оказалась неудачной, откажитесь от нее, ищите иной способ. По мере приобретения опыта, вы будете быстро находить удачную группировку.

Разложение многочлена на множители с помощью формул сокращенного умножения Вспомните эти формулы :
a 2 -b 2 =(a-b)(a+b);
a 3 -b 3 =(a-b)(a 2 +ab+b 2 );
a 3 +b 3 =(a+b)(a 2 -ab+b 2 );
a 2 +2ab+b 2 =(a+b) 2 ;
a 2 -2ab+b 2 =(a-b) 2 .
Первую из этих формул можно применять к выражению, представляющему собой разность квадратов (безразлично чего – чисел, одночленов, многочленов), вторую и третью – к выражению, представляющему собой разность (или сумму ) кубов; последние две формулы применяются к трехчлену, представляющему собой полный квадрат , т.е. содержащему сумму квадратов двух выражений и удвоенное произведение тех же выражений.

Примеры Разложить на множители:
1) x 6 -4a 4 . Воспользуемся первой формулой (разность квадратов):
x 6 -4a 4 =(x 3 ) 2 -(2a 2 ) 2 =(x 2 -2a 2 )(x 3 +2a 2 ).
2) a 6 +27b 3 . Воспользуемся третьей формулой (сумма кубов):
a 6 +27b 3 =(a 2 ) 3 +(3b) 3 =(a 2 +3b)((a 2 ) 2 -a 2 ·3b+(3b) 2 )= =(a 2 +3b)(a 4 -3a 2 b+9b 4 ).
3) a 2 -4ab+4b 2 . В этом примере дан трехчлен, для его разложения на множители будем пользоваться пятой формулой, если, конечно, убедимся в том, что трехчлен является полным квадратом:
a 2 -4ab+4b 2 =a 2 +(2b) 2 -2·a·2b=(a-2b) 2 .
Мы убедились, что трехчлен содержит сумму квадратов одночленов a и 2 b , а также удвоенное произведение этих одночленов. Значит, это полный квадрат, причем квадрат разности.

Разложение многочлена на множители с помощью комбинации различных приемов
- В математике не так часто бывает, чтобы при решении примера применялся только один прием, чаще встречаются комбинированные примеры, где сначала используется один прием, затем другой и т.д. Чтобы успешно решать такие примеры, мало знать сами приемы, надо еще уметь выработать план их последовательного применения. Иными словами, здесь нужны не только знания, но и опыт. Вот такие комбинированные примеры мы и рассмотрим.

Пример 1 Разложить на множители многочлен 36a 6 b 3 -96a 4 b 4 +64a 2 b 5
1) Сначала займемся вынесением общего множителя за скобки. Рассмотрим коэффициенты 36, 96, 64. Все они делятся на 4, причем это – наибольший общий делитель, вынесем его за скобки. Во все члены многочлена входит переменная a (соответственно a 6 , a 4 , a 2 ), поэтому за скобки можно вынести a 2 . Точно так же во все члены многочлена входит переменная b (соответственно b 3 , b 4 , b 5 ) – за скобки можно вынести b 3 .
Итак, за скобки вынесем 4a 2 b 3 . Тогда получим:
36a 6 b 3 -96a 4 b 4 +64a 2 b 5 =4a 2 b 3 (9a 4 -24a 2 b+16b 2 ).
2) Рассмотрим трехчлен в скобках: 9a 4 -24a 2 b+16b 2 . Выясним, не является ли он полным квадратом. Имеем:
9a 4 -24a 2 b+16b 2 =(3a 2 ) 2 +(4b) 2 -2 ·3a 2 ·4b .
Все условия полного квадрата соблюдены, следовательно,
9a 4 -24a 2 b+16b 2 =(3a 2 -4b) 2 .
3) Комбинируя два приема (вынесение общего множителя за скобки и использование формул сокращенного умножения), получаем окончательный результат:
36a 6 b 3 -96a 4 b 4 +64a 2 b 5 =4a 2 b 3 (3a 2 -4b) 2 .

Пример 2 Разложить на множители x 4 +x 2 a 2 +a 4
Применим метод выделения полного квадрата. Для этого представим x 2 a 2 в виде 2x 2 a 2 -x 2 a 2 . Получим:
x 4 +x 2 a 2 +a 4 =x 4 +2x 2 a 2 -x 2 a 2 +a 4 =
=(x 4 +2x 2 a 2 +a 4 )-x 2 a 2 =
=(x 2 +a 2 ) 2 -(xa) 2 =(x 2 +a 2 +xa).

Пример 3 Разложить на множители n 3 +3n 2 +2n
Сначала воспользуемся тем, что n можно вынести за скобки: n(n 2 +3n+2). Теперь к трехчлену n 2 +3n+2 применим способ группировки, предварительно представив 3n в виде 2n+n . Получим:
n 2 +3n+2=n 2 +2n+n+2=(n 2 +2n)+(n+2)=
=n(n+2)+(n+2)=(n+2)(n+1).
Окончательно получаем:
n 2 +3n+2=n(n+1)(n+2).

Пример 4 Решить уравнение x 2 -6x+5=0
Первый способ. Представим – 6x в виде суммы –x-5x, а затем применим способ группировки:
x 2 -6x+5=x 2 -5x+5=(x 2 -x)+(-5x+5)=x(x-1)-5(x-1)=(x-1)(x-5).
Тогда заданное уравнение примет вид:
(x-1)(x-5)=0,
откуда находим, что либо x=1, либо x=5.
Второй способ. Применим метод выделения полного квадрата, для чего представим слагаемое 5 в виде 9-4. Получим:
x 2 -6x+5=x 2 -6x+9-4=(x 2 -6x+9)-4=
=(x-3) 2 -2 2 =(x-3-2)(x-3+2)=(x-5)(x-1).
Снова пришли к уравнению (x-1)(x-5)=0, имеющему корни 1 и 5.
Ответ: 1, 5.

Сокращение алгебраических дробей
Алгебраической дробью называется отношение двух многочленов P и Q . При этом используют запись P
Q

Тождества
a 2 -b 2 =(a-b)(a+b);
x 2 -4x+4=(x-2) 2 ;
(a+b)c=ac+bc.
Написанные равенства верны при любых значениях входящих в их состав переменных. Такие равенства называют тождествами . Левую и правую часть тождества называют выражениями, тождественно равными . Замену одного выражения другим, тождественным ему, называют тождественным преобразованием выражения.
Определение. Тождество – это равенство, верное при любых допустимых значениях входящих в его состав переменных.

ОСНОВНЫЕ РЕЗУЛЬТАТЫ
- Мы ввели новые (для вас) понятия математического языка:
разложение многочлена на множители;
алгебраическая дробь, сокращение алгебраической дроби;
тождество, тождественно равные выражения, тождественное преобразование выражения.
- Вы познакомились со следующими приемами разложения многочлена на множители:
вынесение общего множителя за скобки;
группировка;
использование формул сокращенного умножения;
выделение полного квадрата.

На этом мы и закончим
наш сегодняшний урок


 Получите свидетельство
Получите свидетельство Вход
Вход


































 Презентация по математике по теме "Разложение многочленов на множители" (0.37 MB)
Презентация по математике по теме "Разложение многочленов на множители" (0.37 MB)
 1
1 609
609 57
57 Нравится
0
Нравится
0


