Презентация по математике по теме: "Призма"

Тип урока: урок изучения нового материала.

Цели урока:

Обучающая: продолжить систематическое изучение многогранников, в ходе решения задач на нахождение объема наклонной призмы.

Развивающая: развитие индуктивных и дедуктивных навыков мышления.

Воспитательная: привитие навыков активной учебной деятельности, формирование навыков самостоятельного поиска и отбора информации. Создание условий для исследовательской деятельности учащихся, демонстрация приемов такой деятельности

Формы работы на уроке: коллективная, устная, письменная.

Оборудование: мультимедийный проектор, компьютер, презентация, модели наклонных призм, сделанных учащимися.

Структура урока:

1. Организационный момент, постановка домашнего задания
2. Повторение изученного материала и подготовка к усвоению нового материала
3. Проверка домашнего задания, перетекающая в изучение нового материала
4. Первичное закрепление
5. Применение изучаемого материала в реальной жизни
6. Организация процесса усвоения знаний в ходе выполнения практической работы
7. Итоги работы, рефлексия

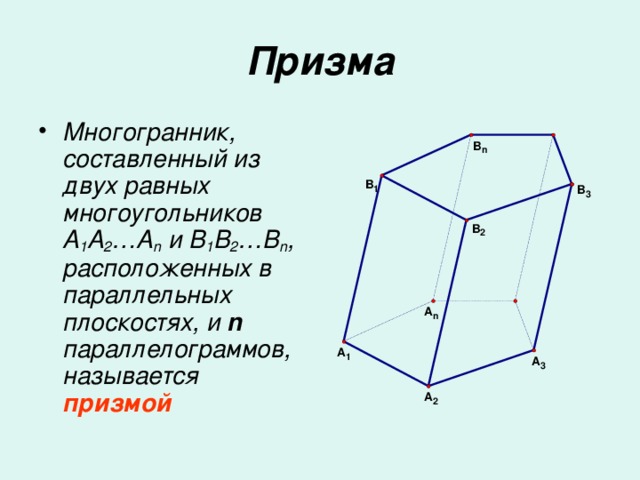
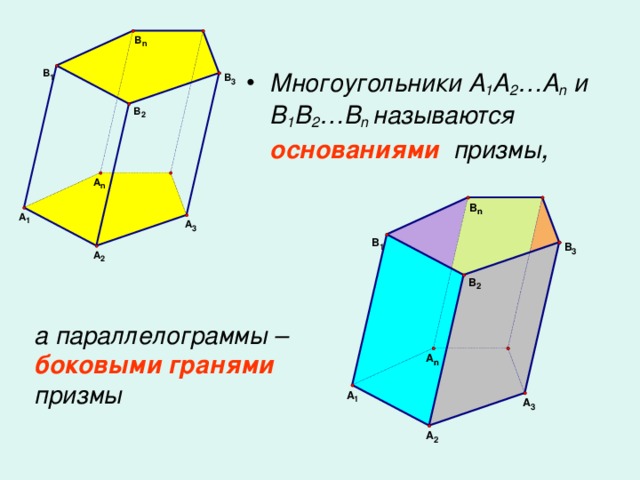
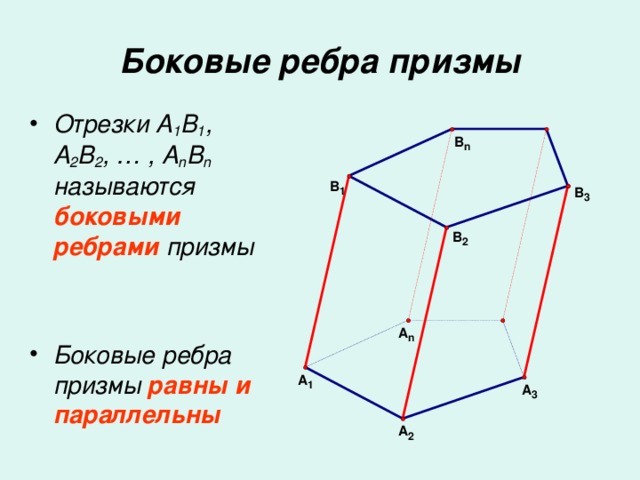
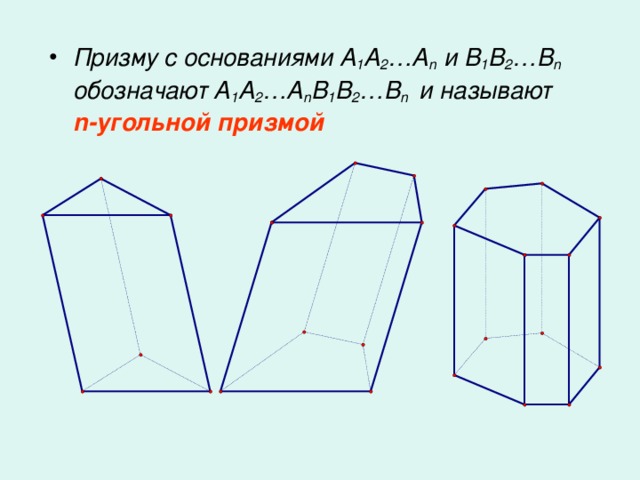
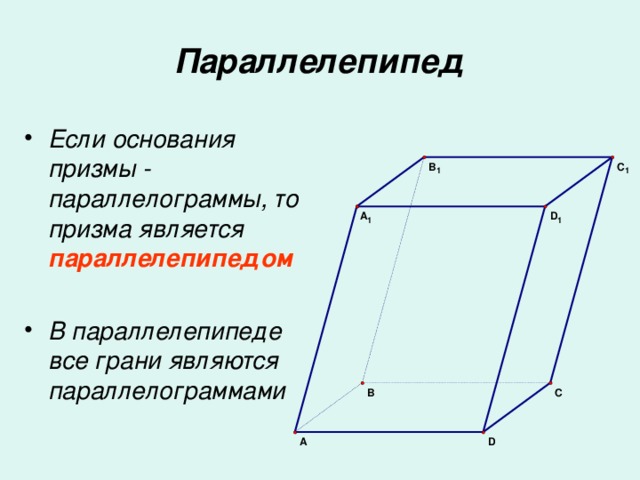
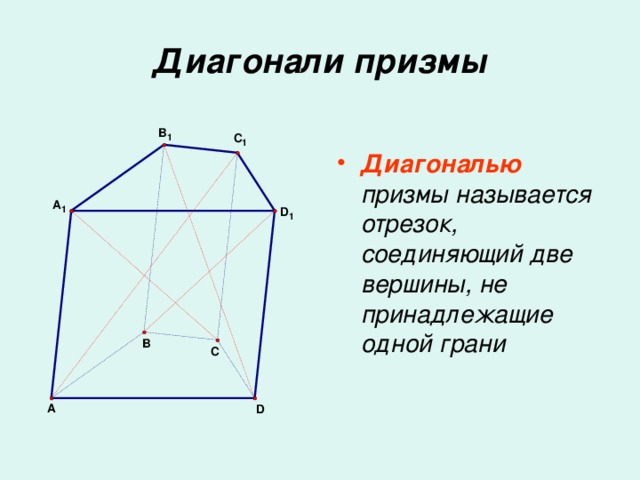
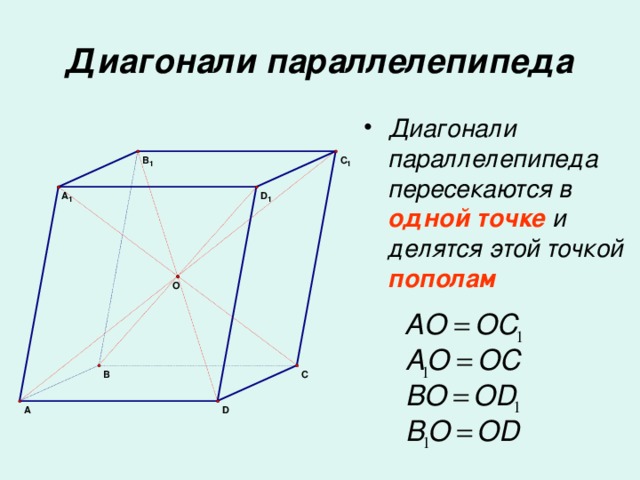
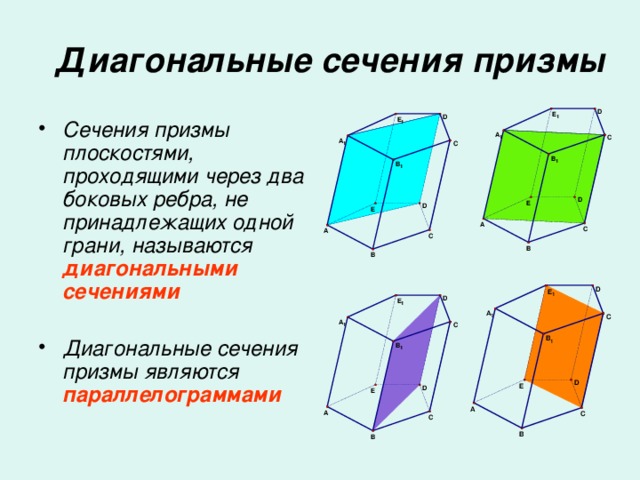
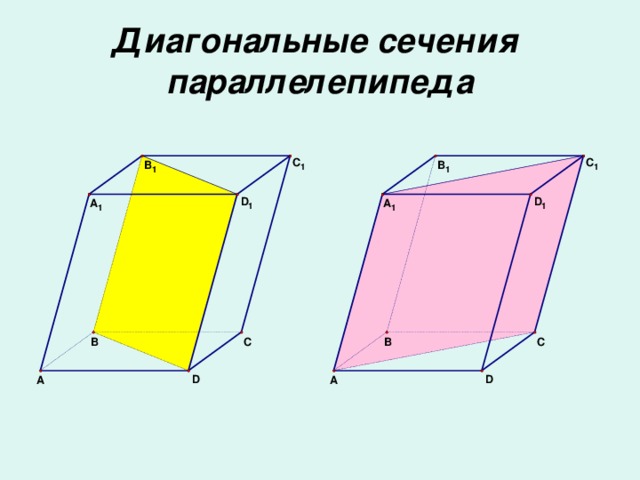
Многогранник, составленный из двух равных многоугольников A1A2…An и B1B2…Bn, расположенных в параллельных плоскостях, и n параллелограммов, называется призмой.

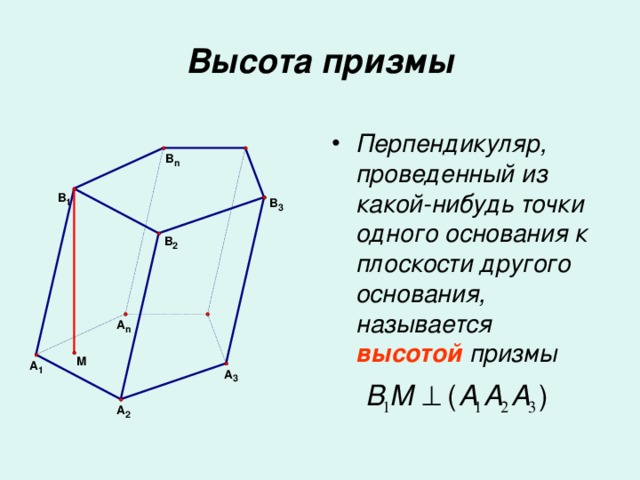
Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания, называется высотой призмы.

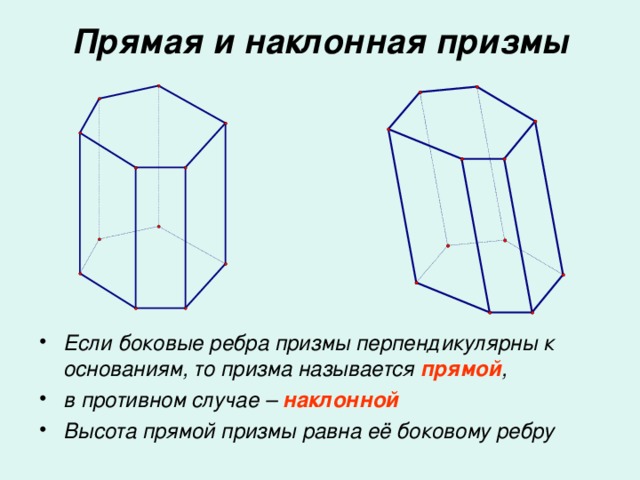
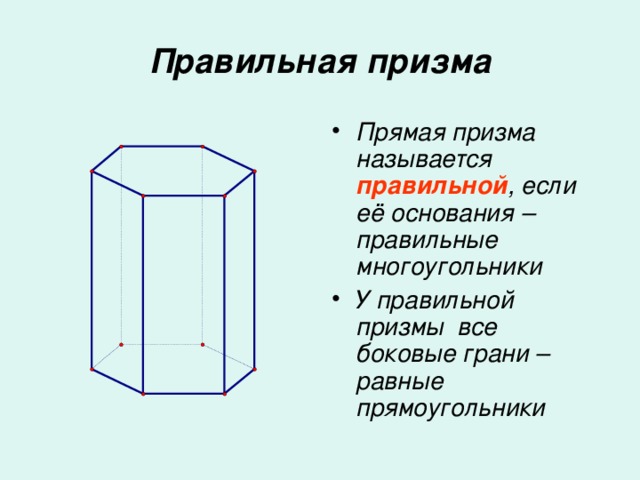
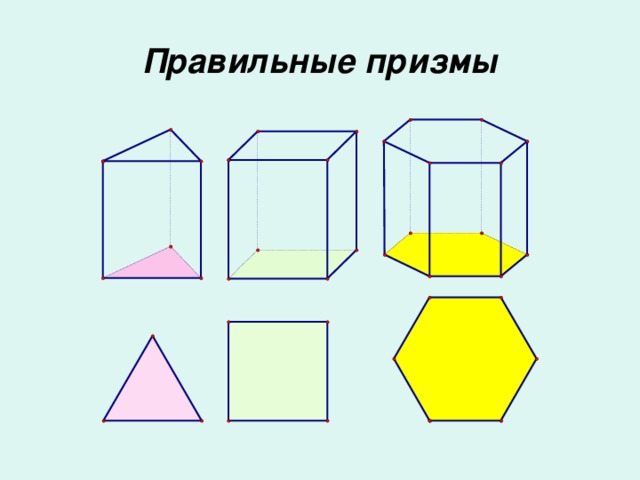
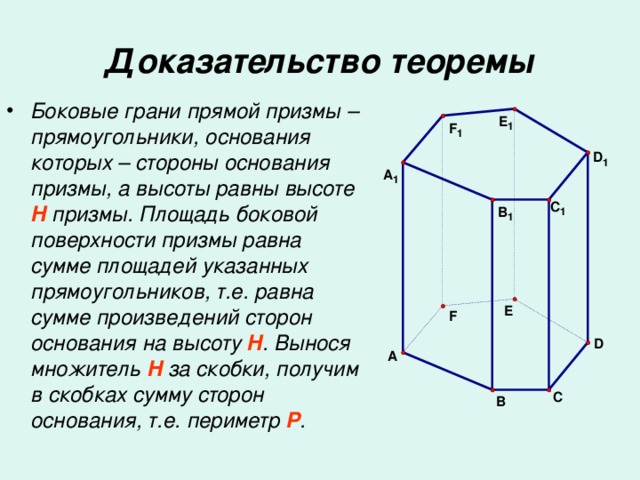
Прямая призма называется правильной, если её основания – правильные многоугольники.

У правильной призмы  все боковые грани – равные прямоугольники.

Призма

• Многогранник, составленный из двух равных многоугольников A 1 A 2 …A n и B 1 B 2 …B n , расположенных в параллельных плоскостях, и n параллелограммов, называется призмой

• Многоугольники A 1 A 2 …A n и B 1 B 2 …B n называются основаниями призмы ,

а параллелограммы – боковыми гранями призмы

Боковые ребра призмы

• Отрезки A 1 B 1 , A 2 B 2 , … , A n B n называются боковыми ребрами призмы

• Боковые ребра призмы равны и параллельны

• Призму с основаниями A 1 A 2 …A n и B 1 B 2 …B n обозначают A 1 A 2 …A n B 1 B 2 …B n и называют n -угольной призмой

Высота призмы

• Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания, называется высотой призмы

Прямая и наклонная призмы

• Если боковые ребра призмы перпендикулярны к основаниям, то призма называется прямой ,
• в противном случае – наклонной
• Высота прямой призмы равна её боковому ребру

Правильная призма

• Прямая призма называется правильной , если её основания – правильные многоугольники
• У правильной призмы все боковые грани – равные прямоугольники

Правильные призмы

Параллелепипед

• Если основания призмы - параллелограммы, то призма является параллелепипедом

• В параллелепипеде все грани являются параллелограммами

Диагонали призмы

• Диагональю призмы называется отрезок, соединяющий две вершины, не принадлежащие одной грани

Диагонали параллелепипеда

• Диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам

Диагональные сечения призмы

• Сечения призмы плоскостями, проходящими через два боковых ребра, не принадлежащих одной грани, называются диагональными сечениями

• Диагональные сечения призмы являются параллелограммами

Диагональные сечения параллелепипеда

Площадь поверхности призмы

• Площадью полной поверхности призмы называется сумма площадей всех её граней
• Площадью боковой поверхности призмы называется сумма площадей её боковых граней

Теорема о площади боковой поверхности прямой призмы

Теорема .

Площадь боковой поверхности прямой призмы равна произведению периметра основания на высоту призмы

Доказательство теоремы

• Боковые грани прямой призмы – прямоугольники, основания которых – стороны основания призмы, а высоты равны высоте H призмы. Площадь боковой поверхности призмы равна сумме площадей указанных прямоугольников, т.е. равна сумме произведений сторон основания на высоту H . Вынося множитель H за скобки, получим в скобках сумму сторон основания, т.е. периметр P .