
Критические точки функции Точки экстремумов
Выполнила: Тулекова Вадиля студентка ПСЭК
Петропавловск 2016 г.
Точки экстремума
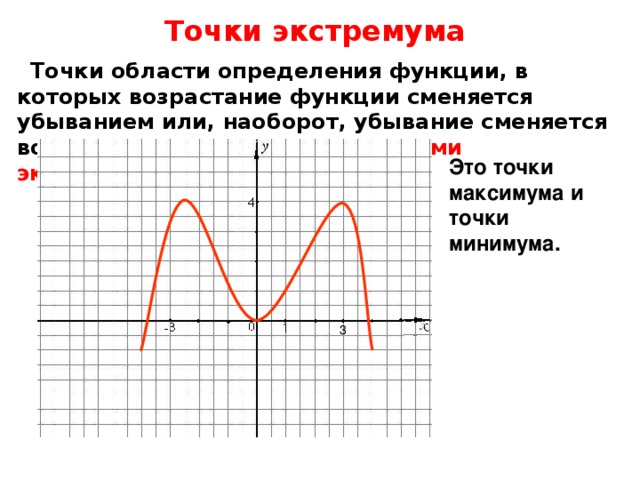
Точки области определения функции, в которых возрастание функции сменяется убыванием или, наоборот, убывание сменяется возрастанием, называются точками экстремумов.
Это точки максимума и точки минимума.
3
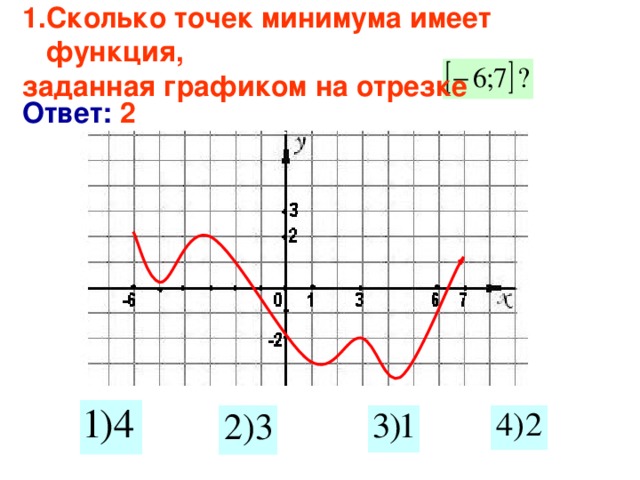
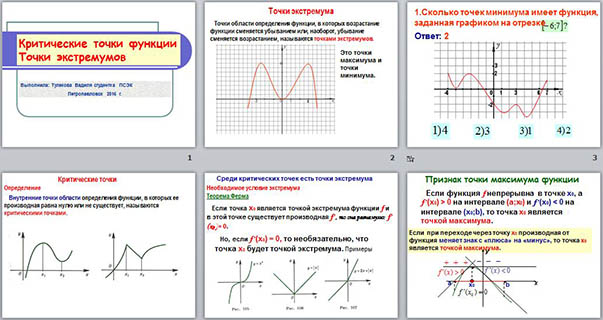
- Сколько точек минимума имеет функция,
заданная графиком на отрезке
Ответ: 2
Критические точки
Определение
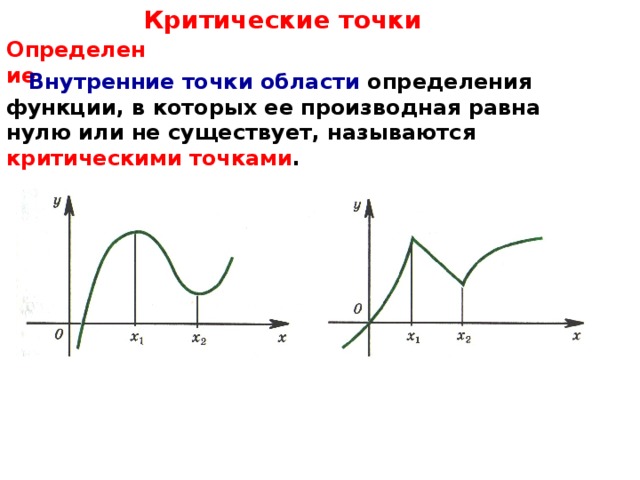
Внутренние точки области определения функции, в которых ее производная равна нулю или не существует, называются критическими точками .
Среди критических точек есть точки экстремума
Необходимое условие экстремума
Теорема Ферма
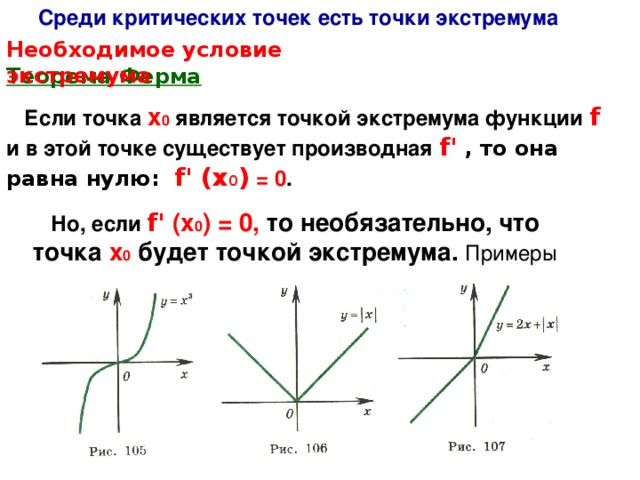
Если точка х 0 является точкой экстремума функции f и в этой точке существует производная f ' , то она равна нулю: f' (х 0 ) = 0 .
Но, если f' (х 0 ) = 0, то необязательно, что точка х 0 будет точкой экстремума. Примеры
 0 на интервале (а;х 0 ) и f' (х 0 ) на интервале (х 0 ; b ), то точка х 0 является точкой максимума . Если при переходе через точку х 0 производная от функция меняет знак с «плюса» на «минус», то точка х 0 является точкой максимума . y х а b х 0 " width="640"
0 на интервале (а;х 0 ) и f' (х 0 ) на интервале (х 0 ; b ), то точка х 0 является точкой максимума . Если при переходе через точку х 0 производная от функция меняет знак с «плюса» на «минус», то точка х 0 является точкой максимума . y х а b х 0 " width="640"
Признак точки максимума функции
Если функция f непрерывна в точке х 0 , а f' (х 0 ) 0 на интервале (а;х 0 ) и f' (х 0 ) на интервале (х 0 ; b ), то точка х 0 является точкой максимума .
Если при переходе через точку х 0 производная от функция меняет знак с «плюса» на «минус», то точка х 0 является точкой максимума .
y
х
а
b
х 0
 0 на интервале (х 0 ; b ), то точка х 0 является точкой минимума . Если при переходе через точку х 0 производная от функции меняет знак с «минуса» на «плюс», то точка х 0 является точкой минимума. y х х 0 а b " width="640"
0 на интервале (х 0 ; b ), то точка х 0 является точкой минимума . Если при переходе через точку х 0 производная от функции меняет знак с «минуса» на «плюс», то точка х 0 является точкой минимума. y х х 0 а b " width="640"
Признак точки минимума функции
Если функция f непрерывна в точке х 0 , а f' (х 0 ) на интервале (а;х 0 ) и f' (х 0 ) 0 на интервале (х 0 ; b ), то точка х 0 является точкой минимума .
Если при переходе через точку х 0 производная от функции меняет знак с «минуса» на «плюс», то точка х 0 является точкой минимума.
y
х
х 0
а
b

 Получите свидетельство
Получите свидетельство Вход
Вход









 0 на интервале (а;х 0 ) и f' (х 0 ) на интервале (х 0 ; b ), то точка х 0 является точкой максимума . Если при переходе через точку х 0 производная от функция меняет знак с «плюса» на «минус», то точка х 0 является точкой максимума . y х а b х 0 " width="640"
0 на интервале (а;х 0 ) и f' (х 0 ) на интервале (х 0 ; b ), то точка х 0 является точкой максимума . Если при переходе через точку х 0 производная от функция меняет знак с «плюса» на «минус», то точка х 0 является точкой максимума . y х а b х 0 " width="640"
 0 на интервале (х 0 ; b ), то точка х 0 является точкой минимума . Если при переходе через точку х 0 производная от функции меняет знак с «минуса» на «плюс», то точка х 0 является точкой минимума. y х х 0 а b " width="640"
0 на интервале (х 0 ; b ), то точка х 0 является точкой минимума . Если при переходе через точку х 0 производная от функции меняет знак с «минуса» на «плюс», то точка х 0 является точкой минимума. y х х 0 а b " width="640"









 Презентация по математике "Критические точки функции. Точки экстремумов" (0.62 MB)
Презентация по математике "Критические точки функции. Точки экстремумов" (0.62 MB)
 1
1 2930
2930 406
406



Спасибо!