Презентация по математике "И это все о нём. Треугольник"

Треугольник был символом геометрии в течении двух с половиной тысяч лет; но кроме этого треугольник - атом геометрии.

Три точки и три отрезка, соединяющие эти точки попарно, определяют геометрическую фигуру, которая называется треугольником.

История появления треугольников.

Первые упоминания о треугольнике и его свойствах ученые находят в египетских папирусах, которым более 4000 лет. В Древней Греции изучение свойств треугольника достигает высокого уровня – это теорема Пифагора и формула Герона, которым более 2000 лет.

В XV - XVI веках появилось огромное количество исследований свойств треугольника. Это большой раздел планиметрии, получивший название «Новая геометрия треугольника». Большой вклад в изучение свойств треугольника внес русский ученый Н. И. Лобачевский.

Египетский треугольник.

Прямоугольный треугольник с соотношением сторон 3:4:5. сумма указанных чисел (3+4+5=12) с древних времен использовалась как единица кратности при построении прямых углов с помощью веревки, размеченной узлами на 3/12 и 7/12 ее длины. Применялся в архитектуре средних веков для построения схем пропорциональности.

Виды треугольников.

Треугольники бывают остроугольные, прямоугольные и тупоугольные.

Ты на меня, ты на него,

На всех нас посмотри.

У нас всего, у нас всего,

У нас всего по три.

Три стороны и три угла,

И столько же вершин.

И трижды трудные дела

Мы трижды совершим.

Все в нашем городе друзья,

Дружнее не сыскать.

Мы треугольников семья,

Нас каждый должен знать .

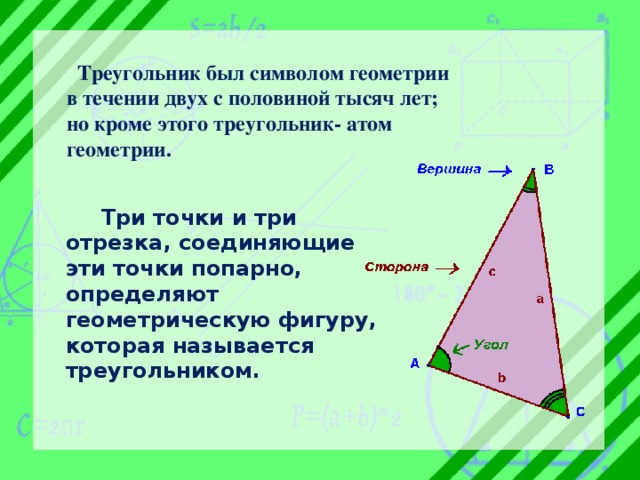
Треугольник был символом геометрии в течении двух с половиной тысяч лет; но кроме этого треугольник- атом геометрии.

Три точки и три отрезка, соединяющие эти точки попарно, определяют геометрическую фигуру, которая называется треугольником.

История появления треугольников.

Первые упоминания о треугольнике и его свойствах ученые находят в египетских папирусах, которым более 4000 лет. В Древней Греции изучение свойств треугольника достигает высокого уровня – это теорема Пифагора и формула Герона, которым более 2000 лет.

В XV - XVI веках появилось огромное количество исследований свойств треугольника. Это большой раздел планиметрии, получивший название «Новая геометрия треугольника». Большой вклад в изучение свойств треугольника внес русский ученый Н.И.Лобачевский.

Египетский треугольник

Прямоугольный треугольник с соотношением сторон 3:4:5. сумма указанных чисел (3+4+5=12) с древних времен использовалась как единица кратности при построении прямых углов с помощью веревки, размеченной узлами на 3/12 и 7/12 ее длины. Применялся в архитектуре средних веков для построения схем пропорциональности.

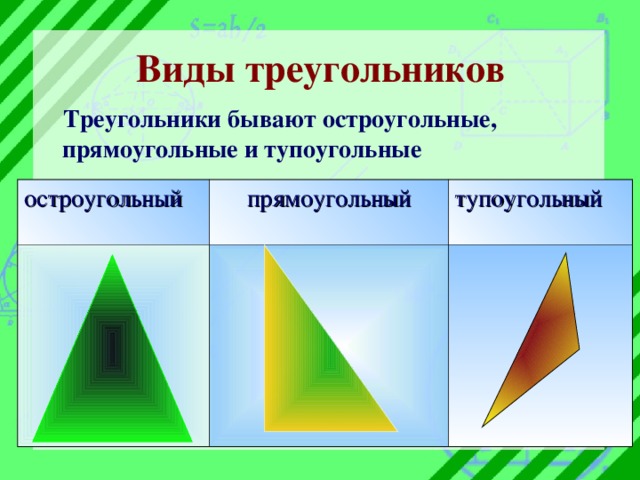
Виды треугольников

Треугольники бывают остроугольные, прямоугольные и тупоугольные

остроугольный

прямоугольный

тупоугольный

Виды треугольников

разносторонние

равнобедренные

равносторонние

Треугольник

- все стороны которого равны, называется равносторонним;

-с разными сторонами – называется разносторонним.

Треугольник называется равнобедренным, если две его стороны равны. Равные стороны называются боковыми сторонами,

а третья сторона – основанием равнобедренного треугольника.

Высота равнобедренного треугольника, проведенная к основанию, является его медианой и биссектрисой.

Биссектрисы треугольника

1

2

Медианы треугольника

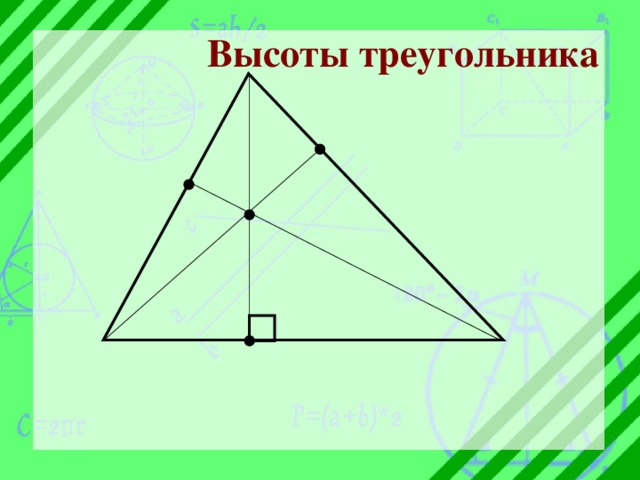
Высоты треугольника

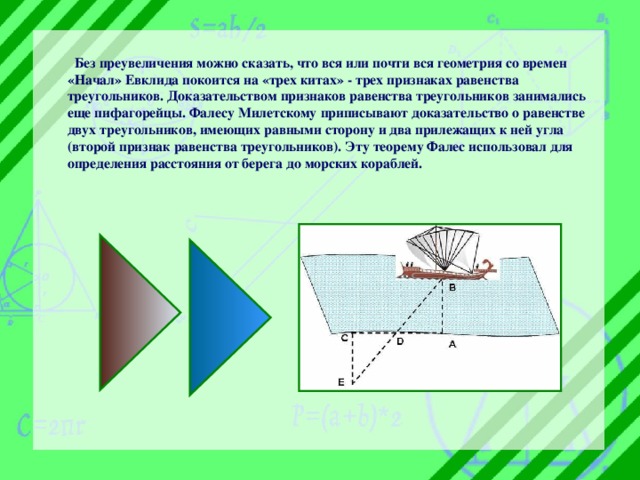
Без преувеличения можно сказать, что вся или почти вся геометрия со времен «Начал» Евклида покоится на «трех китах» - трех признаках равенства треугольников. Доказательством признаков равенства треугольников занимались еще пифагорейцы. Фалесу Милетскому приписывают доказательство о равенстве двух треугольников, имеющих равными сторону и два прилежащих к ней угла (второй признак равенства треугольников). Эту теорему Фалес использовал для определения расстояния от берега до морских кораблей.

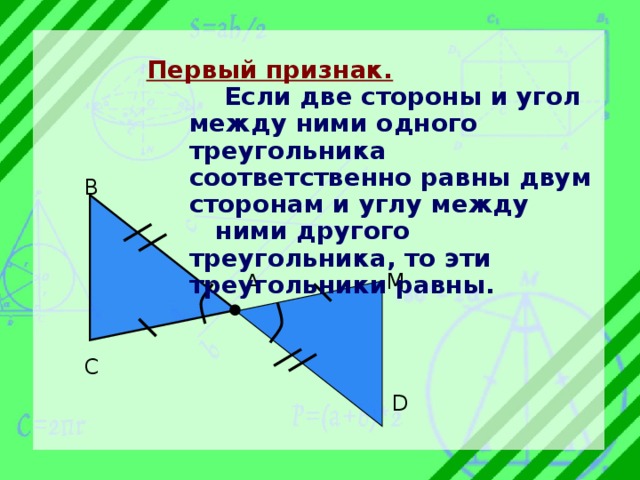
Первый признак.

Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между

ними другого треугольника, то эти треугольники равны.

В

М

А

С

D

В

С

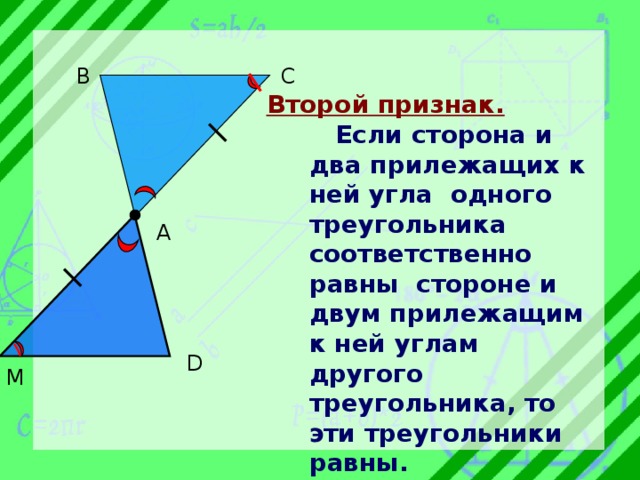
Второй признак.

Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то эти треугольники равны.

А

D

М

.

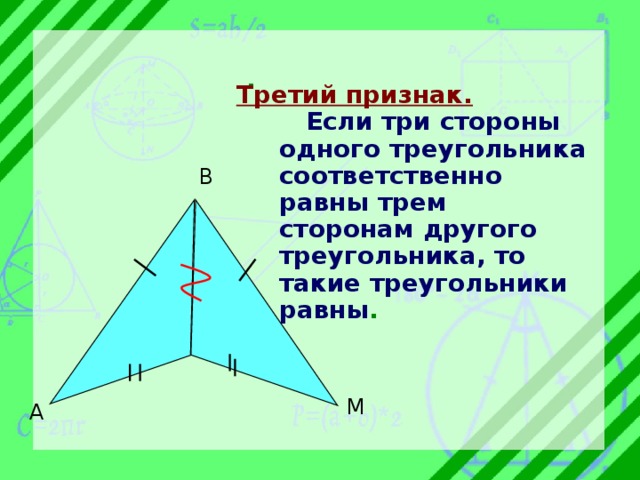
Третий признак.

Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны .

B

K

M

A

13

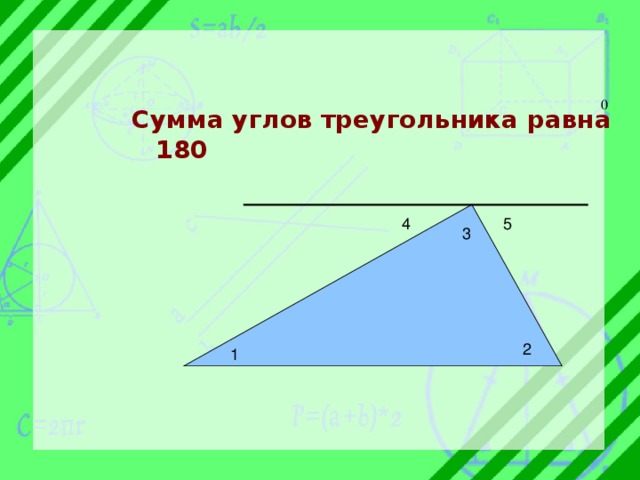
Сумма углов треугольника равна 180

4

5

3

2

1

Треугольник Паскаля

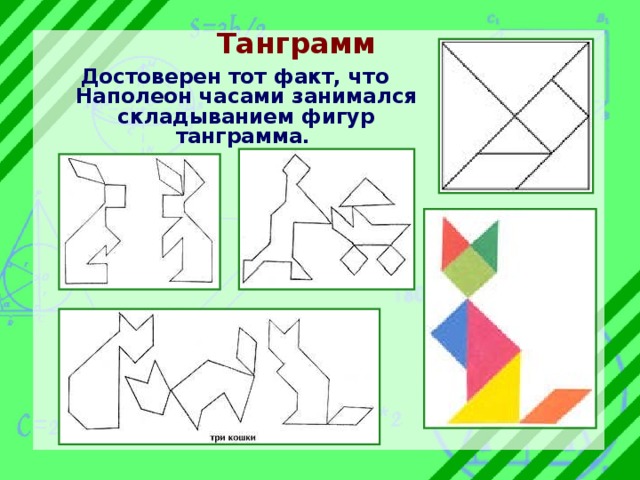
Танграмм

Достоверен тот факт, что Наполеон часами занимался складыванием фигур танграмма.

Созвездие «Треугольник»

Треугольник в религии

Лоскутное шитье

Треугольные украшения

Треугольники в кулинарии

Мода и треугольники

Жесткость – это

неспособность

изменить форму, не меняя сторон.

Треугольники в архитектуре

1.Делая садовую калитку,

обязательно прибиваем

планку или доску, чтобы

получить треугольник.

Это придает калитке прочность.

2.Стропила зданий имеют вид треугольников.

Это придает им крепость

и устойчивость.

Треугольник –один из миниатюрных инструментов симфонического оркестра

Флористика

Французский высокий треугольник

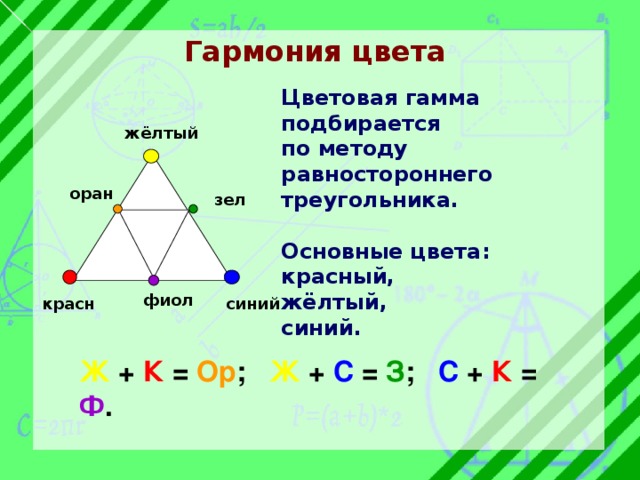
Гармония цвета

Цветовая гамма подбирается

по методу равностороннего

треугольника.

Основные цвета:

красный,

жёлтый,

синий.

жёлтый

оран

зел

фиол

синий

красн

Ж + К = Ор ; Ж + С = З ; С + К = Ф .

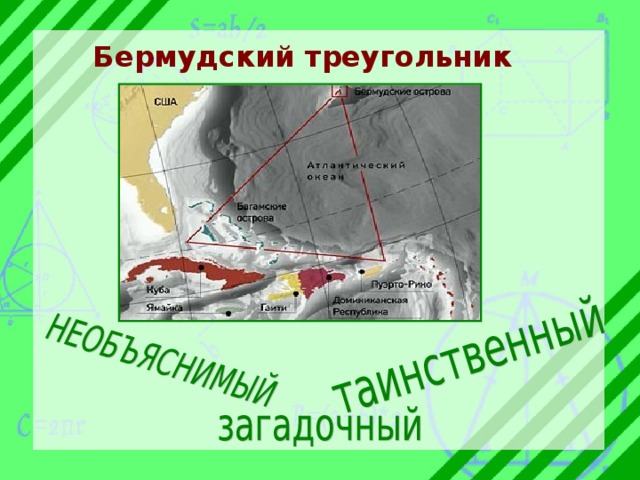
Бермудский треугольник

Треугольный дизайн

Треугольное оригами