Презентация по информатике "Сумматор двоичных чисел"

Презентация содержит девять слайдов.

И в двоичной системе счисления, и в алгебре  логики информация представлена в виде двоичных кодов (0,1).

Для того, чтобы максимально упростить работу компьютера, все математические операции сводятся к операции сложения. Поэтому главной частью процессора является сумматор, который как раз и обеспечивает такое сложение.

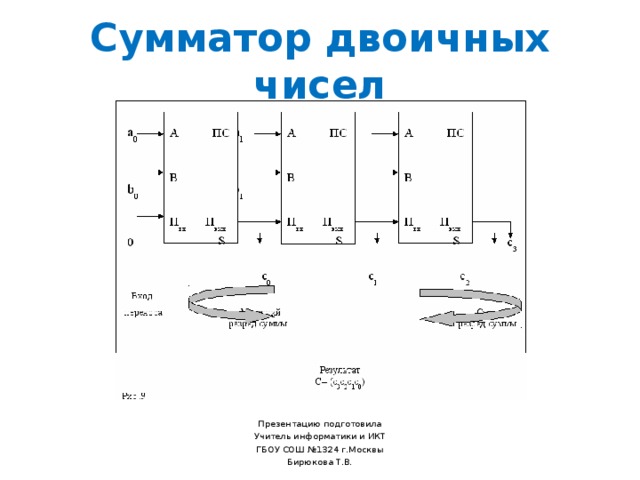
Сумматор двоичных чисел

Презентацию подготовила

Учитель информатики и ИКТ

ГБОУ СОШ №1324 г.Москвы

Бирюкова Т.В.

Сумматор двоичных чисел

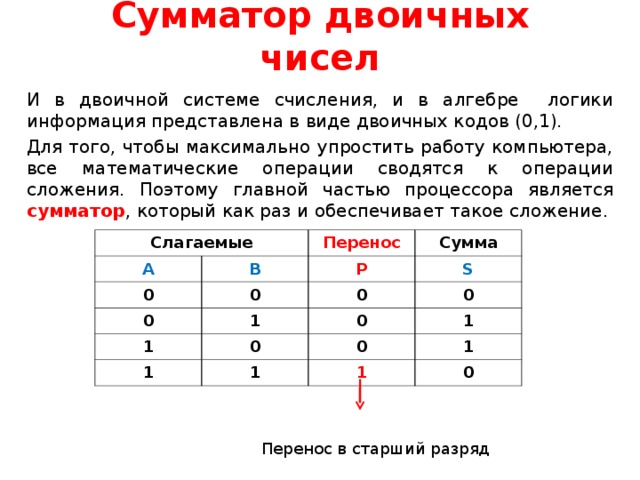
И в двоичной системе счисления, и в алгебре логики информация представлена в виде двоичных кодов (0,1).

Для того, чтобы максимально упростить работу компьютера, все математические операции сводятся к операции сложения. Поэтому главной частью процессора является сумматор , который как раз и обеспечивает такое сложение.

Слагаемые

А

Перенос

0

В

0

Сумма

P

0

1

1

0

S

0

0

0

1

1

0

1

1

1

0

Перенос в старший разряд

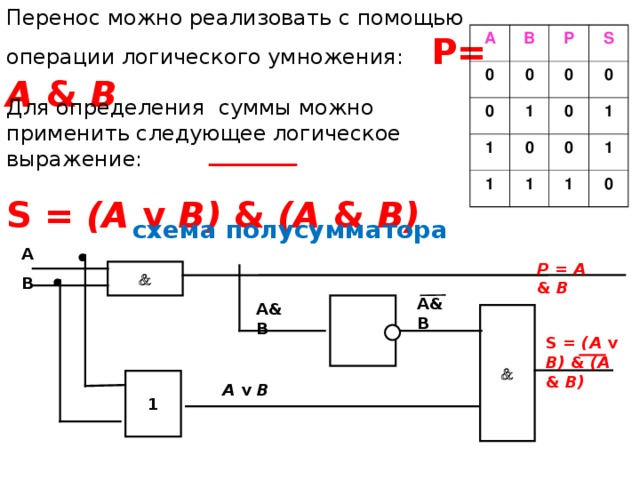
Перенос можно реализовать с помощью операции логического умножения: P = А & В

А

0

В

0

0

Р

1

0

1

S

0

1

0

0

1

1

0

1

1

0

Для определения суммы можно применить следующее логическое выражение:

S = (А v В) & (А & В)

схема полусумматора

А

В

P = А & В



A&B

A&B



S = (А v В) & (А & В)

1

А v В

Данная схема называется полусумматором , так как реализует суммирование одноразрядных двоичных чисел без учёта переноса из младшего разряда

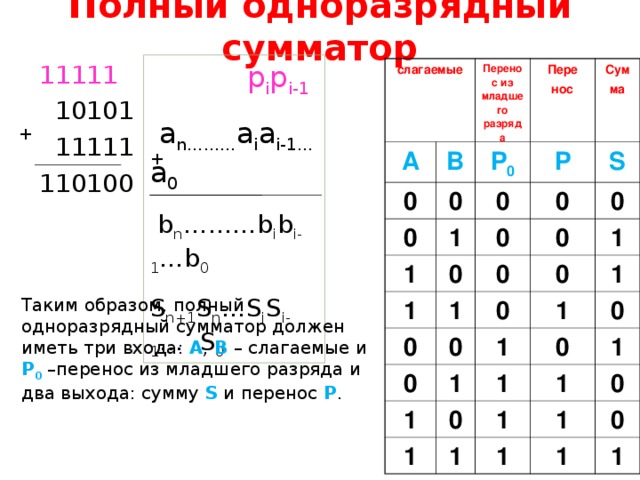
Полный одноразрядный сумматор

p i p i-1

a n……… a i a i-1… a 0

b n ………b i b i-1 …b 0

S n+1 S n …S i S i-1 … S 0

11111

10101

11111

110100

слагаемые

A

B

Перенос из младшего разряда

0

Пере

нос

0

0

P 0

1

1

0

P

Сум

ма

S

0

0

0

1

0

0

0

1

0

0

1

0

0

0

1

1

1

1

1

0

1

0

1

0

1

1

1

1

0

1

1

0

1

1

+

+

Таким образом, полный одноразрядный сумматор должен иметь три входа: А , В – слагаемые и P 0 – перенос из младшего разряда и два выхода: сумму S и перенос P .

слагаемые

A

Перенос из младшего разряда

0

B

Пере

нос

0

P 0

0

Сум

ма

0

1

P

1

1

0

0

0

S

0

0

0

1

0

0

0

0

1

0

1

1

1

1

1

0

1

1

0

0

1

1

1

1

0

1

1

1

0

1

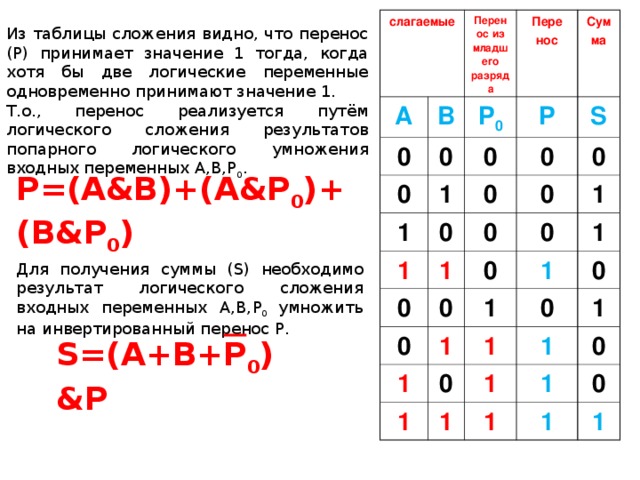
Из таблицы сложения видно, что перенос ( P ) принимает значение 1 тогда, когда хотя бы две логические переменные одновременно принимают значение 1.

Т.о., перенос реализуется путём логического сложения результатов попарного логического умножения входных переменных А,В, P 0 .

P=(A&B)+(A&P 0 )+(B&P 0 )

Для получения суммы ( S ) необходимо результат логического сложения входных переменных А,В, P 0 умножить на инвертированный перенос P .

S=(A+B+P 0 )&P

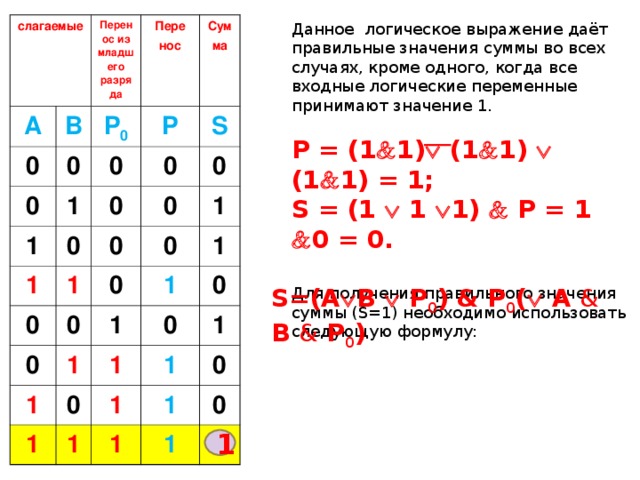
Данное логическое выражение даёт правильные значения суммы во всех случаях, кроме одного, когда все входные логические переменные принимают значение 1.

P = (1  1)  (1  1)  (1  1) = 1 ;

S = (1  1  1)  P = 1  0 = 0.

Для получения правильного значения суммы ( S=1 ) необходимо использовать следующую формулу:

слагаемые

A

B

Перенос из младшего разряда

0

0

0

Пере

нос

P 0

P

1

Сум

ма

1

0

1

0

S

0

0

0

1

0

0

0

0

0

1

0

0

1

1

1

1

1

1

0

0

0

1

1

1

1

1

1

1

0

0

1

1

S=(A  B  P 0 ) & P 0 (  A & B & P 0 )

1

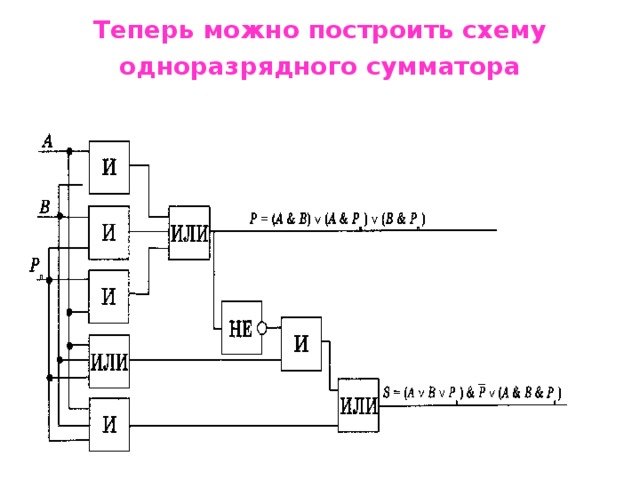
Теперь можно построить схему

одноразрядного сумматора

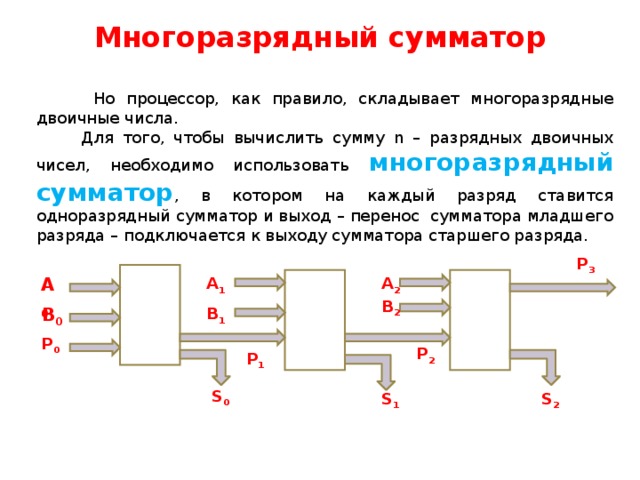
Многоразрядный сумматор

Но процессор, как правило, складывает многоразрядные двоичные числа.

Для того, чтобы вычислить сумму n – разрядных двоичных чисел, необходимо использовать многоразрядный сумматор , в котором на каждый разряд ставится одноразрядный сумматор и выход – перенос сумматора младшего разряда – подключается к выходу сумматора старшего разряда.

P 3

A 2

А 1

А 0

B 2

В 1

В 0

P 0

P 2

P 1

S 0

S 1

S 2