
«…нет ни одной области в математике, которая когда-либо не окажется применимой к явлениям действительного мира…»
Н.И. Лобачевский

Гипотеза:

Найдите производные функций:

Найдите производные функций:

Найдите производные функций:

Вопросы
1 ) Как связан “знак” производной с возрастанием и убыванием функции ?
2) Что называется точкой максимума?
3) Что называется точкой минимума?
4) Какие точки называются стационарными?
5) Какие точки называются критическими?
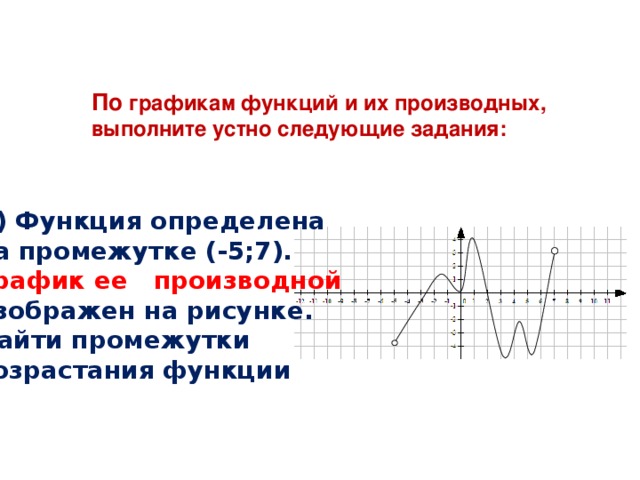
По графикам функций и их производных, выполните устно следующие задания:
А) Функция определена
на промежутке (-5;7).
График ее производной
изображен на рисунке.
Найти промежутки
возрастания функции
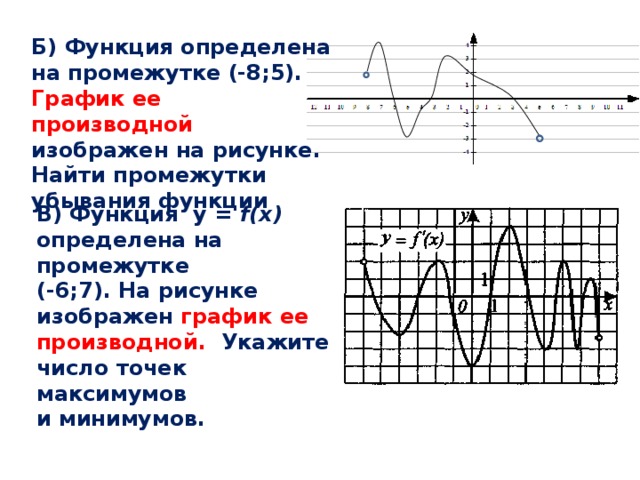
Б) Функция определена
на промежутке (-8;5).
График ее производной
изображен на рисунке.
Найти промежутки
убывания функции
В) Функция y = f(x) определена на промежутке
(-6;7). На рисунке изображен график ее
производной. Укажите число точек максимумов
и минимумов.
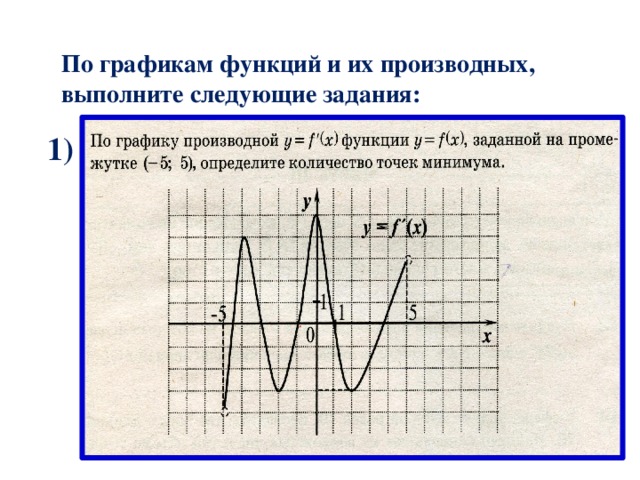
По графикам функций и их производных, выполните следующие задания:
1)
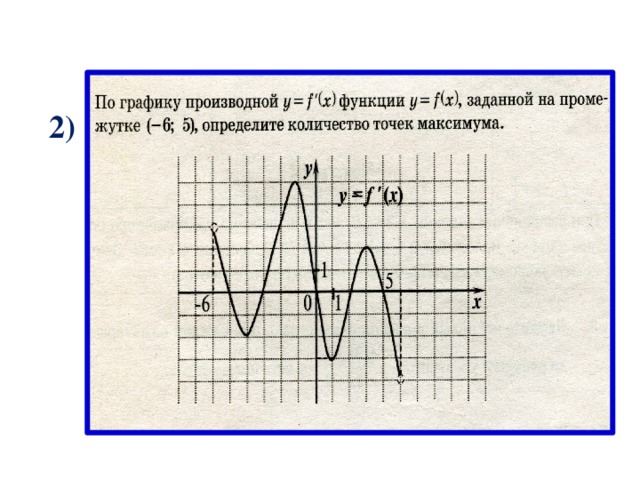
2)
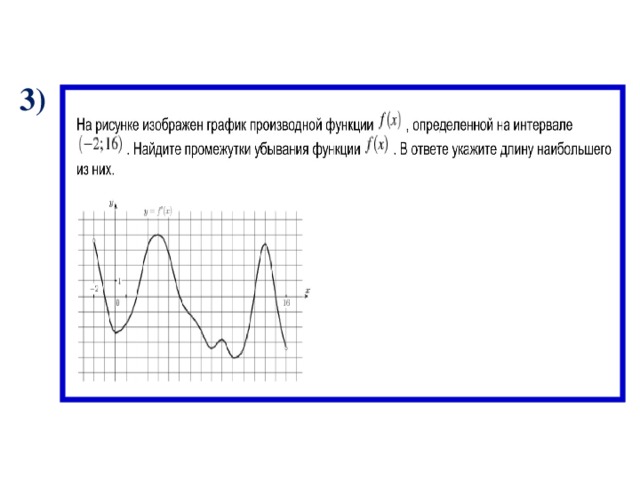
3)
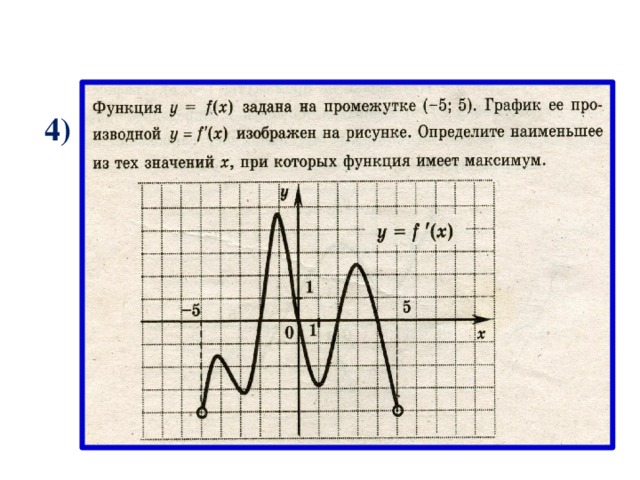
4)
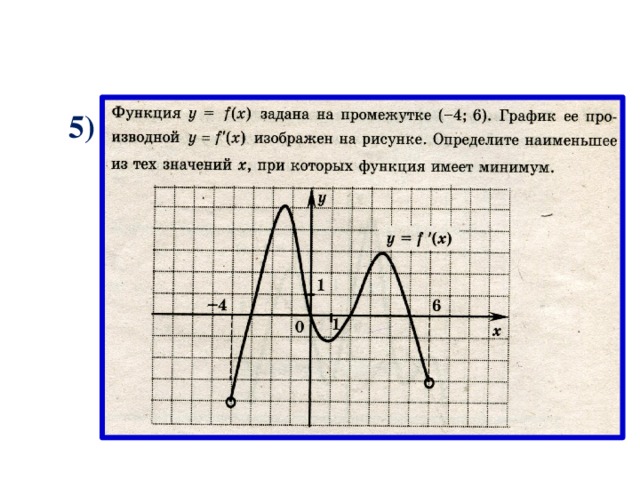
5)
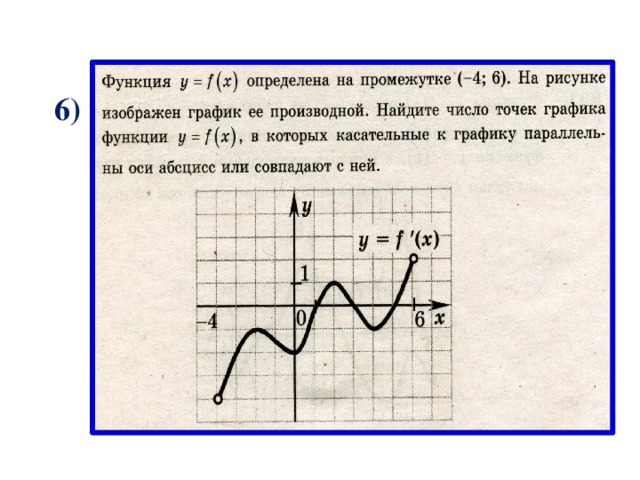
6)
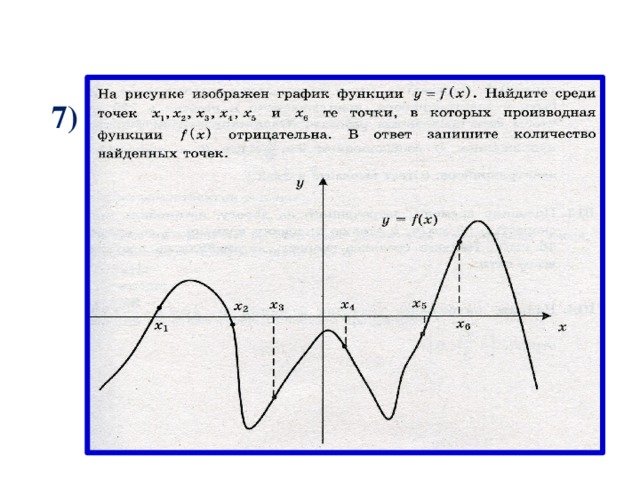
7)
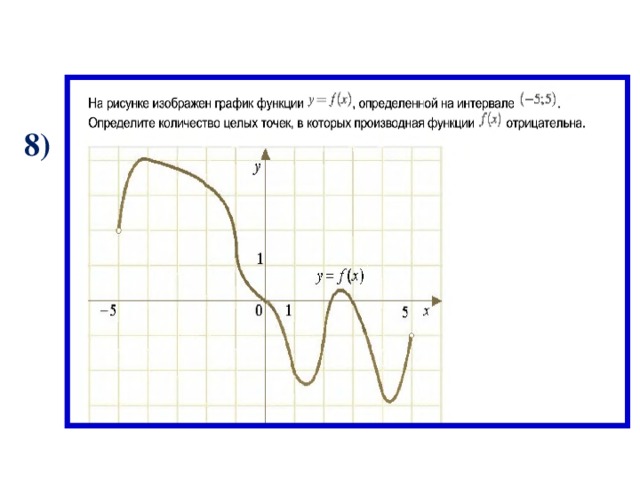
8)
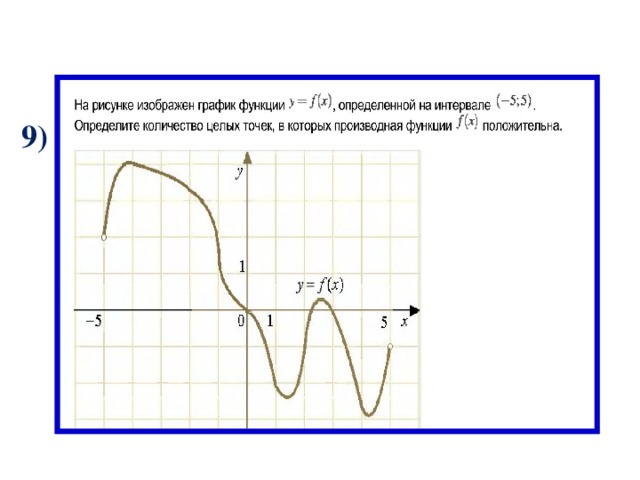
9)
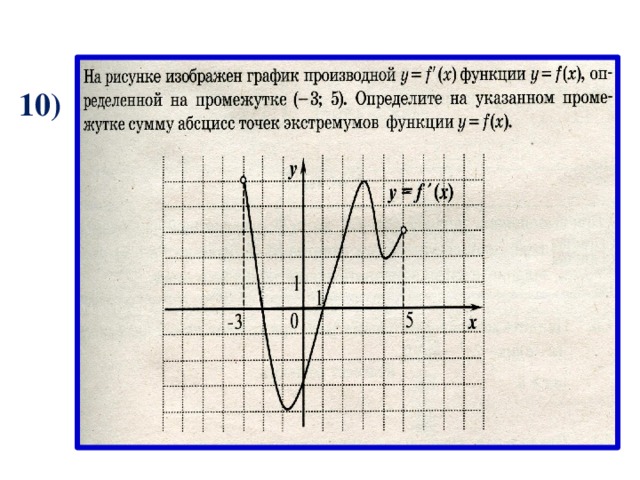
10)
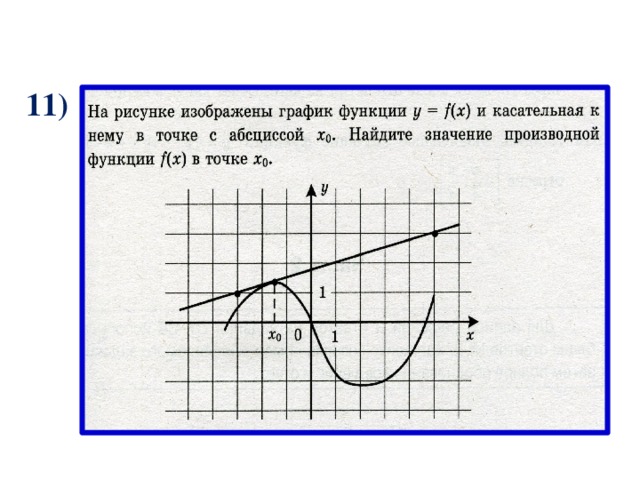
11)
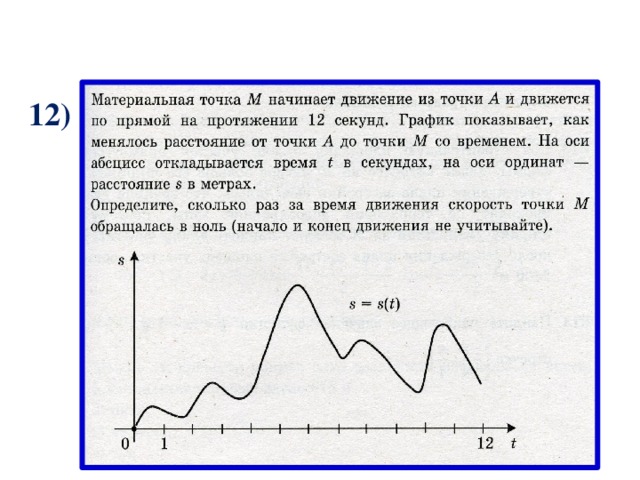
12)
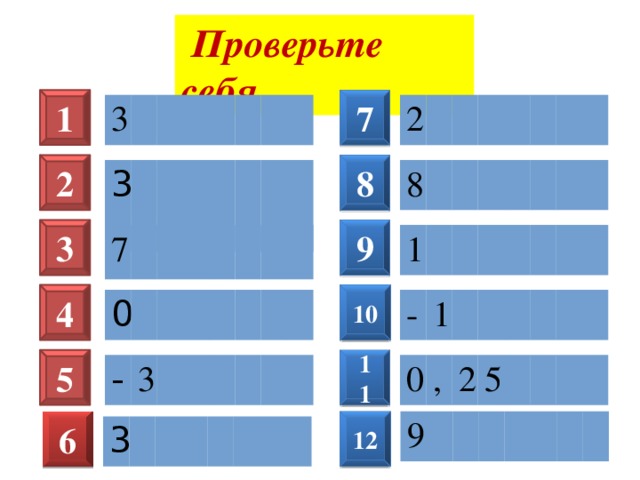
Проверьте себя
1
7
3
2
8
2
8
3
3
9
7
1
4
10
0
-
1
11 1
5
0
-
3
,
2
5
6
12
9
3

Найти угловой коэффициент касательной, проведенной к графику функции в точке с абсциссой x 0 .
Каждому верному ответу соответствует буква,
из этих букв необходимо составить имя известного математика.
1
-2
г
а
4
-1
л
а
2
3
и
н
5
-4
б
й
0
6
ж
р
8
7
е
ц

Из истории дифференциального исчисления
В 1638 году Ферма поделился этим открытием со своим земляком Рене Декартом, который также занимался этой проблемой и нашел свой метод построения касательных к алгебраическим кривым.
Ферма далеко продвинулся в применении дифференциальных методов, он использовал их не только для проведения касательных, но, к примеру, для нахождения максимумов, вычисления площадей. Однако ни Ферма, ни Декарт не сумели свести полученные научные выводы и результаты в единую систему.
- Великий французский математик Пьер Ферма в 1629 году научился находить касательные к алгебраическим кривым.

Из истории дифференциального исчисления
Тем не менее, выдвинутые идеи не пропали впустую .
Вильгельм
Лейбниц
(1646-1716)
Исаак
Ньютон
(1642-1727)
Многие из них легли в основу нового метода математического анализа – дифференциального исчисления, основоположниками которого считаются Вильям Лейбниц и Исаак Ньютон.

Из истории дифференциального исчисления Производная в математике показывает числовое выражение степени изменений величины, находящейся в одной и тоже точке, под влиянием различных условий. Формула производной встречается нам ещё в 15 веке. Великий итальянский математик Тартальи, рассматривая и развивая вопрос - на сколько зависит дальность полёта снаряда от наклона орудия - применяет её в своих трудах. Формула производной часто встречается в работах известных математиков 17 века. Посвящает целый трактат о роли производной в математике известный учёный Галилео Галилей. Затем производная и различные изложения с её применением стали встречаться в работах Декарта, французского математика Роберваля и англичанина Грегори. Большой вклад по изучению производной внесли такие умы, как Лопиталь, Бернулли, Лангранж и др.
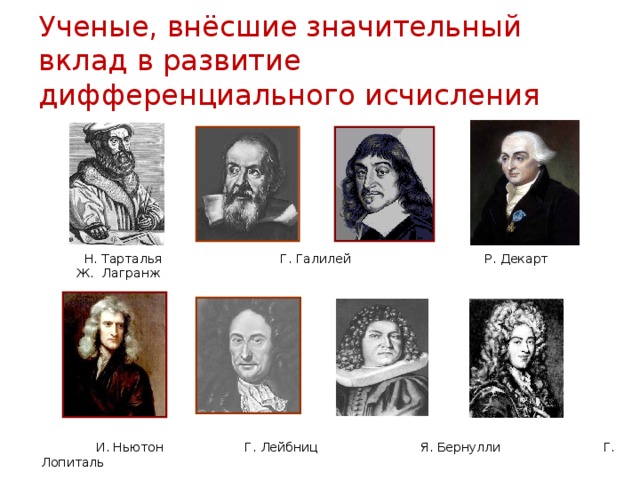
Ученые, внёсшие значительный вклад в развитие дифференциального исчисления
Н. Тарталья Г. Галилей Р. Декарт Ж. Лагранж
И. Ньютон Г. Лейбниц Я. Бернулли Г. Лопиталь

Исаак Ньютон (1642 – 1727)
И. Ньютон– великий английский физик, математик и астроном.
Автор фундаментального труда «Математические начала натуральной философии», в котором он описал закон всемирного тяготения и так называемые Законы Ньютона, заложившие основы классической механики.
Разработал дифференциальное и интегральное исчисление (автор знаменитого бинома Ньютона), теорию цветности и многие другие математически и физические теории .

Готфрид Фридрих Лейбниц (1646 – 1716)
Г. Лейбниц– немецкий философ, математик, физик, языковед.
Создал математический анализ – дифференциальное и интегральное исчисление, сформулировал основные понятия. В 1675 г четко указал на взаимно-обратный характер операций дифференцирования и интегрирования.
По просьбе Петра I разработал проекты развития образования и государственного управления в России.
Создал комбинаторику как науку.
Обосновал необходимость регулярно мерить у больных температуру тела.
Привел доказательства существования подсознания человека.

Жозеф Луи Лагранж (1736 – 1813)
Ж. Лагранж (25 января 1736 – 10 апреля 1813) – французский математик и механик итальянского происхождения, иностранный почетный член Петербургской АН (1776).
Лучший математик 18 века.
В 19 лет он стал профессором в Артиллерийской школе Турина. Именно Лагранж в 1791 г. ввёл термин «производная», ему же мы обязаны и современным обозначением производной (с помощью штриха). Термин «вторая производная» и обозначение(два штриха) также ввёл Лагранж

Применение производной в физике
- Если материальная точка движется прямолинейно и ее координата изменяется по закону x(t), то скорость ее движения v(t) в момент времени t равна производной т.е. производная от координаты по времени есть скорость
Производная от скорости по времени есть ускорение:
Ускорение движения есть скорость изменения скорости, поэтому ускорение движения в момент времени t равно производной Таким образом, ускорение движения в момент времени t равно т.е. равно производной от производной. Эту производную называют второй производной от функции и обозначают Итак,

Физический смысл
скорость
ускорение

Где ещё находит свое применение производная в физике?
- Если V(p) – закон изменения объема жидкости от внешнего давления p , то производная есть мгновенная скорость изменения объема при внешнем давлении, равном p .
- Сила есть производная работы по перемещению, т.е.
- Теплоемкость – есть производная теплоты по температуре, т.е.

Задача №1
Скорость школьного автобуса массой 5 т возрастает по закону υ = 0,1 t 3 + 0,2 t .
Определить равнодействующую всех сил, действующих на него в момент времени 2 с.
Решение

Задача №2
- Две материальные точки движутся прямолинейно по законам
В какой момент времени скорости их равны, т.е.
Решение

Задача №3
Точка движется прямолинейно по закону
Вычислите скорость движения точки:
а) в момент времени t;
б) в момент времени t=2с.
Решение.
а)
б)

Задача №4
Найдите скорость и ускорение для точки, движущейся по закону
а) в момент времени t;
б) в момент времени t=3с.
Решение.

Применение производной в химии и биологии
И в химии нашло широкое применение дифференциальное исчисление для построения математических моделей химических реакций и последующего описания их свойств. Химия – это наука о веществах, о химических превращениях веществ. Химия изучает закономерности протекания различных реакций
Определение скорости
химической реакции
Скоростью химической реакции называется изменение концентрации реагирующих веществ в единицу времени.

Зачем нужна производная в реакциях ?
Так как скорость реакции v непрерывно изменяется в ходе процесса, ее обычно выражают производной концентрации реагирующих веществ по времени.

Формула производной в химии
Если C(t) – закон изменения количества вещества, вступившего в химическую реакцию, то скорость v(t) химической реакции в момент времени t равна производной:

Определение скорости реакции
Предел отношения приращённой функции к приращённому аргументу при стремлении Δt к нулю - есть скорость химической реакции в данный момент времени

Задача по химии:
Пусть количество вещества, вступившего в химическую реакцию задается зависимостью:
С(t) = t 2 /2 + 3t –3 (моль)
Найти скорость химической реакции через 3 секунды.
Решение:
v (t) = С ‘(t);
v (t) = t + 3;
v (3) = 3+3 = 6.
Ответ: 6 моль\с.

Биологический смысл производной
Пусть зависимость между числом особей популяции микроорганизмов у и временем t её размножения задана уравнением: у = x(t). Пусть ∆t - промежуток времени от некоторого начального значения t до t+∆t. Тогда у + ∆у = x(t+∆t) - новое значение численности популяции, соответствующее моменту t+∆t , а ∆y + x(t + ∆t )- x(t) - изменение числа особей организмов. Отношение является средней скоростью размножения или, как принято говорить, средней производительностью жизнедеятельности популяции. Вычисляя , получаем y ‘ = P(t) = x ‘ (t) , или производительность жизнедеятельности популяции в момент времени t .

Популяция – это совокупность особей данного вида, занимающих определённый участок территории внутри ареала вида, свободно скрещивающихся между собой и частично или полностью изолированных от других популяций, а также является элементарной единицей эволюции.
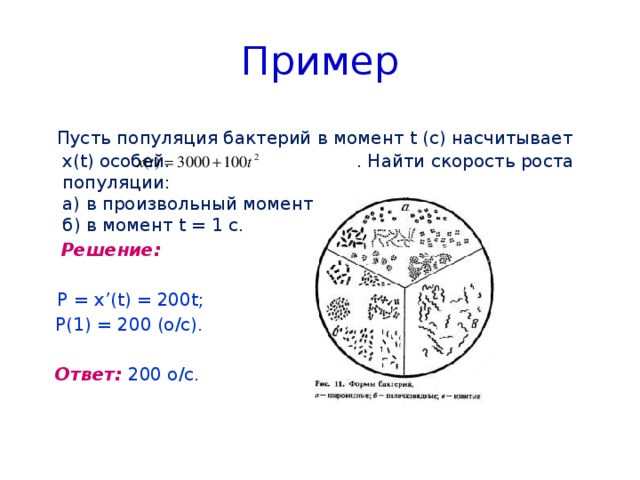
Пример
Пусть популяция бактерий в момент t (с) насчитывает x(t) особей. . Найти скорость роста популяции: а) в произвольный момент t, б) в момент t = 1 c.
Решение:
P = x’(t) = 200t;
P(1) = 200 (о/с).
Ответ: 200 о/с.

Заключение
Понятие производной очень важно в химии и в биологии, особенно при определении скорости течения реакции.

Применение производной в географии
Производная помогает рассчитать:
- Некоторые значения в сейсмографии
- Особенности электромагнитного поля земли
- Радиоактивность
ядерно-геофизических
показателей
в экономической географии

ЭТО Я
ЭТО Я
ЭТО Я
ЭТО Я
ЭТО Я
Численность населения
Идея социологической модели Томаса Мальтуса состоит в том, что прирост населения пропорционален числу населения в данный момент времени t. Модель Мальтуса неплохо действовала для описания численности населения
США с 1790 по 1860 годы.
Ныне эта модель
в большинстве стран
не действует.
47

Пример
Вывести формулу для вычисления численности населения на ограниченной территории в момент времени t.
РЕШЕНИЕ:
Пусть у=у(t)- численность населения.
Рассмотрим прирост населения за t=t-t 0
y=k y t, где к=к р – к с –коэффициент прироста
(к р – коэффициент рождаемости,
к с – коэффициент смертности)
y/ t=k y
При t 0 получим lim y/ t=у’
у’=к у
47

Применение производной в экономике
- Экономика — хозяйственная деятельность общества, а также совокупность отношений, складывающихся в системе производства, распределения, обмена и потребления.

Решение задач
П (t) = υ / (t) - производительность труда,
где υ (t) - объем продукции
J(x) = y / (x) - предельные издержки производства,
где y– издержки производства в зависимости от объема выпускаемой продукции x.

Задача
Оборот предприятия за истекший год описывается через функцию U(t)=0,15t³ – 2t² + 200, где t – месяцы, U-миллионы.
Исследуйте оборот предприятия за 9 и 10 месяцы.
Решение: Исследуем оборот предприятия с помощью производной: U'(t)=0,45t² - 4t
Меньший оборот был на девятом месяце- 0,45. На 10 месяце -5.

Вывод:
Дифференциальное исчисление- это описание окружающего нас мира, выполненное на математическом языке. Производная - одно из самых важных понятий математического анализа. Знание производной помогает нам успешно решать не только математические задачи, но и задачи практического характера в разных областях науки, техники и жизни.
![ПРИМЕР 1 1)Найти наибольшее и наименьшее значение функции y=x 2 - 8x+19 на [-1;5]](https://fsd.videouroki.net/html/2014/09/04/98685854/img52.jpg)
ПРИМЕР 1
1)Найти наибольшее и наименьшее значение функции y=x 2 - 8x+19 на [-1;5]
![РЕШЕНИЕ 1)Найти наибольшее и наименьшее значение функции y=x 2 - 8x+19 на [-1;5] 1) 2) 2x+8=0 2x=-8 x=-4 3) 4)](https://fsd.videouroki.net/html/2014/09/04/98685854/img53.jpg)
РЕШЕНИЕ
1)Найти наибольшее и наименьшее значение функции y=x 2 - 8x+19 на [-1;5]
1)
2) 2x+8=0
2x=-8
x=-4
3)
4)

Выбери картинку, соответствующую твоему настроению на уроке:
Урок окончен. Спасибо за работу


 Получите свидетельство
Получите свидетельство Вход
Вход























































![ПРИМЕР 1 1)Найти наибольшее и наименьшее значение функции y=x 2 - 8x+19 на [-1;5]](https://fsd.videouroki.net/html/2014/09/04/98685854/img52.jpg)
![РЕШЕНИЕ 1)Найти наибольшее и наименьшее значение функции y=x 2 - 8x+19 на [-1;5] 1) 2) 2x+8=0 2x=-8 x=-4 3) 4)](https://fsd.videouroki.net/html/2014/09/04/98685854/img53.jpg)










 Презентация по алгебре "Применение производной" (5.61 MB)
Презентация по алгебре "Применение производной" (5.61 MB)
 0
0 1171
1171 63
63 Нравится
0
Нравится
0


