Презентация по алгебре на тему "Квадратичная функция"

Функция у=кх², где коэффициент к- любое отличное от нуля число, рассматривается остенсивно, т.е. через пример.

Функцию у=f(x) называют ограниченной сверху, если все значения функции меньше некоторого числа. Геометрически это означает, что график функции расположен ниже некоторой прямой, параллельной  оси х.

Постройте график функции у=х²

Что является графиком данной функции?( парабола).

Постройте график функции у=2х²

Что является графиком данной функции?

( парабола).

Постройте график функции у=0,5х²

Что является графиком данной функции?

( парабола).

Что общего у трех данных функций? (х²)

Чем отличаются 2 последние функции от 1? ( в последних 2 перед  х² стоят числа)

Так вот ребята такие функции мы будем называть квадратичными.

В виде формулы квадратичная функция выглядит  следующим образом: у=кх², где к- любое отличное от нуля число.

Квадратичная функция

§9 Функция у=кх², ее свойства и график

Как такового определения понятию « Квадратичная функция» не дается.

Функция у=кх², где коэффициент к- любое отличное от нуля число, рассматривается остенсивно, т.е. через пример.

Формирование новых знаний

• Постройте график функции у=х²

• Что является графиком данной функции?( парабола).

у

у=х²

0

х

Формирование новых знаний

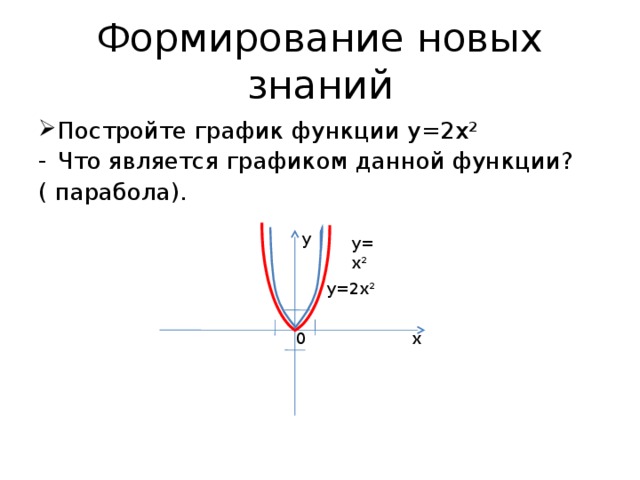
• Постройте график функции у=2х²

• Что является графиком данной функции?

( парабола).

у

у=х²

у=2х²

0

х

Формирование новых знаний

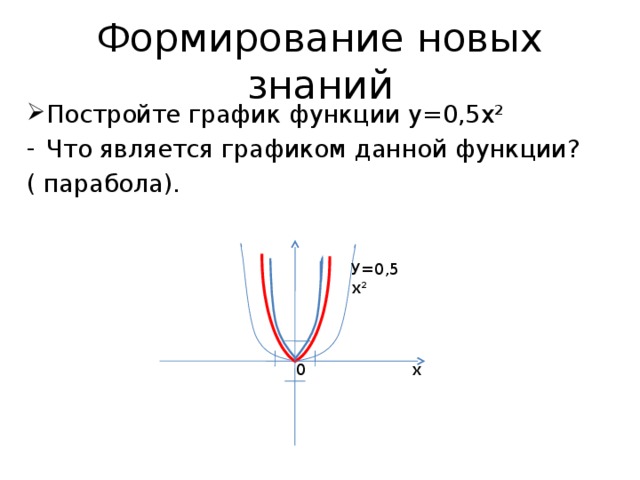
• Постройте график функции у=0,5х²

• Что является графиком данной функции?

( парабола).

У=0,5х²

х

0

• Что общего у трех данных функций? (х²)
• Чем отличаются 2 последние функции

от 1? ( в последних 2 перед х² стоят числа)

Так вот ребята такие функции мы будем называть квадратичными.

• В виде формулы квадратичная функция выглядит следующим образом:

у=кх², где к- любое отличное от нуля число.

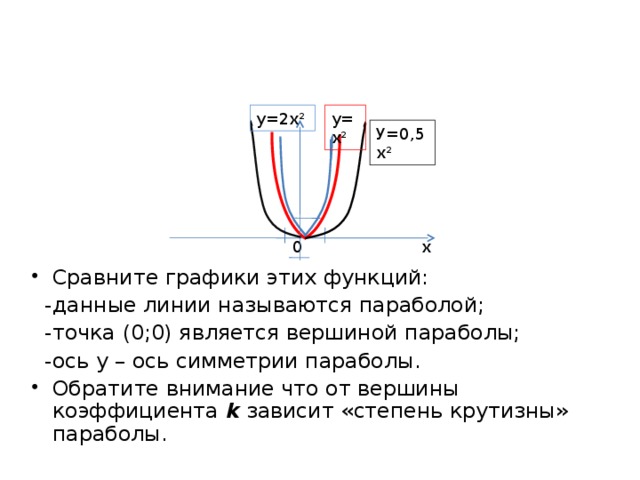
у=2х²

у=х²

У=0,5х²

х

0

• Сравните графики этих функций:

-данные линии называются параболой;

-точка (0;0) является вершиной параболы;

-ось у – ось симметрии параболы.

• Обратите внимание что от вершины коэффициента k зависит «степень крутизны» параболы.

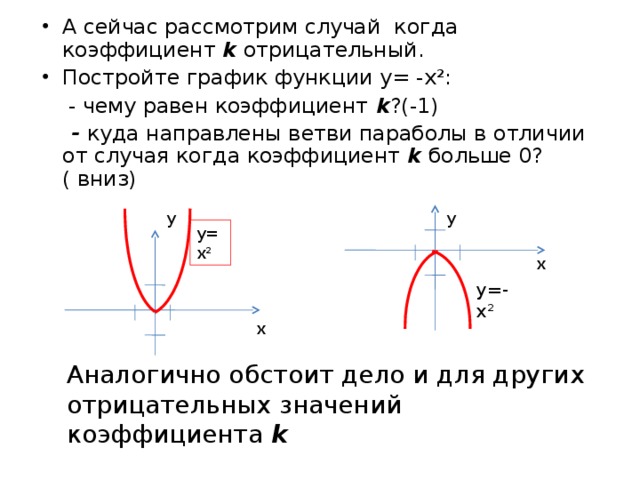
• А сейчас рассмотрим случай когда коэффициент k отрицательный.
• Постройте график функции у= -х²:

- чему равен коэффициент k ?(-1)

- куда направлены ветви параболы в отличии от случая когда коэффициент k больше 0?( вниз)

у

у

у=х²

х

у=-х²

х

Аналогично обстоит дело и для других отрицательных значений коэффициента k

0 и вниз при к " width="640"

• Графиком функции у= кх²( к≠0) является парабола с вершиной в начале координат; ось у является осью параболы; ветви параболы направлены вверх при к0 и вниз при к

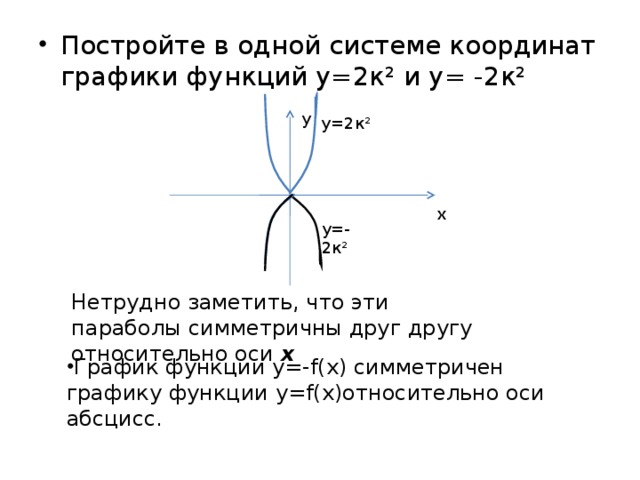
• Постройте в одной системе координат графики функций у=2к² и у= -2к²

у

у=2к²

х

у=-2к²

Нетрудно заметить, что эти параболы симметричны друг другу относительно оси х

• График функции у=- f(x) симметричен графику функции у= f(x) относительно оси абсцисс.

0 Описывая свойства этой функции, будем опираться на ее геометрическую модель- параболу. у у=кх²(к0) х у=-1 " width="640"

Свойства функций у=кх² при к0

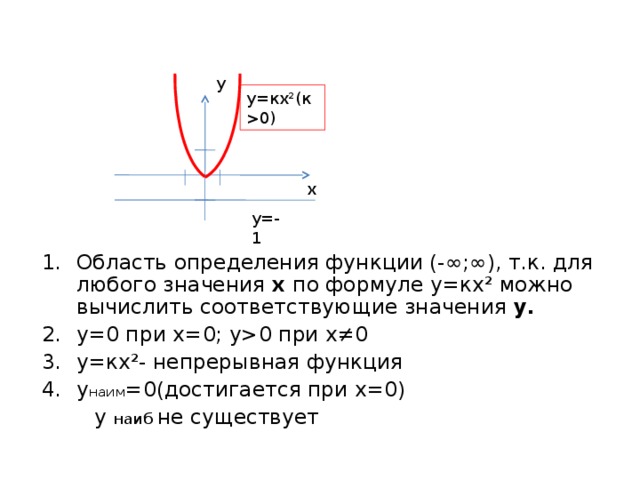
Описывая свойства этой функции, будем опираться на ее геометрическую модель- параболу.

у

у=кх²(к0)

х

у=-1

0) х у=-1 Область определения функции (-∞;∞), т.к. для любого значения х по формуле у=кх² можно вычислить соответствующие значения у. у=0 при х=0; у0 при х≠0 у=кх²- непрерывная функция у наим =0(достигается при х=0) у наиб не существует " width="640"

у

у=кх²(к0)

х

у=-1

• Область определения функции (-∞;∞), т.к. для любого значения х по формуле у=кх² можно вычислить соответствующие значения у.
• у=0 при х=0; у0 при х≠0
• у=кх²- непрерывная функция
• у наим =0(достигается при х=0)

у наиб не существует

• Функцию у= f(x) называют ограниченной снизу, если все значения функции больше некоторого числа. Геометрически это означает, что график функции расположен выше некоторой прямой, параллельной оси х.
• Функцию у= f(x) называют ограниченной сверху, если все значения функции меньше некоторого числа. Геометрически это означает, что график функции расположен ниже некоторой прямой, параллельной оси х.

0) х у=-1 5. Функция у=кх²(к0) ограничена снизу и не ограничена сверху. " width="640"

у

у=кх²(к0)

х

у=-1

5. Функция у=кх²(к0) ограничена снизу и не ограничена сверху.

Свойства функции у=кх² при к

у=1

х

у=кх²(к

у

• Область определения функции (-∞;∞)
• У=0 при х = 0; у
• У=кх² - непрерывная функция.
• у наиб = 0(достигается при х=0).

у наим не существует.

5.Функция ограничена сверху и не ограничена снизу.